BP神经网络PID在扭矩标准机上的建模与实现
刘健东
(广州计量检测技术研究院,广东 广州 510663)
0 引言
静重式扭矩标准机是进行扭矩量值传递的基础。其采用砝码的力源作为标准力值,借助力臂杠杆的相互作用形成标准扭矩,直接或经过特定的杠杆机械结构产生标准扭矩,并施加到被检对象上[1]。在扭矩计量方面,在国际上具有权威性的是德国物理技术研究院(Physikalisch-Technische Bundesanstalt,PTB)。很多国家的扭矩标准装置结构基本参照PTB的标准装置进行设计[2]。目前处于国内领先水平的一级扭矩计量站,其装置的加载方式均为分段式速度加载[3]。在检定扭矩传感器过程中,连接往往存在不同大小的间隙。各品牌扭矩传感器材料弹性模量各不相同,如依旧使用传统的控制逻辑,会导致检定校准过程单一、缓慢。同时,依据目前现行的国家检定规程操作,在实际使用中检定校准过程往往需要花费大量时间[4]。
由于组态软件与可编程逻辑控制器(programmable logic controller,PLC)控制系统自身技术的局限,使用其内部数据库与程序,难以引入先进的控制算法。针对扭矩标准机加载系统中用于平衡加载砝码的二相混合式步进电机,本文提出了基于误差反向传播(back propagation,BP)神经网络自适应比例积分微分(proportional integral differential,PID)控制系统算法。该控制算法使用用于过程控制的对象连接与嵌入(object linking and embedding for process control,OPC)通信协议实现组态王与Matlab的数据交换,将组态软件与神经网络自适应PID控制算法相结合。经过PLC编程后的静态扭矩标准机实现了智能化自整定、自适应的功能。该项技术可以使扭矩标准机在不同安装状况、不同被测对象中依旧平稳加载至目标值,从而大幅度缩小各级扭矩加载时间。
1 加载控制系统建模
本文以实验室中的一台3 000 Nm静重式扭矩标准机为研究对象。加载系统由PLC控制器以及上位机、标准力臂机构、力臂平衡机构、砝码加载机构、位移传感器组成。该自动控制系统的控制对象为平衡杠杆上的位移传感器相对位置,而被控对象为混合式两相伺服电机输出。所以该系统是一个典型单闭环伺服系统。伺服系统PID控制如图1所示。

图1 伺服系统PID控制框图Fig.1 PID control block diagram of servo system
系统中,输入量环节受到扭矩传感器安装间隙与受力形变因素影响,在安装不同的被检传感器时往往引入不同的时滞和非线性高阶项,导致整个控制系统不确定因素增加,影响系统稳定性。现代控制系统理论建模中,将输入作为扰动信号并简化为单位脉冲信号,以便后续反馈系统建模设计分析。
在步进电机的控制中,需要在负载扭矩中进行高分辨率步进角度控制,同时减缓运转过程的震动和噪声,以提高转角精度和运行平稳性。因此,需要利用步进电机驱动器对其进行细分驱动[5]。本文选用的是KINCO 2S110Q-03999两相式步进电机,其步进角θb为1.8°,搭配2H1160步进电机驱动器,可用于细分控制。驱动器顶部设置八段双列直插封装(dual in-line package,DIP),设定开关中的DIP2、DIP3、DIP4为OFF、OFF、OFF,并选择128步细分驱动控制。步进角结合细分控制步进电机的转角θ为:
式中:P为脉冲数;n为细分数。
减速机是负责传递动能的机械结构,利用不同齿数的齿轮啮合构成速度转换器,使高速运转动力装置的速度变为正常工作所需要的速度。减速机能有效提高转矩的输出,同时可减少负载惯量。在此采用大型减速机,减速比i为5 294.8。其输出转速ω为:
式中:ω0为输入转速;i为转速比。
控制角度可由转速随时间积分得到。
非接触式位移传感器安装于平衡杠杆的特定位置,距离杠杆中心支点为固定距离,即0.665 m。
D=L×sinθL
(3)
式中:D为位移传感器读取的相对位移值;L为位移传感器平衡杠杆位置长度;θL为平衡杠杆偏移水平面角度。
经过传感器线性变换转换为采样信号d,由单位换算关系可得:
Δd=D×100 000
(4)
式中:Δd为经过传感器线性变换转换为采样模拟量输入的变化值。
取杠杆平衡位置为采样信号的零点d0=0。根据d=d0+Δd,Δd的值为实际相对位移输出。
执行机构需要控制驱动步进电机的增量,采用经典增量式PID控制[6],利用闭环反馈原理,以系统输出值与期望值的差作为系统偏差,纠正控制输出值。其控制器逻辑可由式(5)实现。
式中:u(k)为本次控制量;u(k-1)为上次控制量;e(k)为本次偏差;rin(k)为系统期望值;yout(k)为控制对象输出实际值;e(k-1)为上次偏差;e(k-2)为上上次偏差;Kp为比例系数;Ki为积分系数;Kd为微分系数。
建立经典的增量式PID控制器之后,使用Simulink对系统进行数学建模。在Simulink建立PID控制框图如图2所示。
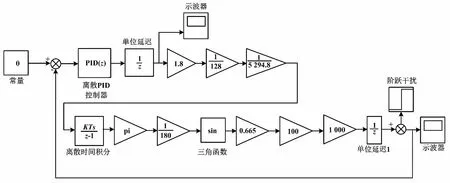
图2 在Simulink建立PID控制框图Fig.2 PID control block diagram in Simulink
闭环传递函数根据等效变换法则,可简化为:
式中:G(s)为连续系统闭环传递函数;s为拉氏变换的s域。
对闭环传递函数作离散Z变换,设置采样时间1 s,可得简化闭环传递函数为:
式中:G(z)为离散系统闭环传递函数;z为Z变换的z域。
在Simulink建立简化PID控制框图如图3所示。

图3 在Simulink建立简化PID控制框图Fig.3 Simplified PID control block diagram in Simulink
2 BP神经网络自适应PID控制系统
PID神经网络是一种新型的多层神经元网络,可作为系统的解耦控制器,由经典增量式PID控制器和BP神经网络算法组合而成。BP神经网络PID控制器结构如图4所示。其PID控制利用BP神经网络整定实时更新,具有良好的自学习和自适应解耦控制特性[7]。
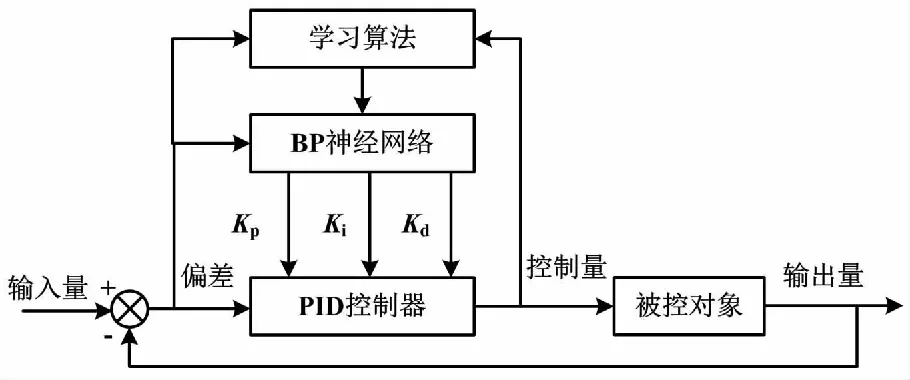
图4 BP神经网络PID控制器结构Fig.4 BP neural network PID controller structureBP
BP神经网络算法是基于生物神经网络,模拟人的形象思维和信息处理能力的算法,需要经历学习过程。实际使用时,需要大量数据,并通过学习不断更新连接权重,使得神经网络逐渐逼近非线性系统。
BP神经网络结构如图5所示。
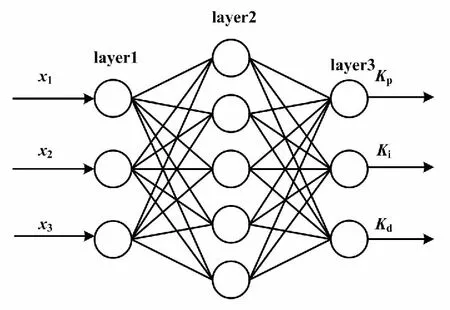
图5 BP神经网络结构Fig.5 BP neural network structureBP
BP神经网络利用输入前向传播、误差闭环反馈信号反向传播和梯度下降的基本原理[8],以链式求导法则获取权值更新变化规律,使权值可以按照一定的函数规律进行更新迭代[9];通过对权值的输出调节PID控制参数,达到降低误差、取代人工调节参数,并使神经网络输出对应于最优控制规律的PID控制参数的目的。由于不受制于被控对象,通过加入神经网络对PID控制进行参数自整定,能大幅度提高控制系统的鲁棒性。
BP神经网络控制器网络由输入层Layer1、隐含层Layer2、输出层Layer3三层结构组成。输入层的三个输入分别对应期望值x1、实际值x2、偏差x3。输出层的三个输出分别对应比例系数KP、积分系数Ki、微分系数Kd。隐含层共五层。BP神经网络的学习原理是反向梯度下降算法。
Simulink仿真设计由初始化与仿真循环两个部分组成。其中,仿真输出由求解器控制,负责传递模块输出、对状态量的积分求导和确定采样时间。系统的作用是计算模块输出、计算导数状态、计算状态更新、产生过零事件。在S函数中通过不同标志(flag)和子函数,控制求解器和系统之间的信息传递。BP神经网络PID控制器仿真结构如图6所示。
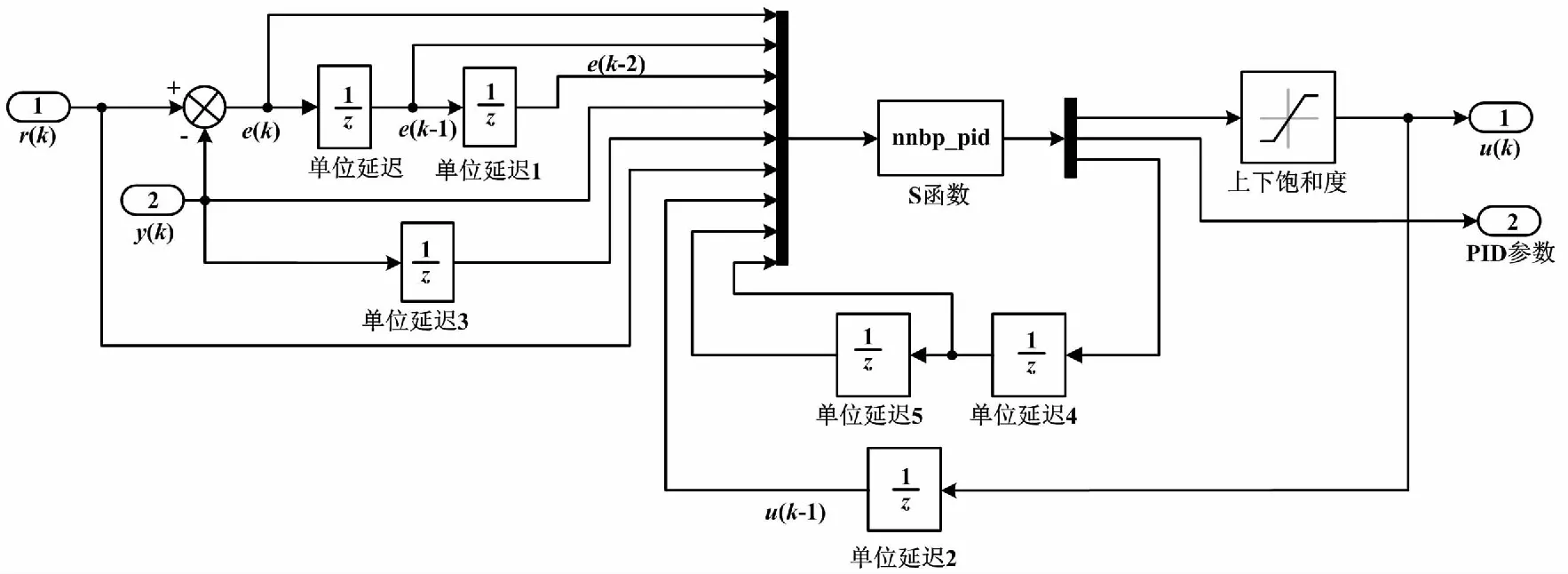
图6 BP神经网络PID控制器仿真结构图Fig.6 Simulation structure diagram of BP neural network PID controller
在图6中,BP神经网络控制器由S函数实现。S函数控制结构如图7所示。
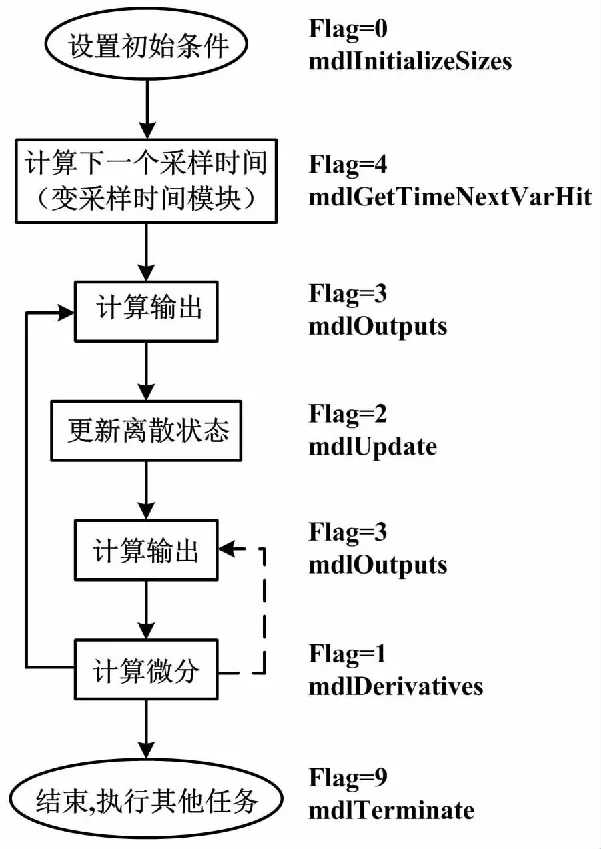
图7 S函数控制结构图Fig.7 S-function control structure diagramS
S函数初始化通过mdlInitializeSizes子函数,flag=0的方法实现。
BP神经网络控制函数由以下数学逻辑得出。
BP神经网络控制器的输入层输入量为:
oj(k)=uj,j=1,2,3
(8)
BP神经网络控制器隐含层的输入量和输出量分别为:
oi(k)=f[ni(k)],i=1,2,...,5
(10)
隐含层神经元采用双曲正切Sigmoid函数为激发函数:
BP神经网络控制器输出层的输入量和输出量分别为:
ol(k)=g[nl(k)],l=1,2,3
(13)
其中,输出层输出量为PID控制参数,即:
输出层神经元以tanh函数为激发函数:
通过学习率η、惯性因子α梯度下降法修正神经元加权系数,性能指标函数为:
根据PID控制计算方法,即式(5),可得:
(17)
BP神经网络输出层加权系数计算式为:
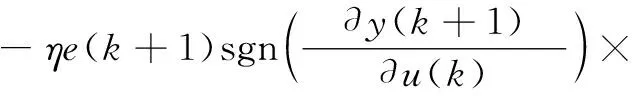
j=1,2,3,i=1,2,34,5l=1,2,3
(18)
BP神经网络PID调参功能主要通过S函数程序结构实现[10]。根据η、α梯度下降法修正神经元加权系数。在Simulink仿真中,PID控制由梯度下降设置相同的η和α。在使用Sigmoid函数作为激活函数时,固定的η、α会导致网络训练收敛速度比较缓慢。需要长时间多次收集庞大的训练数据,才能整定出最优整定系数。由于实际应用中学习方式为在线学习,无法像在仿真学习状态下得出庞大的训练数据。在线训练数据有限的条件下,输出PID控制参数时需要各自乘以不同的放大系数(放大系数由经验法人工整定得出)。增加放大系数后,该控制系统可以增大收敛速度、减少训练时间,并且不易产生振荡。
BP神经网络PID控制模型如图8所示。
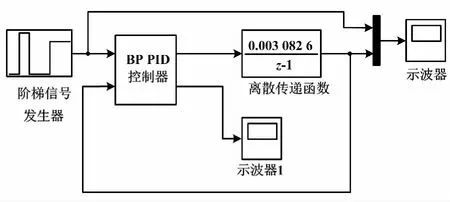
图8 BP神经网络PID控制模型Fig.8 PID control model of BP neural network
图8中:信号源为阶梯信号发生器;BP神经网络PID控制器参数可由双击S函数图标弹出对话框输入神经网络参数得到,包括η、α、隐含层数nh、输出动作值限制最大值Um、采样时间T、隐含层的激活函数与输出层的激活函数。如果η取值偏大,容易产生震荡; 取值偏小,收敛速度慢。这里选择合适的η=0.1,取常用的非线性Sigmoid函数作为隐含层输出层激活函数,把神经元连续输入值映射到0~1之间作为输出。BP神经网络PID控制阶跃信号、阶梯信号响应如图9所示。图9中:rin为阶跃阶梯输入信号函数;yout为阶跃阶梯信号响应函数。

图9 BP神经网络PID控制阶跃信号、阶梯信号响应Fig.9 BP neural network PID control step signal and step signal response
Ki、KP、Kd参数变化曲线如图10所示。
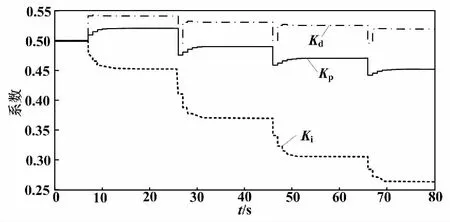
图10 Ki、KP、Kd参数变化曲线Fig.10 Ki,KP,Kd parameter change curves
由图9、图10可知,PID控制器的三个参数不再是固定的,而是随时间变化,因此可以很好地实现对控制对象的跟踪控制。这种控制策略可以实现较好的控制效果。
3 Matlab与组态王通信——OPC通信
本软件通过建立OPC服务器实现组态软件与Matlab相结合的控制。两者之间利用OPC的方法进行数据交换。OPC数据交换结构如图11所示。

图11 OPC数据交换结构图Fig.11 OPC data exchange structure diagram
OPC广泛应用于工业控制领域,由OPC 服务器和OPC 客户组成。OPC 服务器负责提供数据。OPC客户负责数据的处理。不同来源的数据都可以通过OPC服务器转发[11]。OPC服务器与OPC客户的连接可由OPC客户根据需求断开或连接。建立OPC服务器,可以实现Matlab、PLC和组态软件的数据交换。OPC数据存取服务器主要由Server、Group和Item这三类对象组成[12]。
根据OPC服务器,在组态软件建立OPC服务器KingView.View.1,并在服务器中建立各项数据项对象Item。
使用Matlab编写m文件,建立OPC服务器连接。建立的组态王组态软件界面中,PID控制可以通过OPC服务器与Matlab通信,实现在线PID控制自整定。实际PLC控制程序中,在PID控制逻辑稳定误差达到±4%,保持3 s后就会切断控制,达到平衡状态,供人员读取仪器数据。控制性能的优劣主要从平均超调量和平均上升时间两方面衡量。PID控制性能对比如表1所示。
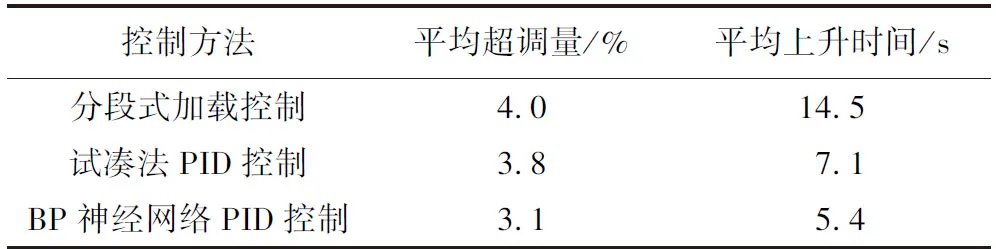
表1 PID控制性能对比Tab.1 Comparison of PID control performance
在实际应用中,试验对象选择型号为JN338的扭矩传感器,其量程为400~2 000 Nm。验证过程使用实验室0.05级、量程为3 000 Nm的静重式扭矩标准机对该扭矩传感器按照静态扭矩测量仪检定规程进行检定。根据国家检定规程,检定过程要求预载一次,再分别检定加载三次。在每次加载或卸载动作的间隔中,判断动作完成需要等待的时间为3 s。本次验证过程中,除去检定时人为读数与手写原始记录的时间。实际应用中的PID控制性能对比如表2所示。
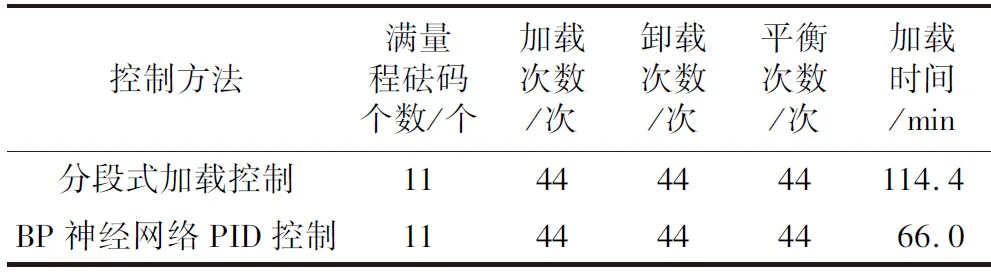
表2 实际应用中的PID控制性能对比Tab.2 Comparison of PID control performance in practical applications
由表2可知,整体检定时间可从114.4 min缩减至66.0 min,效率提升73%。通过更换试验对象、安装方式,其时间不会产生太大差别。
4 结论
本文提出了一种新的BP神经网络PID参数自适应整定算法。该算法应用于3 000 Nm静重式扭矩标准机。基于这种新型控制算法,本文设计出一套新型基于神经网络的PID自适应控制系统软件。通过试验结果可以看出,改进后的算法响应速度和精度都有一定的改善。特别在首次安装加载时,扭矩传感器连接存在间隙,优势更为明显。由此可知,BP神经网络控制效果更好,而且不受传感器种类、安装方式的限制。
该自适应整定控制算法可以有效提高静重式扭矩标准机使用时间和效率,实现静态扭矩标准机智能化自整定、自适应功能。在未来推广后,该算法能减缓企业送检周期与送检成本,推动扭矩量值溯源的发展。该研究为保障人民群众生命安全和社会公共安全提供有力的计量技术支撑,对现代制造业、国防和工程技术有重要意义。

