塑料裂解温控系统的模糊规则提取算法研究
马俊林,曹梦龙
(青岛科技大学自动化与电子工程学院,山东 青岛 266061)
0 引言
塑料裂解过程作为当前工业生产极为重要的一环,主要任务是将废轮胎、废塑料、污油泥、生物质通过裂解技术获得燃料油、可燃气和固态燃料等产品。该过程对于废物回收利用具有重要意义[1]。
裂解炉中的温度控制对于整个系统的热力分布以及产生物料的质量优劣具有重要影响。裂解炉系统产生复杂的理化反应,具有非线性、滞后大、强耦合等不易精准控制的特点。许多工厂对塑料裂解温度控制过分依赖人员经验以及主观意识,使得调控的可靠性不高、控制效果不佳。依靠人工经验法制定模糊规则有时会存在规则重复甚至出错等情况,使得整个模糊控制系统的鲁棒性和准确性下降[1]。一些过分依赖数学模型建立的算法,建立模型的过程繁琐且复杂,难以得到合适的数学模型,并且难以在实际生产过程中广泛应用。
近年来,人们关注从样本数据中自动产生模糊规则。本文着重于利用聚类方法,从裂解过程中的实际样本数据得到数据间的相关程度,建立模糊控制器,对裂解炉中温度指标进行有效控制[2]。
1 塑料裂解技术简介
废塑料裂解是指含有有机物质的废塑料在高温反应器中通过受热裂解,回收理化反应产生的燃料油、固体燃料和可燃气,以实现废塑料最大化废物利用的技术。裂解塑料经过预处理装置洗涤、脱水,加入防结焦小球后进入裂解炉裂解。塑料裂解系统原理如图1所示。
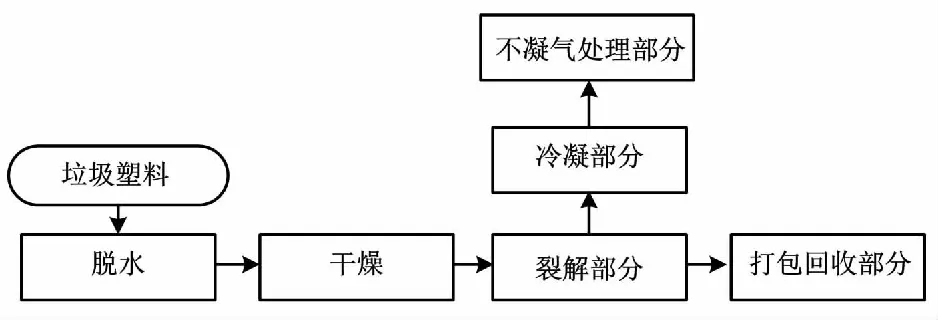
图1 塑料裂解系统原理Fig.1 Principle of plastic cracking system
裂解炉温度是整个系统的重要参数,直接影响物料的分解率。根据实际项目,裂解炉共有三级双螺旋裂解设备,分别对应低温裂解300 ℃、中温裂解400 ℃、高温裂解500 ℃。不同阶段的裂解过程根据不同的冷凝设备和温度调节阀调节,主要依靠风量主调节阀控制通过裂解炉的热空气总流量。3个温度调节阀会根据各温度采样点采集的温度自动调节到合适的开度,保证反应炉的各部位受热均匀。
本文以裂解过程中一级低温裂解炉为研究对象,采用相关性因子改进Wang-Mendal(correlation factor-WM,CWM)算法设计模糊规则以及控制器。首先,针对加热引风机的阀门开度随机某时刻500 s内的加热引风机的阀门开度值,采用不同模糊规则提取算法进行预测。然后,针对低温裂解初始阶段温度控制过程,采用本文算法与其他传统算法进行仿真。最后,通过对比总结出本文模糊控制算法对于塑料裂解温控系统具有更优越的控制效果。
2 模糊规则提取算法及其背景
2.1 Wang-Mendal算法
模糊规则作为模糊控制器的重要部分,前期主要依据人类主观性制定。Wang-Mendal(WM)算法能够有效地从样本数据中提取模糊规则,在一定程度上改善了模糊系统准确性与可靠性不足等问题[3]。现实存在于绝大多数的控制与信号处理问题中的信息,主要分为基于传感器测量的数字信息以及基于专家经验的语言信息。WM算法的中心思想是从现实样本(即数据对和专家经验的语言信息)中提取模糊规则,进而设计控制和处理系统[4]。WM算法主要分为以下内容。
①划分输入与输出的模糊区域,设计每个输入输出区域的“2N+1”个区域间隔,对于不同区域可以不相同。
②从样本数据集中产生初始模糊规则库,并计算每条规则隶属度。选择隶属度最高的模糊区域,并且遍历所有获得的模糊规则[5]。其中,强度最高的规则被保留,而其他产生冲突的模糊规则被消除。
③建立完整的模糊规则库。
④基于模糊规则库设计映射关系(即去模糊化关系),得到输出。
2.2 快速寻找峰值密度算法
快速寻找峰值密度(fast search and find of density peaks,FSFDP)算法是1种常见的聚类算法。在模糊规则提取之前,需要先对样本数据进行分类聚类,即数据预处理。本文选用的FSFDP算法是1种针对大规模样本集的、快速寻找发现密度峰值的聚类算法[6]。本文模糊规则提取算法需要用到样本数据对,但可能存在由于大量噪声值导致的模糊规则可靠性差的问题。利用FSFDP算法能有效消除噪声值。FSFDP算法的中心思想是计算每个数据点周围密度ρi和每点中心偏移距离δi[7]。
通常,计算值(ρi,δi)中二者都大的数据点为聚类中心。FSFDP算法存在2个基本假设:一是聚类中心附近的数据点具有较低密度;二是数据点与其他密度更大的中心点距离较远。FSFDP算法主要分为以下步骤。
①计算数据点任意2点的欧氏距离,并估算截止距离dc。
②计算ρi:
ρi=∑jχ(dij-dc)
(1)
式中:χ(x)为样本集A的指标函数;dij为2个数据点的欧氏距离。
③计算每个数据点的δi以及该点最近邻点编号j。
④估算聚类中心开始聚类,局部密度计算如式(1)所示。
当x<0时,χ(x)=1;其他条件下,χ(x)=0。其中,ρi相当于比截止距离dc更小的数据点的数量。然而,聚类结果受截止距离的影响很大。dc一般为预先设定的截止距离。数据域是在原始数据的基础上提取最优阈值的方法,需选择合适值使平均密度为总数据量的1%~2%。此算法对不同数据点局部密度的相对大小较为敏感。因此,对于数据量大的情况,截止距离的选择对算法精度而言尤为重要[8]。
此外,δi表示每个数据点与密度较大数据点之间的最小距离[9]。
δi=minj:ρj>ρi(dij)
(2)
2.3 减法聚类算法
为了更加准确地获得样本数据的内在规律性,本文采用减法聚类(subtractive clustering,SC)算法获得数据的初始聚类中心。SC算法作为一种基于密度的快速聚类算法,用于优化数据点并获得聚类中心,时间复杂度仅与数据的维度呈线性关系。其原理是把每个数据点都作为聚类中心,按照每个数据点周边的数据密度计算每个数据点成为聚类中心的概率。SC算法与模糊控制系统相结合,可解决模糊C均值算法(fuzzy C-means,FCM)对初始值设定敏感、设置位置不佳而引起的局部最优解的问题。
SC算法的原理为:首先,定义数据点半径,选取第一个聚类中心是周围样本密度最大的数据点;其次,移除半径内所有样本;最后,确定下1个簇及中心并重复此过程,直到所有样本都在1个簇的半径内[10]。
①假设所有数据点都在1个单位超立方体内,定义各数据点密度指标,如式(3)所示。
式中:ra为设定的密度范围;xi为第一个聚类中心,即周围数据密度最高的点。
②数据点根据xi进行修正,如式(4)所示。
一般而言,选取rb=1.5ra,直到剩下数据点可能作为中心点的概率小于设定某个阈值。由于SC算法不需要事先定义聚类中心的数量,可以自适应确定WM算法每个输入量的模糊区域。由于SC算法对于噪声项敏感,所以此算法只可应用在数据预处理(即FSFDP算法优化初始数据点)之后。在预处理阶段之后,根据样本分布可以有效地得到模糊区域和标准差[11]。
③基于FSFDP算法和SC算法的CWM算法。
CWM算法需利用样本数据计算样本相关性。其目的是在WM算法的基础上结合FSFDP算法和SC算法获得完备的模糊规则库,并进一步建立可靠性、鲁棒性高的模糊控制系统。利用此算法提取到的模糊规则采用IF-THEN形式。模糊规则表示为:
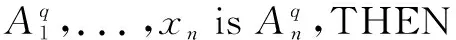

①通过FSFDP算法优化样本集,并计算样本距离与密度值。
②通过SC算法确定变量模糊区域与标准差,划分变量模糊区域并计算高斯隶属度值。
③获得变量的先行参数值,计算每个模糊规则置信度,并采用模糊数学理论优化样本数据集。计算样本权重值,如式(5)所示。
式中:m为输入变量数量;Aij为第i个模糊集;μ为各变量的模糊区间内高斯隶属度函数值。
④根据步骤③计算样本相关性。
⑤选取合适的结果参数值。
⑥提取模糊规则,遍历所有变量的模糊区域以建立完备的模糊规则库。输出值计算式为:
式中:N为所有样本数量;l为当前选择的模糊规则数;c为样本相关性因子;d为样本贡献程度。
贡献程度式及其递推子式如式(7)~式(10)所示。
式中:u为样本数据的模糊隶属度;u*为相关性因子优化更新后的隶属度值[8]。
通过样本相关性可以有效提高算法完备性和鲁棒性。其在计算每条模糊规则贡献度时采用样本的加权平均运算,一定程度上减小了噪声影响。此外,样本相关性应用于改进算法的输出值计算[12]。样本相关性因子ci为:
ci=δiλi,i=1,2,...,N
(11)
式中:λi为第i个样本点的权重值。
CWM算法流程如图2所示。

图2 CWM算法流程图Fig.2 Flowchart of CWM algorithm
3 仿真及分析
3.1 基于Mackey-Glass混沌时间序列仿真试验
本文方法是以非线性大滞后为背景实现的。本节采用本文方法对Mackey-Glass(MG)混沌时间序列进行预测。其中应用到的MG混沌时间序列方程如下。
MG混沌时间序列既不收敛也不发散,具有对初始条件高度敏感的特性。当τ>17,表现为混沌。基于前人使用四阶龙格库塔(Runge-Kutta,RK)方法,采用本文方法对MG方程进行预测。首先作如下假设。
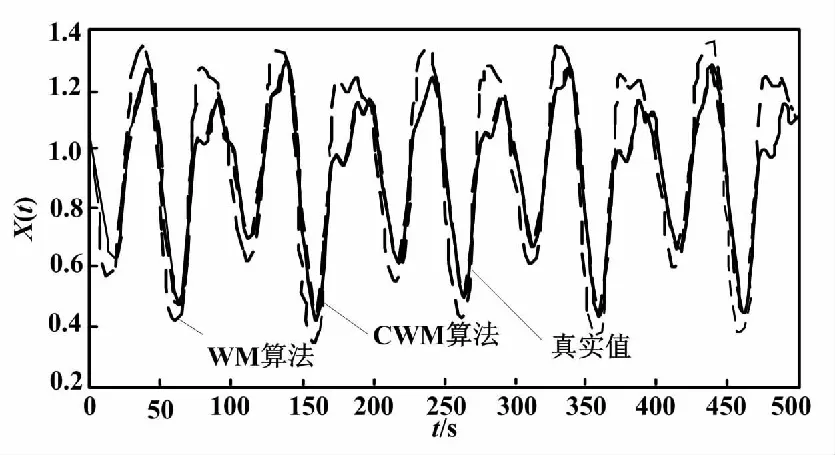
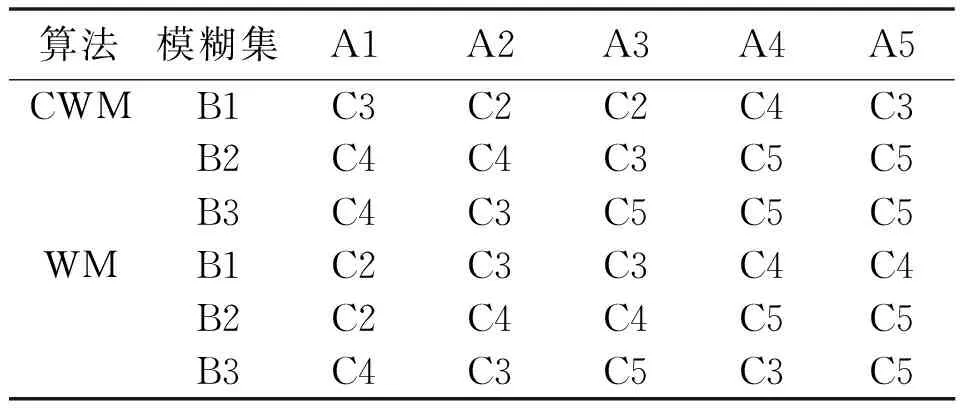
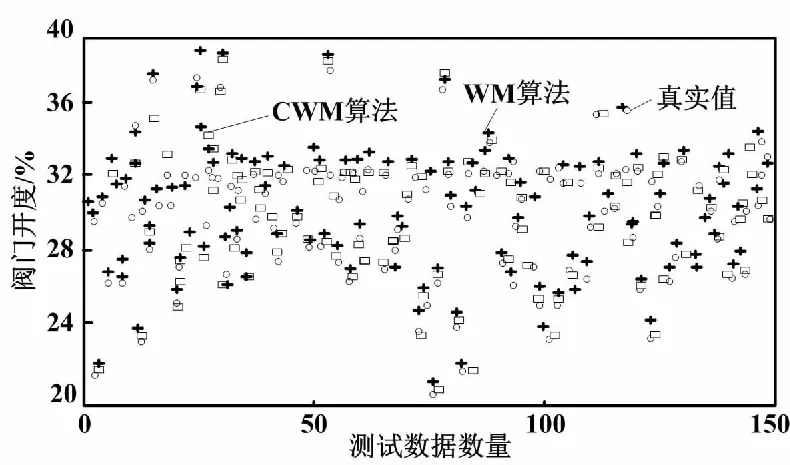
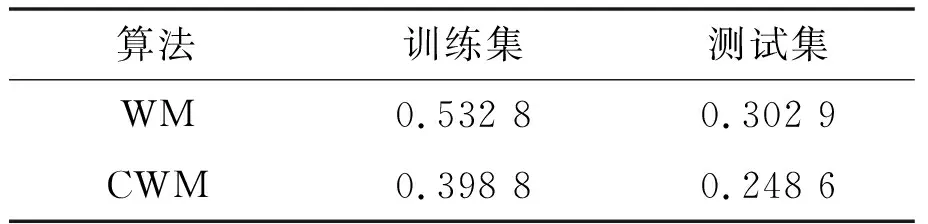
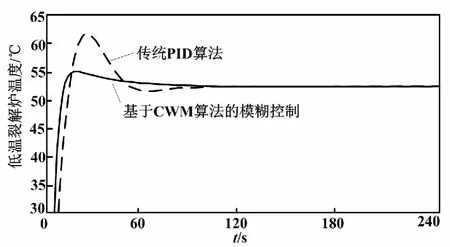
方程中的初始值x(0)=1.2、τ=17且只考虑t>0的情况。选择118 ω(t)=[x(t-18),x(t-12),x(t-6), x(t),x(t+6)] (13) 式(13)中,前四列作为模糊控制器的4个输入值,第五列作为模糊控制器输出值。仿真试验以6个时间间隔为基准,并选用当前状态的前四项状态值作为预测指标。此外,为了验证该算法的鲁棒性,人为加入几项噪声干扰。噪声干扰项数据如表1所示。 表1 噪声干扰项数据Tab.1 Noise interference item data 采用FSFDP算法优化前500个样本点,并将截止距离设定为0.005,进而使用SC算法,得到5个样本中心分别为0.507 2、0.327 0、0.802 6、0.595 9、0.982 5。模糊预测器设计完成后,将测试数据导入其中。CWM算法与WM算法预测数据对比如图3所示。 图3 CWM算法与WM算法预测数据对比图Fig.3 Comparison of prediction data between CWM algorithm and WM algorithm 本节随机在实际塑料裂解低温炉中选择50例温度样本数据,并计算当前数据点温差与温差变化率。两者均为控制器输入。裂解炉风机风量阀开度为控制器输出。以150例样本数据作为控制器测试数据,并选用均方误差(mean-square error,MSE)作为比较误差的标准。均方误差的计算如式(14)所示。 式中:E为均方误差(mean squared error,MSE)值,采用统计学中达依拉准则对样本数据进行分析。 首先,确定第一个输入量(即温差的平均值)为4.433 3;第二个输入量(即温差变化率的平均值)为10.946 7。然后,确定2个输入量的论域变化范围分别为{-51,56}、 {-41,44},输出量的论域变化范围为{10,69}。最后,将2个输入量分别划分为5个和3个模糊区域并制定规则。算法采用高斯隶属度函数计算样本相关性。CWM算法与WM算法制定规则对比如表2所示。 表2 CWM算法与WM算法制定规则对比Tab.2 Comparison of development rules between CWM algorithm and WM algorithm 二维数据散点对比如图4所示。 图4 二维数据散点对比图Fig.4 Comparison of two-dimensional data scatter comparisonCWM CWM算法与WM算法误差对比如图5所示。 图5 CWM算法与WM算法误差对比图Fig.5 Comparison of errors between CWM algorithm and WM algorithm CWM CWM算法与WM算法的MSE对比如表3所示。 表3 CWM算法与WM算法的MSE对比Tab.3 MSE comparison between CWM algorithm and WM algorthm 由图5与表3可知,在其他条件相同的情况下,CWM算法得到的模糊规则更加合理且可靠性更高。式(14)可计算MSE。通过分析2种算法的预测结果可知,CWM算法相比WM算法误差值较小。 为了更直观地对裂解炉内温度变化情况进行分析,以下选取裂解过程中的低温裂解阶段进行研究。仿真以裂解初始阶段前4 min内炉内升温过程作为参考,将基于常规比例积分微分(proportional integral differential,PID)算法与本文改进模糊规则提取算法分别应用在上述过程中。2种控制算法温度对比如图6所示。由图6所示的对比结果表明,本文算法相比传统PID算法在前1 min内超调量减少12.7%,响应时间也大致提前3~5 s。因此,本文算法能够满足裂解过程的温度控制要求且具有较高优越性。 图6 2种控制算法温度对比图Fig.6 Temperature comparison of two control algorithms 本文主要对1种从样本数据提取模糊规则的改进算法进行研究。改进算法首先对样本数据通过2种聚类算法进行数据预处理,FSFDP算法用以优化原始数据集,从而减少噪声项和减少数据集的规格;然后引进相关性因子,计算得出模糊控制器输出值。本文后半部分通过总结前人经验以及塑料裂解样本数据,得到2种常见提取规则算法的预测结果对比以及误差分析对比。根据对比结果可知,本文中的改进CWM算法与传统WM算法、传统PID算法相比,具有更高的准确性和鲁棒性,能够满足塑料裂解工艺的温度控制要求。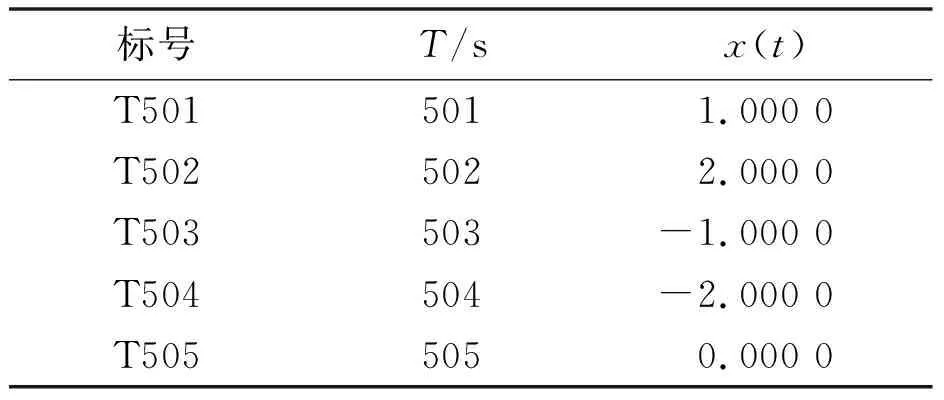
3.2 基于塑料裂解样本数据仿真试验

4 结论

