异质性预期混合寡头模型均衡解的复杂性分析

赵欣宇

(辽宁师范大学 数学学院，辽宁 大连 116029)

近年来，国企民营化混合所有制改革一直是研究的热点问题之一，如何实行国企民营化则成为人们长期争论的焦点.国内外学者从不同角度提出了各自的见解，其中影响最大的当属混合寡头理论的出现，为混合所有制改革提供了一定的理论基础.Matsumura[1]为混合寡头理论作出了奠基性贡献，把产权改革引入混合寡头理论；Wang和Han[2]引入了公司治理因素，分析了国企治理对最优民营化政策的作用；Pal和Saha[3]、Xu等[4]通过分析最优民营化和排放税两个因素，认为部分民营化是最优选择；Gil-Moltó等[5]分析了民营化对于最优研发补贴和社会福利的影响.国内学者刘小玄[6]较早讨论了如何才能实现帕累托改进的最优化；徐晓慧和李杰[7]研究了在开放环境下民营化程度对于企业政策的决定以及社会福利的影响；杨紫宁[8]探讨了国有企业的民营化水平对最优减排、减排补贴率的影响；陈晓珊和刘洪铎[9]构建了混合寡头模型，对政府补助如何影响高管薪酬及高管薪酬进行了理论与实证分析；叶光亮等[10]基于产业链的垂直市场结构设计理论模型，从控制权角度探讨混合所有制企业中的国有持股比例与产业链中双重边际化现象的关系.上述文献无疑丰富了混合寡头理论，但他们都是基于完全理性条件下，静态分析了纳什均衡结果.而现实中的市场信息是不完全的，寡头不可能完全理性地作出决策，需要经过多次重复博弈，通过动态演化过程才能最终达到均衡.为此，本文利用非线性动力学理论，建立了异质性预期下混合寡头博弈模型，分析了均衡点的存在性与稳定性问题，讨论了各个因素对系统所处均衡状态及利润造成的影响，并数值仿真了不同市场参数条件下的系统动态行为.

1 基本模型的假设与建立

假设在混合所有制经济下有两个生产同质产品的混合寡头垄断国有企业1与民营企业2，qi(i=1,2)表示企业产量，每个企业的产量可表示为线性逆需求函数形式p(Q)=a-Q，其中，a>0，Q=q1+q2.每个企业的成本函数为线性形式Ci(qi)=ciqi，i=1,2.对于边际成本ci，做如下规定也许更具有普遍意义，鉴于国企特殊产权导致国企产品的平均成本c1大于民营企业的平均成本c2，不妨设c1=βc2，其中，β>1，表示边际成本差异度，β越大，企业效率就越低.因此企业的利润函数为

πi=p(Q)qi-Ci(qi)=(a-Q-ci)qi，i=1,2

(1)

假设两企业的目标支付函数用Ui表示.民企的目标是为了单纯地追求利润最大化，即其目标函数为

(2)

对民营化的国有企业，简称国有企业，遵循主流的“追求利润与社会福利的加权平均值最大化”原则.设民营资本产权所占比例为θ，则国有企业的目标函数可描述为

(3)

对式(2)与式(3)分别求导，可得到两企业的一阶最优条件分别为

(4)

由此可得混合寡头的均衡产量为

(5)

由于混合寡头垄断市场是一个不完全信息的多期动态博弈过程，每个企业掌握的市场信息并不充分，每一期都会尽可能地根据自己的学习适应性作出有限理性决策.考虑到国有企业是大型企业，市场占有率高，市场资源丰富、处理市场信息的能力比民营企业强，因此假设国有企业采用有限理性决策，即利用边际利润与本期价格来调整下一期的价格.当本期边际利润为正(负)数时，它将在下一期适当提高(降低)产量以获得更高利润.因此其产量决策模型可表示为

(6)

其中，α>0，表示产量调整速度.

民营企业虽然有技术、价格优势，但市场规模小，管理经验不丰富、处理市场信息能力不足，不具备足够的产品产量调整能力，因此假设民营企业具有天真预期决策能力，只能根据自身边际利润的反应函数进行产量决策，即其下期产量是基于本期对其他企业产量最优反应，其在时期t+1的产量决策模型为

(7)

于是两混合寡头企业根据自己不同的理性决策行为，形成产量博弈二维离散复杂动态系统为

(8)

2 模型的均衡解和局部稳定性分析

令qi(t+1)=qi(t)=qi，得动态系统(8)相对应的代数系统为

(9)

为使均衡点有经济意义，参数应满足如下条件

(10)

为研究均衡点局部稳定性，首先求出动态系统(8)的雅克比矩阵，即

(11)

根据系统均衡点的稳定性条件，当且仅当对应雅克比矩阵的所有特征值|λi|<1，i=1,2时，均衡点才是稳定的.为此有下面结论：

定理1边界均衡点E1是不稳定的.

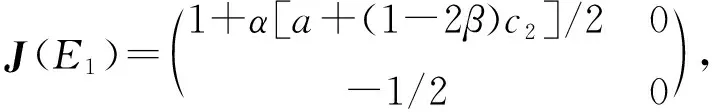
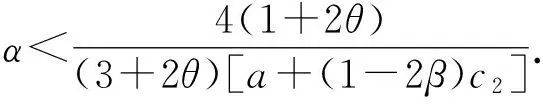
证纳什均衡点E2的雅克比矩阵为

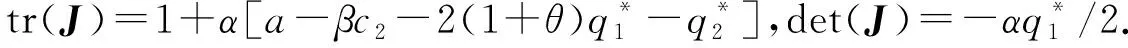
因tr2(J)-4det(J)>0，特征根是实数，该系统稳定的充要条件满足Jury判据，即(1)1-tr(J)+det(J)>0，(2)1+tr(J)+det(J)>0，(3)det(J)<1.

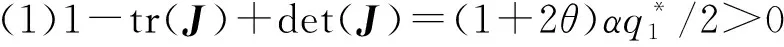
3 数值模拟

为更好理解各参量对系统(8)动态行为的影响，下面对其进行数值模拟分析.不妨取参数a=10，c2=3，β=1.5.

3.1 国企产量调整速度对均衡产量与利润的影响

取民营化水平θ=0.3，其他参数取上述初始值，均衡产量的动态演化过程如图1所示.从图1看出，当国企产量调整速度在0<θ<0.44时，两混合寡头的产量出于均衡稳定状态，当θ=0.44时，系统发生倍周期分岔，甚至出现了混沌现象，由此导致混合寡头的利润也发生相应变化.图2描述的是两混合寡头的平均利润及平均最大社会福利随产量调整速度变化的演进过程，可以发现，从系统失稳开始，最大社会福利与国有企业的平均利润是下降的，而民营企业的利润却在上升.即产量调整速度太大对国企与整个社会没有任何好处，但却对民营企业有利.

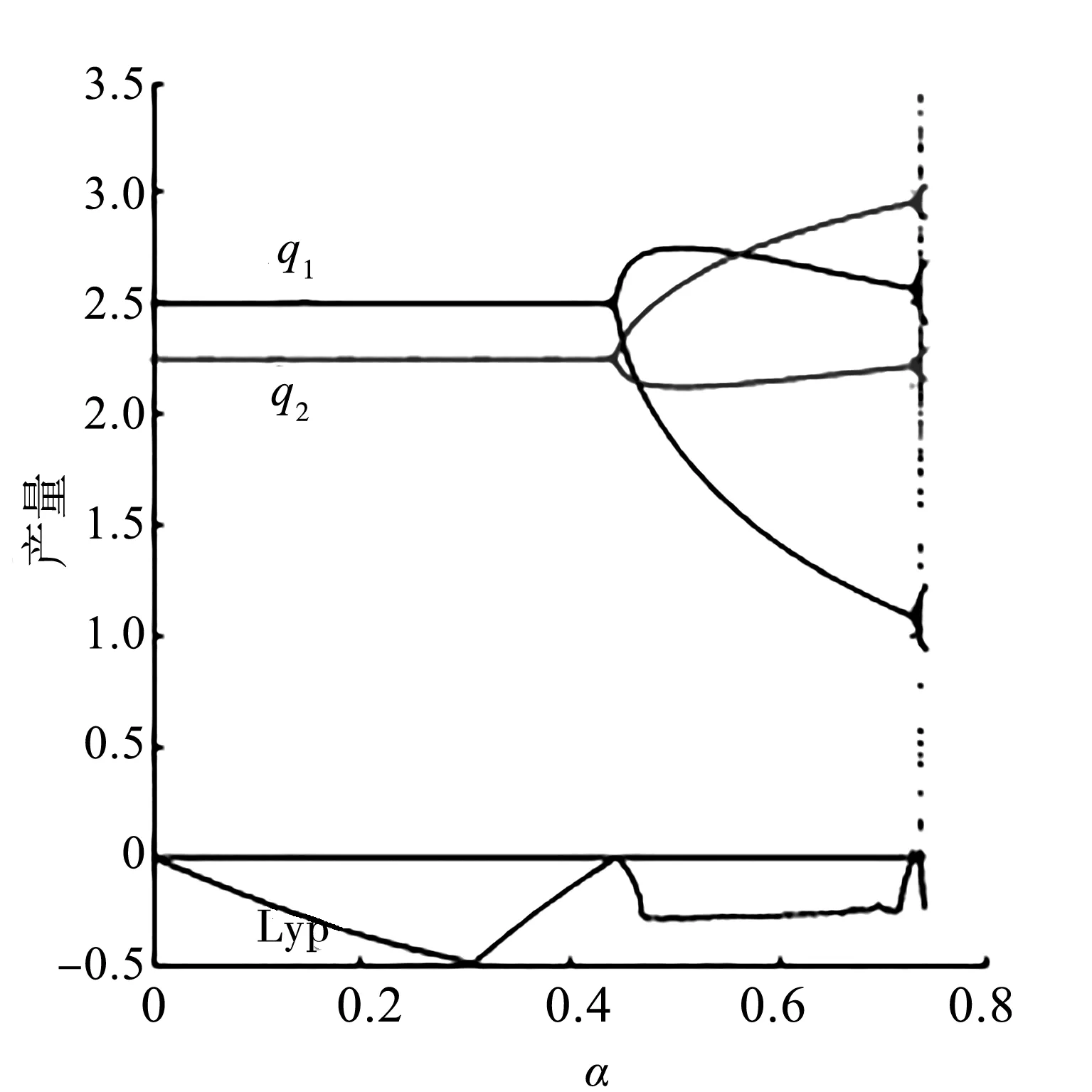
图1 产量随α变化分岔图Fig.1 Bifurcation diagram of output with α

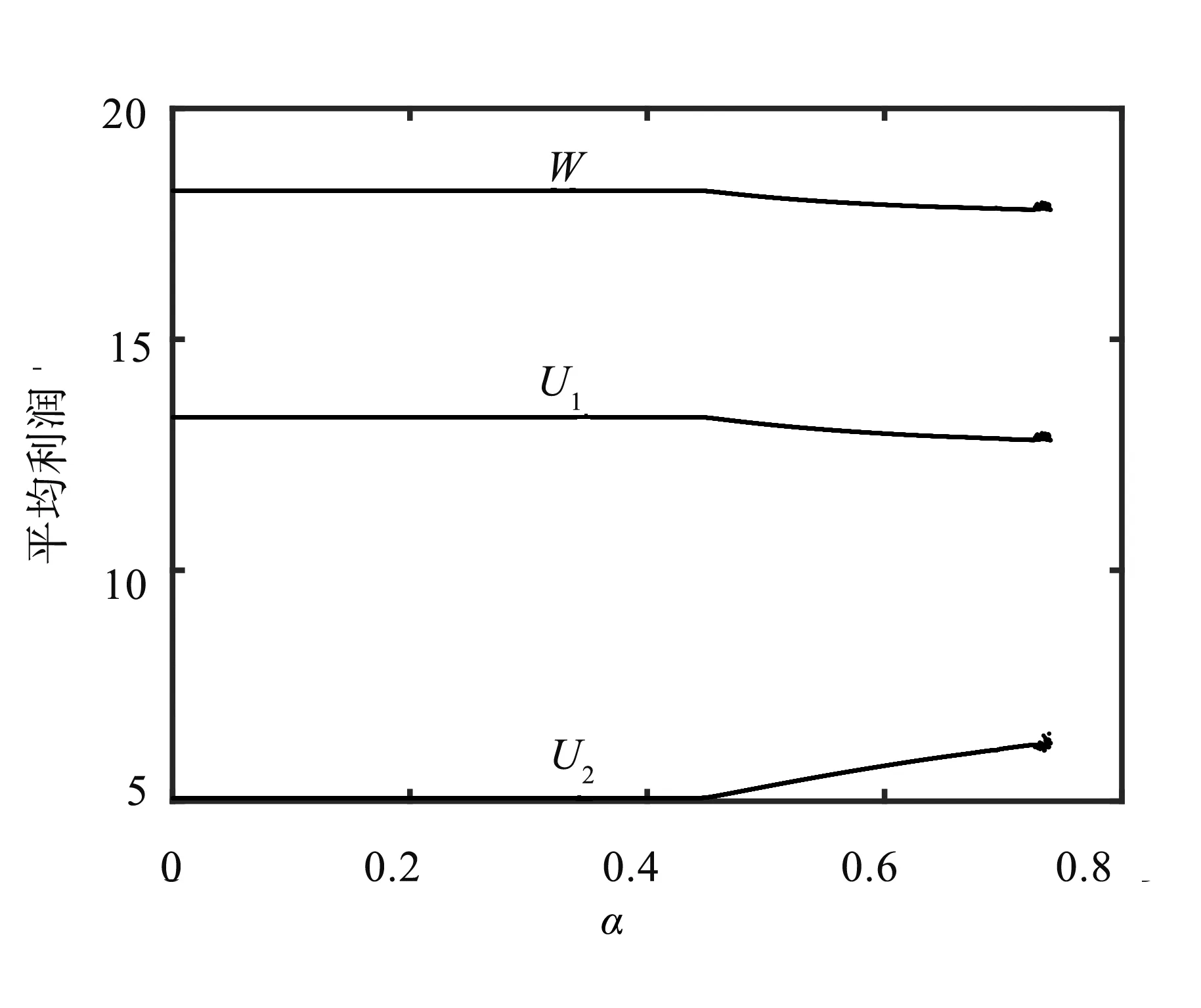
图2 平均利润随α变化演化图Fig.2 Evolution diagram of average profit with α

3.2 民营化水平对均衡产量与利润的影响

取产量调整速度分别为α=0.4和α=0.5，其他参数取上述初始值时，混合寡头均衡产量随民营化水平变化的动态演化过程如图3所示.可以看出，随着民营化水平的提高，国企的产量逐渐减少，而民营企业的产量逐渐增大，且民营化水平越低，两寡头的产量越容易出现分岔现象，这种分岔现象伴随着产量调整速度的增大而变得越来越显著.图4描述的是平均利润和最大社会福利随民营化水平的演变过程，可以看出，伴随着民营化水平的不断提高，虽然国有企业的平均利润下降，但民营企业与最大社会福利的水平却在提高，对整个社会是有益处的，这也是政府大力推进国有民营化的主要原因.

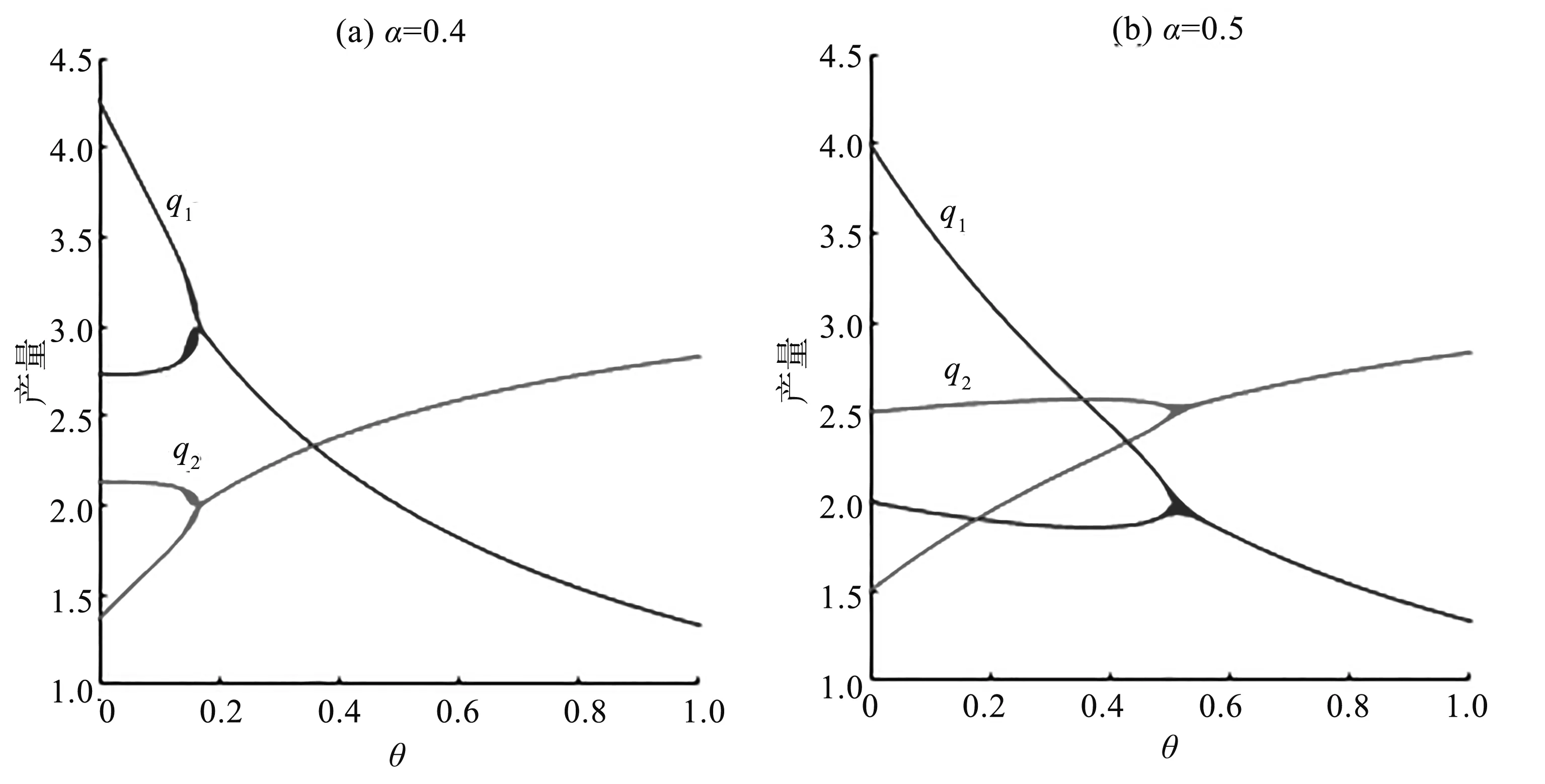
图3 产量随θ变化的分岔图Fig.3 Bifurcation diagram of output with θ

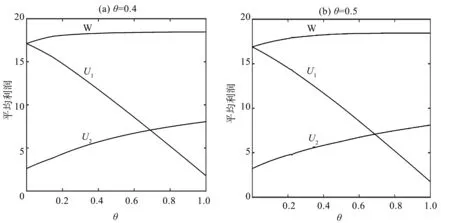
图4 平均利润随θ变化的演化图Fig.4 Evolution diagram of average profit with θ

3.3 生产成本差异度对均衡产量与利润的影响

图5和图6分别给出了α=0.3，θ=0.3时国企占主导下均衡产量与平均利润随生产成本差异化变化的演化.当民企成本很小，即β<1.18时，均衡产量出现分岔现象，伴随着民营成本优势扩大，当1.18<β<2.2时，导致民企产量增高与国企产量降低，直至国企产量为0.当民企成本优势过大，即β>4.35时，两寡头产量又出现分岔混沌现象.与此相对应的平均利润起初是国企与社会总福利的减少及民企利润的增加，显示出民营企业的成本优势.一旦民企的这种成本优势足够大，那么将使其在市场上占据主导地位，此时民营企业的利润反而没有增加，这也是成本优势过大的民营企业不愿与国企合作的原因.

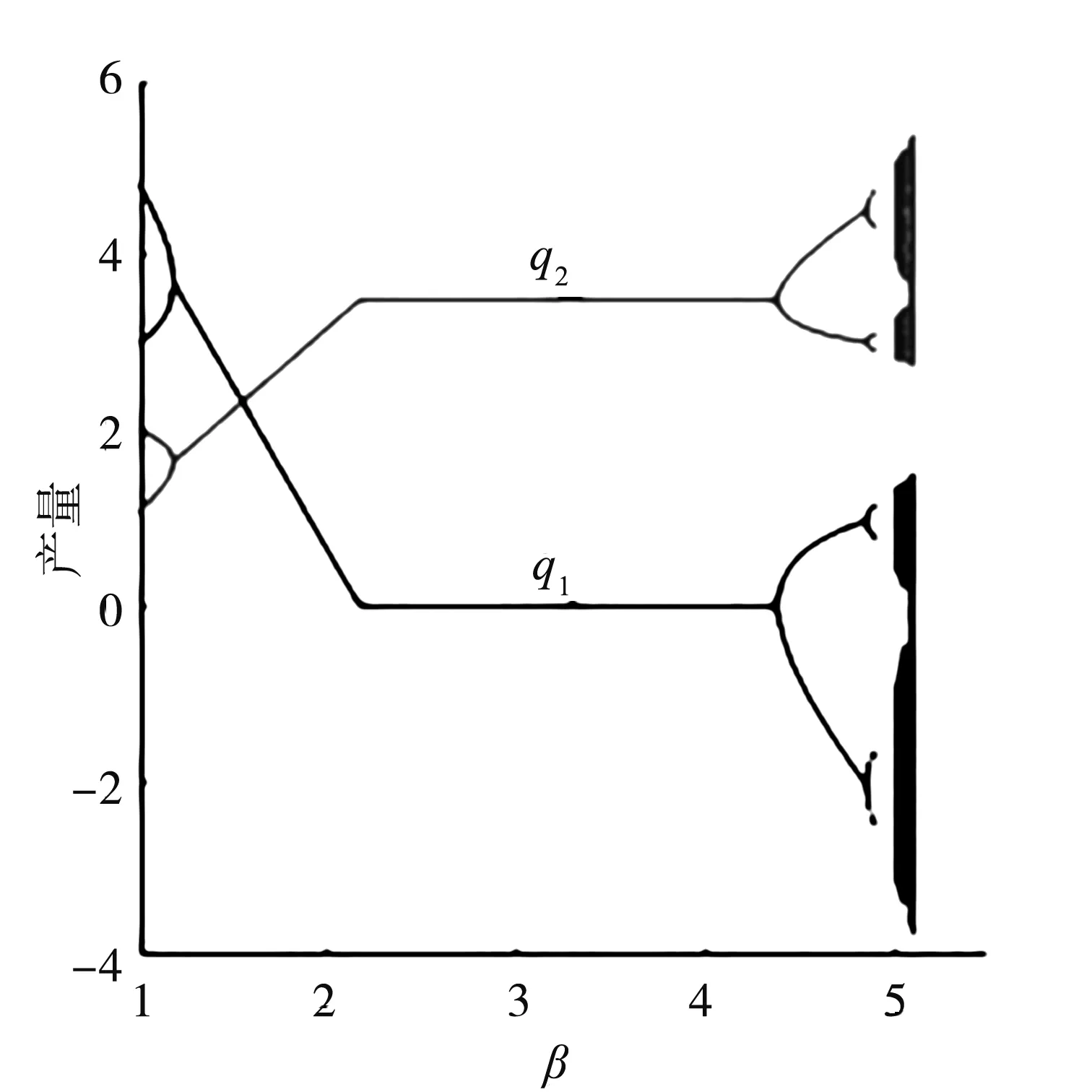
图5 产量随β变化分岔图Fig.5 Bifurcation diagram of output with β

图6 平均利润随β变化演化图Fig.6 Evolution diagram of average profit with β

4 结束语

本文建立了异质性预期的混合寡头竞争博弈模型，分析了模型均衡点的稳定性及影响因素，并对博弈过程进行了数值仿真，结果表明:民营化水平越高，成本差异化越小，均衡产量就越稳定；国企产量调整速度过快对其本身和社会福利没有任何好处，但却对民企企业有利；民营化水平越高，国企产量就越低，利润就越小，而民营企业产量则提高，其利润及社会福利水平也提升，提高了社会总体效率；成本的差异会导致更高的民企产量与更小的国企产量，当民企成本优势过大时，会导致国有企业民营化改革的失败.