基于长短期记忆神经网络的油井产液量和含水率预测方法

赵洪涛，李金泽，杨 毅，赵洪绪，房鑫磊，于伟强

(1.中法渤海地质服务有限公司，天津 300457；2.中海石油(中国)有限公司天津分公司，天津 300459)

掌握油井产量变化规律是实现油田高效生产与管理的关键[1]。由于油藏地质、举升工艺、作业措施、管理水平等均具有复杂性，油井产量的影响因素众多，为准确预测油井产量带来巨大挑战[2]。传统的产量预测多采用基于渗流理论的油藏工程方法或者油藏数值模拟方法[3-5]，然而，这些传统方法或者因基于理想渗流情况而不能反映实际储层渗流情况，或者因需要大量地质、流体物性和开发动态等方面的数据，致使结果受历史拟合和地质建模的影响[6]。

近年来，随着人工智能技术发展，机器学习方法被大量用于油井产量预测，并取得了良好的预测效果[7-12]。2018年，Loh等人[13]将长短期记忆神经网络(LSTM)用于短期产量预测，可以准确捕捉生产动态并预测短期生产。周于浩等[14]构建了基于门控递归单元(GRU)的神经网络产量预测模型，相比于长短期记忆神经网络而言，门控递归单元方法可大幅减少运行参数，提高运算及记忆性能。2021年，Cheng & Yang[15]研究指出，长短期记忆神经网络适合用于特征参数多和数据量多的开发区，而门控递归单元适用于数据较少的开发区。2019年，谷建伟等[16]选取排量、泵深、生产时间、含水率、动液面、气油比、邻井注水量和邻井产液量作为影响油井产量的参数，建立长短期记忆神经网络油井产量预测模型，实现油井产量准确预测。2020年，刘巍等[1]考虑油井和周围注水井的油藏静态资料和开发动态参数，建立了一种利用机器学习模型实现油井日产油量的快速预测方法。王洪亮等[17]在对32个产量影响因素分析的基础上，采用长短期记忆神经网络模型进行产量预测，发现该方法的预测结果优于传统水驱曲线方法和全连接神经网络(FCNN)方法。2021年，张瑞和贾虎[18]将井组内不同生产井产油量和注水井注水量作为相关时间序列，建立基于多变量时间序列(MTS)和向量自回归(VAR)机器学习模型的油井产量预测方法。2022年，Ng等[19]利用元启发式算法(MA)和机器学习算法对Volve油田生产数据进行产量预测研究，并对7种数据驱动模型的预测性能进行评价，发现长短期记忆神经网络在训练结果和预测准确性方面均优于其他6个模型。

从现有研究来看，采用长短期记忆神经网络方法可以获得较好的油井产量预测效果。但大多数研究方法所需的参数较多，数据收集困难，并且往往将注水井总注入量作为一个特征参数来考虑，未考虑分层注水对油井产量的影响。本文以分层注水区块为研究对象，首先采用平均不纯度减少(MDI)方法分析区块中所有分注层段对单井产量和含水率的影响程度；然后，根据重要性确定出主要的分注层段，实现数据降维；最后，利用筛选出的分注层段的注水数据以及油井日产量和含水率数据对长短期记忆神经网络模型进行训练和优化，得到最终的单口油井产量和含水率预测模型。为简便、快捷、准确预测油井产量和含水率变化提供一种新的手段。

1 理论与方法

1.1 特征参数提取方法

油井产量受储量、储层物性、举升工艺、储层措施、油水井数量、采油速度、生产时间等因素影响[1，20]，其最终关系表现在注入井和生产井的参数上。本文将中间影响因素作为“黑盒子”，仅考虑注入量与采出量之间的关联关系。对于一个分层注水的井组来讲，距离和层位不同的注水层段对生产井的贡献不同。为了降低计算维度、提高计算精度，有必要对影响油井产量和含水率的主要注水层段特征参数进行筛选。

目前机器学习中常用的特征参数提取方法主要有过滤法、包裹法和嵌入法。三种方法的优缺点如表1所示。

表1 特征参数提取方法比较

由表1可以看出，嵌入法在解决过拟合、参数忽略等方面具有较大优势，而基于正则项的特征选择方法不利于优化求解[21]，因此本文最终采用了基于随机森林的特征选择方法。随机森林是一种集成学习算法，被广泛应用于研究各种分类、预测、特征选择等问题[19]。算法提供了平均不纯度减少(MDI)和平均精确度减少(MDA)两种特征选择方法。平均不纯度减少表示每个特征对误差的平均减少程度，常用于确定特征的重要性。对于每一个特征，计算其在每棵决策树中减少的不纯度，然后求其平均值，得到该特征减少的平均不纯度。平均不纯度减少越多，说明在决策树训练过程中的作用越大，则该特征的重要程度越大[22]。平均精确度减少是通过打乱某个特征的特征值顺序，度量顺序变动对于模型精确率的影响。对于不重要的特征，打乱顺序对模型的精确率影响不会太大；但是对于重要的特征，打乱顺序就会降低模型的精确率[23]。这两种特征重要性评估方法对异常值和噪声具有很好的容忍度，不易出现过度拟合等现象[24]。本文选用平均不纯度减少方法筛选影响油井产量和含水率的主要注水层段特征参数[1]。

1.2 长短期记忆神经网络工作原理

递归神经网络(RNN)具有自循环结构，可以将前一时刻的信息传递到下一时刻的计算中，使递归神经网络的输出同时受当前时刻输入和过去所有时刻输入的共同影响[25]。因此递归神经网络在解决时间序列问题方面具有明显优势。递归神经网络的结构如图1所示。

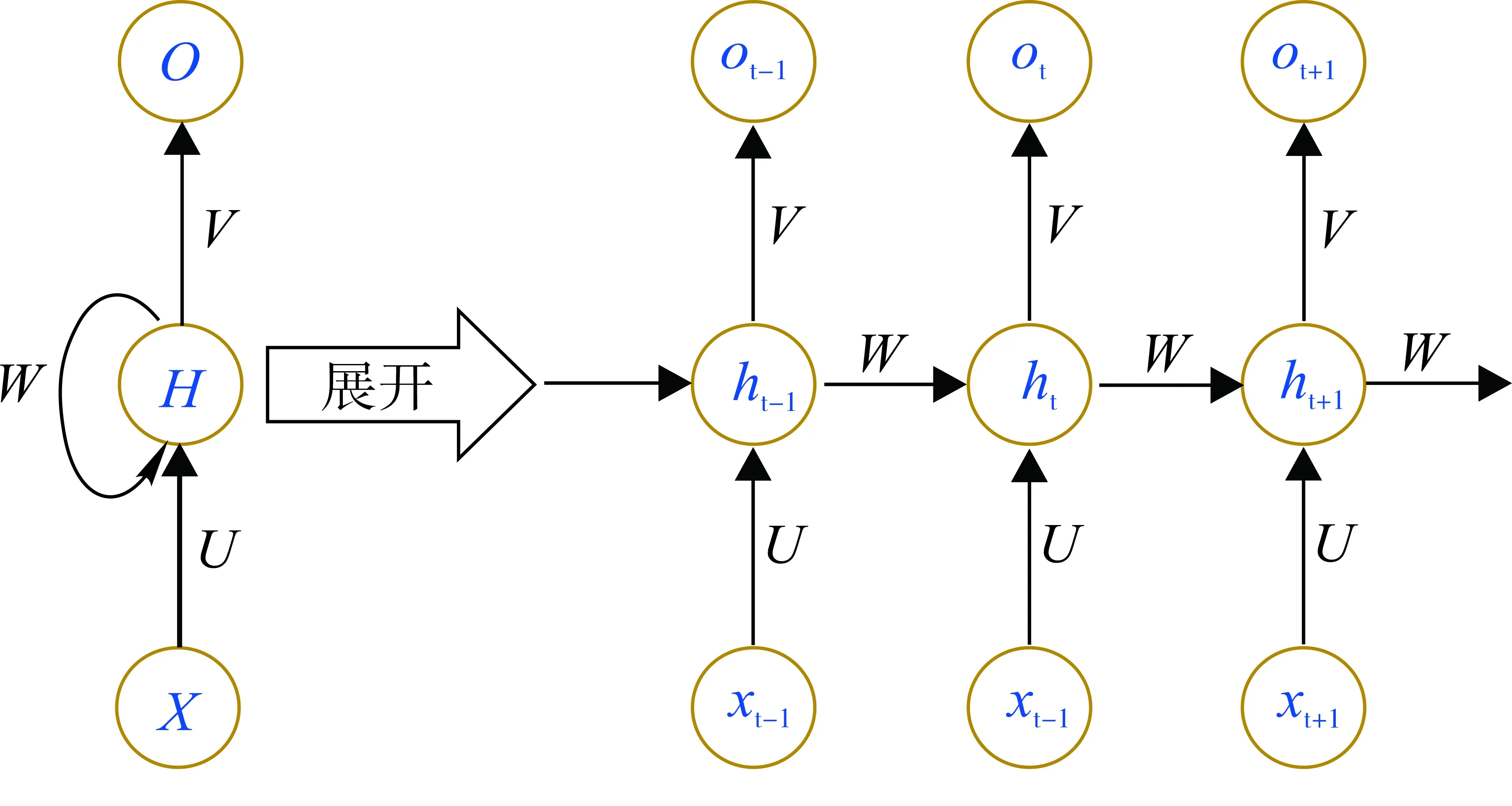
图1 递归神经网络结构

在t=0时刻，对U、V、W进行随机初始化，该时刻的状态h0通常初始化为0；在t=1时刻，其隐藏状态h1和输出o1表示为：

h1=f(Ux1+Wh0)

(1)

o1=g(Vh1)

(2)

式中：h0，h1分别为t=0，1时刻的隐藏状态；f为输入层激活函数，通常为tanh、ReLU、logistic；g为输出层激活函数，通常为softmax；U为从输入层到隐藏层的权重；V为从隐藏层到输出层的权重；W为从隐藏层到隐藏层的权重；x1为t=1时刻的输入；o1为t=1时刻的输出。

当t=2时，隐藏状态h1作为记忆状态参与本时刻的预测活动，即：

h2=f(Ux2+Wh1)

(3)

o2=g(Vh2)

(4)

式中：h2为t=2时刻的隐藏状态；x2为t=2时刻的输入；o2为t=2时刻的输出。

以此类推，递归神经网络的计算公式为：

ht=f(Uxt+Wht-1)

(5)

ot=g(Vht)

(6)

式中：ht、ht-1为t、t-1时刻的隐藏状态；xt为t时刻的输入；ot为t时刻的输出。

长短期记忆神经网络是一种改进的递归神经网络，其准确性、计算速度和可靠性优于递归神经网络，因此适用于油田生产的长时时序预测。长短期记忆神经网络在递归神经网络的基础上增加了输入门、输出门和遗忘门，其结构如图2所示。

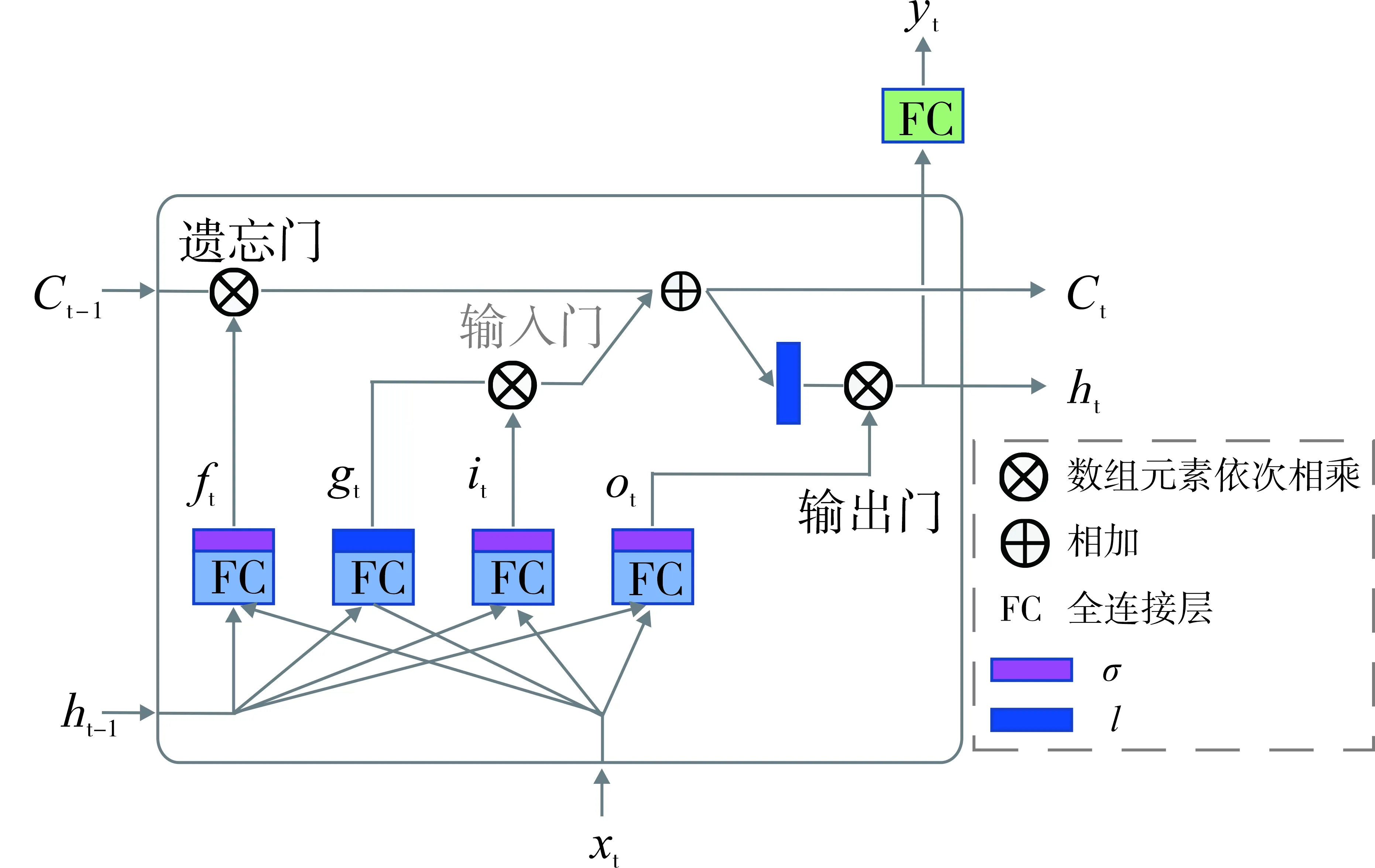
图2 长短期记忆神经网络结构

在t时刻，长短期记忆神经网络单元通过处理输入状态xt、短期隐藏状态ht-1和长期隐藏状态ct-1来生成输出状态yt。长期隐藏状态ct-1包含t时刻之前时间步的相关信息，短期隐藏状态ht-1包含上一个时间步的信息。

遗忘门决定t时刻ct-1被遗忘的部分，通过执行ft和ct-1之间的数组元素相乘来实现，当ct-1里的元素被0相乘则全部遗忘，被1相乘则全部保留。输入门通过执行gt和it之间的数组元素相乘来决定在长期隐藏状态中gt被保存的部分。遗忘门信息(ft⊗ct-1)和输入门信息(gt⊗it)相结合得到时刻t的长期隐藏状态(ct)，表达式为：

ct=ft⊗ct-1+gt⊗it

(7)

式中：⊗表示数组元素依次相乘。

输出门处理新的长期隐藏状态ct和输出向量ot来生成新的短期隐藏状态ht，表达式为：

ht=ot⊗f(ct)

(8)

输入状态xt和短期隐藏状态ht-1通过全连接层FC进行处理，其中gt、ft、it、ot分别为：

(9)

(10)

(11)

(12)

式中：l为非线性激活函数，一般为tanh或ReLU；σ为激活函数，通常为Sigmoid；ft、gt及it、ot分别为控制遗忘门、输入门和输出门，值由激活函数σ和l决定，取值范围[0～1]；Wxg、Wxf、Wxi、Wxo分别为四个全连接层处理输入xt的权重矩阵；Whg、Whf、Whi、Who分别为四个全连接层处理短期隐藏状态ht-1的权重矩阵；bg、bf、bi、bo为偏置项。

长短期记忆神经网络模型训练的好坏采用决定系数和平均相对误差来评价。

1.3 数据归一化处理方法

对数据进行归一化可以提升长短期记忆神经网络模型计算精度，让不同维度之间的特征在数值上有一定的可比性。同时，数据归一化还可以提升长短期记忆神经网络模型的收敛速度，更容易收敛得到最优解。

本文采取最大最小归一化方法将数据映射到[0，1]区间[1]，计算公式如下：

(13)

式中：X为某特征(如分层注水量、油井产量、含水率)归一化后的数据；x为某特征(如分层注水量、油井产量、含水率)待归一化的数据；xmin为该特征的最小值；xmax为该特征的最大值。

1.4 油井产液量和含水率预测步骤

基于长短期记忆神经网络的油井产液量和含水率预测步骤包括：①确定数据集并将数据集划分为训练集和测试集；②利用平均不纯度减少方法分析井组中所有注水井的各个注水层段对每口油井产液量和含水率的重要程度，筛选出影响每口油井产液量和含水率的主要注水层段；③对各个注水层段注水量、油井产液量和含水率分别进行归一化处理，建立归一化的机器学习数据集；④利用训练集数据训练长短期记忆神经网络模型，得到预测模型；⑤利用测试集数据测试长短期记忆神经网络模型的预测效果。

2 现场应用

2.1 数据样本

以海上某区块作为研究对象，该区块描述含油砂体16个、潜力含油砂体18个，探明石油地质储量750×104t、潜力石油地质储量近1 000×104t[17]。目前共有生产井60口、分层注水井44口。根据断层情况，该区块划分成10个注采井组。选取其中一个井组作为预测油井产液量和含水率的研究对象。该井组于2015年11月30日投产，最初采用合注方式生产，2019年8月16日开始采取分注措施，目前包括20口生产井和13口注水井。本文以研究分层注水量对油井产液量和含水率的影响为目的，选取注水井各分层注水量为特征参数，不考虑油井之间的相互影响，收集和整理自分注开始至2021年2月13日的分层注水量、油井日产液量和油井含水率数据，并进行研究。该区块生产井产液量和含水率波动大，采用传统的油藏工程方法难以进行生产预测。

2.2 特征选择

利用平均不纯度减少方法进行特征选择的目的是分析井组内各个注水井层段注水量对每口生产井产液量和含水率的影响程度，剔除影响较小的注水井层段，实现特征参数空间维数的压缩，以提高长短期记忆神经网络训练模型的准确度。以生产井B29井为例，利用随机森林分类函数进行平均不纯度减少分析，计算各个注水井层段的重要性，结果如图3所示。

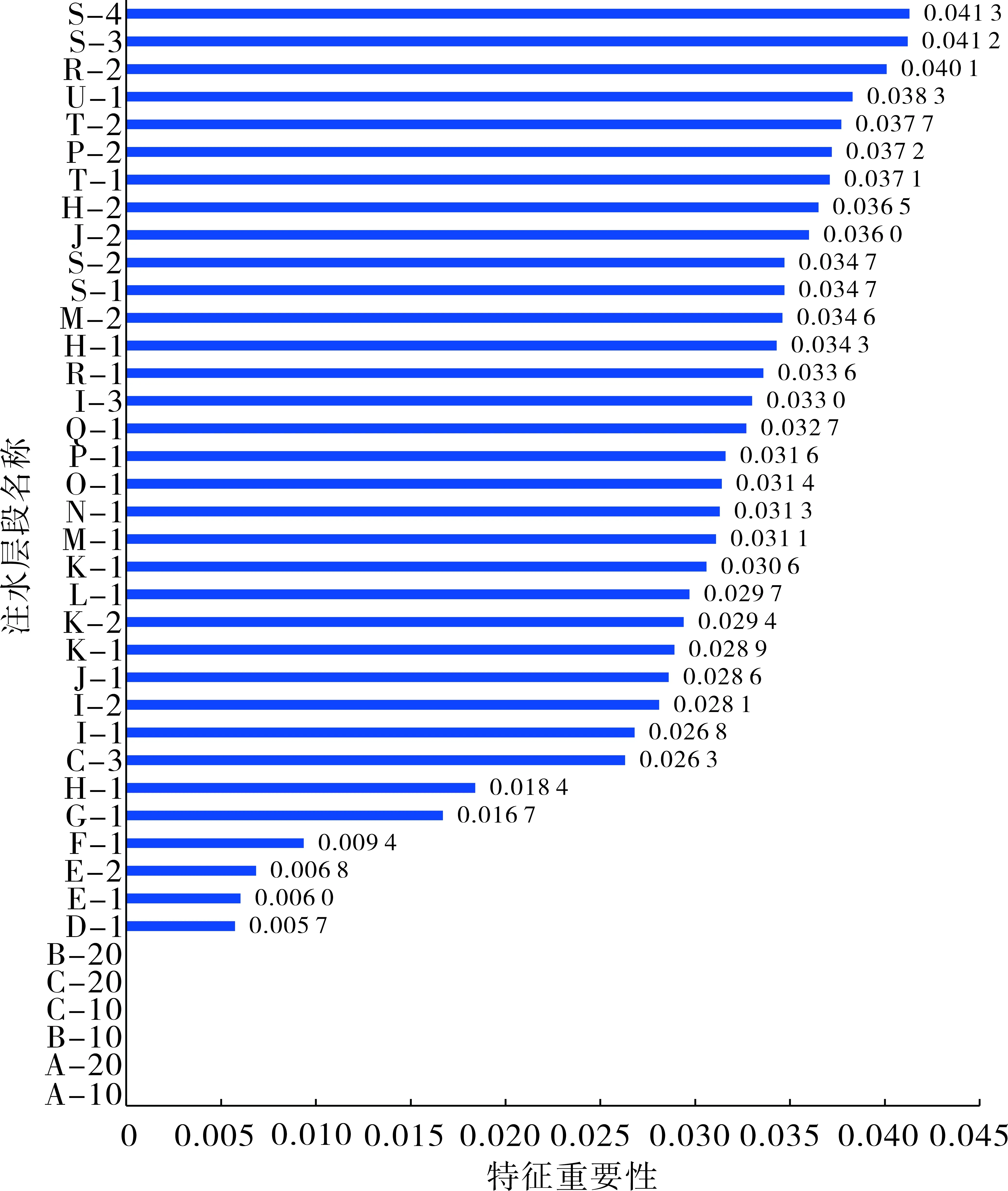
图3 B29井平均不纯度减少特征重要性杆状图

图3横坐标为井组内所有注水井各个注水层段的平均不纯度减少值(即特征重要性)，平均不纯度减少值越大说明该层段的注水量对B29井产液量和含水率的影响越大。从图中可以看出：S-4、S-3和R-2三个层段对B29井产液量和含水率的影响大。剔除排序靠后的、累计值为15%的16个注水层段，保留前24个注水层段作为LSTM的输入特征参数。

2.3 LSTM模型训练与预测

长短期记忆神经网络的逻辑是输入前n天某口生产井的产液量和含水率以及筛选出的注水层段的注水量，预测第n+1天产液量和含水率；接着按照一定步长移动这个n天时间步，来预测下一个n+1天产液量和含水率，从而实现整个数据集的迭代计算。为了防止过度拟合，长短期记忆神经网络模型训练过程中添加忽略层，在每次训练时随机忽略一些神经元(比例一般为20%～40%)。长短期记忆神经网络模型训练过程中的其他网络结构参数取值分别为：时间步长5 d、批次大小128、第一层内神经元数目128、第二层内神经元数目128、随机忽略的神经元比例20%、训练次数为480次。

根据B29井特征选择结果剔除冗余特征后，剩余特征与B29井产液量和含水率构成数据集，归一化数据集后以82的比例将数据集划分为训练集和测试集；然后利用选择的超参数进行长短期记忆神经网络模型训练，选择均方误差作为损失函数；训练结束后反归一化处理，计算决定系数和平均相对误差来判断训练模型的好坏。模型训练过程中训练集和测试集的损失函数随训练次数的变化如图4所示。可以看出，训练集和测试集的损失函数随训练次数的增加逐渐减小并趋于稳定，且两者非常接近，说明长短期记忆神经网络模型训练过程中没有出现过拟合或欠拟合现象。产液量和含水率拟合的决定系数分别为0.866和0.953、平均相对误差分别为3.05%和2.15%，说明模型具有较高精度。

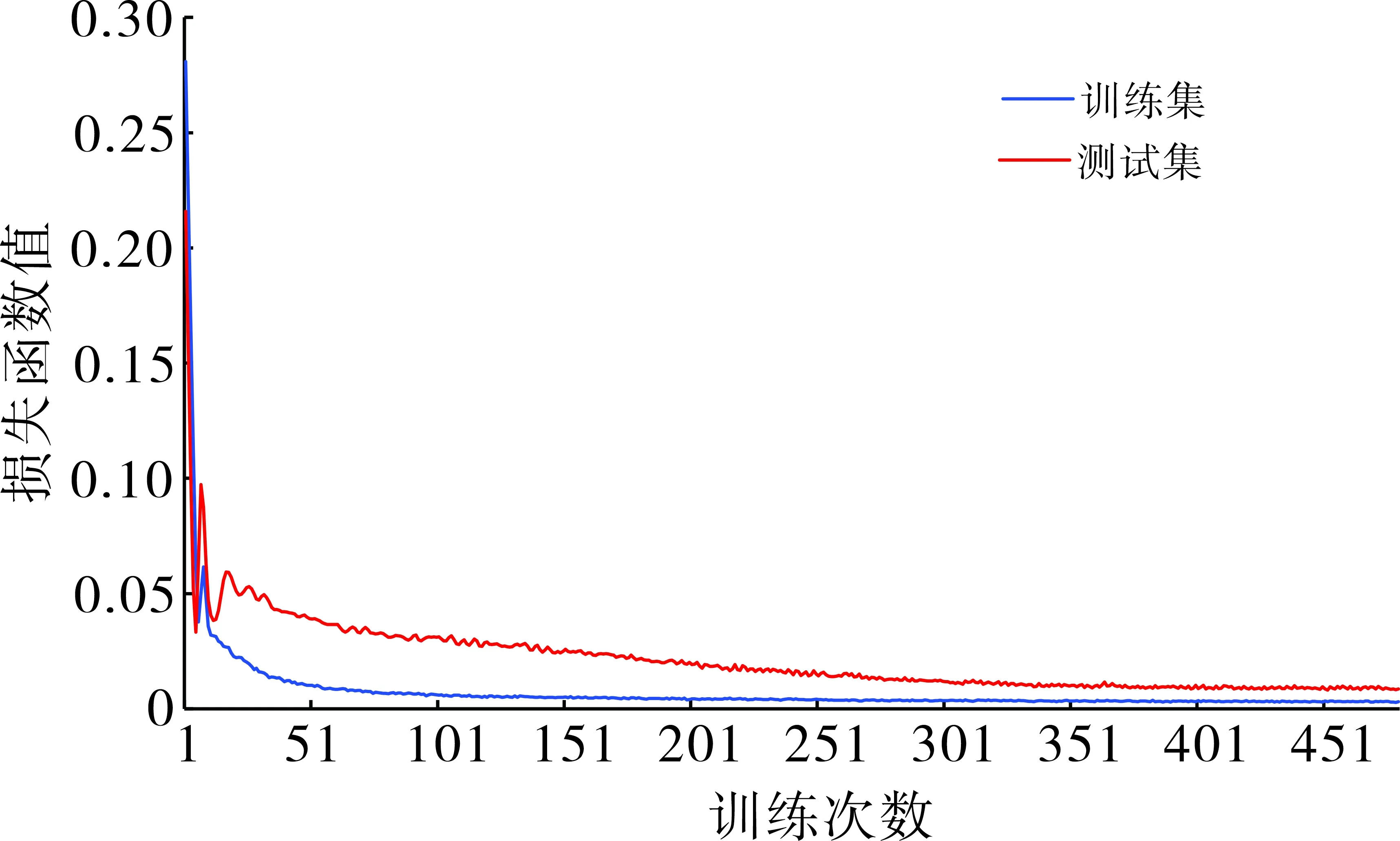
图4 B29井训练集和测试集损失函数随训练次数的变化

根据建立的长短期记忆神经网络模型，B29井产液量和含水率预测结果如图5、图6所示，产液量和含水率预测的决定系数分别为0.745和0.829，平均相对误差分别为12.68%和4.45%。从预测结果可以看出，B29井长短期记忆神经网络模型的预测结果准确掌握了该井产液量和含水率的变化趋势，部分日期的预测结果与实际结果对比，二者吻合度较高，相对误差较小(表2)。

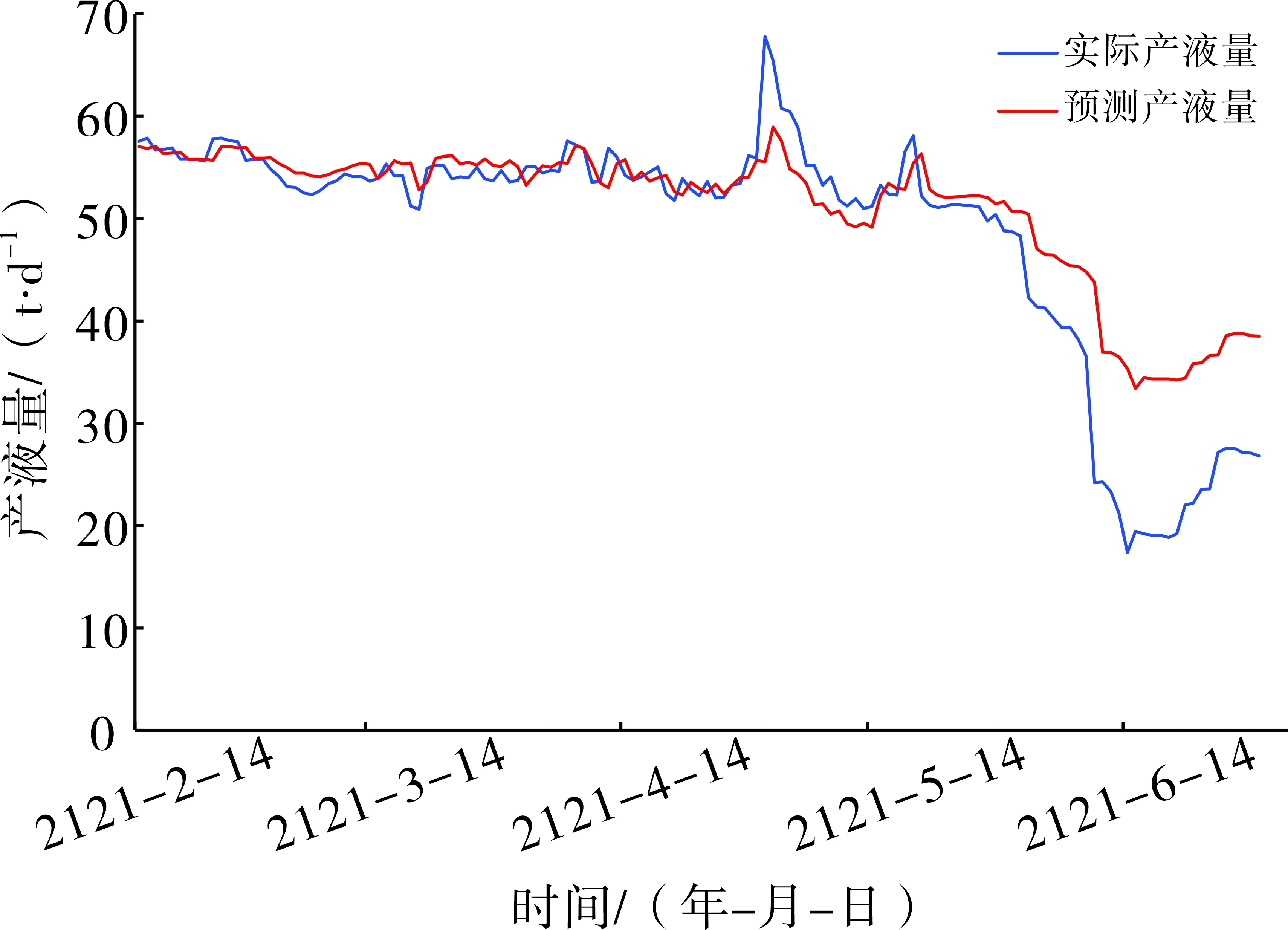
图5 B29井测试集产液量预测结果

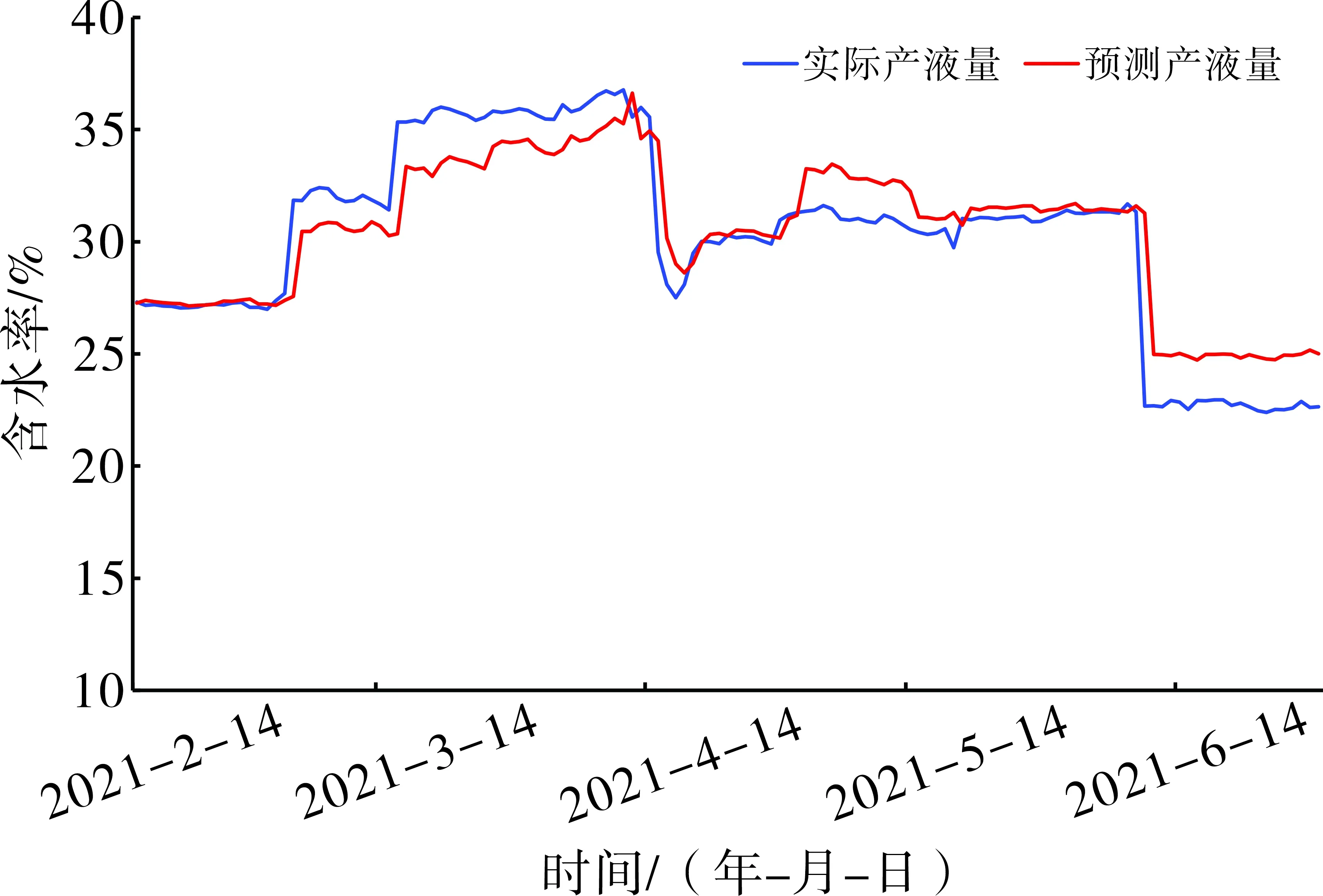
图6 B29井测试集含水率预测结果

表2 B29井产液量和含水率预测值与实际值统计

采用相同的方法对井组内其余生产井进行产液量和含水率预测，平均相对误差统计结果如图7所示。井组产液量和含水率平均误差分别为6.22%和2.97%，能够满足现场工程应用要求。利用训练好的模型，可以用于井组分层注水优化，为现场注采方案调整提供依据。

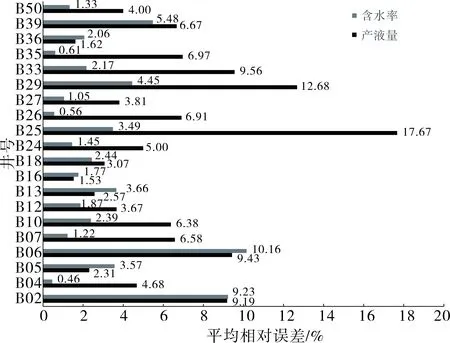
图7 井组所有生产井产液量和含水率平均相对误差统计

3 结论和建议

(1)考虑油井生产动态数据的变化趋势和前后关联性，利用现场易得到的分层注水数据以及油井产量和含水率数据，建立了一种基于长短期记忆神经网络的油井产量和含水率预测方法。

(2)现场实例应用结果表明，基于注水井分层注水量为特征的LSTM模型可以很好地预测油井产液量和含水率变化，井组产液量和含水率平均误差分别为6.22%和2.97%，预测精度能满足现场工程应用要求。

(3)基于平均不纯度减少的特征选择方法能够有效筛选出影响油井产液量和含水率的主要注水层段，有助于认识生产井与注水层段之间的相互关系，同时为降低预测模型复杂度、提高计算效率奠定基础。

(4)基于目前研究成果，可以进一步将区块中各口油井之间的相互影响引入MDI分析和LSTM模型中，以考虑油井之间的干扰影响；此外，也可将建立的方法用于油井沉没度、系统能耗、举升效率等生产指标的预测。