水滴动态疏水性的研究

郭嘉为，陈 靖，陈宗强，孔勇发

(南开大学 物理科学学院，天津 300071)

当水滴接触某一表面时，表面对水的润湿性不同,水滴与表面之间会产生不同的接触角，接触角可以反映材料的疏水性质[1]. 一些材料表面具有微纳级的结构或微粒，这使得水滴与材料的静态接触角大于150°，材料呈现出疏水性[2]. 例如，荷叶上的水能够聚成小水滴，是因为荷叶表面具有随机排列的μm尺度的精细凸起结构[3-4]. 受荷叶疏水原理启发，人工疏水性材料被制成，且已被广泛应用，例如制造自清洁材料、防腐材料、防附着材料等[5-8]. 然而这些疏水材料的制作工艺复杂，加工成本高，且无法动态调控.

2014年，H. Lhuissier等人报道了在绕水平轴快速旋转的滚筒内壁水滴可能悬浮在上升一侧的筒壁上的研究成果[9]. 该研究认为，水滴之所以不接触滚筒内壁，是因为两者之间隔有1层流动的空气膜，由于空气膜的厚度不均匀，其中的气压也不均匀，从而可以为水滴提供支持作用. 与空气接触时，水滴在表面张力的作用下可以大致维持形状. 受文献[9]启发，本文设计并研究了旋转平台的动态疏水特性. 通过控制平面的转动速度形成适当的空气膜，下落的水滴与空气膜的碰撞就会出现疏水特征. 通过理论建模分析了下落水滴与运动空气膜之间的撞击过程，给出动态疏水性产生的临界条件. 实验上通过将旋转光盘作为旋转平面，搭建实验装置并观察了水滴大小、下落高度和旋转平面转速对动态疏水性的影响，得出旋转平面出现动态疏水性的临界速率与水滴的下落高度、半径呈正相关. 与文献所述的静态疏水性表面比较，本文提出的动态疏水性实验模型具有疏水性能灵活调控的优势.

1 理论分析

1.1 空气膜支持模型

为了能够清晰地说明动态疏水性，首先分析旋转平面形成的空气薄膜对静态水滴的支持作用，之后再扩展到运动水滴对空气膜的冲击作用.

旋转平面上的水滴与空气膜的受力分析如图1所示.图1(a)中灰色部分为旋转水平面(具体实验选用光盘).V为水平面的平动速度，选取水滴中心轴所在截面进行受力分析.当水滴接触空气膜时，其下端会首先形变为近似于平面的形状，形变部分宽度为lg；形变的端点与水滴中心夹角为θ；κ为水滴表面的曲率.以水滴底部中心为原点建立正交坐标，ex和ez分别为x和z轴的单位向量.取与水滴中心等高的左侧膜上点(x0,z0)，水滴外的大气压为p0.图1(b)为水滴与空气膜接触面局部[图1(a)中红色椭圆部分]的放大图，空气膜厚度h=h(x)，图中箭头表示气体的流速，由于气体的黏滞作用，空气膜下端气流与运动平面速度相同，上端与水滴底部速度相同.

(a)受力情况

空气膜与水滴接触部分的压强为p=p(x)，对水滴接触空气膜的任一点列拉普拉斯方程有：

σ(κ0-κ)+ρg(z0-z)=p-p0,

(1)

其中，σ为水的表面张力系数，ρ为水的密度，g为重力加速度.

空气膜中的p关于x的导数满足：

(2)

其中,η为空气的黏度，q为单位时间内垂直于流速方向上单位长度的空气体积通量.

联立式(1)～(2)，得到：

(3)

(4)

(5)

式(4)可以改写为

(6)

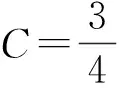
(7)

(8)

联立式(5)，(7)和(8)，解得:

(9)

积分得到空气膜对水滴竖直方向上的附加力为

(10)

其中，fz为空气膜能够提供给水滴的稳定支持力，fz与V呈正相关，注意到水滴为二维模型，fz的量纲为kg/s2.式(10)成立的条件是空气膜很薄，空气膜上端为弧度较小的曲线以及空气膜内为层流.

水滴悬停在空气膜上时，水滴底部空气膜流速和压强的数值模拟结果如图2所示，图中空气薄膜为其纵向中心截面，模拟条件为空气具有黏性，空气膜两端连通大气，且其上表面与水滴接触静止悬停，其运动速率V=0 ，下表面的运动速率V=15 m/s，与实验速率一致.

图2(a)所示的模拟结果验证了在空气膜较薄、上端弧度较小的条件下，膜中气流为流速自下而上递减的层流，只在空气膜两端厚度较大，与大气联通时出现少部分湍流. 图2(b)所示的模拟结果显示空气膜中由气体流动带来的附加压强分布，红色部分高于大气压，蓝色部分低于大气压，在气压不对称的空气膜中，附加压强关于空气膜上部的积分大于0，总体为支持力.在空气膜两端，附加压强快速降为0，这验证了产生湍流的部分气压对支持力所做贡献较小，因此忽略湍流的影响.取K=1，无量纲的空气膜厚度H、无量纲的空气膜压强P水平方向的分布图如图3所示.

(a)空气膜中的气体流速

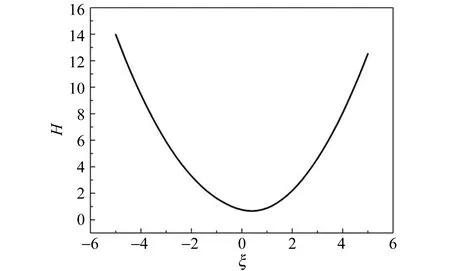
(a)H-ξ分布图

图3(a)中H图像最低点向ξ轴正方向偏移，H的不对称导致P的不对称，使得气压关于横坐标的积分大于0，这是空气膜对水滴支持力的来源，改变水平面运动速率相当于改变了支持力的大小.

1.2 水滴撞击空气膜

计算水滴撞击平面产生的最大压力，水滴为流体模型.在触碰移动平面前，水滴对空气膜的压力来源于水滴的冲力F和落到平面上水滴的重力G.

与1.1分析相似，水滴落到平面上时，与空气膜接触的部分会先产生形变，记形变部分的端点与水滴中心夹角为θ，见图1(a)，有：

(11)

(12)

(13)

实验中有hl≫R，则式(13)可近似为

(14)

解得水滴对空气膜压力最大值为

(15)

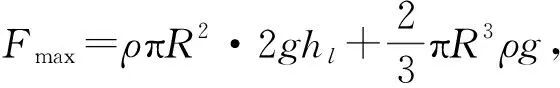
1.3 动态疏水性临界条件

当水滴接触空气膜时，先落到空气膜上的部分会在水平方向上快速扩散开，形成较薄的圆形水“饼”[10].因此实际与空气膜有相互作用的是扩散开的这部分，记这部分水“饼”的直径为D.数值模拟分析表明，空气膜很薄，其上端为弧度较小的曲线以及膜内为层流的假设基本成立.故空气膜对水滴竖直方向的支持力fz满足式(10)给出的稳定形式.分析空气膜支持力fz时选取稳态模型，针对水滴被弹起的临界情况进行分析.在水滴恰好能够被弹起的临界状态，有fz=Fmax.如果在非临界状态下水滴反弹，则F压在取到Fmax之前就已经开始减小；如果水滴接触运动平面，则“水滴底部在竖直方向上的速率为零”的稳态条件不可能达到，空气膜的稳定条件被破坏.在这2种情况下，空气膜的支持力也不是稳定值fz.因此，可以判断如果fzFmax，则水滴在空气膜支持力fz取到稳定值之前已经开始反弹.综上，临界条件可由稳态条件下的fz=Fmax给出.

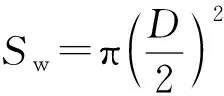
(16)

解得半径为R的水滴从高度hl自由下落到平面上且刚好能被反弹时，平面的临界运动速率为

(17)

记扩散开的水“饼”边缘的曲率半径为rΔ，则水“饼”厚度约为2rΔ.水滴接触空气膜时，已经落到空气膜上部分总体积为Vs=Vs(θ)，为

(18)

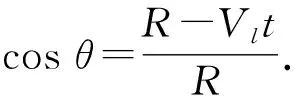
(19)

因此，有

(20)

在实验中有hl≫R，可认为水滴有一半落到空气膜上时给空气膜的压力为最大值，此时有Vlt=R，即压力取到最大值时，

(21)

水“饼”边缘的运动状况比较复杂，因此其曲率半径rΔ的具体表达式难以确定，不过可以推测出rΔ与哪些物理量有关.

(22)

再代入式(17)，得到：

(23)

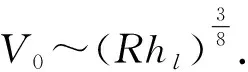
1.4 模型合理性分析

水滴落在空气膜上时，除了受到竖直方向的支持力，还有水平方向的力，这个力分为2部分：气体的黏滞力作用和气压在水平方向的作用.其中气体的黏滞力与气流同为水平方向，不影响空气膜的支持力，而气压在水平方向上的作用会引起空气膜支持力fz的微小变化.由于水滴底部的曲率，空气膜的支持力在计算时可分解为水平f1和竖直f2，则有(dfz)2=(df1)2+(df2)2，且

(24)

(25)

在前文分析中使用二维模型，选取的截面是过水滴中心的纵向x-z截面.同理，相似的分析也可以应用于垂直于平面运动方向上的其他截面，从而拓展到三维情况.设某一时刻水滴底部与空气膜接触的区域为直径D的圆,则沿平行于平面运动方向选取任一截面，此截面接触空气膜的长度d≤D,则与1.3分析类似，水滴对空气膜的最大压力在此平面的投影为

(26)

式(26)表明，只在过水滴中心的截面上有d=D，f能够取到式(16)给出的最大值.也就是说，在非水滴边缘的截面上，式(10)基本能够满足空气膜很薄，且空气膜上端为弧度较小的曲线以及空气膜内为层流的假设，fz都具有式(10)给出的类似形式.若在过中心截面上有fz≥fmax，则其他截面也满足fz≥f.过水滴中心的截面上分配了水滴最多的压力，因此，只要该截面上能够满足空气膜支持条件，水滴总体就不会接触运动平面.而在水滴边缘部分，式(10)的假设不被满足，但在水滴表面张力维持球形的作用下，越接近水滴边缘，水滴底面离旋转平面就越远，越不容易与运动平面接触.由图3(b)可知，靠近水滴边缘时空气膜中附加压强迅速接近0，不对fz产生主要贡献，对分析影响较小.

综上，过水滴中心的纵向截面部分最容易接触运动平面，选取这个典型截面给出的动态疏水性判据适用于三维水滴模型分析.

2 实验研究

2.1 实验装置

实验装置示意图如图4所示,其中酸式滴定管最小分度为0.1 mL，电机输入电压U不超过4 V，在此区间内电机转速稳定. 使用电机驱动光盘作为水平运动的平面，以数字万用表监控电机输入电压U的稳定性，标记光盘边缘一点，使用高速摄像机拍摄光盘在某一稳定电压下转10周的时间，计算得到电机的平均转速ω.图5表明，在实验输入电压范围内，ω随输入电压U的增加呈线性增加. 拟合关系为ω=kU+b,其中k=(142.8±2.4) rad/(s·V),b=(3.2±3.8) rad/s.

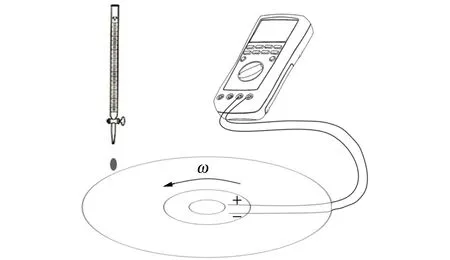
图4 实验装置示意图

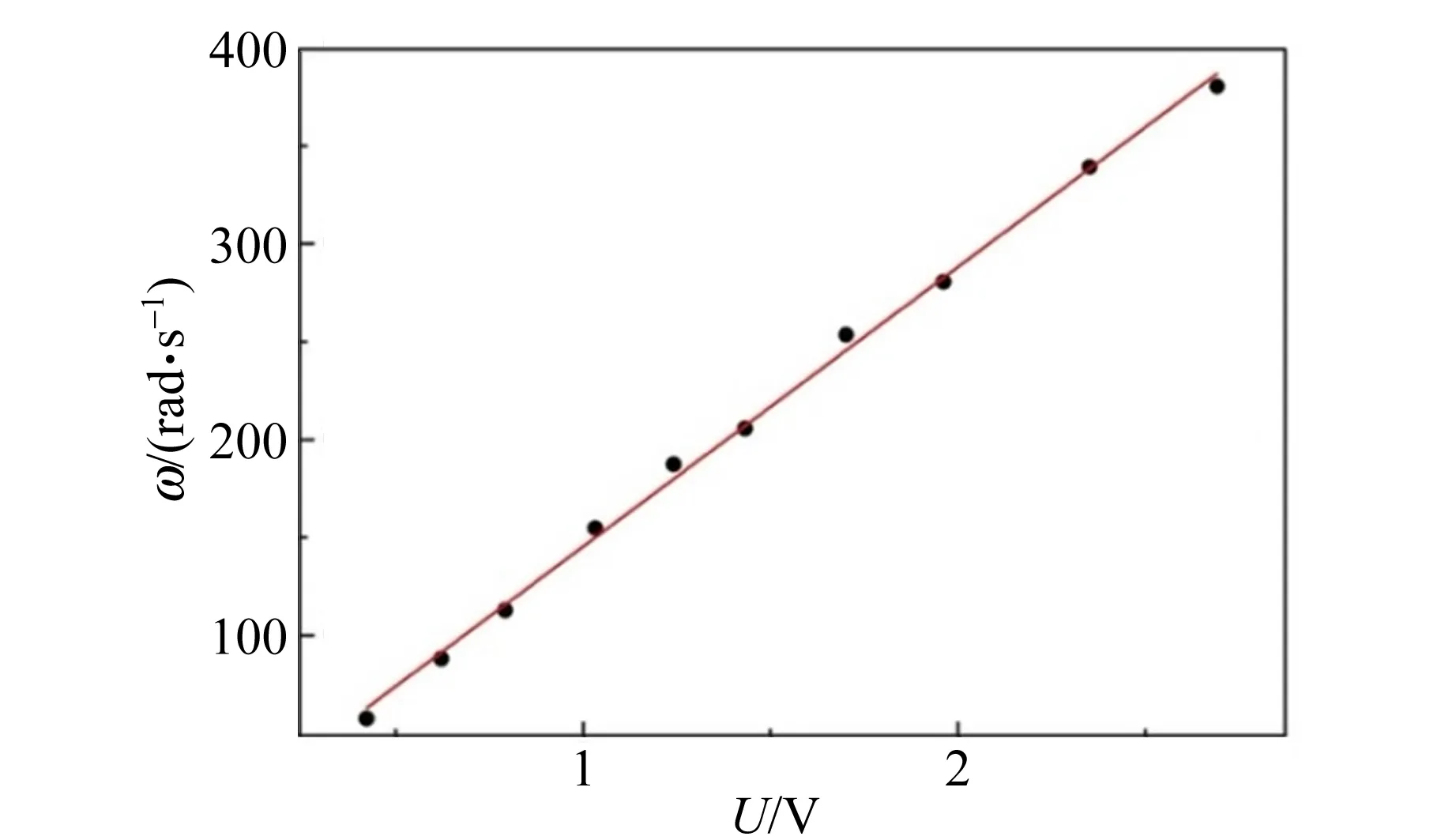
图5 驱动光盘的电机转速与输入电压的关系

实验中水滴落点到转轴距离约为5.5 cm，水滴半径约为2.5 mm，可以认为水滴尺度远小于光盘，水滴底部接触到的范围内，光盘表面平动速度均匀. 以酸式滴定管释放水滴，测量滴定管头到光盘表面的距离得到水滴下落高度hl，读取释放水滴前后酸式滴定管的读数变化，得到水滴体积，进而计算得到水滴的初始半径R.

以高速摄像机拍摄水滴接触平面的过程，观察水滴是否被反弹. 光盘表面刻痕的精度为μm量级，因此，不考虑刻痕对疏水性的影响. 如果实验观察到空气膜没能反弹水滴，则水滴接触光盘后部分破裂或者完全破裂.

2.2 实验结果

实验中使用高速摄像机拍摄不同初始条件下水滴接触平面后的状态，观察到水滴与运动平面碰撞后分为3种状态，如图6所示,h=4.250 cm. 图6(a)为水滴能够完整弹起，此时水滴与运动平面间空气膜足以支持水滴的冲击；图6(b)为水滴接触平面后，下半部分被快速扯裂(见红圈部分)，而其余部分能够反弹，此时水滴“半破裂”，对应平面运动速率在临界速率附近；图6(c)为水滴接触平面后被完全扯裂并随平面同速运动，对应平面运动速率不够高，空气膜不足以支持水滴的冲击，使得水滴与平面直接接触.

(a)水滴完整反弹(V=20.6 m/s,R=2.67 mm)

图7 不同疏水性状态下水滴的V-A散点图

实验中观察到成功反弹的水滴被弹起后获得的水平速率远小于运动平面的速率，未能成功反弹的水滴，部分或者完全与运动平面共速，这2种现象是界限分明的.因此，从实验上证明了1.4节理论模型中忽略水平方向气流作用的合理性.

将图7的坐标延伸至原点，可得水滴动态疏水性的半经验判据，如图8所示，动态疏水性可由V-A判据调控.实验结果与理论符合，可验证临界速率V0-A的半经验公式.判据表明，在固定水滴尺寸R和水滴下落高度hl的实验条件下，即A一定，则平动速率V越大，水滴越容易被反弹；在实验范围内，平动速率V和水滴下落高度hl一定，水滴的初始半径R减小时，由于Fmax与R有关，A总体会减小，则水滴越可能被反弹.

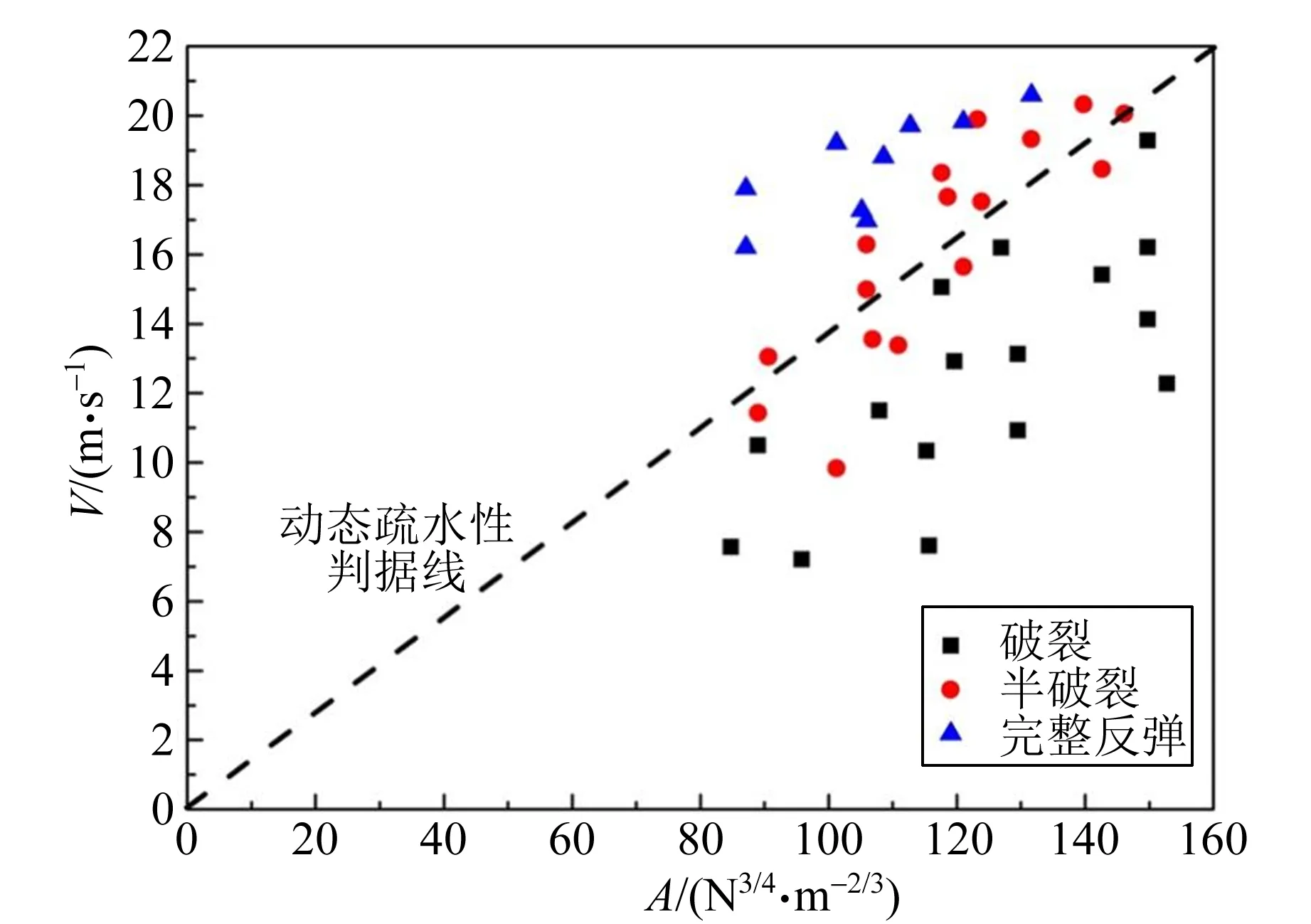
图8 呈现动态疏水性的半经验判据线

由于实验仪器的限制，平面运动速率和水滴半径可取的区间有限，这使得无法在更大范围测量.另外在水滴离平面特别近或特别远时，水滴对平面的冲击力以及空气膜的支持力可能与现有理论存在偏差，这需要根据实验结果进行修正.

3 结束语

本文证明了运动平面和落到其上的水滴之间存在空气膜，可以为水滴提供支持力，从而使得平面呈现动态疏水性.给出水滴能够被反弹的判据为空气膜提供的支持力足以抵挡水滴对空气膜的最大冲击力.同时验证了水滴自由下落到运动平面上并且刚好能被反弹时，平面的临界平动速率与水滴初始半径、水滴下落高度呈正相关关系，得到水滴疏水性的半经验判据.本实验的设计与研究为实现动态疏水性表面提供了新思路，通过调控旋转平面的转速，可以实现不同种类、不同质量和不同运动速度水滴的动态可调控疏水特性控制.实验装置设计简单、可控且易于实现，对大学本科物理实验在流体力学、超疏水材料等方面进行了有益扩展和补充.