高阶彩虹现象的观测及其色散特性研究

刘 涵，李咏璇，区艺锋，颜秉琪，苏琪淇，彭 力,2

(1.华南师范大学 物理与电信工程学院，广东 广州 510006;2.华南师大(清远)科技创新研究院有限公司，广东 清远511517)

虹与霓是大气中常见的自然现象，可以在实验室搭建装置，实现彩虹现象的再现与展示[1]，探究彩虹的偏振特性[2]. 也有文献报道液柱彩虹系统[3]、全场彩虹技术反演算法[4]等. 但目前关于3级以上彩虹的研究相对较少，对高阶彩虹现象的研究多采用单色激光进行演示[5]，而缺少对高阶虹的最小偏向角、色散规律等物理特性的研究. 高阶虹形成的本质为光的散射强度在特定角度达到极大值的现象，光线在最小偏向角附近聚集才形成了虹. 因此，最小偏向角是研究高阶虹的重要特性参量.

本文从高阶虹形成的原理出发，搭建了基于环形光屏的高阶彩虹观测装置，通过读取装置光屏上的角坐标实现最小偏向角的精确测定. 采用不同波长的激光入射，进一步探究了高阶虹的色散规律. 本设计获得2021年第7届全国大学生物理实验竞赛一等奖.

1 虹、霓及高阶虹的形成原理

虹与霓形成的光路图如图1所示. 在球形液滴中发生2次折射、1次反射后的光线会聚形成了虹，发生2次折射、2次反射后的光线会聚形成了霓.

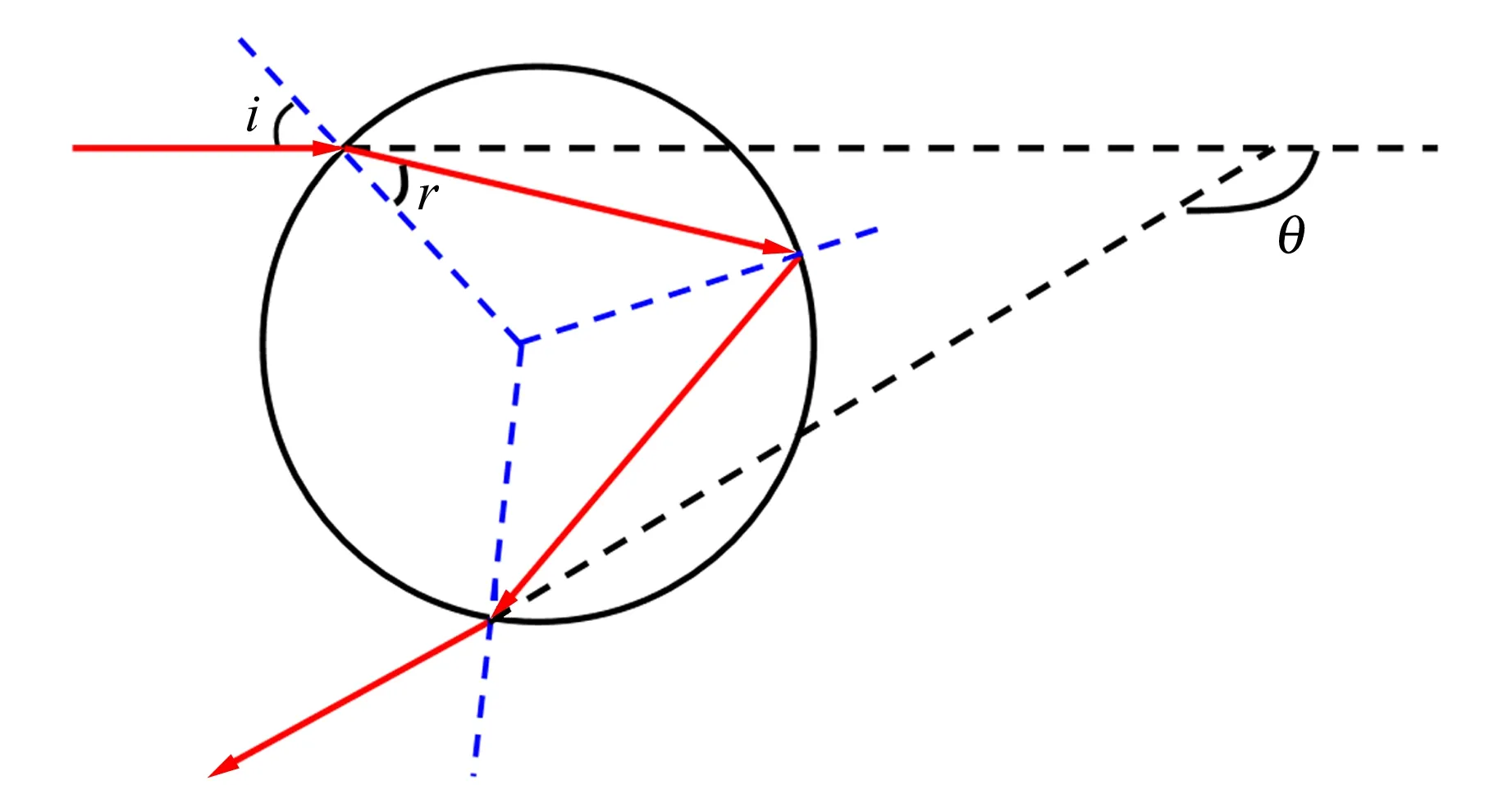
(a)虹

出射光线与入射光线的夹角即为偏向角θ.并非所有入射球形液滴的光线出射后都能形成虹，而是存在特定的最小偏向角θ0，光线在该角附近聚集即形成了虹[6].由几何关系及斯涅耳定律，可导出虹的最小偏向角为

(1)

其中，n0为空气的折射率，n为液滴的折射率.与最小偏向角θ0对应，光线入射角存在极值i0.当入射角i在i0附近变化时，θ随i变化缓慢，宏观上表现为光线聚集于θ0处，即光强在最小偏向角附近为极大值.

当入射角i从0到90°变化时，偏向角θ先减小然后增大，宏观上表现为出射光斑先向某方向缓慢移动，当i>i0时，出射光斑朝反方向移动，这是虹与霓在最小偏向角θ0附近出现的特殊现象[7].

以上讨论均基于单色光，若产生彩色的虹必须使用白光入射.根据光的色散，介质对不同波长光的折射率不同，因此不同波长光将有不同的最小偏向角θ0[8]，如图2所示.不同波长光的极值点彼此错开形成彩色的虹光带[9].

图2 虹的色散规律

光在介质中经过多次反射、折射不仅能形成二阶虹(霓)，还能形成高阶虹(图3).若光束在介质中经历了K次反射，则定义该光束形成的虹为K阶虹[10].由几何关系可得偏向角θ与入射角i、折射角r的关系为

θ=2(i-r)+K(π-2r).

(2)

由斯涅耳定律及K可计算各阶虹的理论位置.

图3 高阶虹形成的光路示意图(以K=11为例)

2 装置设计

2.1 圆球与圆柱对彩虹形状的影响

为克服自然情境中液滴非球形、不均匀等因素对高阶虹呈现效果的影响，选用了折射率n=1.51的玻璃介质进行实验，该介质更有利于定量探究.自然界中常见的虹为半圆形或拱形，实际上，若复色光正对玻璃圆球均匀照射，将会形成圆环状的彩虹.

图4(a)中，使入射平面绕直径旋转1周，光屏上将得到圆环状彩虹. 图4(b)中，使入射平面上下平移，光屏上将得到条状彩虹. 将圆球介质替换为圆柱介质，选定入射平面测量偏向角更加方便，所以采用玻璃圆柱作为实验样品.

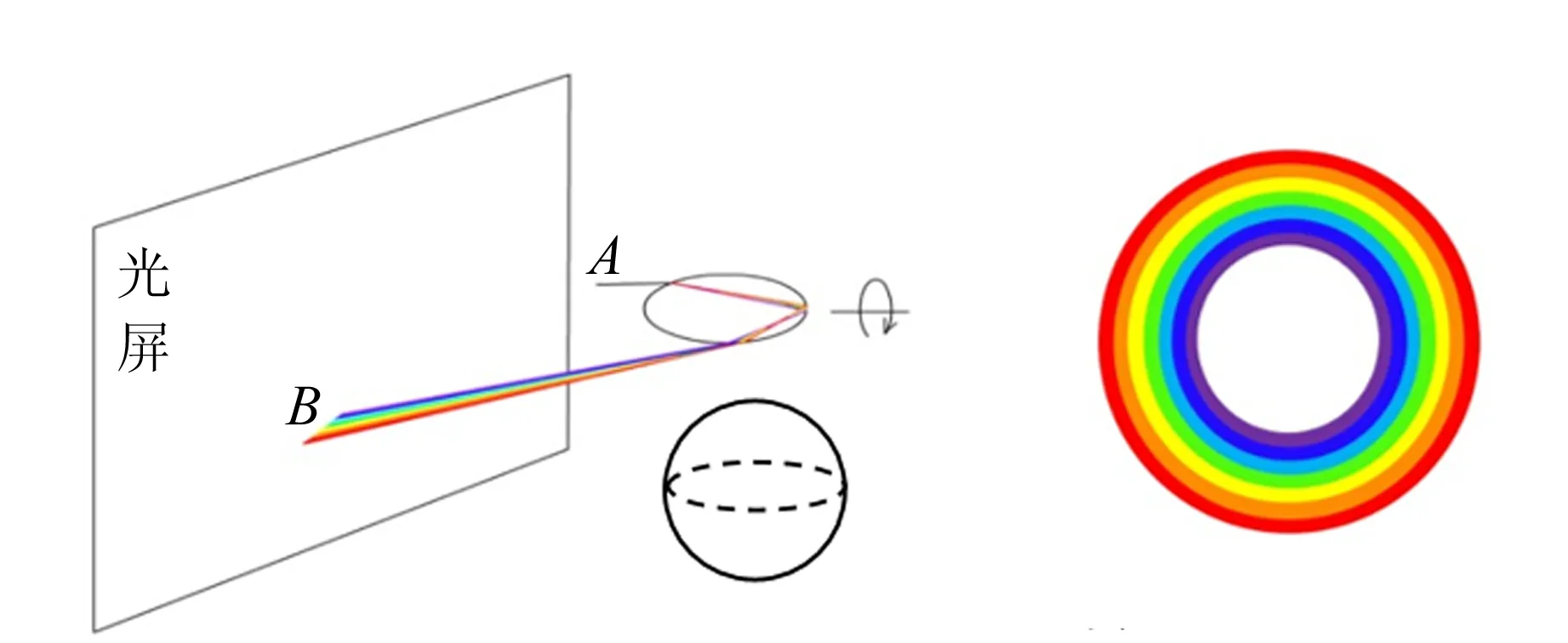
(a)圆球

2.2 高阶虹最小偏向角的测量方法

为更好地测量最小偏向角θ0，除了替换介质形状以外，还设计了基于环形光屏的测量装置，推导了所设计环形光屏上的角坐标φ与待测偏向角θ之间的关系式.装置结构如图5所示.

图5 环形光屏观测装置结构示意图

设环形光屏的半径为R，圆柱介质的半径为a.入射光线与圆柱横截面直径方向之间的距离为b.设介质中光线出射点到圆心的半径与水平方向的夹角为φ′，光屏成像点和圆心的连线与出射光线的夹角为ξ，光屏上成像点的角坐标为φ.由几何关系得:

θ-φ′=i+2mπ,

(3)

φ-φ′=i-ξ,

(4)

其中m为整数.在折射率确定时，各阶虹有唯一确定的m使得偏向角θ在0°～360°之间.

在图5含有ξ的三角形中，由正弦定理得:

(5)

联立式(3)～(5)，得

(6)

由式(6)可知，只需读出各阶虹在光屏上的角坐标读数φ，即可求得偏向角θ.

2.3 实验平台的搭建

实验装置如图6所示，装置主要由复色光系统、观测与读数系统、激光器3部分组成.在进行高阶虹观测及最小偏向角测量实验时，主要用到前2部分.

1)装置左侧为复色光系统，调节可移动底座使复色光经透镜准直后变为平行光.透镜后配备了光阑可获得不同尺寸的平行光束.底座下面安装游标卡尺，通过读取底座滑动前后的刻度，可以获得参量b，结合柱体半径a可得入射角i.

2)装置右侧为观测与读数系统.a=40 mm的圆柱形介质置于底部圆盘中央，确保二者中心转轴重合. 圆盘四周是标有0°～360°刻度的环形光屏.光屏左侧的开口用以通过平行光束. 在光屏上可清晰观测高阶虹，读出各阶虹的角坐标.

图6 观测高阶虹的实验装置示意图

当进行虹霓现象色散规律的探究实验时，将载物台上的复色光源、透镜和光阑取下，直接放置激光器，适当调整激光器的方位，确保激光光路通过圆盘0°-180°水平线.

3 实验结果与探讨

3.1 虹与霓现象的复现

实验模拟了太阳光照在球形液滴上产生的虹与霓现象. 在圆盘中心放置玻璃球，调节光源、透镜、光阑、介质等高共轴. 调节透镜的位置，使出射光为平行光. 调节光阑的宽度，使平行光束能够完整照射整个玻璃球，即玻璃球在平行光束范围内.

对于本实验装置，玻璃球的直径为70 mm，因此光阑的宽度设置为70 mm. 在光屏上观察到的实验现象如图7所示.

图7中所观察到的彩色圆弧为虹，在外侧光强稍弱的彩色条纹为霓.两者色彩顺序相反，前者为外红内紫，后者为外紫内红，实验结果与理论相符. 由于受到光屏尺寸的限制，光屏上只能呈现部分霓. 由图7可见，在当前情况下测出空间中的最小偏向角比较困难.

3.2 高阶虹观测与角坐标测量

根据前文所述的角度测量方法，计算出前6阶虹的理论角坐标位置如图8所示.

图8 高阶虹的角坐标理论位置

使用如图6所示的实验装置，进行高阶虹角坐标测量. 调节光阑宽度，使准直后的平行光照射圆柱的上半部分，观察现象并读数. 由于光强随着阶次增加逐渐减弱，为提高反射率，在圆柱体介质第一次发生反射的位置贴半透半反膜，实验现象如图9～10所示.

图9 高阶虹现象

(a)K=1 (b)K=2 (c)K=3

可见，各阶虹分布在光屏的不同位置上，随着阶数增加，光强逐渐减弱. 读取光屏上虹出现的位置，将其与理论值对比，如图11所示.

图11 高阶虹的角坐标实验值与理论对比

由图11可知，实验结果与理论值符合得较好.由式(1)可知，最小偏向角θ0与折射率n有关，θ0与其角坐标φ0的关系由式(6)确定.推导出不同折射率n下的角坐标φ0表达式[见下文式(8)]，即可在一定条件下由实验所得的角坐标φ0得到介质的折射率n.

3.3 虹与霓的色散规律探究——不同波长条件下虹与霓的偏向角随入射角的变化

激光的单色性较好，选用波长分别为λred=650.0 nm，λgreen=526.8 nm，λblue=418.8 nm的激光来探究虹与霓的色散规律. 光屏上激光光斑的尺寸如表1所示(z=76 cm).

表1 光屏上激光光斑的半径

将底座上的复色光源、透镜和光阑取下，放置蓝色激光器，确保激光光路通过圆盘0°-180°水平线. 缓缓推动底座，使激光入射角i从0°到90°变化，如图12所示.

图12 使用单色激光照射圆柱

观察光线在圆柱介质内经过1次反射后出射的光斑在环形光屏移动的轨迹和最小偏向角.读取底座下游标卡尺的读数，根据图5，入射角i与参量b的对应关系为

(7)

参量b每改变5 mm记录虹在光屏上对应的角坐标φ.再根据式(6)，由角坐标φ即可得到偏向角θ.换用红色、绿色激光重复上述实验.

根据介质对应波长的折射率，可以计算不同入射角i对应的偏向角θ的理论值，绘制理论曲线.实验结果与理论曲线对比，如图13所示.图13中的蓝色实验点整体处于最上方，红色实验点整体处于最下方，而且实验点与理论曲线符合得较好.

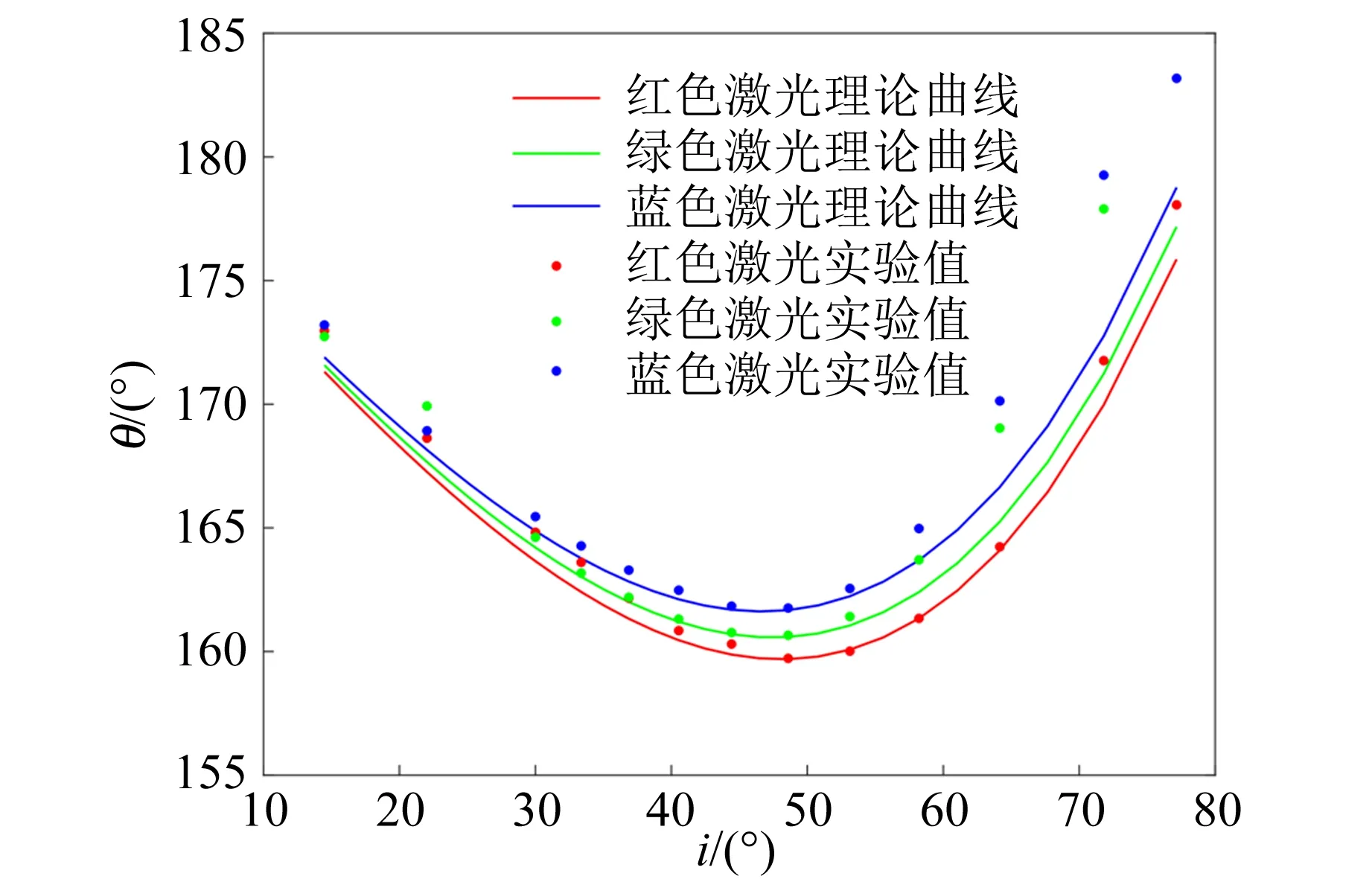
图13 虹的色散规律探究实验结果

同时，不同波长光的最小偏向角θ0不同.在入射角i比较小时，不同波长光的偏向角θ差异不大，曲线几乎重合，当逐渐接近最小偏向角θ0位置时，偏向角θ差异变大，曲线开始分开，极值点彼此错开，形成虹光带.

同理，观察经过2次反射后出射的光斑在环形光屏移动的轨迹，探究霓的色散规律，实验结果与理论曲线对比如图14所示.图14表明:霓同样也是在极值点附近曲线差距较大，两边差距较小.这解释了为什么当偏向角θ比较小时不能观察到虹，只有在特定的角度才能够观察到虹现象.

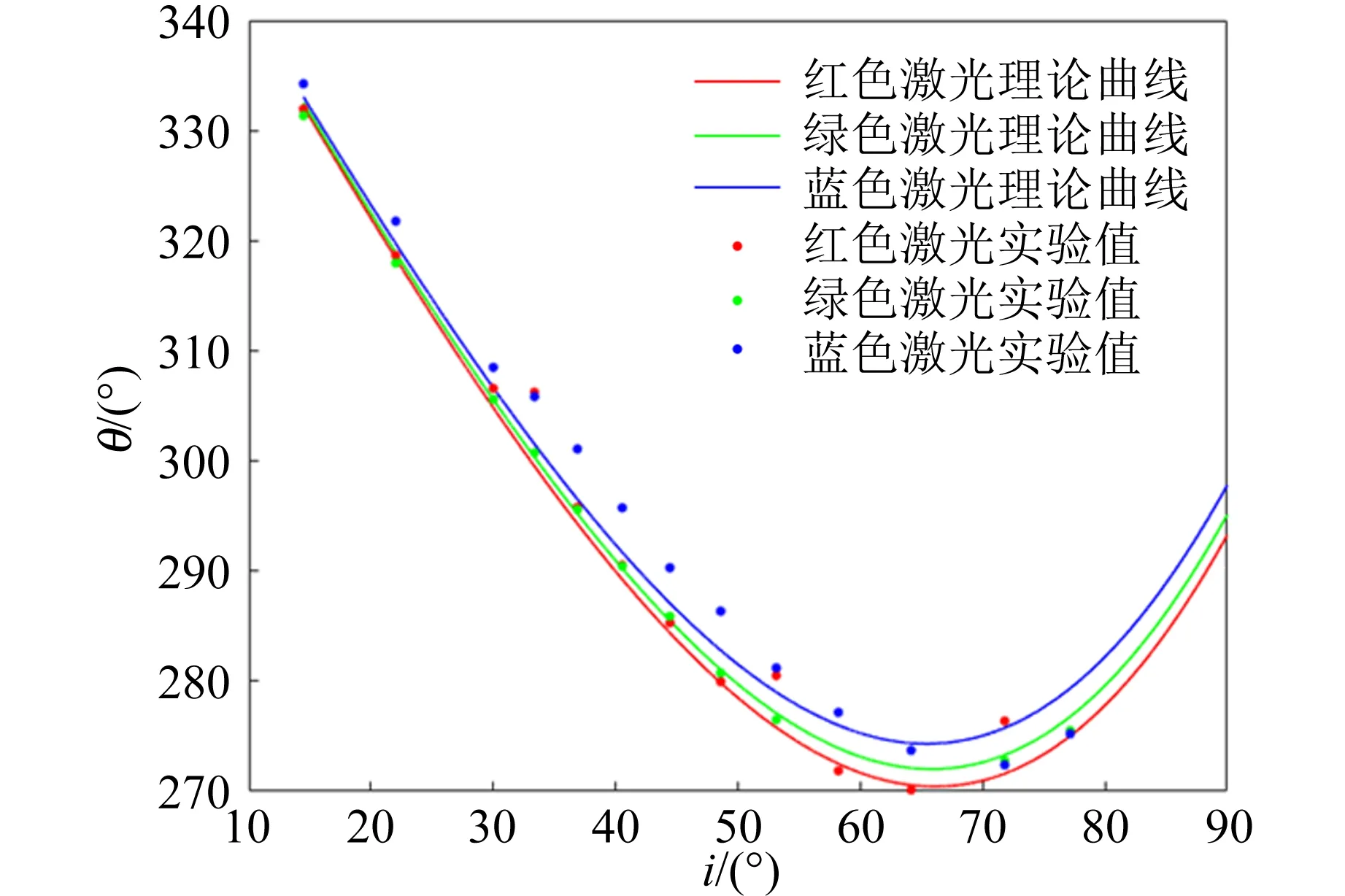
图14 霓的色散规律探究实验结果

对实验数据进行拟合，找到极值点，得到虹与霓的最小偏向角θ0，实验结果如表2所示.

表2 用激光器测量虹与霓的最小偏向角

4 应用拓展——利用高阶虹角坐标测量介质的折射率

在完成上述实验的基础上，本装置能够根据高阶虹的位置测定介质的折射率n.由于偏向角θ与折射率n有关，结合式(6)，可计算不同折射率n下各阶虹的角坐标φ，可得各阶虹出现的角坐标φ与折射率n的变化关系.

记各阶虹最小偏向角θ0对应的入射角为i0、折射角为r0.圆柱介质的半径a与环形光屏的半径R之比为倍率M，本实验装置M=0.226.记x0=sini0，y0=sinr0.由几何关系及斯涅耳公式推导出K=1～4阶虹对应的x0和y0为

结合式(2)和式(6)，得K=1～4阶角坐标为

(8)

取折射率n=1.30～1.50，绘制1～4阶虹出现的角坐标φ与折射率n的变化，如图15所示.由图15可得，角坐标φ随折射率n单调变化，因此，如果某圆柱形介质的折射率n未知，在实验测出各阶虹的角坐标φ的情况下，由图15或根据式(8)可以求出K=1～4阶虹分别对应的折射率n，求平均值作为折射率的测量结果.

(a)K=1 (b)K=2

举例:在某次实验中，圆柱形介质的折射率n未知，测出光屏上出现高阶虹的角坐标,由式(8)得到K=1～4对应的折射率,如表3所示.

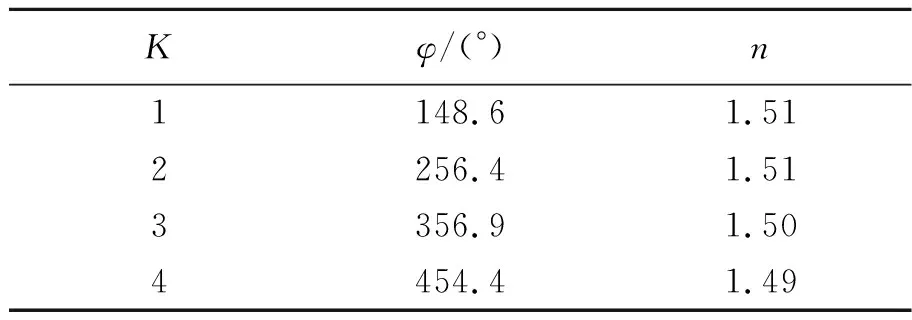
表3 由光屏上高阶虹的角坐标计算的折射率

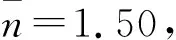
5 结束语

设计了高阶彩虹现象的综合探究装置，采用不同波长的激光入射，研究了虹与霓的色散规律，设计了利用高阶虹的角坐标测定介质折射率的方法. 将该装置引入中学或者大学物理教学中，可以为彩虹光学现象的研究提供实验平台. 该实验不仅可以激发学生的学习兴趣，引导学生探索自然界中的物理现象，还可以提高学生的动手实践能力，培养学生的创新精神，加深学生对大气光学现象的理解.