铅笔画出的电阻
——简单纸基柔性电子元件的性质探究
汪隽琪,周惠君,王寅龙
(南京大学 物理学院,江苏 南京 210093)
近年来随着可穿戴电子设备发展,柔性电器件因灵活、轻薄、便携等优点受到广泛关注. 目前,柔性电子器件的制作方法有使用复合材料体系制作[1]和通过液态金属印刷方法构建[2]等,这些方法相对复杂且成本较高. 而铅笔作为广泛使用的书写工具,具有获取方式简单,成本低的优点,铅笔芯中的主要成分为石墨,其性质稳定,画在纸上留下的痕迹能够实现柔性电子器件相关功能.
由于石墨电导率比金属低,因此在纸基电子器件中难以起到导线的作用,但因其具有压阻效应等性质,可以被制成各类电子器件[3-5]. 铅笔画出的痕迹可以作为廉价的、易于获取的电阻器. 作为电阻器,需要较为精确地控制画出的导线的电阻值,本文探究了画出的电阻与痕迹的几何参量(长与宽)、划线次数、环境温度以及纸张基底对铅笔痕迹阻值的影响,测试了铅笔导线电阻在反复弯曲后的变化情况. 并且在考虑纸张粗糙度对铅笔磨损的影响下,使用渗流模型在理论上建立了合理的半定量模型,解释了纸张基底对铅笔痕迹阻值的影响.
1 理论解释
1.1 划线模型
由于单次划线铅笔磨屑量较少,且受施力大小等因素影响较大,所以需要考虑在第1次涂抹所留痕迹上进行多次涂抹后阻值的变化,基于此考虑构建划线相关理论.
划线模型有2个基本假设:1)一次划线后铅笔磨屑能够形成厚度为h的涂层;2)划过原有涂层蹭掉的铅笔磨屑比例为r. 根据这2个假设建立差分关系:Δt=h-rt,将其连续化,得到厚度与划线次数的关系为
该曲线图像如图1所示,其中h=2 000 nm,r=0.3,随着划线次数的增加,h-1(正比于电阻)迅速减小并趋于稳定.
由于各种原因,划线过程中r和h不能保证完全不变,而是具有一定的分布,这就导致最终厚度趋于稳定时,在平衡位置附近有小的波动.取均匀分布,计算机模拟结果如图2所示,相关参量的期望值E(h)=2 000 nm,E(r)=0.3,h分布的半宽度dh=500 nm,r分布的半宽度为dr=0.05,测得的电阻随划线次数的增加应该遵循:
(1)
实验部分将会验证该规律,同时对该规律为后文实验探究提供了有效的控制变量的手段.

图1 厚度与划线次数关系
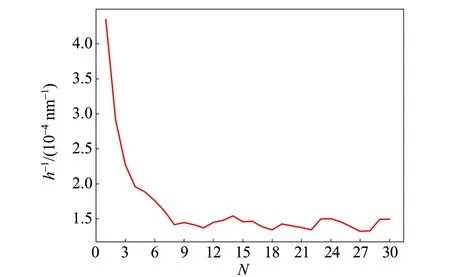
图2 计算机模拟结果
1.2 渗流模型
铅笔粉末由粘土和石墨粉末构成,作为基底的纸张具有一定的微观结构,所以画在纸张上的铅笔痕迹并不能当作金属固体,其表现出的电阻率也不是常量.电流流过铅笔磨损下来附着在纸上的石墨颗粒的过程,类似于水渗透砂石的过程,石墨颗粒类似砂石中可以被水通过的缝隙,能够使得载流子定向迁移,而粘土和纸张上凹凸不平的结构产生的无法连通的空隙就充当了砂石.
在此模型中,本质上是未连通区域、石墨颗粒和粘土颗粒三介质问题,可以简单地使用直接测量铅笔芯的电导率,而非石墨的电导率.将石墨颗粒和粘土颗粒合并为1个对象即铅笔磨屑,将问题简化为基本的二维渗流问题,如图3所示.
对于一般二元混合物的渗流问题,McLachlan给出了混合物电导率和组分的体积分数以及2种组分的电导率之间的关系[6]:
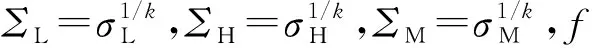

(a)连通概率较低
对于本文考虑的问题,空隙为电导率较低的组分,其电导率为0,σH为铅笔芯的电导率.化简可以得到
(2)
对于二维渗流模型,fc=1/2,f为电导率较低的组分体积分数,即空隙数占总键数的比例,统计上来讲有
f=1-P,
(3)
其中,P为连通概率.将纸张视为二维格点(图4),在每个格点上赋予纸张高度,当该点处覆盖的铅笔磨屑厚度超过相邻两格点纸张高度差时即可连通.
为了计算出概率P,假设铅笔磨屑在每一格点上附着的厚度相同,纸张每一格点的高度遵循高斯分布.该假设下连通概率为
(4)
其中,t为铅笔磨屑厚度,sd为纸张高度高斯分布标准差(表征纸张的粗糙度).误差函数


图4 纸张格点化示意图(导通判据为t≥|h2-h1|)
在其他条件相同的情况下探究纸张粗糙度对电阻的影响,纸张粗糙度更大,铅笔磨损量更大,形成的厚度也更大.绝对光滑的纸张无法附着铅笔磨屑,非常粗糙的纸张对铅笔磨损极大,使得纸张粗糙表面完全被铅笔磨屑覆盖,从而导致最后铅笔痕迹厚度与纸张粗糙度无关,基于以上分析给出厚度与纸张粗糙度的关系为
t=t0(1-e-sd/s),
(5)
其中,t0为与纸张粗糙度无关的最大磨损厚度,s为引入的常量.
由式(2)~(5)和电阻公式可以给出电阻与纸张粗糙度的关系为
(6)
代入参考数值得到电阻随粗糙度变化曲线如图5所示.
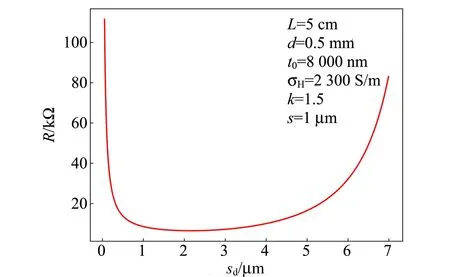
图5 铅笔痕迹电阻随纸张粗糙度的变化
2 实验探究
2.1 实验方法
实验仪器:数字万用表(UT890C+型)、中华牌101高级绘图铅笔、数显恒温水浴锅、测温温差电偶、温度湿度计、刻度尺以及其他辅助用品.
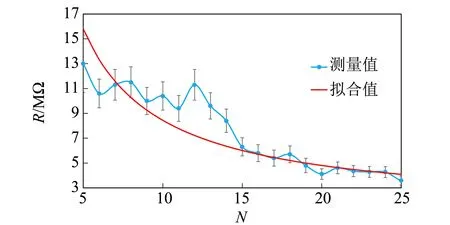
待测铅笔痕迹在确定线长、线宽条件下反复涂抹至阻值几乎不再变化时,记录该条件下的阻值,阻值可通过万用表欧姆档直接测量. 实验过程中监控温度湿度计保证实验温度湿度保持不变. 实验结果如图6和表1所示.
(a)2H
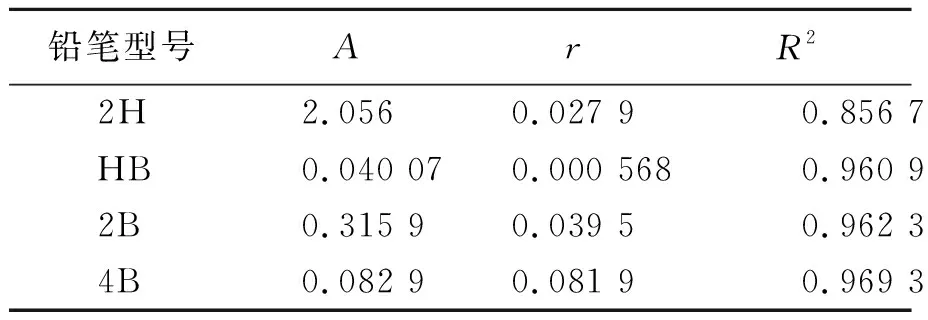
表1 式(1)实验拟合与理论公式结果
2.2 铅笔痕迹电阻的固体电阻定律的探究
固体电阻定律为:
(7)
其中,l为长度,d为宽度,t为厚度.改变铅笔痕迹的长度和宽度,痕迹导线仍然满足固体电阻定律,即电阻与长度成正比,与宽度成反比,如图7所示.
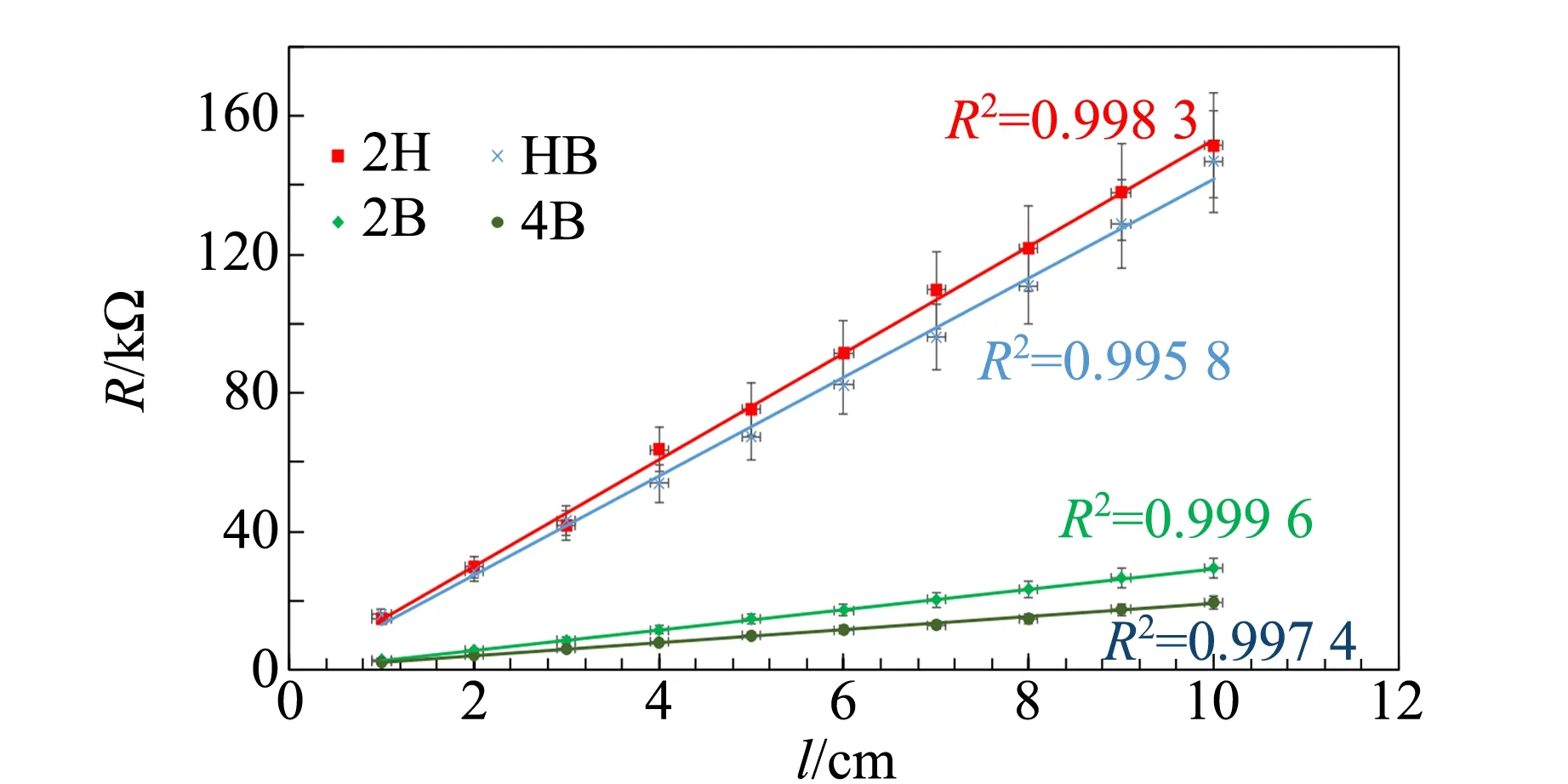
(a) 铅笔痕迹电阻随长度变化
2.3 铅笔痕迹电阻与温度的关系
将一定长度和宽度的纸基铅笔电阻放在干燥容器中,电极与数字万用表欧姆档相连,容器留小孔置于数显恒温水浴锅中,将温差电偶与电阻置于容器中同处位置,随着温度的升高,每隔一段时间记录温度与阻值. 结果如图8所示,电阻随温度的上升而下降,这与石墨的导电特性有关(不同于具有正温度系数的金属,铅笔粉末的导电部分实质是石墨).

(a) 2B
2.4 铅笔痕迹电阻与纸张粗糙度的关系
由于纸张粗糙度难以测量,选用了4种粗糙度差异明显的纸张,按光滑到粗糙依次为:铜版纸、国誉牌A4拍纸本纸、得力牌A4打印纸以及牛皮纸. 相同环境条件下,显微镜下纸的结构如图9所示.

(a) 牛皮纸 (b) 得力牌A4打印纸
对于同一铅笔,在4种纸上涂抹相同尺寸的痕迹,重复3次实验,每个电阻测量4次,测量数据如表2所示,可知电阻随着纸张粗糙度的变化,先下降后上升,符合理论分析. 这意味着存在最佳粗糙度的纸张,在痕迹长度与宽度相同的条件下,重复划线直至稳定时电阻有最小值.

表2 不同铅笔在粗糙度不同的纸张上稳定时单位宽度的阻值
2.5 重复弯曲对于铅笔画出导线电阻的影响
对于柔性电子器件,在多次弯曲后的性能变化是值得关注的. 通过将画有铅笔导线电阻的纸张包裹在圆柱上实现控制弯曲程度的方式,使用国誉牌牌纸本纸张作为衬底,使用4B,2B,HB,2H型号的铅笔. 每张纸上有3个相同型号铅笔绘制的电阻导线,共弯曲200次,前100次中,每反复弯曲20次测量一次电阻,后100次中,只记录结束时的电阻,结果如表3所示.

表3 不同铅笔在相同条件下反复弯曲后阻值的变化
从结果可以发现,对于重复弯曲对铅笔导线电阻的影响随机性较大,在前100次阻值并没有表现出随弯曲次数的增加有规律地变化,但在进行200次弯曲后相对初始值均有不同程度的增加,这是由于石墨附着在纸张上的结构反复弯曲,产生疲劳效应最后被破坏的结果. 实验结果可以发现硬度最高的2H型号铅笔绘制的导线反复弯曲后阻值更加稳定,这可能与铅笔的粘土含量有关,因此推断适量的粘土含量有助于稳定附着在纸张上石墨的结构.
3 结 论
本文利用铅笔在纸上涂抹痕迹,构造了简单的纸基柔性电阻器,研究了在第一次产生痕迹上反复涂抹后阻值随涂抹次数的变化,得到了电阻器阻值随涂抹次数增加迅速下降并在稳定值附近波动的结果. 利用控制变量法进一步研究阻值与痕迹的长度和宽度的关系,结果符合固体电阻定律. 本文从理论上分析了铅笔痕迹阻值随基底纸张粗糙度的增大而先下降后增大,并从实验上验证了这一结论. 最后,测试了纸基柔性电阻器在反复弯曲下的性能,发现2H型号铅笔绘制的电阻在测试下表现出更好的性能.

