气液联合式碎石器气穴控制分析

毛文亮， 赵彦军， 柴红强, 李广东

(1.甘肃机电职业技术学院 智能控制学院， 甘肃 天水 741001； 2.兰州理工大学 能源与动力工程学院， 甘肃 兰州 730050；3.兰州兰石石油装备工程股份有限公司 钻采装备研究院， 甘肃 兰州 730300)

引言

作为液压传动装置的一种执行元件，气液联合式碎石器经常与挖掘机、装载机以及其他行走式液压工程机械配套，已成为挖掘机不可或缺的附属机具，广泛应用于采矿工程、建筑行业、冶金行业等领域[1-2]。

气穴现象是流体机械中常见的一种既隐秘且有害的瞬态过程，气穴的出现特别是严重气穴的发生会导致局部低压处形成大量气泡。气泡受到挤压后瞬间破灭，产生强烈的液压冲击以及高温，同时油液中空气的分离致使油液酸化，从而对金属零件表面产生化学腐蚀。长此以往，金属表面会受到侵蚀和剥落，或者出现海绵状的小洞穴，即出现气蚀。气蚀的产生不仅会污染系统工作介质，增加了产品工作的潜在隐患和薄弱环节，降低了产品寿命，甚至导致整个系统无法正常工作[3-5]。

近些年对于气液联合式碎石器的研究主要集中在输出特性分析、控制策略探索以及性能测试查究等方面。其中，影响较大的研究是在考虑岩石性能的条件下建立基于冲击力学及波动力学的系统仿真模型，以优化某方面性能为目标，研究对应参数对其影响规律[6-8]。李晓豁等[9-10]利用果蝇算法对碎石器进行故障诊断，建立了系统输入故障征兆与输出故障原因间的映射，同时利用MATLAB软件编程进行仿真实验。吴万荣等[11]提出了一种基于压力反馈原理的新型能频独立调节碎石器，从而实现了输出工作参数的独立控制。叶小华等[12]结合虚拟仪器技术的独特优势成功研制出了基于虚拟仪器的测试系统，从而实现了碎石器的性能测试。在此基础上，刘忠等[13]通过分析某一典型冲击机械的控制系统原理,设计了一种工作性能参数测试系统。

为实现可靠性增长的目的，需要挖掘碎石器使用中出现的潜在隐患和薄弱环节。气蚀作为影响冲击振动机械可靠性设计的重要内容，然而公开出版的相关研究却寥寥无几。邓龙等[14]通过建立的联合仿真模型确定了碎石器工作过程中相关零件产生气蚀的根本原因，同时将仿真结果与实际工程中出现的气蚀真相进行了对比，可是，该研究并没有明确提出消除气穴同时解决气蚀的相关方案。另外，马富银等[15]利用滑移网格简单描述了活塞周围的内流场，但该研究甚至没有提到碎石器内部出现气穴的可能性。

鉴于此，本研究在建立基本控制方程及质量输运方程的基础上，根据碎石器结构原理同时参考主机液压系统管路布置搭建了包含动力系统及控制系统的整机AMESim仿真模型。之后基于影响气穴的参数类型及对应取值范围设计了正交试验方案，在此基础上进行了仿真分析并获得了提高活塞后腔最低压力的最优水平组合。最后，针对集中参数模型无法反映流体质点运动空间的不足，进行了CFD模型与AMESim输出最优参数组合的联合仿真，并和AMESim模拟结果进行了对比。

1 数学模型建立

1.1 基本控制方程

由于碎石器工况条件的特殊性及活塞与阀芯速度的匹配性等导致相应容腔内的压力急剧降低，甚至低于空气分离压，这样，液压油为含有大量空气的混合介质。假定其中液相与气相充分混合，同时忽略相间滑移作用及油温变化，故只需求解混合相的连续性方程及动量方程，则连续性方程为：

(1)

式中,ρm—— 混合相平均密度

i—— 流动维数

t—— 时间

动量方程为：

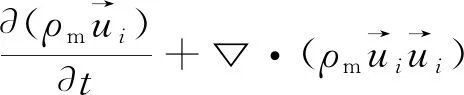
(2)

式中，p—— 静压力

μm—— 混合相动力黏度

对应混合相的密度及黏度方程如下：

(3)

μm=αlμl+αfμf+(1-αl-αf)μv

(4)

式中，αf,αl—— 自由空气及油液体积分数

ρf,ρl,ρv—— 自由空气、油液及油蒸气的密度

ul,μf,μv—— 油液、自由空气及油蒸气的绝对黏度

1.2 气穴流质量输运方程

气穴模型能够利用不同的物理模型来预测流体系统的气穴与气蚀现象。本研究采用平衡溶解气体模型，该模型求解以下控制方程：

(5)

(6)

gf+gd=const

(7)

式中,Df—— 蒸气扩散率

Dgd—— 溶解气体扩散率

Cc—— 冷凝系数

Ce—— 蒸发系数

fv—— 蒸气质量分数

gd，gf—— 溶解气体与自由空气质量分数

gdequil，gdequilref—— 参考压力及压力p对应平衡溶解气体质量分数

pv，pgdequilref—— 饱和蒸气压与参考压力

Rc，Re—— 蒸气压缩与生成率

2 仿真模型及正交试验方案

2.1 AMESim仿真模型

碎石器作为一种精密元件，其内流道形状多变、结构复杂；另外，表征流动特性的相关物理量变化剧烈且相互耦合。假如全面反映研究对象的细节特征，不仅影响求解精度，甚至可能出现无法求解的情形。因此，基于研究的主要目标进行合理假设，从而实现既能够准确反映实际的物理过程，也能够达到快速计算的目的。具体假设条件如下：

(1) 不考虑油液属性受温度及压力变化的影响；

(2) 采用定量泵进行供液；

(3) 根据研究目标，不考虑油液中瞬时压力波的传递时间；

(4) 碎石器内部与油液相互作用的零件视为不变形的绝对刚体，其余系统部件按实际设置；

(5) 高压蓄能器及氮气腔的气体变化状态视为绝热过程；

(6) 蓄能器隔膜质量及变形视为理想状态。

气液联合式碎石器对应仿真模型主要包括主运动部件及内部油道建模两部分。对于主运动部件中的活塞及阀芯，需要根据对应结构同时考虑与其配合的相关油口进行建模；对于高压蓄能器则直接调用标准液压库中对应元件，同时根据实际情况赋予进口阻尼子模型。

内部油道的建模不仅需要考虑局部阻尼形状还要对沿程损失进行定量计算，因此管道子模型及液压阻尼元件的准确选取就显得意义重大。综合以上几点可得碎石器的AMESim仿真模型。在此基础上参考主机液压系统管路布置，搭建包含动力系统以及控制系统的整机AMESim仿真模型，见图1。

需要说明的是：图1中下部为活塞AMESim模型，上部为阀芯AMESim模型，其余为内部油道及供液系统对应的模型；内部流道中容积变化较大的容腔全部采用可变容积元件来表征；为了模拟回油背压，在换向阀回油侧及系统回油通道分别添加了可变及固定阻尼孔。

图1 气液联合式碎石器整机AMESim仿真模型

据以上分析，结合碎石器结构参数及工作参数，列出整机仿真模型的主要参数，见表1。

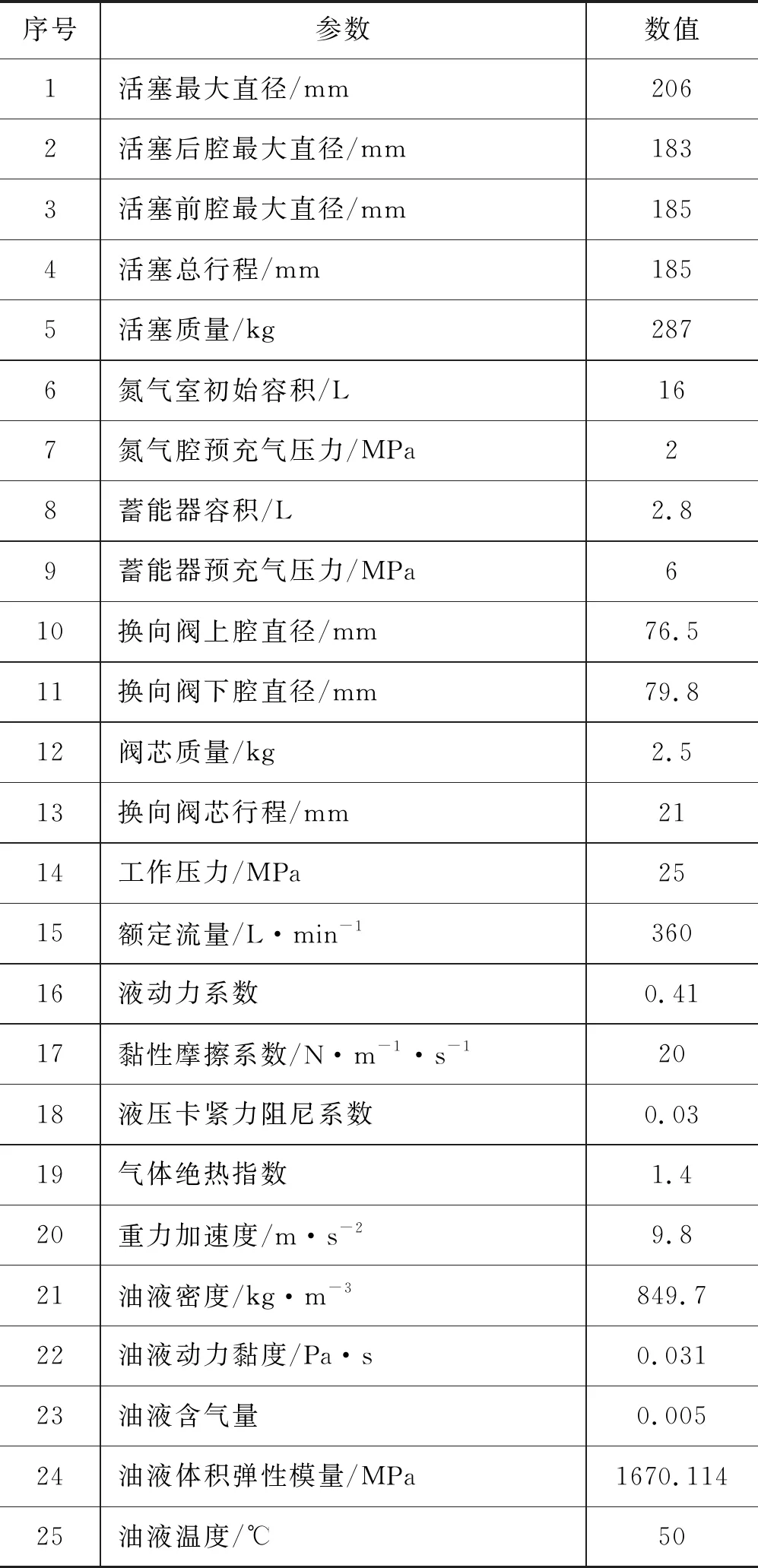
表1 整机仿真模型主要参数

2.2 正交试验设计

正交试验方法是利用正交表科学地安排与分析多因素的研究手段。该方法主要包括试验目标选择、因子-水平表确定、正交试验方案设计以及试验结果统计分析等步骤。

1) 因子-水平表

影响碎石器内部气穴现象的因素有工况参数及结构参数等，其为多因素、多水平的实际条件。经实践经验和仿真结果共同表明，影响气穴的代表性参数有：工作压力A、蓄能器压力B、蓄能器初始容积C、活塞前腔杆径D。同时，假定A的水平取值分别为：23，25，27，29 MPa；B的水平取值分别为：5.0，6.5，8.0，9.5 MPa；C的水平取值分别为：2，3，4，5 L；D的水平取值分别为：185，187，189，191 mm。这样，将所考察的因子和水平列成如表2所示的形式。

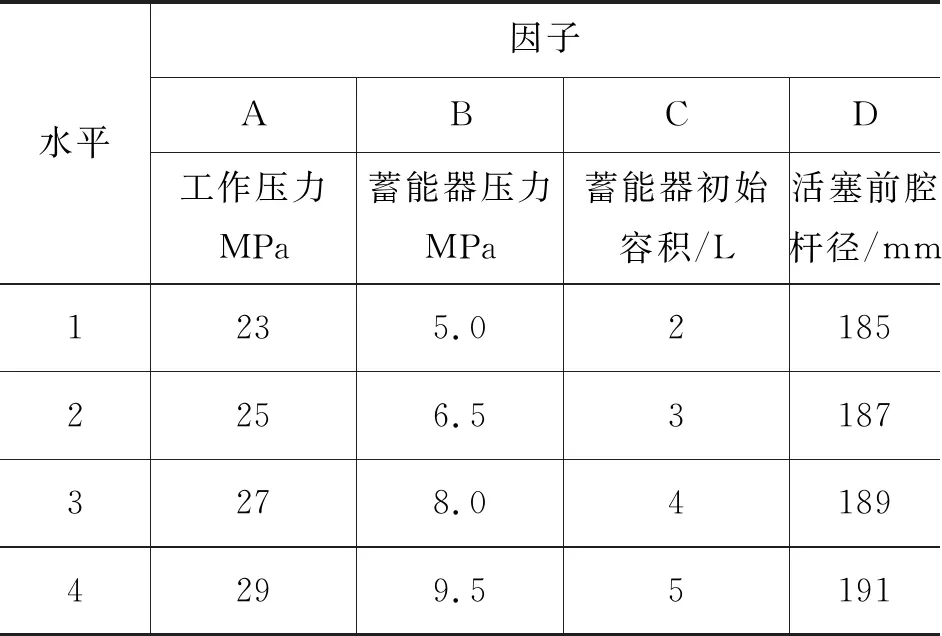
表2 正交试验因子水平表

2) 正交试验方案

由表2可知，需要设计一个4因子、4水平的等水平正交表L16(44)。这样，可得16个具体的试验条件，对应的试验方案见表3。

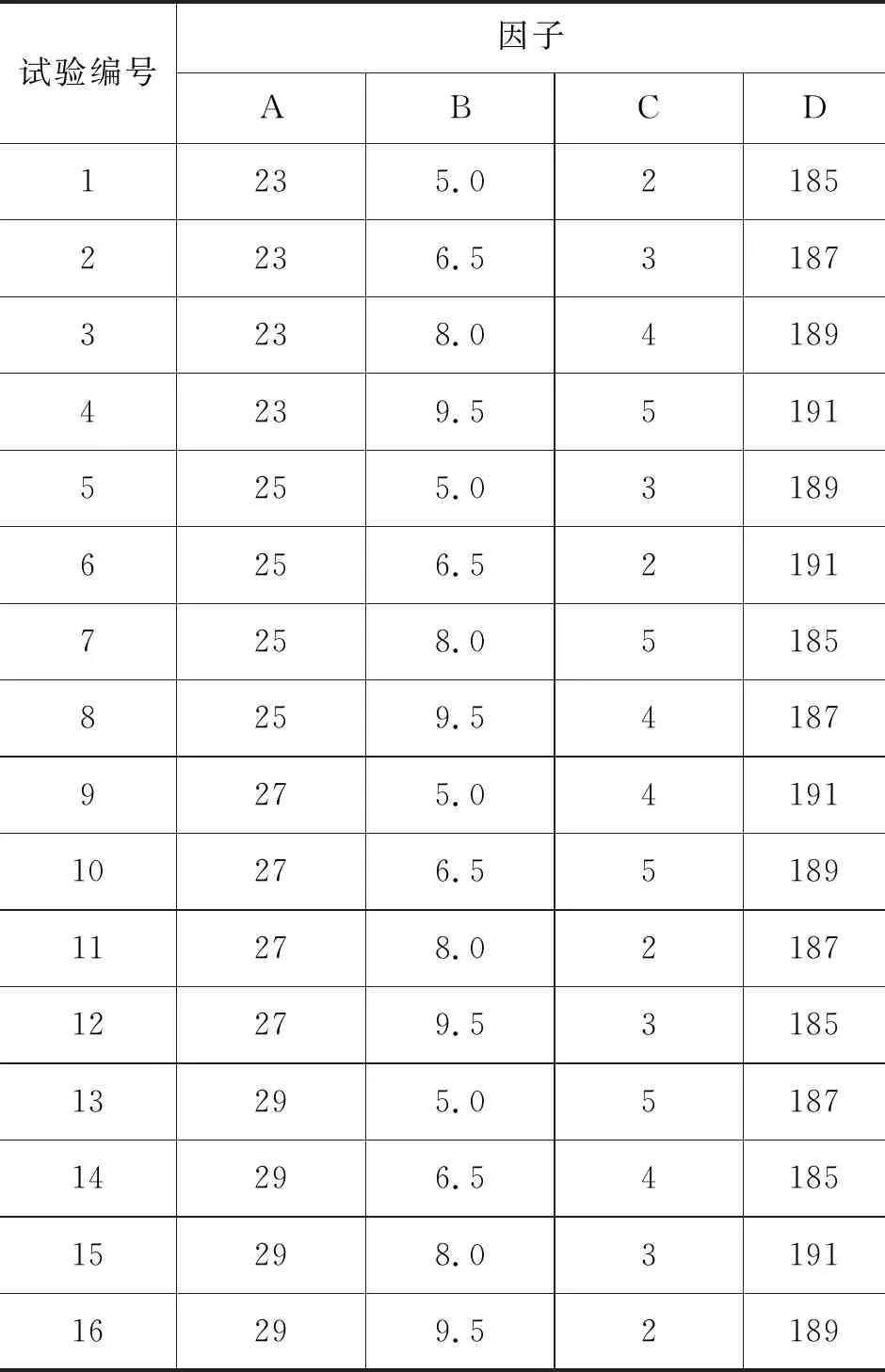
表3 L16(44)正交试验方案

3) 正交试验目标

由文献[14]可知，碎石器冲程打击钎杆瞬间由于补液不足造成活塞后腔的压力降至最低。因此，本研究以提高活塞后腔的最低压力为试验目标。

3 AMESim仿真结果与分析

根据本研究目标同时结合前文正交试验方案，在AMESim平台中设定对应变量取值，同时设置仿真时间(10 s)与步长(0.0001 s)，最后运行仿真。待计算完成后获取4～4.5 s之间不同试验对应活塞后腔瞬时压力，见图2。

图2 不同试验条件下活塞后腔瞬时压力曲线对比

由图2可知，不同试验对应瞬时压力曲线呈连续周期性变化，变化周期非常接近，大约为0.27 s。不同压力曲线对应最低压力都比较小，有些甚至接近0。经对比，活塞后腔出现最低压力的瞬间恰好对应于活塞运动至下死点，即活塞头部与钎杆尾部撞击的位置。这与工程实际中碎石器内部出现气蚀的物理真相非常接近，具体见图3。

图3 工程实际中碎石器内部出现的气蚀真相

由图3可知，碎石器实际工作中缸体内壁由于长期承受气穴影响，表面金属开始受到侵蚀和剥落，不断出现海绵状小洞穴，严重之处甚至呈现凹坑，即出现了气蚀问题。经确认，此位置正好对应活塞与钎杆的撞击过程。这一真相与仿真中活塞后腔出现最低压力的位置完全吻合，进一步验证了仿真方法的适用性及仿真结果的准确性。

为进一步分析因子对活塞后腔最低压力的影响程度，同时根据平均压力高低确定最优水平组合，紧接着获取不同试验对应最低压力正交试验分析表，见表4。

由极差法可知，表4中影响最低压力的各因子主次关系为：D>C>B>A，即活塞前腔杆径是主要因子，其余3个因子对最低压力的影响程度相当。随着活塞前腔杆径地增大，最低压力不断减小。究其原因是增大杆径后削弱了回程作用力，缩小了活塞冲程位移，减小了冲程速度，增大了活塞与阀芯速度的不匹配程度。最低压力与蓄能器初始容积负相关、与蓄能器压力正相关，与工作压力没有表现出明显的相关性。

进一步地，根据正交试验目标，表4反映出最优水平组合为A3B4C1D1，即工作压力为27 MPa，蓄能器压力为9.5 MPa，蓄能器初始容积为2 L，活塞前腔杆径为185 mm。接着获取最优水平组合对应活塞后腔瞬时压力曲线，见图4。

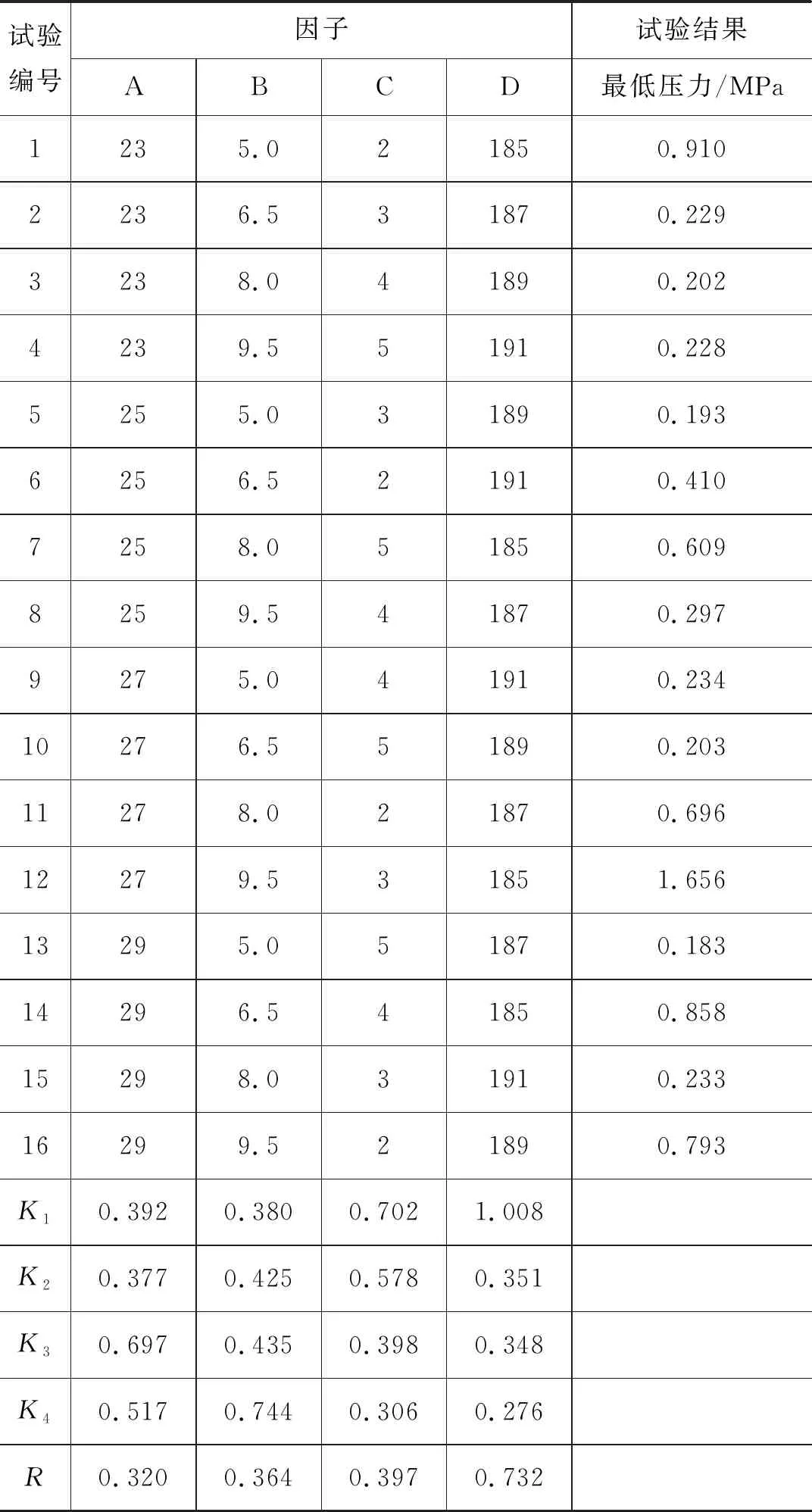
表4 活塞后腔最低压力正交试验分析表

由图4可知，最优水平组合对应最低压力为2.29 MPa。经查，油温为50 ℃时对应的空气分离压(绝对压力)为0.042 MPa，优化后的最低压力远高于相应空气分离压。

图4 最优水平组合对应活塞后腔瞬时压力曲线

然则，AMESim模型为一种集中参数模型，该模型假定系统中各变量是均布的，无法反映流体质点的运动空间，不能获取不同空间位置处的流体属性变化。因此，需要采用CFD仿真模型来计算流体质点随空间位置的运动规律。

4 CFD仿真模型建立与结果分析

4.1 CFD仿真模型建立

CFD问题的求解过程已经规范化，鉴于软硬件条件的多样性、CFD仿真程序的复杂性以及求解过程的稳定性等，CFD比较适应于商用软件，人为的操作过程主要有以下几个方面：

1) 三维内流道有限元模型建立

气液联合式碎石器工作动力源自于高压油液及带压氮气，其中氮气腔和蓄能器中与氮气相关的参数变化规律是明确的。因此，在建立三维内流道有限元模型时只考虑碎石器中的油液流道结构。

根据静压支撑特性理论[16]，考虑内部所有摩擦副之间的内泄漏，其中活塞与缸体、阀芯与阀套配合间隙中的油膜厚度分别为0.12 mm及0.08 mm。以冲程起始位置作为初始内流道进行网格划分，具体的三维内流道有限元模型见图5。该图中，在封闭表面内生成笛卡尔网格，动态区域则生成计算稳定，节点最多的结构化网格。

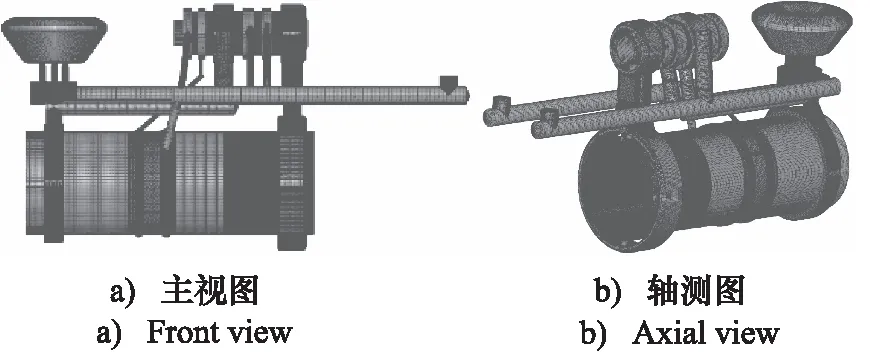
图5 考虑内泄漏的三维内流道有限元模型

2) 仿真参数的设定

(1) 边界条件 CFD问题的边界条件指计算域边界上给定的求解变量或其一阶导数随空间坐标及时间的变化规律。气液联合式碎石器作为液压挖掘机的执行元件，主运动件活塞的动力源自于内部高压油液及带压氮气，阀芯的动力源自压力差及自重，高压蓄能器则根据系统内工作压力的变化进行充液或者排液。

因此，选取压力作为进出口边界条件，选择流量作为蓄能器隔膜进口边界。另外，三维内流道中活塞和阀芯对应壁面都为周期性的运动壁面，需要利用相应的动网格技术来模拟其动作过程。

所有边界条件的数值均按照AMESim仿真结果进行设定，获取4～4.5 s内活塞与阀芯速度、进口与出口压力、蓄能器进口流量随时间的变化规律分别见图6～图8。

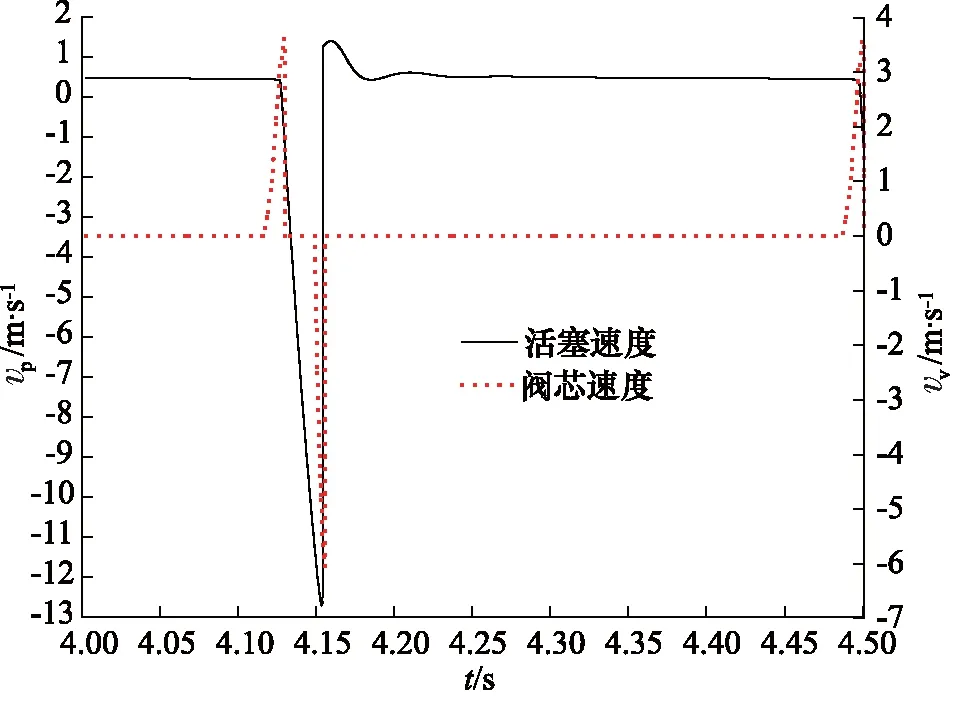
图6 活塞和阀芯速度随时间变化规律

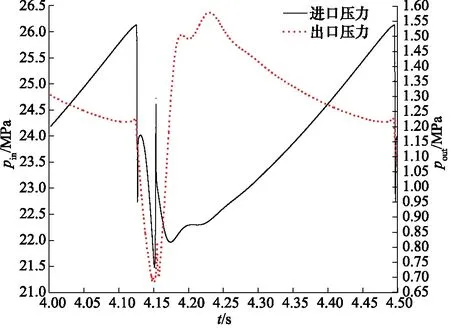
图7 进口和出口压力随时间变化规律

图8 高压蓄能器进口流量随时间变化规律

(2) 流动介质 根据碎石器用液压油的黏度范围以及工作条件，选取46#矿物油作为流动介质。按照该矿物油的含气状态，设定自由气体含量为0.5%以及油温为常用值50 ℃。列出该工况条件下油液的物理属性，见表5。

表5 46#矿物油介质属性

(3) 时间步数 在不失计算准确性及加快计算速度的前提下，采用变时间步长进行数值模拟；在确保每个时间步内计算收敛的前提下，设置其中最大迭代次数为150，设定计算周期数为2。

(4) 湍流模型及气穴模型 在碎石器工作过程中，运动速度急剧变化的活塞和阀芯带动内部流体质点的速度及方向不断发生剧烈变化。经计算容腔中油液的雷诺数为9863，内部流动属于湍流状态。因此采用非直接数值仿真中Reynolds平均法求解时均化的Navier-Strokes方程，确定RNGκ-ε涡黏模型来模拟内部湍流。

根据含气油液的相间作用，选择平衡溶解气体模型。该模型利用气体运移原理来确定溶解于流体中非冷凝气体的质量分数，并假设溶解气体处于平衡状态。

4.2 计算结果与分析

1) 网格及收敛标准无关性验证

网格作为内流道模型的表现形式，同样也是数值计算及结果分析的基础，对于求解过程的稳定性及计算结果的准确性有着非常重要的影响。收敛标准控制着每个时间步内迭代计算精度，进一步影响整个流场计算结果的准确性。因此，为了尽可能消除人为因素对模拟结果的影响，需进行无关性验证。

(1) 网格无关性验证 由图5可知，网格模型中无任何细碎面，网格质量良好。因此，只需验证网格节点数对计算结果的影响。本研究对比5组网格节点数，不同条件的判断标准为出口平均流量，具体计算结果见表6。

表6 不同节点数对应的计算结果

由表6可知，节点数增大至235.985万时，针对网格数大于600万，节点数高于500的计算结果，计算得到的偏差率降低至1%以内。因此，为了加快求解速度，选择节点数为235.985万的网格模型。

(2) 收敛标准无关性验证 验证收敛标准降低到一定值后计算结果基本不发生变化。本研究分别设置4组收敛标准，即0.1，0.06，0.02，0.01，0.001，不同条件的判断标准为出口平均流量，具体计算结果见表7。

表7中，每个时间步内的收敛标准对计算结果的影响非常小。然而，为了进一步提高计算结果的准确性，收敛标准定义为0.01。

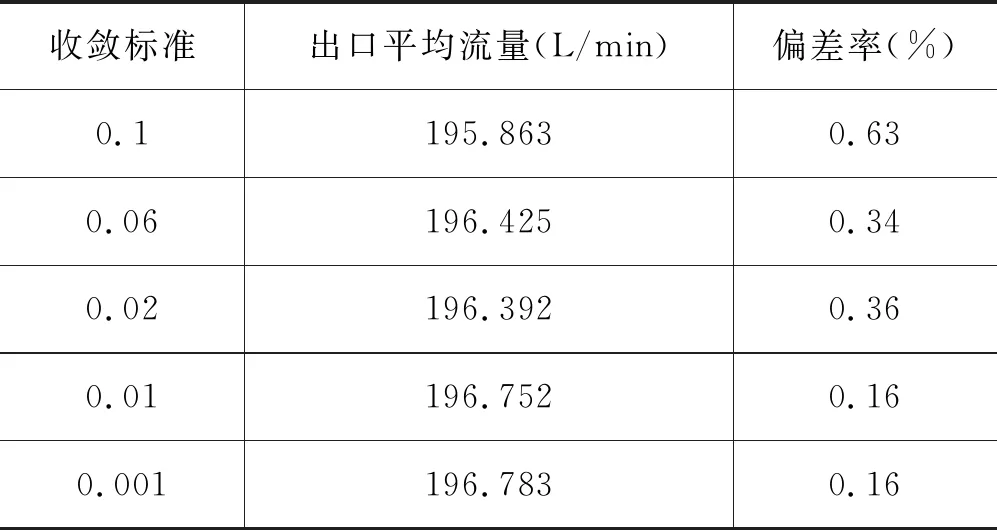
表7 不同收敛标准对应的仿真结果

2) 气穴流场分析

气液联合式液压碎石器工作时，内部流场时刻处于变动过程。因此，根据研究重点的不同，本研究选取冲程打击过程中不同时刻对应活塞后腔径向横截面上总气体体积分布云图，见图9。

由图9可知，从活塞冲程到无限接近钎杆的时刻0.3964 s开始，一直到撞击钎杆瞬间0.3969 s结束，在这段时间内不同时刻对应径向横截面上总气体体积分数接近于零，即此阶段活塞后腔气穴现象相当不明显或者未出现气穴现象。为进一步验证打击过程活塞后腔是否出现了气穴，在数值计算进程中对打击点的瞬时压力进行检测，获取打击点压力-活塞位移对应曲线，见图10。

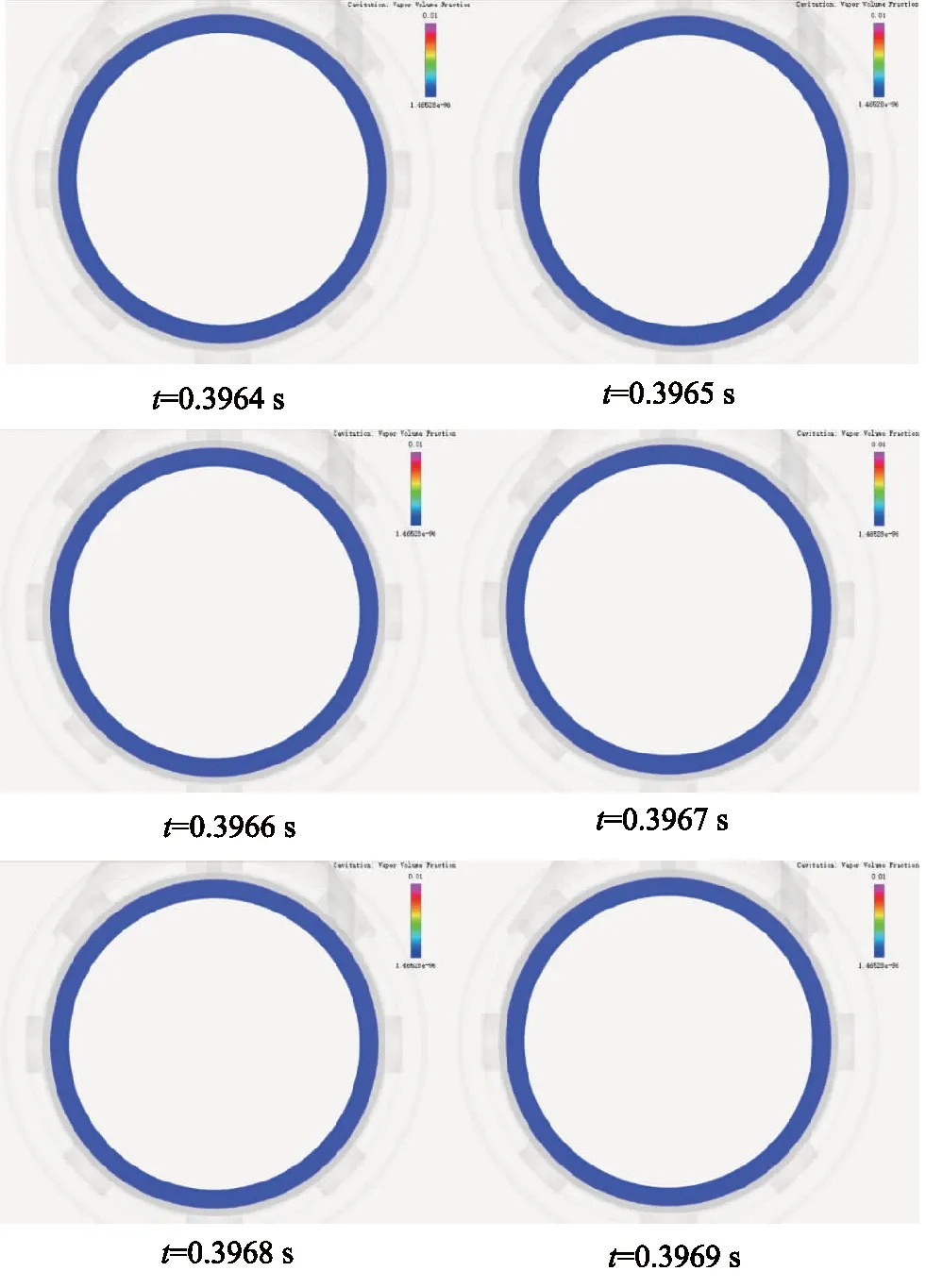
图9 活塞打击过程后腔径向横截面上总气体体积分布云图

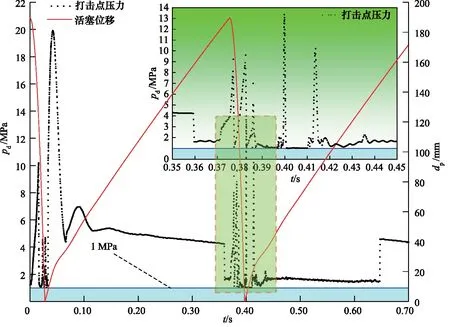
图10 打击点压力-活塞位移对应曲线

由图10可知，在活塞打击钎杆的过程中，打击点压力出现了幅值较大的波动。然而该过程中任意时刻对应瞬时压力都大于1 MPa，远高于油液在50 ℃时对应空气分离压0.042 MPa。因此，采用最优水平组合时溶解于油液中的气体不会出现分离，进一步说明了活塞后腔不会出现气穴，进而解决了碎石器内部的气蚀问题。

5 结论

(1) 不同试验对应活塞后腔最低压力都很小，且出现最低压力的时刻对应活塞运动至下死点，即活塞头部和钎杆尾部撞击的位置，这与实际工程中出现气蚀的零件以及其对应气蚀位置完全吻合；

(2) 活塞前腔杆径是影响活塞后腔最低压力的主要因子，蓄能器初始容积与压力、工作压力对其影响程度相当。为增加最低压力，应尽可能减小活塞前腔杆径及蓄能器初始容积，同时增大蓄能器压力；

(3) 活塞后腔最低压力最优的水平组合为工作压力27 MPa、蓄能器压力9.5 MPa、蓄能器初始容积为2 L、活塞前腔杆径185 mm，经验证该组合对应最低压力为2.29 MPa；

(4) CFD计算结果进一步印证了采用最优水平组合时溶解于油液中的气体不会出现分离，即在任意时刻活塞后腔都不会出现气穴，继而解决了碎石器内部出现的气蚀问题。