基于CFD的齿轮泵实际最优端面间隙确定方法

魏列江， 刘榕民， 强 彦， 姜宏暄， 胡 铮

(1.兰州理工大学 能源与动力工程学院， 甘肃 兰州 730050； 2.北方车辆研究所， 北京 100071)

引言

齿轮泵广泛应用在各种液压机械上，主要优点是：结构简单紧凑，体积小，重量轻，自吸性能好，工作可靠，寿命长等[1]。齿轮泵的端面间隙大小是其内泄漏和黏性摩擦损失最重要的影响因素，工程实践中确定合适的端面间隙对于提高齿轮泵的效率、延长其使用寿命意义重大。郑跃鹏[2]对液压齿轮泵两种主要的端面间隙补偿结构分别进行了详细介绍，并分析说明了两种结构的工作原理以及优缺点。甘学辉等[3]通过对齿轮泵端面间隙油液流动进行详细研究，提出了常用工况时，齿轮泵端面泄漏造成的容积效率损失与端面黏性摩擦造成的机械效率损失之和最小条件下的最优端面间隙解析表达式。陈英等[4]从节能的角度出发建立齿轮泵间隙优化模型，得到各型号泵的优化间隙，并求得优化间隙下的效率，与试验结果进行了对比分析。钱林峰[5]以泄漏功率损失和黏性摩擦损失之和总功率损失最小为设计目标，将轴向间隙作为设计变量，将不确定性理论引入到设计过程中，利用优化设计原理计算出齿轮泵最优轴向间隙。王强[6]对纯水齿轮泵中齿轮转子与侧板的最佳轴向间隙设计进行了理论研究。廖传林[7]研究探讨使用二级脱盐水时外啮合齿轮泵齿轮端面间隙的确定方法。浮动侧板的正面和背面在高压油的作用下，轴向空间位置不断发生变化，进而会改变端面间隙大小。李玉龙[8]等对浮动轴套进行受力分析，构建出浮动轴套的动力学模型，并利用龙格库塔法在一个啮合周期内的迭代计算，获得端面间隙的动态仿真结果。DHAR S等[9]提出了一种新的建模方法，用于研究外啮合齿轮机滑动侧衬套和正齿轮之间的横向润滑间隙，还计算了一系列操作条件下的间隙高度和由此产生的润滑间隙功率损失。BATTARRA M等[10]提出了一种确定外啮合齿轮泵齿间压力变化引起的可变激励载荷的系统方法。考虑到啮合过程中出现的现象，根据齿轮的角度位置估算压力和扭矩。THIAGARAJAN D等[11]提出了一种新的非对称平衡外啮合齿轮泵横向润滑界面流固耦合模型。通过考虑与之相关的特定设计变量，确定横向衬套上的最佳平衡面积，从而实现最佳轴向平衡。TORRENT M[12]等根据定义浮动衬套润滑的方程，建立了浮动衬套运动的键合图模型。CFD软件对于齿轮泵内部的流场分析有可视化的特点，可以用来分析实际工况下齿轮泵的流场变化情况。刘巍等[13]以某型号高压大排量齿轮泵为模型，运用CFD 软件解析齿轮泵内部流场并根据侧板结构特点建立压紧力和反推力的求解微分方程，通过积分方法求得旋转一个轮齿啮合周期内的侧板倾覆力矩变化规律，同时通过建立齿轮泵工作腔压力测试系统对该理论分析结果进行验证。杨永敏等[14]利用专业泵阀CFD仿真软件对齿轮泵10个齿槽平均压力分布和浮动侧板表面压力分布等进行了分析，并根据分析结果建立了引入修正系数的浮动侧板表面压力及其力矩的计算公式。黄健等[15]利用动网格技术，对润滑系统中的供油齿轮泵端面间隙和容积效率之间的关系进行了分析。张静等[16]采用Fluent动网格技术，对斜齿轮泵在工作过程中内部瞬态压力场和速度场的分布情况进行详细分析。文昌明等[17]通过用PumpLinx软件对齿轮泵实例进行详细描述，为齿轮泵的仿真过程提供参考案例。李洪涛[18]对CB-E50型齿轮泵中密封圈压缩量和衬套的静力平衡进行分析和计算，对原有密封圈进行了修正设计。王安麟等[19]针对外啮合齿轮泵浮动侧板在多工况下进行试验，得出浮动侧板的正面压力分布为非对称分布，得出浮动侧板正面所受浮动力矩会随着工况的变化而变化。

上述对端面油膜反推力的研究偏于理论推导，端面间隙与反推力的关系表达式复杂，不利于工程实际中齿轮泵最优端面间隙的实际确定。实际中，最优端面间隙是该间隙下端面油膜反推力与侧板背面引入的高压油压紧力达到平衡时才可实际获得，故需要同时确定最优间隙下所对应的油膜反推力与浮动侧板背面所需高压油压紧力。本研究采用CFD软件(PumpLinx)获得常用工况下给定端面间隙与端面油膜平均反推力仿真分析数据，利用最小二乘法拟合得到小间隙变化时的端面油膜平均反推力线性化方程，将文献[5]计算得到的最优端面间隙值代入该方程，反解出浮动侧板背面所需高压油压紧力，进而通过调整浮动侧板背面密封圈围成的高压区形状，使齿轮泵的实际端面间隙在常用工况下处于最优值。

1 研究对象

本研究对象为某型号外啮合齿轮泵，额定压力2.5 MPa，额定转速3000 r/min，其主要几何结构参数和结构示意图如表1和图1所示。假定齿轮泵装配后，左右浮动侧板和齿轮侧面形成的端面间隙大小相同且呈左右对称分布，又因两浮动侧板结构相同，则两浮动侧板在轴向受到液压力的情况相同，以齿轮泵的右浮动侧板作为研究重点。

表1 主要几何结构参数

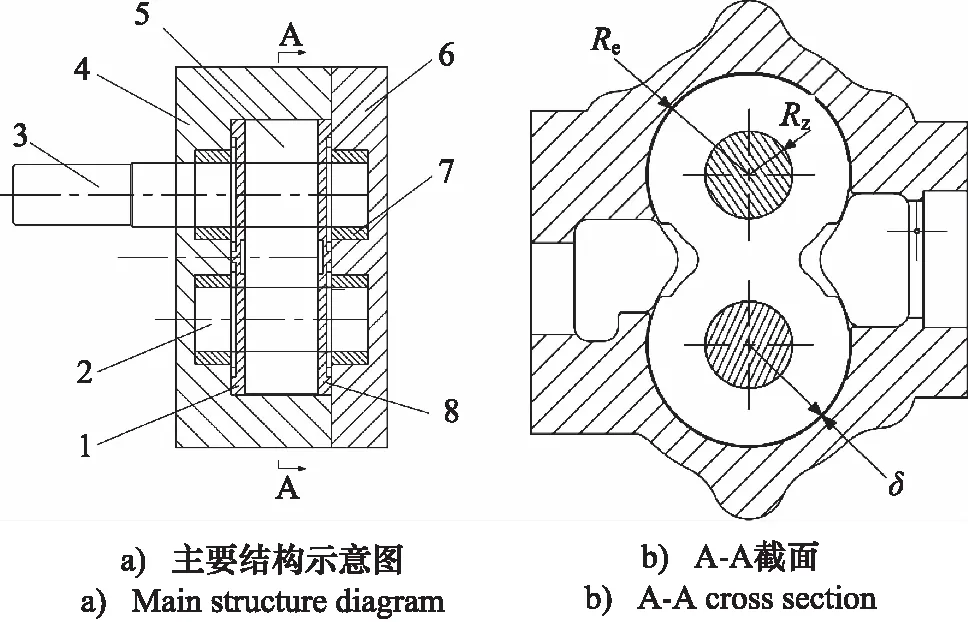
1.左浮动侧板 2.从动轴 3.主动轴 4.壳体 5.齿轮副 6.端盖 7.轴承 8.右浮动侧板

2 建立仿真模型

2.1 网格参数设置

在Croe中建立齿轮泵三维模型，通过布尔运算获得齿轮泵的流体域后，以stl格式导入PumpLinx软件。首先对流体域的各组成部分进行区域划分并命名，然后生成进出油口、高低压卸荷槽、齿轮转子区等部分的网格，如图2所示。

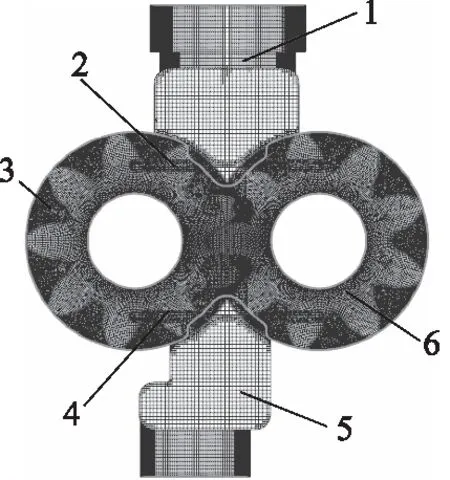
1.进油口 2.进口卸荷槽 3.齿轮转子区 4.出口卸荷槽 5.出油口区 6.端面间隙

在齿轮转子区域的高级动网格模板中生成高质量结构化网格：设置端面间隙网格层数为5，网格尺寸为Fine，并设置内外径等结构参数。将除齿轮转子区的静网格模型设置为六面体为主的笛卡尔网格：临界边角30°，最大网格尺寸0.008，最小网格尺寸0.0002，面网格尺寸0.005。接着利用MGI命令设置动网格模型和静网格模型间的交互面，如图3所示，并设置每转过一个轮齿步长为40，仿真转数为5转，总步长为1800步，可以较好的保证仿真软件输出结果的稳定性。

图3 仿真模型交互面

2.2 计算边界条件和油液介质参数

为得到常用工况下给定端面间隙下的端面油膜反推力，设置端面间隙为0.03，0.04，0.05，0.06，0.07 mm。仿真计算中，选择内部流场的计算模型为标准κ-ε湍流模型和Constant Gas Mass Fraction全空化模型。全空化模型是基于两相流模型的思想，用Rayleigh-plesset方程求解气泡变化的动态过程，综合考虑了液体的可压缩性以及油液的蒸发和凝结过程[20]，其中固定气体质量分数表征油液含气量的多少。在仿真模型中设置常用工况如表2所示，油液介质的具体参数见表3。

表2 常用工况

表3 油液介质参数

2.3 网格无关性验证

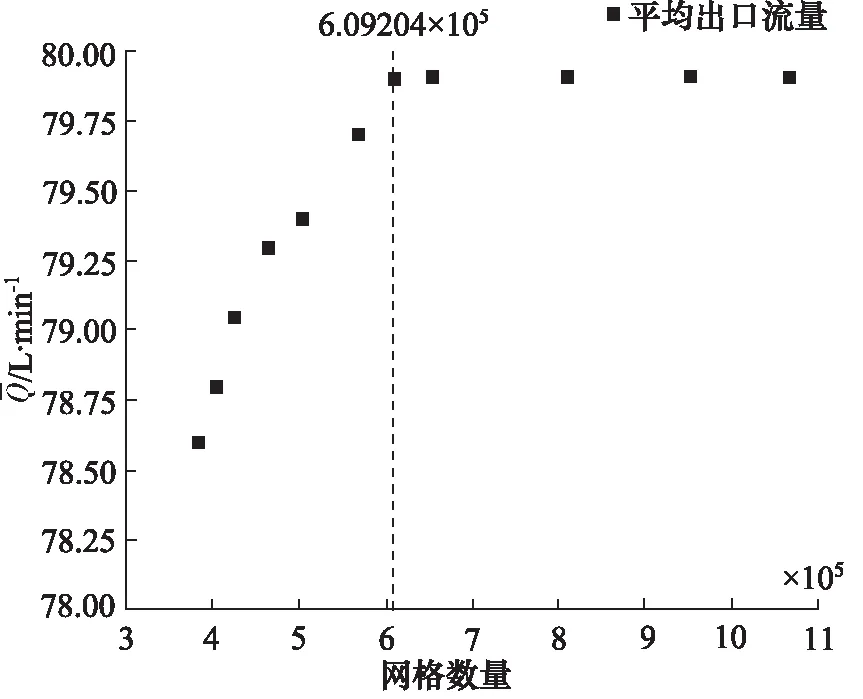
图4 齿轮泵网格无关性验证

3 最优端面间隙

齿轮泵的端面间隙形成于齿轮副端面和浮动侧板之间的配合面，液压油填充端面间隙形成端面油膜。端面间隙处的油液流动为压差剪切流动，由端面间隙引起的总功率损失P为油液泄漏功率损失Pq与油液黏性摩擦引起的功率损失Pf之和，即：

P=Pq+Pf=Δpq+Pf

(1)

式中，q—— 端面间隙泄漏量，m3/s

Δp—— 齿轮泵进出口压差，Pa

以总功率损失P最小作为设计目标，以齿轮泵端面间隙s为设计变量。令∂P/∂s=0，得到齿轮泵最优端面间隙值s*为[3]：

(2)

式中，Rf—— 齿根圆半径

Rz—— 齿轮轴半径

μ—— 油液动力黏度

ω—— 旋转角速度

其中，Kf和Kq旋转分别为：

(3)

式中，Re—— 齿顶圆半径

R—— 节圆半径

(4)

式中，βH—— 高压区包角，取60°

2βB—— 过渡区包角，取20°(见图7)

将表1～表3各相关参数代入式(2)中，得到在表2工况下齿轮泵的最优端面间隙值为0.05 mm。

4 浮动侧板轴向力平衡

在分析过程中假定高压油压紧力和端面油膜反推力的作用线完全重合。则当高压油压紧力和端面油膜反推力相等时，浮动侧板达到力平衡状态。浮动侧板所受作用力由三部分组成，分别是齿轮副和浮动侧板间端面油膜反推力F1、高压油压紧力F2和密封圈弹性力F3，如图5所示。其中，经计算在浮动侧板轴向力平衡中端面间隙为0.05 mm时密封圈弹性力为8 N，在轴向力分析中占比很小，因此将其作忽略处理。

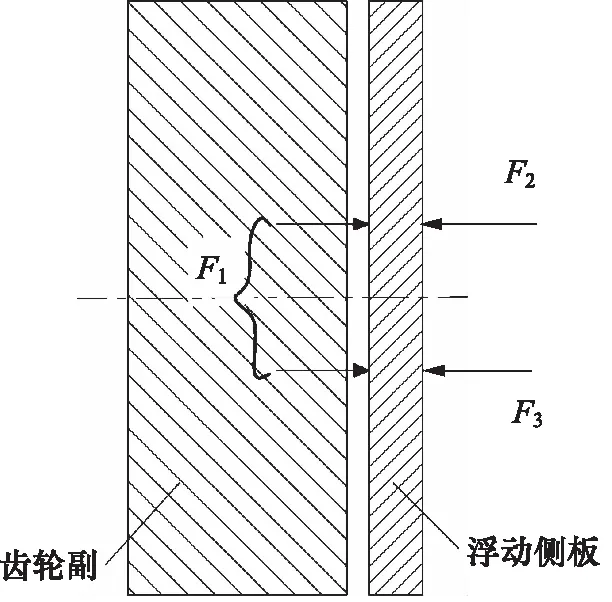
图5 浮动侧板受力示意图

4.1 高压油压紧力

在装有密封圈的浮动侧板背面，低压区Sd的油液压力为进口压力，则低压区的油液压紧力为0 N。在Croe软件中测量出侧板背面密封圈围成的高压区面积Sg为1495 mm2(如图6所示)，假设由出油口引到浮动侧板背面的高压油均匀分布在高压区Sg，齿轮泵出口压力为2 MPa，则浮动侧板背面的高压油压紧力F2=1495×2=2990 N。

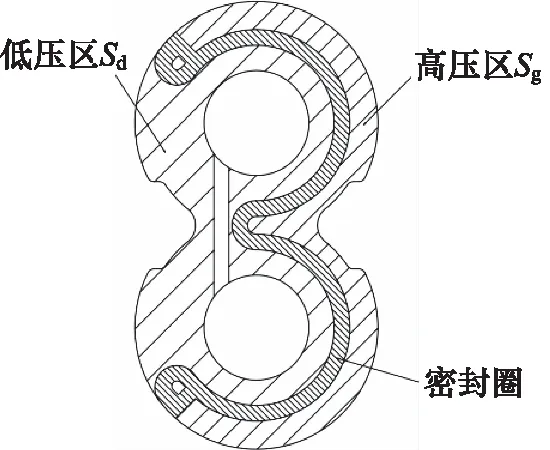
图6 浮动侧板背面区域划分

4.2 端面油膜反推力

齿轮泵的运转过程中，油液经齿轮副端面和浮动侧板之间的配合面流入端面间隙，形成油膜静压支撑，产生端面油膜反推力。其中，端面间隙在轴向的有效面积大小是齿轮副端面的表面积。在表2工况下，所得到5组给定端面间隙下的端面油膜反推力压力分布云图基本相同，以端面间隙为0.05 mm为例进行仿真分析，得到一个旋转周期内(主动齿轮转角从φ=0°变化到φ=360°)，端面油膜反推力随齿轮转角变化的压力云图，如图7所示。

由图7可看出，在一个旋转周期内，端面油膜反推力的压力分布并非呈左右对称分布。分布区域随齿轮转角的变化而变化，各齿轮转角下端面油膜反推力压力分布所占区域大致相同。设置端面间隙为0.03, 0.04, 0.05, 0.06, 0.07 mm的仿真模型，对所得数据进行后处理，得到各给定端面间隙下端面油膜反推力随时间的变化规律，如图8所示。

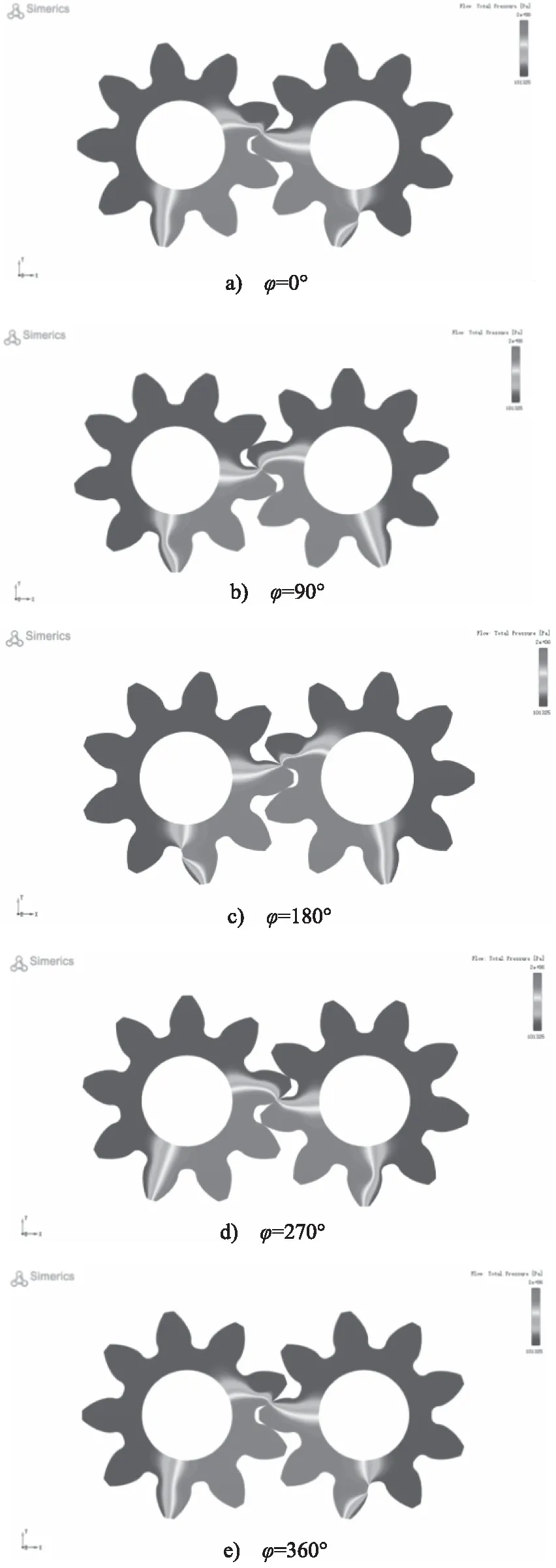
图7 端面油膜反推力压力云图

由图8可看出，当给定端面间隙从0.03～0.07 mm 变化的过程中，端面油膜反推力随时间的波动幅度明显变小，并且随着端面间隙的增大，端面油膜反推力反而变小；反之，随着端面间隙的减小，端面油膜反推力将变大。在一个旋转周期内，对图8各端面间隙下总反推力求平均值，并用最小二乘法进行线性化拟合，得到间隙小范围变化时的端面油膜平均反推力曲线方程，如图9所示。

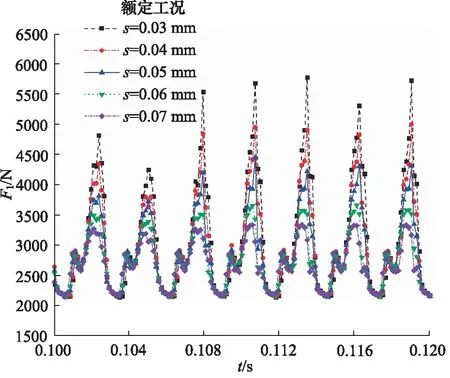
图8 端面油膜反推力

由图9得端面油膜平均反推力方程为：

(5)

式中，s—— 给定端面间隙值，mm

从图9可看出，当端面间隙从0.03～0.07 mm变化的过程中，端面油膜平均反推力从3106 N减小到2698.5 N，即端面间隙越大对应的端面油膜反推力越小。将最优端面间隙值0.05 mm代入端面油膜平均反推力方程，得到平均反推力为2900 N，而现有高压油压紧力为2990 N。因此，为确保在常用工况下齿轮泵的实际端面间隙处于最优值，通过在浮动侧板的上下侧切除相同面积，如图10所示，将浮动侧板背面高压区面积调整为1450 mm2。

图9 端面油膜反推力线性化拟合

图10 浮动侧板高压区面积调整

4 结论

(1) 通过CFD软件对常用工况下不同端面间隙进行仿真分析， 得到5组不同端面间隙对应的端面油膜平均反推力，经曲线拟合后得到间隙小范围变化时的端面间隙与端面油膜平均反推力的线性方程；

(2) 通过对齿轮泵的浮动侧板进行轴向的力平衡分析，得到常用工况下与高压油压紧力相等的端面油膜平均反推力，代入上述方程后可以获得该工况下齿轮泵的实际端面间隙值；

(3) 为使常用工况下实际端面间隙值等于最优端面间隙值，应通过调整浮动侧板背面密封圈围成的高压区面积，让其等于最优端面间隙值对应的浮动侧板背面高压区面积。