互信息深度稀疏自编码融合DLSTM预测网络

李江坤，黄海燕

华东理工大学 化工过程先进控制和优化技术教育部重点实验室，上海 200030

在现代流程化工业生产过程中，对于生产安全、能源节约、改善产品质量有着严格要求。这些指标很大程度上依赖长时间有效监控和对质量的生产调控。对于难以直接在线测量的关键变量通常采用软测量的方法对数据进行在线处理预测[1-3]。软测量成功应用于冶金工程、化工过程、生物工程和制药工程等一些大型流程工业生产活动。

软测量技术可以划分为主成分模型（白盒模型）和数据驱动模型（黑盒模型）。数据驱动建模以多变量统计和机器学习方法为主，如主成分回归（PCR）[4-5]、偏最小二乘回归（PLSR）[6-7]、支持向量回归（SVR）[8]和人工神经网络（ANN）[9-10]。由于这些方法大多是浅层网络结构，因而在一定程度上限制了非线性映射能力。

相比于传统的神经网络方法，深度神经网络DNN对于数据特征提取更加具有优势，在一定程度能够捕捉到数据重要特征，也增强对非线性数据处理能力，例如文献[11]采用深度置信网络DBN对工业原油蒸馏装置的95%重柴油临界点进行估计。文献[12]提出一种半监督层叠式极限机学习网络，用来提取标签数据和无标签数据的样本特征信息。然而，大多数基于深度神经网络软测量方法的假设条件是样本独立且同分布，但实际工业过程中变量之间存在动态和相互影响关系。因此，对于流程化工业生产过程动态建模至关重要。例如，线性动态系统[13]、动态偏最小二乘建模[14]。但浅层的动态特征提取方法对复杂且非线性的模型无法有效处理。最近，一些动态网络方法如循环神经网络RNN[15]和长短期记忆网络LSTM已经被应用在工业软测量建模任务中[16]。其中，LSTM网络通过增加三个控制门构建细胞记忆单元，从而解决传统RNN网络梯度爆炸和梯度消失问题。LSTM网络也能够学习序列数据的内部独立性与相关性，因此适用于动态建模。文献[17]采用长短期记忆网络提取间歇过程质量预测的动态信息。文献[15]基于高斯-伯努利约束玻耳兹曼机（GRBM）和递归神经网络（RNN），采用概率序列网络（PSN）融合无监督特征数据的提取和有监督动态建模方法，提高建模精度。文献[18]结合空间相关性提出大气污染物浓度预测的记忆扩展LSTM模型。文献[19]通过引入目标变量，提出带监督的长短期记忆（SLSTM）网络用于工业过程质量预测。借鉴图像处理深度CNN卷积神经网络[20]中卷积、池化、卷积等重复深度操作，以达到对数据深度特征提取。本文对多变量数据通过深度编码解码方法进而提取深度特征。首先将原有稀疏自编码器由原来的单隐层进行扩展至多隐层，并引入互信息因子作为重构损失权重，以此保证提取特征有效性，采用稀疏自编码器目的在于增加对数据特征提取的鲁棒性，然后搭建多个互信息堆叠稀疏自编码器，并将隐层进行迁移得到互信息深度堆叠稀疏自编码特征提取网络。考虑数据动态性和LSTM网络对序列数据的数据处理优势，本文改进原有LSTM网络的架构，融合Bi-LSTM网络对数据动态特征的处理能力，提出一种深度DLSTM序列数据预测模型。

1 互信息深度堆叠稀疏自编码器

1.1 堆叠稀疏自编码器

稀疏自编码器[21-22]通过单隐含层将输入数据进行高维特征映射，单隐层的结构可以减少网络待定参数，加快网络训练速度，但网络较浅的隐含层不能够学习到原始数据中深层隐含特征，本文对稀疏自编码器进行改进，将编码器隐层进行多层扩展，将普通稀疏编码器改进为堆叠稀疏编码器[23]，结构如图1所示。首先输入层接收原始输入数据x∈Rd,其中d表示输入样本的特征维数，将数据进行非线性变换到第一个隐含层h1∈Rs1,s1为第一隐含层的神经元数目，隐含层的输出为h1：

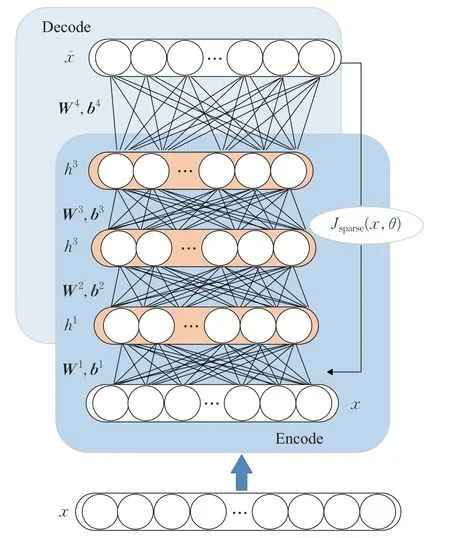
图1 堆叠稀疏自编码器Fig.1 Stacked sparse auto-encoder

其中，W1代表输入层与第一个隐含层连接权重矩阵，b1为第一个隐含层的偏置向量，f(·)表示激活函数，第二个隐含层记为h2,该层的输出记为h2=f(W2h1+b2)，以此类推，可进行多个隐含层的搭建连接，最后的隐含层记为hn,输出为hn=f(Wnhn-1+bn)，网络最后连接的是重构输出层x͂,其输出为x͂=Wohn+bo,Wo代表最后一个隐含层与输出重构层连接权重矩阵，bo为网络最后一层偏置向量。

堆叠稀疏编码网络计算公式如下：

x代表网络输入数据，x͂代表网络输出数据，HW,b(·)为整个稀疏自编码器映射函数，稀疏自编码器的网络结构参数训练主要通过最小化损失函数进行优化，损失函数公式如下：

整个网络参数通过L-BFGS算法进行得出，目的将损失函数达到最小值，其中公式（3）第一项代表误差平方和，其作用是将整个稀疏自编码器的重构误差和达到最小，损失函数的第二项是正则项，也称作权重系数衰减项，该项的作用是避免过拟合现象发生，正则项的系数记为λ1，损失函数的最后一项代表隐含层的稀疏惩罚项，β是该项的系数。L是整个稀疏自编码器的中间隐层和输出层层数总和，Wl代表第l层的每个神经元与第l+1层连接神经元的权重矩阵，s是隐含层的神经元个数，其中KL(ρ||ρ͂j)散度衡量两个分布的差异，计算公式如下：

ρ是稀疏参数，通常设置很小接近于0，在稀疏自编码器中ρ͂j代表隐含层其中第j神经元的平均激活程度，计算公式如下：

其中，aj表示隐层第j个神经元的激活函数输出。

1.2 互信息深度堆叠稀疏自编器

互信息[24]是衡量变量之间相关性的指标，具体定义如下：

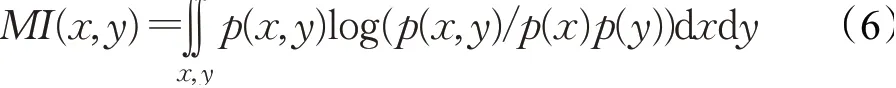
其中，p(x,y)是x,y的联合概率密度，p(x)、p(y)分别代表x、y的边缘概率密度，进一步引入香农熵定义：

得到x、y对应的联合香农熵如下公式：

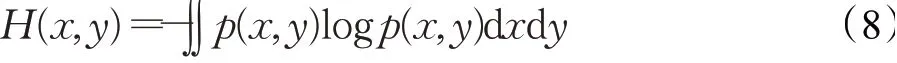
结合以上公式，得到互信息的简化公式：

互信息深度堆叠稀疏自编码器是一种深度网络，其网络组件为互信息堆叠稀疏自编码器，首先搭建单个互信息堆叠稀疏自编码器，设置中间隐含层数为L，每个隐含层神经元数目记为s，输入层与重构输出层的神经元数目相等，都为输入样本的特征维数d，网络损失函数如下：

互信息权重ωn的计算如下：

经过逐层迭代的预训练确定单个堆叠稀疏自编码器的各层权重参数Wl和偏置参数bl，然后将上述过程中搭建好的单个堆叠稀编码器进行迁移，迁移部分是每个稀疏自编码器的隐含层部分，具体迁移结构如图2所示。这里对整个深度堆叠自编码器再进行微调，损失函数定义如下：

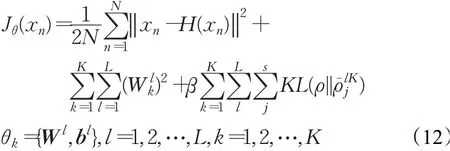
其中，L代表堆叠稀疏自编码器迁移到深度堆叠稀疏自编码器的隐含层数目，K是堆叠稀疏自编码器个数，Hθ(·)表示深度堆叠自编码器映射关系，θ代表所有的网络权重连接矩阵以及偏置参数。在图2中，每一个预训练的堆叠自编码中隐层采用不同颜色标记，深度堆叠自编码器内部的网络则由带有颜色隐层进行迁移堆叠组成，在这一阶段整个网络只需要微调参数就可以达到收敛效果。

图2 互信息深度堆叠稀疏自编码Fig.2 Mutual information deep stack sparse auto-encoder

2 深度DLSTM网络

2.1 LSTM

LSTM网络[25]采用一种复杂的细胞结构，其能够学习并处理长时期序列数据的复杂关系。LSTM细胞机制中存在三个主要的构件，称为输入门，遗忘门和输出门，在整个LSTM网络运行时，三个门能够控制整个信息流的存储和流向，LSTM神经元的结构如图3所示。

图3 LSTM神经元Fig.3 LSTM neuron

从图3中的结构可以看到每一个LSTM细胞结构中在t时刻都包含三个输入信息，分别是上一时刻细胞的状态信息C(t-1)，细胞隐藏状态信息h(t-1)和当前时刻的输入信息x(t)，对于当前t时刻LSTM细胞的计算输出如下，遗忘门f(t)的计算为：

输入门i(t)：

输出门o(t)：

其中，σ是sigmoid激活函数，计算公式如下：

tanh代表双曲正切函数，计算公式如下：

Wfx代表输入数据与遗忘门连接的权重矩阵，Wix是输入数据与输入门连接的权重矩阵，Wox是输入数据与输出门连接的权重，Wcx是输入数据与内部细胞状态门连接的权重矩阵。与之对应，Wfh、Wih、Woh、Wch表示上一时刻LSTM细胞隐藏状态信息h(t-1)与各个门连接的权重矩阵。

关于LSTM记忆细胞内部状态输出C(t)和细胞隐含状态输出h(t)在当前t时刻的计算如下：

2.2 深度长短期记忆网络DLSTM

Bi-LSTM双向长短期记忆网络[26]是基于LSTM网络构成，其内部分别引入前向传输输入序列和逆向传输输入序列，Bi-LSTM具体结构如图4所示。

图4 Bi-LSTM网络结构Fig.4 Bi-LSTM network

同样，反向序列的计算如下：

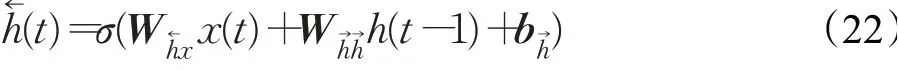
传统LSTM模型能够很好地去处理大多数序列问题。例如在文本任务中，编码层能够将一段话变换成一个固定长度的文本向量，然后再将这个文本向量进行输出解码得到一串输出文字，这种单层LSTM网络结构连接权重可以共享，且结构可以重复，带来较快迭代速度。但由于其网络结构是单层的，对于数据动态特征进行捕捉和记忆由于受到网络单层结构的限制，本文改进普通LSTM长短期记忆网络为深度DLSTM网络结构，通过增加网络的记忆细胞深层次结构以此增强网络对数据动态特征的缓存记忆能力。

结合上述改进方案，并考虑到现实工业系统产生的工况数据为前后有较强相关关系的序列化特征数据，单向数据输入的LSTM网络结构只能建立单一序列预测模型，对于其中的数据动态变化并不能够较好地建立数据特征背后深度预测模型，本文引入双向Bi-LSTM模型使得对于序列化特征数据的处理更加高效，通过对数据进行双向输入来动态融合序列的多维度信息，具体信息融合算法由计算公式（23）～（28）处理。

本文提出深度DLSTM网络，其结构如图5所示。

图5 DLSTM网络结构Fig.5 DLSTM neural network

改进原有LSTM网络提出深度DLSTM长短期记忆网络，采用双层双向LSTM迭代设计结构，该结构中第一层Bi-LSTM中前向输出如下：

反向输出：

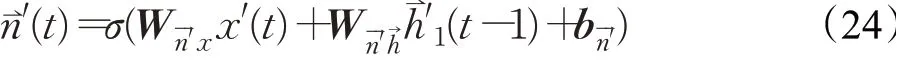
其中，x(t)、x′(t)分别为正向输入序列和反向输入序列，Wn⇀x为输入序列与n⇀连接权重，Wn⇀h为隐含状态与n⇀连接权重，bn⇀为对应的偏置向量。将双向隐层状态n⇀1(t)和n⇀′1(t)合并得到第一层Bi-LSTM输出：

对于第二层Bi-LSTM前向序列输出计算如下：

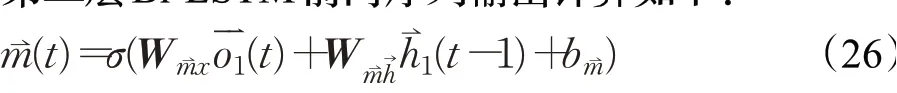
逆向输出计算：

得到第二层Bi-LSTM输出：

每个Bi-LSTM细胞内记忆细胞的隐含状态信号为Bi-LSTM网络的主要信息流，该通道将维持和记忆浅层数据信息。对于第二层也采用Bi-LSTM网络，输入信号为第一层的隐含状态信号o⇀1，第二层Bi-LSTM网络的主要功能是将第一层提取的表层数据信息进行二次深度提取，这样做的目的是将第一层的隐含状态信号o⇀1中包含的高阶动态信息进行筛选。将第二层Bi-LSTM网络得到的o⇀2信息输入到第三层LSTM网络层，得到该层输出为o3(t)，具体计算如下。

控制遗忘门：

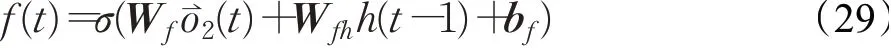
输入门：

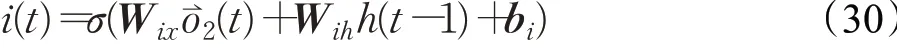
输出门：

细胞内部状态信息：

输出计算如下：

最后将o3进行全连接层映射，得到最终预测结果：

Wyo是全连层接输出权重向量，bo是偏置参数。

3 MI-DSSAE-DLSTM预测模型

MI-DSSAE-DLSTM建模过程分为两个部分，分别是搭建互信息深度堆叠稀疏编码器MI-DSSAE数据特征模型和DLSTM模型。首先是对原始数据进行编码，先进行单个稀疏编码器的构造和训练，得到多个不同的稀疏编码隐含层，每个稀疏编码器预训练根据损失公式（10）通过误差反向传播SGD梯度下降优化网络参数，将得到的单个稀疏编码器的隐含层进行迁移到深度迭代稀疏编码器中，再对整个MI-DSSAE网络进行微调。本文采用互信息深度稀疏自编码器是考虑到在工业现场实际采集的数据具有高噪声、高维度等特点，普通单层自编码器无法有效映射出因变量与自变量之间的非线性关系，采用深度策略一定程度上增加编码器对于非线性数据特征提取的有效性，满足非线性映射需求，而误差函数中的稀疏项可以缓解高噪声数据带来的影响，最后加入互信息权重指标来保证采用深度稀疏自编码提取的数据特征与最后预测的关键质量变量之间相关性。

DLSTM的网络架构包括两个Bi-LSTM层，一个LSTM层和全连接输出预测层，搭建整个MI-DSSAEDLSTM网络流程如图6所示。

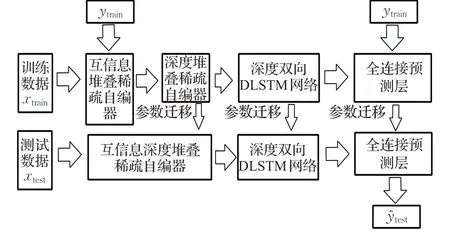
图6 MI-DSSAE-DLSTM建模Fig.6 MI-DSSAE-DLSTM neural network modeling

算法实现过程如图7所示：

（1）将工业传感器采集的数据进行归一化预处理，归一化准则采用z-score，得到预处理后的数据Xn=

（2）设置每个堆叠稀疏编码器的隐层数目L，初始化堆叠稀疏自编码器SAE1、SAE2、SAE3，对每个稀疏自编码器进行参数训练，得到的隐层单元H1、H2、H3。

（3）迁移H1、H2、H3网络层，搭建互信息深度堆叠稀疏自编码器MI-DSSAE，并得到编码后数据是编码后数据特征维数。

（4）设置双层Bi-LSTM网络，LSTM和预测输出全连接网络的结构，初始化各个网络层的参数。

（5）将经过互信息深度堆叠稀疏自编码处理过的新特征输入数据输入到双向Bi-LSTM网络中，双向Bi-LSTM网络的细胞状态C0、h0和根据公式（23）～（34）计算得到输入门、遗忘门、细胞隐含信息、细胞状态信息，输出记为o1(t)。

（6）将o1(t)输入第二层Bi-LSTM网络中，得到该层网络状态输出信号o2(t)。

（7）将单层LSTM的序列输出o3(t)作为全连接层的输入，进行特征加权计算得到最后输出y(t)。

（8）计算网络输出与真实值的差异损失，通过梯度下降SGD算法对整个DLSTM网络参数更新迭代。

4 算法案例

4.1 数据集

脱丁烷塔是石油化工厂重要精炼单元[20]，旨在分裂石脑油和脱硫[21]。该过程主要包括六种装置：顶置冷凝器、热交换器、塔顶回流泵、底部再沸器、回流蓄能器和给水泵液化石油气分离器。其中石脑油流中有丁烷（C4）需要除去，因此需要及时监测丁烷（C4）含量变化。在生产过程中，收集7个相关过程变量用于建模预测丁烷（C4）含量，具体过程变量如图8所示。

图8 模型自变量Fig.8 Independent variables for modeling

模型评价指标选取均方根误差RMSE（root mean squared error）、决定系数R2（R-square）和平均绝对误差MAE（mean absolute error），计算公式如下：

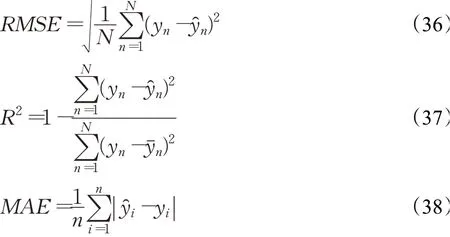
数据集共包含2 394个样本，划分样本为训练集前1 000个，测试集为后1 394个。在进行模型搭建和训练之前，对数据进行归一化处理，以降低模型训练时间，并解决梯度爆炸问题，同时保证量纲统一。对于MI-DSSAE自编码器的编码数据采用z-score方法对数据进行预处理：

x是原始数据，μ、σ是原始数据的均值标准差，z是归一化后的数据。

4.2 模型参数设置

设置互信息堆叠稀疏自编码器隐含层数分别为[2，3，4，5]，训练batch为32个，epoch为30次，经过K折交叉验证，对于不同隐层结构互信息堆叠稀疏自编码器的训练损失如图9所示。由图中可以看出不同隐层结构都可以保持收敛效果，当隐层数目取得3层效果最优，且训练数据损失迭代较快，为保证采用3层隐层自编码结构的有效性，将互信息深度稀疏自编码器在测试数据上进行重构误差测试，结果如图10所示。因此本文采用堆叠稀疏自编码器隐层数目为3层。构建互信息堆叠稀疏自编码器结构为[7，20，20，20，7]，其中7代表输原始数据维数，20代表隐层神经元数目。搭建深度稀疏堆叠自编码器，其内部隐含层由预训练好的互信息堆叠稀疏自编码器构成，深度堆叠稀疏自编码器结构和各层参数设置如表1所示。图11表明互信息深度堆叠稀疏自编码器训练数据重构误变化曲线差经过微调很快达到收敛效果，且保持较低误差。误差收敛的原因在误差梯度下降算法有效性和采用多层的自编码结构在一定程度上可以映射出原始数据更加丰富的多维度非线性特征，尤其对于工业高维度、高噪声数据，其数据深度特征提取尤为重要，保持较低的重构损失在于稀疏项的对噪声抑制能力以及本文引入互信息权重因子保留用于建模的高质量特征参数。

图11 互信息深度堆叠稀疏编码器微调训练损失Fig.11 Fine tuning training loss of mutual information deep stacked sparse encoder

表1 互信息深度堆叠稀疏编码器结构Table 1 Mutual information deep stack sparse encoder structure

图9 不同隐层互信息堆叠稀疏编码器训练损失Fig.9 Training loss of stacked sparse auto-encoder with different hidden layer based on mutual information

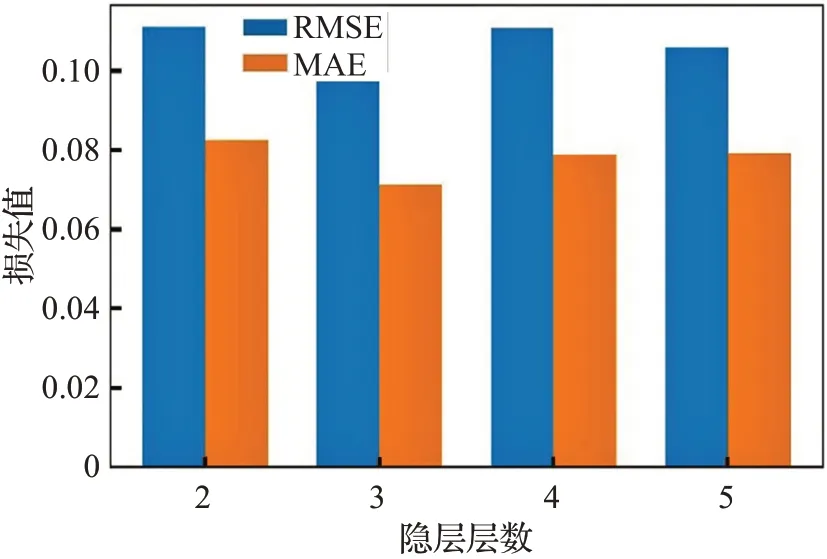
图10 不同隐层互信息堆叠稀疏编码器测试数据重构误差Fig.10 Reconstruction error of testing dataset of stacked sparse encoder with different hidden layers

将上述预训练好的堆叠稀疏自编码器进行深度堆叠，将其中的隐层进行迁移抽取微调，得到互信息深度堆叠稀疏自编码器。

在本实验中，参数的选择使用贝叶斯调参方法，每次实验选取一组参数用来矫正后验概率的评估，且贝叶斯调参每次迭代过程会融合上次参数信息，具有迭代速度更快。确定DLSTM的网络层如表2所示，网络第一层和第二层都为Bi-LSTM，其中每层LSTM输出单元个数为4，第三层为单向LSTM，其输出神经元个数为4，最后连接全连接层连接预测输出。时间窗大小设为5，每个时间窗内包含7个影响因素和窗口内最后时刻的丁烷C4含量。

表2 DLSTM模型结构Table 2 DLSTM model structure

4.3 实验仿真验证

实验首先基于原始数据进行建模，为了验证DLSTM的模型性能，本文同时引入RNN、LSTM、GRU等方法与本文提出的DLSTM方法进行对比，预测误差如表3所示。

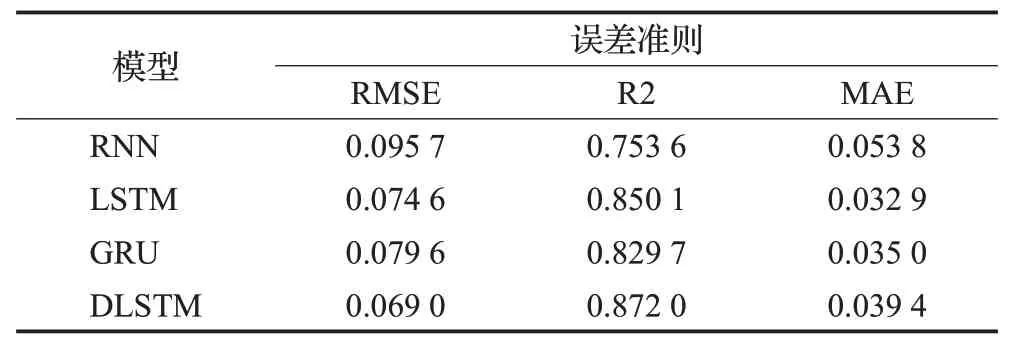
表3 不同方法预测结果Table 3 Prediction results of different methods

从表3可以看出，DLSTM模型具有更好的预测性能，RMSE值 为0.069 0，R2值 为0.872 0，MAE值 为0.039 4，在其他对比的方法中，LSTM模型预测误差RMSE值为0.074 6，R2值为0.850 1，MAE值为0.032 9。图12给出了不同模型真实变化曲线与预测曲线的对比效果。其中，RNN和L-STM的预测效果较差，在小波动预测细节上并未表现出良好的预测性能，对于C4含量较大波动情况总出现预测值偏差较大，而GRU方法对预测峰值波动变化较大的情况时，不能较好地预测C4含量的突变趋势，DLSTM模由于融入Bi-LSTM双向记忆细胞单元，将输入的序列数据进行双向并进行深度提取，融合多层信息模型表现出更好的预测性能。为了验证本文互信息深度堆叠稀疏编码器的编码特征效果，本文现将MI-DSSAE互信息深度堆叠稀疏编码器与上述方法进行结合，不同方法预测误差如图13所示。当预测值分布在红线周围是较为理想的预测结果。

图12 不同模型真实曲线与预测曲线对比Fig.12 Comparison of real and predicted curves in different models

从图13得出，MI-DSSAE-RNN、MI-DSSAE-GRU和MI-DSSAE-LSTM等模型的预测值大多数位于红色拟合线真实值的单侧，带来较大预测误差，而MI-DSSAEDLSTM模型的预测值较多能够聚集在真实值左右附近，即更多预测值落在拟合红色直线上，表现出更准确的预测性能。最后，本文将上述所有的方法进行对比，结果如表4所示。从表4结果可以得出经过MI-DSSAE网络对数据特征提取比未加特征提取的预测模型预测的准确度高，相比原来相同的预测方法有着不同程度的提高，其中MI-DSSAE-RNN的RMSE误差指标方法降低32.8%，MI-DSSAE-GRU的RMSE误差指标降低19.5%，MI-DSSAE-LSTM的RMSE误差指标降低5.6%，本文提出的MI-DSSAE-DLSTM建模方法的误差指标在所有对比方法中达到最优，RMSE误差为0.046 7，R2值为0.941 4，MAE值为0.032 2。

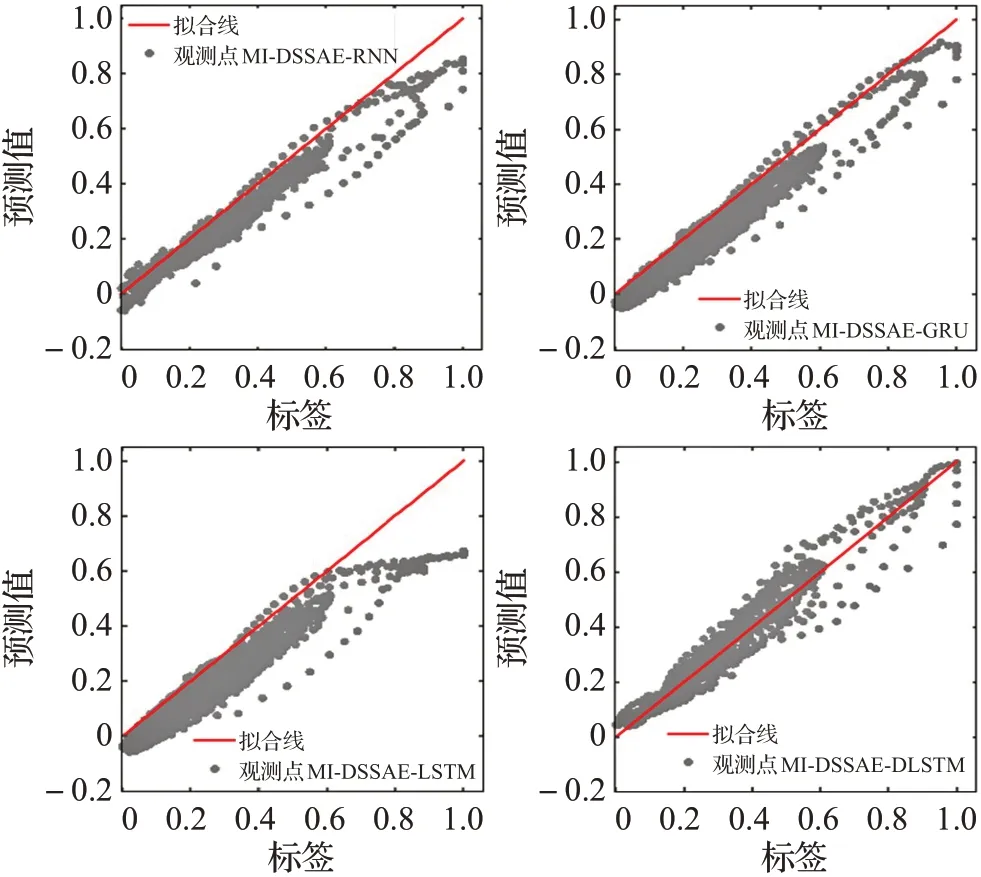
图13 结合MI-DSSAE编码的不同预测模型结果对比Fig.13 Comparison of results of different prediction models combined with MI-DSSAE encoding

表4 不同模型预测误差对比表Table 4 Comparison of prediction errors of different models

5 结束语

本文为了解决流程化工业生产中由于各个参数变量之间存在相互影响和动态变化特性，针对序列数据预测关键变量精度下降问题，首先对多变量动态序列数据提出一种深度堆叠稀疏编码器结构的深度特征提取模型，为保证提取特征的有效性，加入互信息权重因子对损失函数进行限制，对于提取的隐含深度特征信息，建立深度长短记忆DLSTM模型，充分捕捉动态数据的变化特性，并进行预测。通过脱丁烷塔实际工业案例进行模型验证，为增加方法对比性和有效性，引入RNN、GRU、LSTM以及MI-DSSAE-RNN、MI-DSSAE-GRU、MI-DSSAE-LSTM与本文模型进行对比，本文模型表现出较好的预测精度，为工业流程化生产时的监控预测提供有效方法和参考方案。