有限线法及其在流固域间耦合传热中的应用*

高效伟 丁金兴 刘华雩

(大连理工大学航空航天学院,工业装备结构分析国家重点实验室,大连 116024)

本文创建一种全新的数值计算方法—有限线法,并将其用于求解流体-固体一体化耦合传热分析.常用的有限元法是基于体单元的离散方法,有限容积法是在控制体面上运算的方法,边界元法是在边界面上离散的方法,无网格法等是由计算点周围的散点构建计算格式的方法.本文提出的有限线法是一种基于有限条线段离散的方法,在每个点只需要两条或三条直线或曲线构成的线系,则可建立任意高阶的算法格式.创新性思想是: 通过采用沿线段求方向导数的技术,由一维拉格朗日插值公式,建立二维和三维问题的任意高阶线系的空间导数,并以此直接由问题的控制偏微分方程与边界条件建立离散的系统方程组.有限线法理论简单、通用性强,能以统一的格式求解固体与流体力学等偏微分方程边值问题.在流体方程中,扩散项采用中心线系保证高精度计算,而对流项则采用迎风线系体现其方向性特征.本文将给出有限线法求解流固耦合传热问题的几个算例分析,验证其正确性与有效性.

1 引言

根据算法离散与操作维度的不同,常用的数值计算方法可归纳为4 类: 基于体单元的计算方法(如有限元法[1,2]、有限块法[3,4]、单元微分法[5,6]等),基于面单元的方法(如有限容积法[7,8]、边界元法[9,10]、边界面法[11]等),基于线单元的方法(如有限元线法[12]、交叉线法[13]等),以及基于散点计算的方法(如无网格法[14-16]、基本解法[17]、奇异边界点法[18]等).

在基于体单元的计算方法中最具代表性的方法是有限元法(FEM).用其分析问题时将计算域划分成有限个体单元,物理量的表征、微分是通过与计算域维度一样的体单元实现的.鉴于其强大的解题能力,FEM 已被用于解决各种工程问题,特别是固体力学问题,这主要归因于其使用了具有良好性能的等参单元进行几何离散和物理量插值[19],使得计算结果非常稳定.此外,FEM 所需要的单元和节点数远少于有限容积法(FVM)和有限差分法(FDM).FEM的弱点主要体现在: 1)需使用变分原理或虚功原理来建立计算格式,对于不同的问题所建立的表达式不同,从而不便于建立多场耦合问题的统一算法;2)用传统的FEM 求解含有对流项的问题时,不易实施迎风格式与激波捕捉计算.为此,近年来间断伽辽金有限元法(DGFEM)在流体力学中得到了快速发展[20],其在每个单元内用独立定义的节点进行高阶函数逼近,因而可以较容易实现迎风计算,然而DGFEM 计算效率很低,此外如果单元内有激波的存在,内部间断使得收敛性和鲁棒性大幅下降.

面单元计算方法是指主要在面上进行运算的方法.将FVM 归入面单元计算方法在维度上似乎不太协调,但是科学的.这是因为FVM 是一种将问题的控制微分方程的守恒形式(全微分形式)使用高斯散度公式将控制体积分转换成在控制体面上进行积分运算的算法[7].FVM 是一种通量守恒性最好、激波间断面最容易捕捉的数值方法,也由此成了目前计算流体力学中的主流方法.BEM 是一种典型的面单元计算法,是通过两次分部积分和使用高斯散度公式,并取权函数为问题基本解而形成边界积分方程的算法.BEM 几何离散简单,能很好地模拟断裂力学中的应力集中现象,并能有效求解无限域与半无限域问题[21].BEM的弱点是在求解有源(热源、体积力、化学反应生成项等)、非线性、非均质问题时,会有域积分出现在积分方程中,削弱了其只在边界上离散的优点.

基于线单元的计算方法笼统地讲可以包括有限元线法[12]以及梁单元、杆单元[22]等的算法.前者是借助于能量泛函的变分,将控制偏微分方程半离散化为用结线表示的常微分方程组求解法,而后者则是通过一维离散模拟具有一维维度的构件的方法.真正通过线单元的离散实现高维(二维和三维)问题的微分方程的求解方法是作者最近提出的交叉线法(CLM)[13].该方法通过在每个点建立由两条(二维问题)或三条(三维问题)相交的线段,并通过形函数构造法建立多维问题的形函数,然后采用微分法则,导出各阶偏导数计算式,最后将其代入控制微分方程与边界条件,建立问题的离散系统方程组.CLM 属于配点型的强形式计算方法,目前是通过单元的形式在自由单元法中使用[13],用到的线系可以是直线,也可以是曲线.因而,该方法具有几何离散简单、适应性强、编程方便、系数矩阵稀疏等特点,是一种具有开发潜力的计算方法.然而,根据单元形函数构造法(即满足Delta符号性质的解[13])很难构造三阶及其以上的形函数,这给流体力学中经常用到高阶格式的算法带来了限制.

基于散点的计算方法有无网格法(MLM)等[14-18],该类方法不需要有规则节点分布的单元,只需一些任意分布的散点则可建立解题算法.MLM的形函数及其偏导数是通过最小二乘法等技术在一定范围(紧支域)内的点集构建的.基本解法与奇异边界点法等则是通过问题微分算子的基本解在虚拟边界或真实边界节点上配置方程进行求解的.MLM在几何适应方面具有独特的优势,因而在复杂几何模拟与动边界问题方面得到了广泛的应用.MLM虽然有使用灵活、几何适应性强的优点,但也有计算效率低、结果稳定性差以及不易施加边界条件与各向异性物性的弱点.

值得介绍的一种新的配点型方法是作者近年来提出的自由单元法(FrEM)[23,24].该方法吸收了FEM 与配点型MLM的优点,即: 在函数表征方面,采用FEM 中有规则节点分布的等参单元,因而具有几何适应性强、计算效率高、结果稳定性好、容易施加各向异性物性以及边界条件的优点;在算法方面,采用配点法技术,直接由控制方程与边界条件逐点产生系统方程.FrEM 在每个点只需要一个和周围自由选择的节点形成的独立的等参单元,因而不需要考虑物理量在单元之间的相互连接关系以及导数连续性问题.此外,单元的自由性也使其更容易构造高阶迎风格式计算流体力学方程中的对流项.FrEM 已在固体力学[25]、流体力学[24]与传热学[26]中得到了成功的应用.然而,由于高阶自由单元是由结构化节点形成的[23],因此三维问题的高阶单元需要较多的节点,这给几何建模与数据存储带来了很大的不便.

本文在作者多年来研究BEM、FEM、配点型MLM 等方法的基础上,提出了一种全新的数值方法—有限线法(FLM)[27].该方法在每个点只需要1—3 条交叉线段(称为线系)则可建立一维到三维问题的算法格式.由于每条线段用拉格朗日多项式插值公式构建函数表征关系,因而可以很方便地建立任意高阶的算法.FLM 具有CLM 和FrEM的全部优点,还有类似于FDM 容易使用的性能,并有高阶线系所用节点少、容易施加不同物性与边界条件、以及容易构建迎风格式的特点,因此既适合于求解流体力学问题、也适合求解固体力学问题.

一些现代装备结构,如发动机涡轮等,一直处于高温服役环境,因而使用冷却技术提高其耐高温能力是经常使用的重要手段,结构内部设置冷却通道是最常用的热防护形式,对其进行流体域-固体域间耦合传热分析是结构设计的重要依据.本文将系统介绍FLM 在求解冷却通道结构流固域间耦合传热方面的应用,为现代装备结构设计提供有力的分析手段.

2 流体与固体中的传热偏微分方程边值问题

流体与固体中的热传导微分方程可统一表示为[5,24]

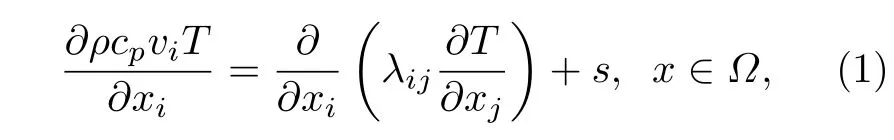
式中,ρ为流体密度,cp为定压比热,vi为流速,T为温度,λij为导热率,s为热源;式中的重复指标表示求和,Ω为计算域,对于固体vi为0.(1) 式中的左端为对流项,右端第一项为扩散项[7].

相关的边界条件可表示为

其中,∂Ω为Ω的边界,ni为边界外法线方向矢量,h为换热系数,T∞为环境温度.

从 (1)—(4) 式可以看出,控制微分方程与边界条件涉及到的关键项是温度对空间总体坐标的一阶与二阶偏导数,本文将用有限线法建立各阶偏导数计算式.

3 计算空间偏导数的有限线法

作者在文献[5]中导出了一般拉格朗日等参单元形函数对总体坐标的偏导数解析表达式,但可以证明其一阶偏导数只与通过计算点的交叉线上的节点有关[13],因此本文采用交叉线系建立各阶空间偏导数计算式.

3.1 交叉线系的建立

本文提出的FLM 是一种配点型的计算方法,计算时与FDM 和MLM 类似,首先通过网格生成技术[28],将计算域划分成一系列配置点(CP),图1给出了一个二维问题的节点划分示例.

图1 将计算域划分成一系列配置点Fig.1.Discretizing computational domain into a series of collocation points.

然后,对每个CP,建立由两条(二维问题)或三条(三维问题)线段组成的交叉线系.图2 和图3分别展示了一个内部点的二维(d=2)和三维(d=3)的交叉线系.原理上,线系中的线段相互间越垂直计算精度越高,但只要不共线(二维线系)和不共面(三维线系)则可获得满意的结果.

对于位于边界和角点上的CP,则需要将图2和图3 中的交叉点移到边界和角点上,具体做法可参见文献[13].

图2 两条线组成的二维(d=2)线系Fig.2.Line set of 2D (d=2) consisting of two lines.

图3 三条线组成的三维(d=3)线系Fig.3.Line set of 3D (d=3) consisting of three lines.

3.2 基于线系的空间导数计算公式

在线系的每一条线上,定义m个节点(如图2和图3 所示),并由下列拉格朗日多项式插值公式表达坐标x与物理量u的函数变化关系[5,23]:

式中,l为从节点1 开始计算的线段长度,uα为第α个节点的u值.Lα为拉格朗日多项式插值函数:

其中,lα为第α个节点的长度.以二维线系为例,标记函数u对总体坐标xi的一阶偏导数分量为∂u/∂x1和∂u/∂x2,则沿线段l的方向导数∂u/∂l可表示为

对于每一条线可建立一个上述方程,当d条线考虑后可得到如下的矩阵方程:

对(9)式求逆,并考虑到(6)式,则可得如下的分量表达式:

为了方便使用,可将(11)式简写为

式中,重复指标α表示对M1个节点求和,xc表示线系中各线交叉处(即配点)的坐标称为一阶导数算子.需要说明的是,矩阵J是一个2×2 或3×3的矩阵,可以很容易求得其逆矩阵的解析表达式.

对于二阶导数,可以在一阶导数公式上再次作用导数算子,得到:

需要说明的是,(13)式与(15)式中重复指标α求和的节点数量是不一样的.图4 展示了一个配置点(节点3)采用5×3 线系离散中,一阶导数相关的7 个节点(由实心点标记的节点)与21 个二阶导数相关的节点(由实心点+空心圆点标记的节点)的示意图.对于更高阶的导数算子可由类似的递归方法形成[27].

图4 一阶与二阶导数相关的节点Fig.4.Related nodes of the 1st and 2nd order partial derivatives.

4 流固耦合传热问题中的有限线法公式

将空间导数计算公式(13)和(15)直接代入流固耦合传热方程(1)及其边界条件(2)—(4),则可建立耦合问题的代数离散方程.不过,流体传热方程中存在对流项,需要用迎风格式才能精确求解,而扩散项用中心格式才能得到稳定的计算结果.本研究通过采用两套线系的技术解决此问题,即使用迎风线系体现计算点上游对其的影响,用中心线系保证扩散项的稳定性与精度.图5 展示了采用5×4 节点线段形成的两套线系的节点分布,其中红色的节点属于中心线系(central line set),黑色的属于迎风线系(upwind line set).

图5 同一配置点的迎风与中心线系Fig.5.Upwind and central line sets at a same collocation point.

采用 (13) 式和(15) 式可将方程(1)—(4)离散成下列形式:

式中分别为基于迎风线系和中心线系计算的导数算子,其中的q为

耦合计算时,将流体域与固体域进行一体化离散.对于固体域,(17)式的第1 个方程中的第1 项(对流项)为0.

将上述方程中的配置点xc作用于流体域与固体域的所有配置点,并在流-固界面上使用下列温度协调条件与通量平衡方程(其中上标f 与s 分别代表流体与固体):

则可形成如下的一体化分析矩阵方程:

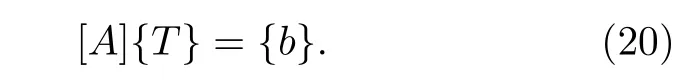
求解上述方程则可获得所有节点的温度值.需要说明的是,由于每个配置点的线系所涉及到的节点数比传统的数值方法FEM 和FVM 少得多,因此 (20) 式中的系数矩阵A是一个非常稀疏的非对称矩阵.

5 算例分析

根据本文所推导的公式,采用FORTRAN 语言编制了有限线法程序,程序中采用了分区技术[28],可对复杂问题进行计算分析.下面对现代高温装备中经常使用的冷却管道结构中的一些流固域间耦合传热问题进行分析,用以验证本文所述方法的正确性与有效性.计算中,每个配置点的每条迎风线用二阶精度,中心线用四阶精度.

5.1 单根管道结构流动传热分析

本文的第一个算例是用于验证本文提出的FLM的正确性与有效性.算例的几何尺寸与边界条件如图6 所示,管道的上下外表面处于环境温度为900 K的对流换热环境中,流固界面的换热系数为1100 W·(m2·K)—1,流体域的物性为:λ=0.6 W·(m·K)—1,ρ=1000 kg/m3,cp=4200 J·(kg·K)—1;固体域为λ=200 W·(m·K)—1.

图6 单根管道结构尺寸与边界条件Fig.6.Dimensions and B.C.of a single channel structure.

为了提供参考结果进行比较,本文用FLUENT软件采用较为稠密的网格对该问题进行计算,其中在x方向(水平方向)和固体域,网格为等间距分布,流体域靠近壁面网格逐渐加密.在x方向划分了151 个点,在垂直方向: 固体域20 个点,流体域40 个点.

5.1.1 FLM 使用均匀网格的网格收敛性分析

首先基于均匀网格对该问题进行FLM 计算分析,考察其网格收敛性.计算发现,结果只对流体域中的垂直方向的网格敏感.因此,在FLM 计算中,在x方向流固域都使用51 个点;在垂直方向,固体域使用7 个点,流体域分别使用21、41 和71 个点进行计算,这3 种情况分别标记为FLMfine1,FLM-fine2 和 FLM-fine3.图7 和图8 分别给出了流速为v=1 m/s 时3 种网格的计算结果.可以看出,网格FLM-fine3 收敛到了FLUENT的计算结果.此外,变化趋势显示,FLM 具有很好的网格收敛性.

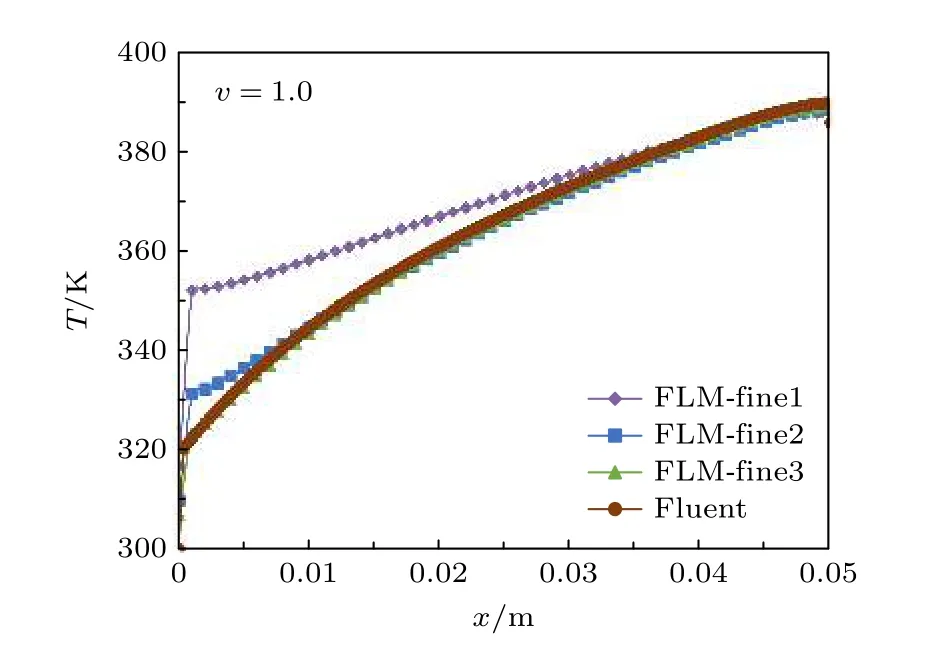
图8 不同网格尺寸下流固界面温度分布Fig.8.Temperature distribution on the fluid-solid interface under different mesh sizes.

从图7 可以看出,温度为300 K的流体流过冷却通道后,可以将处于900 K 热环境的结构外表面温度降低到400 K 以下,充分说明了高温结构中采用主动冷却管道的冷却效果.

图7 不同网格尺寸下管道外表面温度分布Fig.7.Temperature distribution on the channel outer surface under different mesh sizes.

5.1.2 使用比例间距网格计算

为了考核FLM 在非均匀网格中的表现,在上述FLM-fine1的网格中,允许流体域与固体域的计算点从各域边界到其中线按比例变化,相邻间距比例因子在水平与垂直方向分别为1.2 和1.5.图9展示了流固域左端与中间部分的FLM 线系连成的局部网格图.图10 和图11 分别为不同流速下管道外表面和流固界面的温度沿x方向的分布曲线.为了比较,也绘出了用同等节点数但等间隔分布的网格的计算结果(FLM-uniform).

图9 管道结构左端与中间局部网格放大图Fig.9.Enhanced meshes of the left and middle parts of the channel structure.

可以看出,用比例间距的计算结果 (FLM-ratio)与Fluent的计算结果吻合的很好,而用等间隔网格的计算结果(FLM-uniform)在如此少的节点数下的计算结果不可接受.可见,在FLM 计算中,采用不等间距网格可以大量减少所需的节点数.不过,从图10 和图11 中的v=0.1的结果可以看出,对于流速慢的情况,即使用等间距网格也可以获得满意的计算结果.

图10 不同流速下管道外表面温度分布Fig.10.Temperature distribution on channel outer surface under different velocities.

图11 不同流速下流固界面温度分布Fig.11.Temperature distribution on fluid-solid interface under different velocities.

5.2 多根管道结构流动传热分析

本文的第2 个算例是含有3 根管道的冷却结构,如图12 所示.三根管道的直径均为2 mm,其中,中间管道具有5.7°的倾斜角.整个冷却结构的左、右边界除了流体的入口温度Tin部分外其他部分均为绝热边界条件(q=0).三根管道中的流体的密度与比热与算例5.1 中的一样,均为ρ=1000 kg/m3与cp=4200 J·(kg·K)—1.计算中,整个冷却结构分为7 个计算域,其中第2,4,6为流体域,其他为固体域.几何离散中,所有域沿水平方向(x方向)划分为等间隔的101 个点,沿垂直方向划分为从各域壁面到其中线间距比例因子为1.2的31 个点.图13为FLM 分析中由所有线系连成的网格图,注意到由于中间管道的倾斜使得计算域3—5的网格都成了非正交网格.

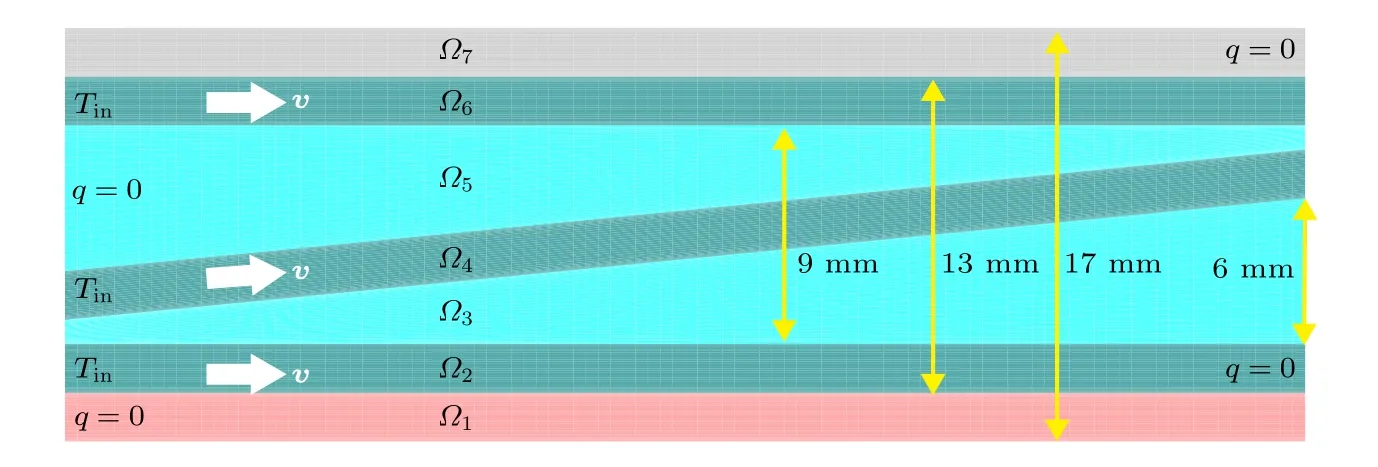
图12 三根管道结构尺寸与边界条件Fig.12.Dimensions and B.C.of a three-channel structure.

图13 三管道结构FLM 分析线系连成的网格图Fig.13.Mesh connected by line sets of all points for FLM analysis of the three channel structure.

5.2.1 流、固域采用相同条件的计算分析

首先考察整个管道结构处于与算例5.1 所示的外部环境与边界条件,即上下外表面所处的环境温度为T∞=900 K,换热系数为h=1100 W·(m2·K)—1,流体与固体的导热系数λ 以及流体域的入口温度Tin与算例5.1 中的相同.图14为在不同流速下整个冷却系统的温度云图,图15为上部外表面温度变化曲线,而图16为斜管流体域下表面的温度变化曲线.

从图14 可以看出,不同流速下冷却系统中间部分的温度变化很大.当流速很低时(如v=0.002 m/s的情况),只有流体的入口部分能得到冷却;随着流速的增加,冷却效果越来越明显;当流速为v=0.5 m/s 时,整个中间结构都能得到冷却.另外,从图16 和图14(d)可以看出,当流速为v=0.5 m/s时,斜管流体域下表面的温度基本为流体的入口温度,说明在此流速下不需要中间的冷却管道对结构进行冷却.

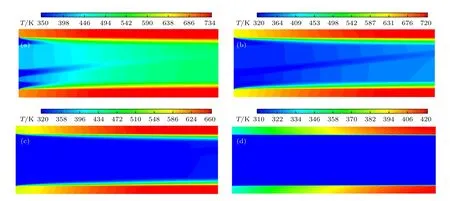
图14 不同流速下的温度云图 (a) v=0.002 m/s;(b) v=0.005 m/s;(c) v=0.01 m/s;(d) v=0.5 m/sFig.14.Contours under different velocities: (a) v=0.002 m/s;(b) v=0.005 m/s;(c) v=0.01 m/s;(d) v=0.5 m/s.

图15 不同流速下结构上部外表面温度变化曲线Fig.15.Temperature variation curve on the outer surface of upper structure under different velocities.

图16 不同流速下斜管流体域下表面温度变化曲线Fig.16.Temperature variation curve on the lower surface of fluid domain of the oblique channel under different velocities.

5.2.2 流、固域采用不同条件的计算分析

接下来将整个结构的上下表面对流换热边界条件分别设置为T∞=1000 K,h=800 W·(m2·K)—1和T∞=700 K,h=1100 W·(m2·K)—1;各计算域的导热系数λ、流体域的入口温度Tin和流速v如表1所示.图17为计算得到的整个冷却系统的温度云图,图18 给出了冷却系统上表面(用Upper-surface标记)、下表面(Lower-surface 标记)、和各区域界面上的温度沿x方向的变化曲线,其中Interface 45 表示计算域4 与5的界面,其他类推.

表1 各计算域的材料参数与入口边界条件Table 1.Material parameters and boundary conditions of each computational domain.

从图17 可以看出,冷却通道附近的温度与冷却流体的温度接近,说明冷却流体带走的热量明显.另外,从图18 可以看出,入口(x=0)处上下外表面的温度与环境温度具有较大的差别,这说明冷却流体可以显著地降低结构的表面温度,这是高温装备通常使用主动冷却热防护的主要原因.

图17 计算得到的管道冷却系统温度云图Fig.17.Contours of computed temperature over the channel cooling system.

图18 计算得到的冷却系统上下表面和各区域界面的温度变化曲线Fig.18.Variation curve of the computed temperature on the upper and lower surfaces as well as on the interfaces of the cooling system.

5.3 三维三管道结构流固域间耦合传热分析

本文分析的第3 个算例是含有3 根管道的三维冷却结构,如图19 所示.管道的尺寸均为1.333 mm×0.667 mm.上下表面的温度分别给定为T1=600 K 和T2=350 K.计算中,整个冷却结构分为6 个计算域,其中Ω4—Ω6为流体域,其他为固体域;冷却通道内冷却液的入口温度Tin和流速v见表2,流体的密度与比热均为ρ=1000 kg/m3与cp=4200 J·(kg·K)—1.

图19 含三根管道的三维冷却结构尺寸与边界条件Fig.19.Dimensions and B.C.of a 3D cooling structure with three channels.

表2 三维流固结构各计算域的材料参数与边界条件Table 2.Material parameters and boundary conditions of each computational domain.

图20为FLM 计算用的网格图,总共有172789个配置点,其中沿管道走向(x方向)划分了31 个点,靠近壁面的网格间距比例因子为1.2;各域沿垂直方向(z方向)均划分为11 个点,壁面比例因子为1.5;沿横向(y方向),除上下盖板的外伸部分为25 个点外,其他部分均为21 个点,壁面比例因子均为1.5.图21为横截面网格与局部放大图,可以看出下盖板的外伸部分是曲面,而且靠近右下角的网格极度非正交.

图20 所有配置点的线系连成的网格Fig.20.Mesh connected by line sets of all collocation points.

图21 横截面上的配置点线系连成的网格与局部放大图Fig.21.Mesh connected by line sets on the transverse section and a locally refined part around a corner.

图22 是计算得到的总体结构上的温度云图,而图23 是通过三根通道中线的垂直面上的温度云图.图24 和图25 分别为沿图22 所示的线段L1与L2上的温度分布.为了比较,也用商业有限容积法软件FLUENT 和有限单元法软件COMSOL 对该问题进行了计算,使用的网格是达到网格收敛下的网格.对比可以看出,FLM 计算结果与其他两种方法的结果吻合的很好,证明了本文方法在使用非规则网格方面的正确性,这是传统的有限差分法难以实现的.另外,表3 列出了采用3 种方法计算该问题时所用的节点数与时间的比较.其中,COMSOL只列了一种网格的结果,因为网格稍微密一点时计算不收敛,试算发现这主要是因为流体与固体的导热系数相差较大所致.从表3 可以看出,在同等精度下FLM 需用的网格数最少,消耗时间也较少;COMSOL 用的时间最多,而且在流体入口处附近与其他两种方法的结果有较大的差别,稳定性也差,这也许是有限单元法在处理流体相关问题中存在的固有弱点[20].此外,FLM 与FLUENT 用粗、细两种网格算的结果基本一样,说明二者有很好的稳定性.

图22 总体结构上的温度云图Fig.22.Contour plot of computed temperature over the entire structure.

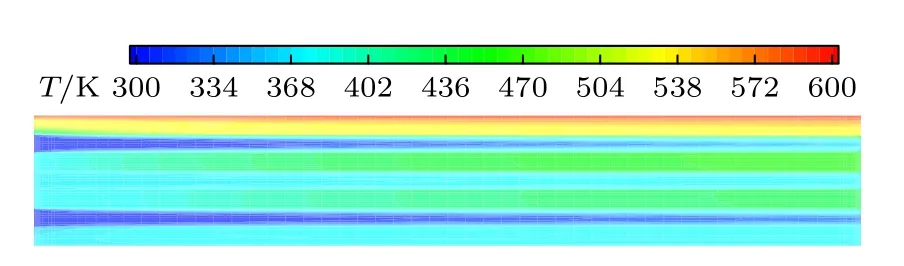
图23 管道走向垂直中面上的温度云图Fig.23.Contour plot of computed temperature over the vertical middle plan.

图24 沿图22 中所示的线段 L1 上的温度分布Fig.24.Computed temperature along line L1 marked in Fig.22.

图25 沿图22 中所示的线段 L2 上的温度分布Fig.25.Computed temperature along line L2 marked in Fig.22.

表3 三种计算方法的节点数与计算时间比较Table 3.Comparison of total number of nodes and computational time for three methods.

6 讨论与结论

论文提出了一种全新的数值计算方法—有限线法,并将其应用于求解流体域与固体域之间的耦合传热问题,根据算法的理论与在冷却通道结构中的算例分析,可以得出如下的结论:

1)本文通过线段方向导数建立的求导公式可以用统一的格式计算多维问题的任意高阶的空间偏导数;

2)创建的有限线法是一种配点型计算方法,其用法与传统的有限差分法一样方便、灵活,而且能模拟曲的和不规则的几何形状;

3)有限线法可以直接由问题的控制微分方程和边界条件建立系统方程组,不需要变分原理、能量原理及其他需要积分的数学操作;

4)本文虽然以流固耦合传热问题为研究背景,但导出的公式也适用于求解其他工程问题的偏微分方程边值问题,是一种通用的数值计算方法;

5)因为有限线法是一种强形式的计算方法,通常需要采用高阶线系计算,经验表明,采用四阶精度的中心线系和二阶精度的迎风线系可以获得高精度和高效率的计算结果;

本文所述方法是关于空间偏导数的离散的方法,考虑的控制方程是不含时间项的定常问题,但所导出的公式也同样适用于含有时间项的非定常问题,此时,时间项可采用成熟的方法进行离散[24].