基于响应面法的C型金属封严环优化设计及其蠕变疲劳寿命计算

吴新洲 ， 徐义华 ， 杨 蓓 ， 力 宁 ， 冀疆峰 ， 王 曦 ， 吴 涛

（1. 中国航发集团长江动力有限公司，湖南 岳阳 414022；2. 南昌航空大学 飞行器工程学院，南昌 330063；3. 中国航发湖南动力机械研究所，湖南 株洲 412000；4. 江西中发天信发动机科技有限公司，南昌 330096；5. 江西澳科新材料科技股份有限公司，江西 宜春 336027）

0 引言

随着现代航空发动机性能的不断提升，发动机内部工作环境更加苛刻和复杂，如高温、高转速、高压、高摩擦、高频振动等。封严装置作为发动机的重要组成部分之一，对改善发动机效率和保证发动机安全工作起着极其重要的作用[1-2]。传统静封严技术如平垫片封严、橡胶封严等，因其材料难以适应发动机苛刻的环境，因此弹性金属封严技术应运而生。弹性金属封严环有多种结构形式，如C型、W型、波纹多W型以及其他异型金属封严环[3-4]。大部分金属封严环由镍基高温合金制造而成，能很好地适应高温工作环境。

对于金属封严环的研究，国外起步于20世纪80年代，至90年代已相当成熟[1-2]。由于国外技术的封锁，我国在21世纪初期才开始对该项技术进行研究，但大多集中在W型密封环的研究。例如，王晨希等[5]研究了W型金属密封环的压缩量与压紧力的关系，分析了加卸载过程中合金基体与银层的等效塑性应变分布情况和密封机制；何少飞等[6]研究了W型封严环表面粗糙度对泄漏量的影响，建立了不同表面粗糙度下的泄漏通道模型；陈希[7]提出了一种新型多弯道W型封严环设计方案；李萍等[8]将最大Von-Mises 应力、最大接触应力、平均接触应力、回弹率作为优化目标，构造二阶响应面近似模型，利用NSGA-II算法对W型密封环进行了多目标优化研究；龚雪婷等[9]对金属W型密封环在给定工况下的弹塑性接触变形进行非线性有限元分析，得出相应情况下的接触应力分布和Von-Mises应力分布；文献[10-11]研究了密封环结构参数、波层和温度对密封环轴向刚度和泄漏量的影响规律；李伟平等[12]应用有限元与CFD方法研究了W型封严环泄漏与接触应力模型。

C型封严环结构较简单，主要用于高压轴向形变小的小体积腔室[13]，一般有内压型和外压型两种基本形式，属于静封严，允许有少量的泄漏。对于C型环，目前国内的研究还比较少。C型环的设计方法没有统一的标准，多数情况下，在已知安装结构尺寸的前提下，选定某个压缩量，确定C型环主要的结构尺寸，再根据个人设计经验选择材料厚度，然后应用有限元分析法计算其回弹率、刚度、最大等效应力及接触应力等。这种方法在一定程度上可能满足某些特定密封工况的要求，但其设计存在较大的偶然性，难以使C型密封环达到最优性能。

综上所述，为了建立C型环一般性的优化设计方法，本研究提出基于响应面法的优化设计方法。首先讨论各单一要素对密封性能的影响，然后基于响应面法考虑各参数耦合效应进行C型环结构优化，最后基于某型发动机工作时长2000 h大修的工作寿命，对C型环进行疲劳寿命验证。

1 影响C型环性能的关键结构参数

C型环基本结构尺寸如图1a所示，主要特征尺寸包括封严环大径D、环径d以及板材厚度t。其安装部位结构尺寸如图1b所示，一般已知安装大径D1、安装内径D2和安装高度h。

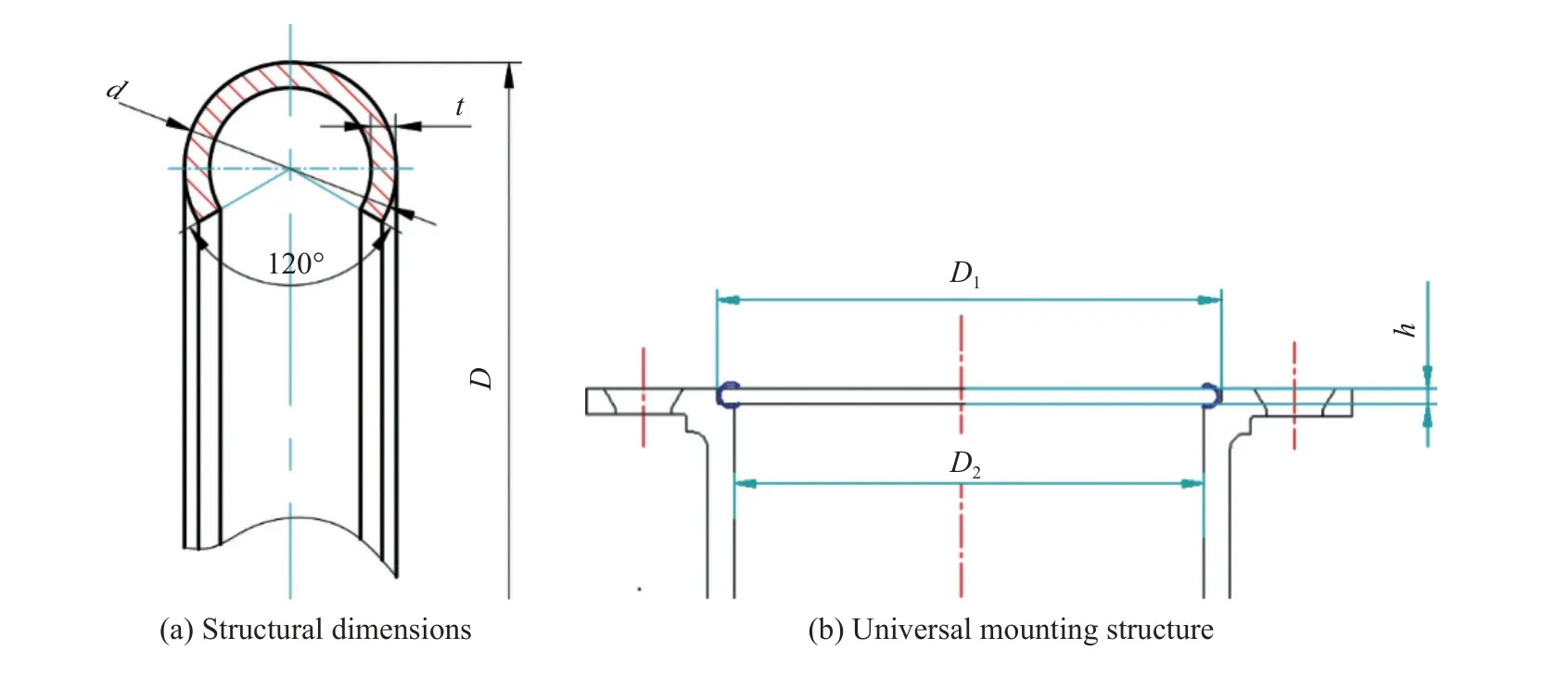
图1 C型封严环结构尺寸及通用安装结构Fig.1 Structural dimension and universal mounting structure of C-type sealing ring

依据C型环密封原理及其安装结构可知，环径d等于安装高度h和密封所要求的压缩量ΔZ之和，即d=h+ΔZ；再根据互换性要求及由于C型环因压缩引起的径向变形而保证其有效的扩展距离（图2），要求大径D应稍小于安装结构尺寸D1，即D＜D1；最后根据C型环安装在密封槽中，不允许其结构外露，C环的内径在保持压缩状态大于腔体内径的同时，还要小于自由状态开口120°范围。C型环在自由状态与安装后的工作状态之间尺寸关系如图3所示。

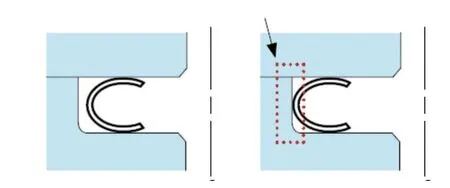
图2 保证有效的扩展距离示意图Fig.2 Schematic diagram for ensuring effective extension distance

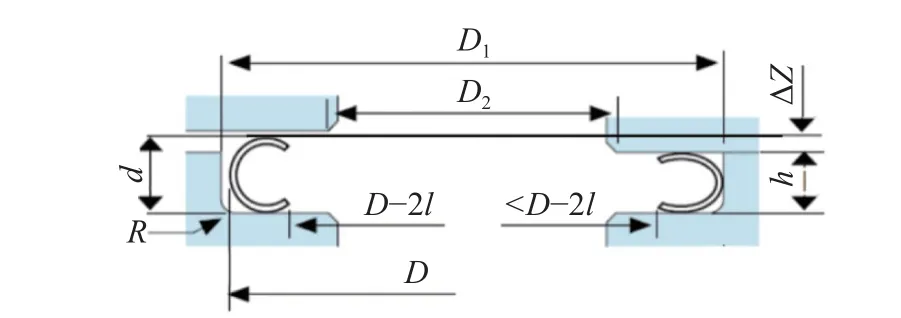
图3 C型环自由状态与安装后工作状态的尺寸关系Fig.3 Dimensional relationship between free state of C-ring and working state after installation

由以上C型环结构尺寸的设计方法可知，关键结构参数是压缩量ΔZ和材料厚度t。根据C型环性能的技术要求，即主要参数为泄漏量V和压缩回弹率η。而泄漏量与封严环工作状态下的接触应力相关，那么将压缩量ΔZ和材料厚度t作为自变量，以回弹率、接触应力和最大等效应力作为目标参数进行C型环结构优化。

2 单一因素对C型环性能的影响

2.1 计算工况

已知C型环轴向安装深度h，定义相对压缩率Z为：

参考某型发动机金属封严环的压缩量，取压缩率分别为7.5%、12.5%、17.5%及材料厚度分别为0.20、0.25、0.30 mm的条件，对结构进行优化。首先采用正交规划方法设置计算工况，研究压缩量和材料厚度对C型封严环性能的影响。

设C型环工作温度为900 K，轴向安装深度h=1.8 mm，密封压差为2.7 MPa，安装槽大径为80 mm，则取C型环外径为79.8 mm。采用正交法得到各部位安装的C型封严优化参数及工况如表1所示。

表1 C型金属封严环优化计算工况Table 1 Optimum calculation conditions of C-type metal sealing ring

2.2 各工况下C型环回弹率及应力计算

1）有限元模型。

根据封严环的工作温度，取其材料为GH4169，其力学及物理性能参见文献[14]。封严环的结构为空间三维轴对称模型，而轴对称是弹性空间的一个特殊问题，特点是物体为某一平面绕其中心轴旋转而形成的回转体。由于三维空间轴对称模型的对称性，轴对称平面中的2个位移分量x、y可以确定物体的应变和应力状态。因此，C型环结构分析可简化为二维轴对称模型。

2）边界条件及载荷工况。

边界条件：下法兰固定；上法兰施加轴向位移，即各工况下的压缩量；上、下法兰与C型密封环接触，摩擦系数设置为0.15。

载荷：预紧压缩下，只有上法兰施加轴向压缩位移，无工作压差；在工作温度下，C型密封环的内外侧施加各工况下的压差。

3）网格无关性验证。

网格尺寸对于有限元分析是重要的影响因素，网格尺寸过大达不到一定的计算精度要求，但网格过细则会导致计算效率低下。为了得到合适的网格尺寸，拟对压缩量为0.15 mm的工况网格大小的影响进行分析。网格尺寸分别选取20、15、10、5 μm。图4分别为20、5 μm的网格模型图。

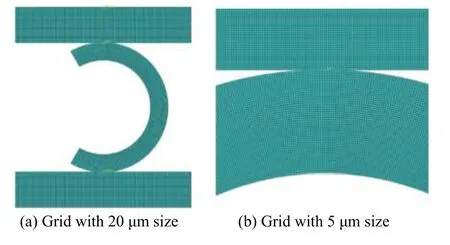
图4 网格划分示意图Fig.4 Schematic diagrams of grid

图5为4种网格尺寸的等效应力云图。由图可知，4种网格尺寸的等效应力分布基本一致，最大等效应力分别为1164、1167、1170、1172 MPa，计算结果基本一致。后续研究中，取网格尺寸为20 μm。

图5 不同网格尺寸的等效应力云图Fig.5 Equivalent stress distributions at different grid sizes

4）计算分析方法及类型。

以工况1下（即压缩量为0.15，材料厚度为0.20 mm）的常温条件为例。图6为等效应力云图，由图可知，该工况下最大等效应力为1260 MPa。图7为接触应力云图，由图可知，该工况下的最大接触应力为360.2 MPa。

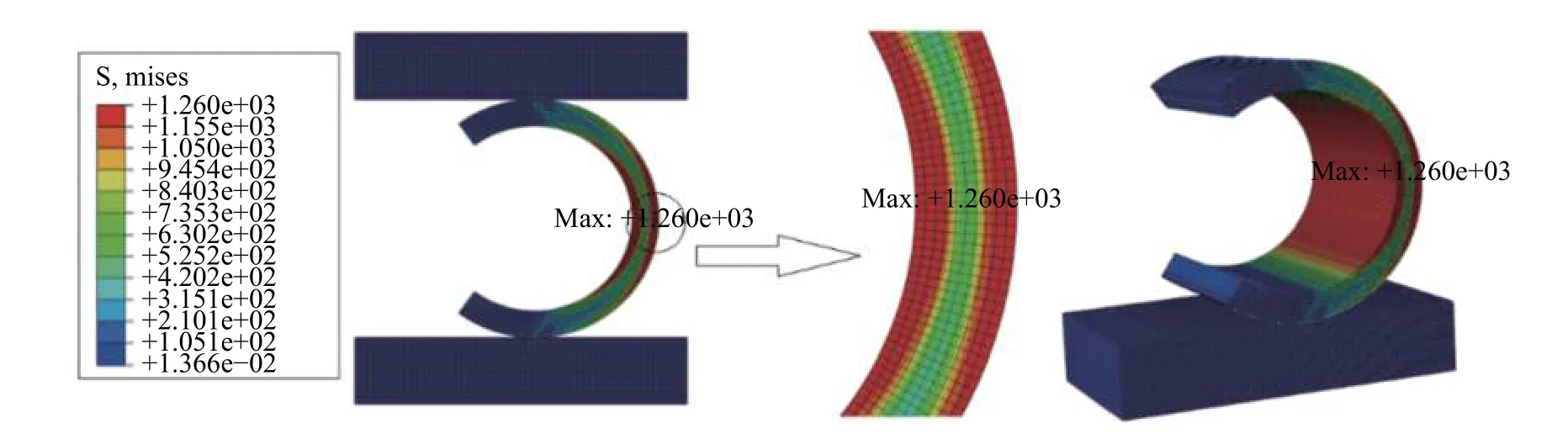
图6 常温0.15 mm压缩量的等效应力图Fig.6 Equivalent stress diagram of 0.15 mm compression at normal temperature

图7 常温0.15 mm压缩量的接触应力图Fig.7 Contanct stress diagram of 0.15 mm compression at normal temperature

图8为C型封严环压缩与回弹过程示意图。压缩起始位置C环高度为d，即C环环形直径。压缩后的环高为d-ΔZ，回弹后的环高为h2，则回弹量为h2-(d-ΔZ)，永久变形量为d-h2，即回弹率为：

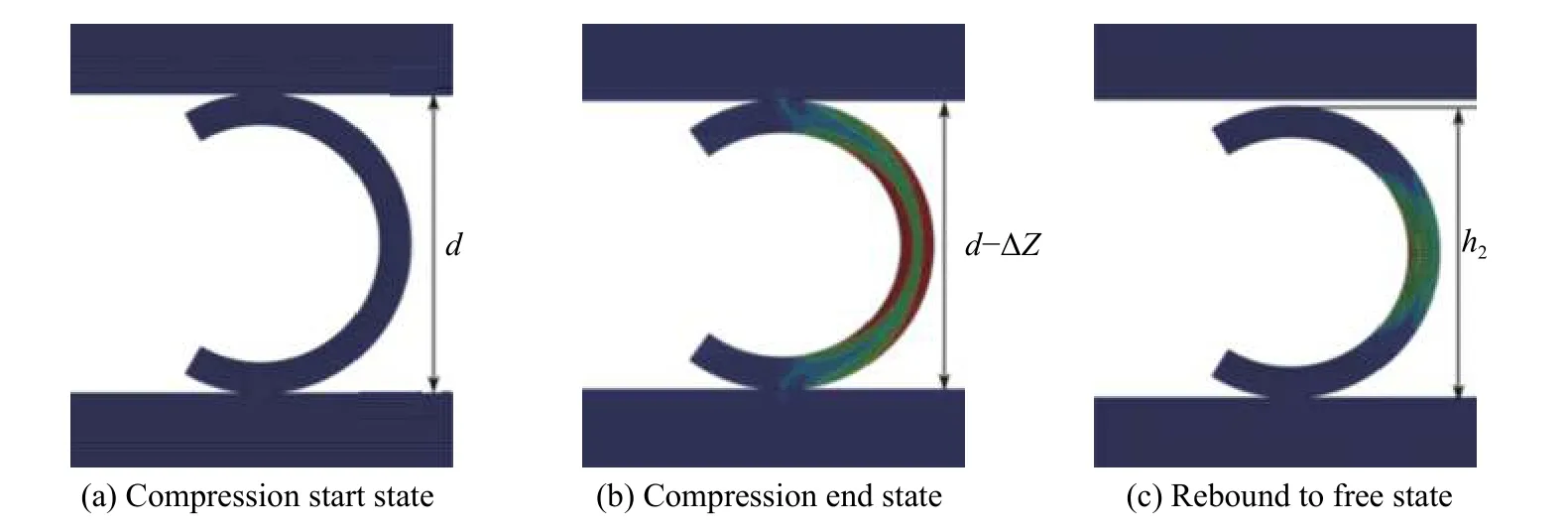
图8 C环压缩与回弹过程Fig.8 Compression and rebound processes

由式（2）计算出该工况下的回弹率为69.20%。

在C环压缩回弹过程中，上下板受到支反力RF作用。为了方便得到RF的总和，将上板面与面上一点耦合，即可在耦合点上得出整个面受到的RF总和（图9），记作F1。则刚度k为：

图9 C型环耦合点及支反力Fig.9 Ring coupling point and support reaction force

由式（3）计算出该工况下的C环刚度为2.77×107N/m。

根据以上计算及分析方法，得到各个工况下的计算结果，如表2所示。由表2可以得出各单一要素对C型封严环性能的影响。

表2 C型金属封严环各个工况优化计算结果Table 2 Optimization calculation results of C-type metal sealing ring under various working conditions

图10为压缩量及材料厚度对应力、回弹率及刚度的影响规律。由结果可以看出，在材料厚度不变的情况下，随着压缩量的增大，最大等效应力、最大接触应力随之增大。但由于随着压缩量增大，C环的弹性模量并不是个常数，其变化与材料厚度相关，即得到最大等效应力与压缩量关系线是不通过原点的相交线。当压缩量一定时，最大等效应力随材料厚度的增大而增大，但接触应力的影响因素较多，如压缩量Z、C型环直径d、大径D、材料厚度t及工作温度T等，使得接触应力变化较复杂。如当板厚度为0.30 mm时，最大接触应力随压缩量的增大先增后减，即当压缩量为0.26 mm时，接触应力最大。

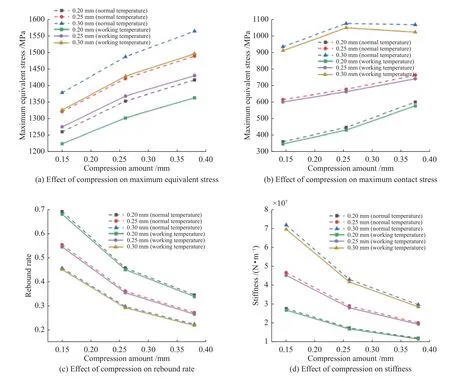
图10 各参量对C型封严环性能的影响Fig.10 Effects of various parameters on the performance of C-type sealing ring

发动机工作时，高温下最大等效应力和最大接触应力小于常温时的最大等效应力和最大接触应力。这主要由于高温下材料的刚度较低，其弹性模量变小；材料厚度一定时，回弹率随着压缩量的增大而减小，当压缩量一定时，材料厚度越大，回弹率越小，这是由于压缩量增大，C环的塑性变形量加大，材料厚度增大，其弹性变形范围变窄，使得C形环较快进入塑性变形阶段。工作温度下的回弹率要小于常温时的回弹率；C环刚度随着压缩量的增大而减小，当压缩量一定时，板材越厚，刚度越大，工作温度时的刚度要小于常温时的刚度。

3 基于响应面法的C型环结构综合优化

应用有限元分析方法得到封严环性能随单个变量变化的规律，但封严环各参数影响关系存在耦合现象，这使得依靠单一参数优化设计难以得到最佳的封严环尺寸。因此，为了考虑各参数耦合作用对封严环性能影响，采用响应面法（RSM）对C型封严环各参数进行优化设计。

RSM是一种结合试验设计和数学建模的优化方法[15-16]。利用合理的试验设计方法并通过试验得到一定数据，采用多元二次回归方程来拟合因素与响应值之间的函数关系，通过对回归方程的分析得到一组最优的参数，从而解决优化问题。

C型封严环的压缩量及板材厚度存在某个最佳组合值，使封严环密封性能最佳，此时封严环回弹率较高，接触应力较大，等效应力较小。因此，选取压缩量、板材厚度2个参数分别作为优化参数A、B。以回弹率、接触应力、等效应力3个参数分别作为优化目标R1、R2、R3。

本次优化设计使用Design-expert软件，利用数值计算得到的数据样本采用多元二次回归方程进行拟合，分别得到响应值R1、R2、R3关于参数A、B的回归方程。并根据拟合出的方程绘制目标参数交互作用的响应面图，以观察各优化目标关于参数A、B的变化趋势。

对回归方程进行分析，并根据封严环的性能要求，期望回弹率更高，泄漏量越小（即接触应力越大）和最大等效应力越小。因此，将回弹率R1及接触应力R2期望目标设为“maximize”，最大等效应力R3期望目标设为“minimize”，并依据这3个性能的重要性，对目标参数（回弹率、接触应力、最大等效应力）的响应值权重分别设为wt1=3，wt2=2，wt3=1。回弹率、接触应力、最大等效应力参数在样本空间中都对应有最大、最小值，分别设为Highi、Lowi，则各响应值期望函数为：

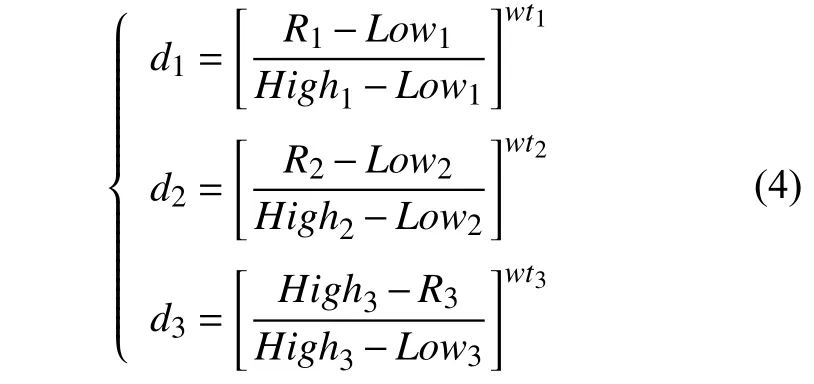
由各响应值的期望函数应用几何平均法可得到优化设计的总体期望函数，在构建整体期望目标函数时，考虑各响应值之间相对权重ri，则总体期望函数构建为：

对于C型环优化中，响应值数量为3个，在本研究中分别取回弹率、接触应力、最大等效应力的期望函数响应值之间的相对权重为r1=4，r2=3，r3=3。则C型环结构参数总体期望函数为：

根据封严环的整体期望函数以及回归方程分析，可得到压缩量和板材厚度2个参数任意组合时的期望值，并绘制出期望值分布图，最终得出期望值最大的组合即为本优化设计最优解。

在工件优化设计中，压缩量范围为0.15～0.38 mm，板材厚度为0.2～0.3 mm，工作温度为900 K，安装尺寸轴向槽深1.8 mm，环直径79.8 mm，环内外侧压差2.7 MPa。经响应面分析得到响应目标拟合回归方程（7），同时绘制目标参数交互作用的响应面图，如图11所示。

图11 目标参数交互作用的响应面图Fig.11 Response surface diagrams of target parameter interaction of sealing ring

由各响应值R1、R2、R3的最大值和最小值代入式（4），可得出d1、d2、d3，再代入式（6）可得到C型环结构总体性能参数期望值的分布（图12）。期望值最大点即为最优结构参数点。由此，可得到该C型环一组最优的参数（表3）。

表3 最优结构参数Table 3 Optimal structural parameters

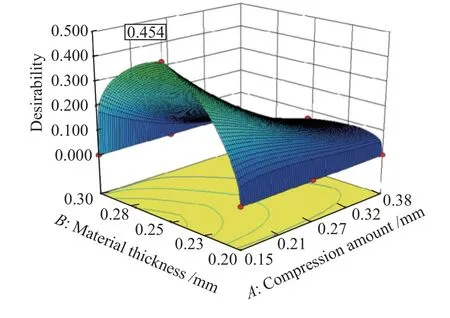
图12 结构参数性能总体期望值分布Fig.12 Overall expected value distribution of structural parameter performance

4 蠕变寿命分析

该C型密封环工作温度为900 K，大大超出了0.3Tm。因此，在恒定载荷和长时间的工作下必然产生蠕变。蠕变现象的产生是温度、时间和应力共同作用的结果。

蠕变本构方程一般模型有时间硬化模型和双曲正弦模型，本研究采用时间硬化模型进行计算，金属封严环应变量恒定，而且变形量不太大，使用时间硬化模型能够满足要求。

根据某型航空发动机大修周期为2000 h，需要保证封严环在寿命周期内不发生失效。因此，对该C型环进行2000 h蠕变分析。图13为C型封严环应力松弛前后的应力分布云图，图14为工作2000 h卸载后的自由高度及应力分布，计算结果见表4。根据C型金属封严环的塑性变形率大于6%，回弹率小于20%，可知该C型环经过优化设计后可以达到蠕变寿命要求。

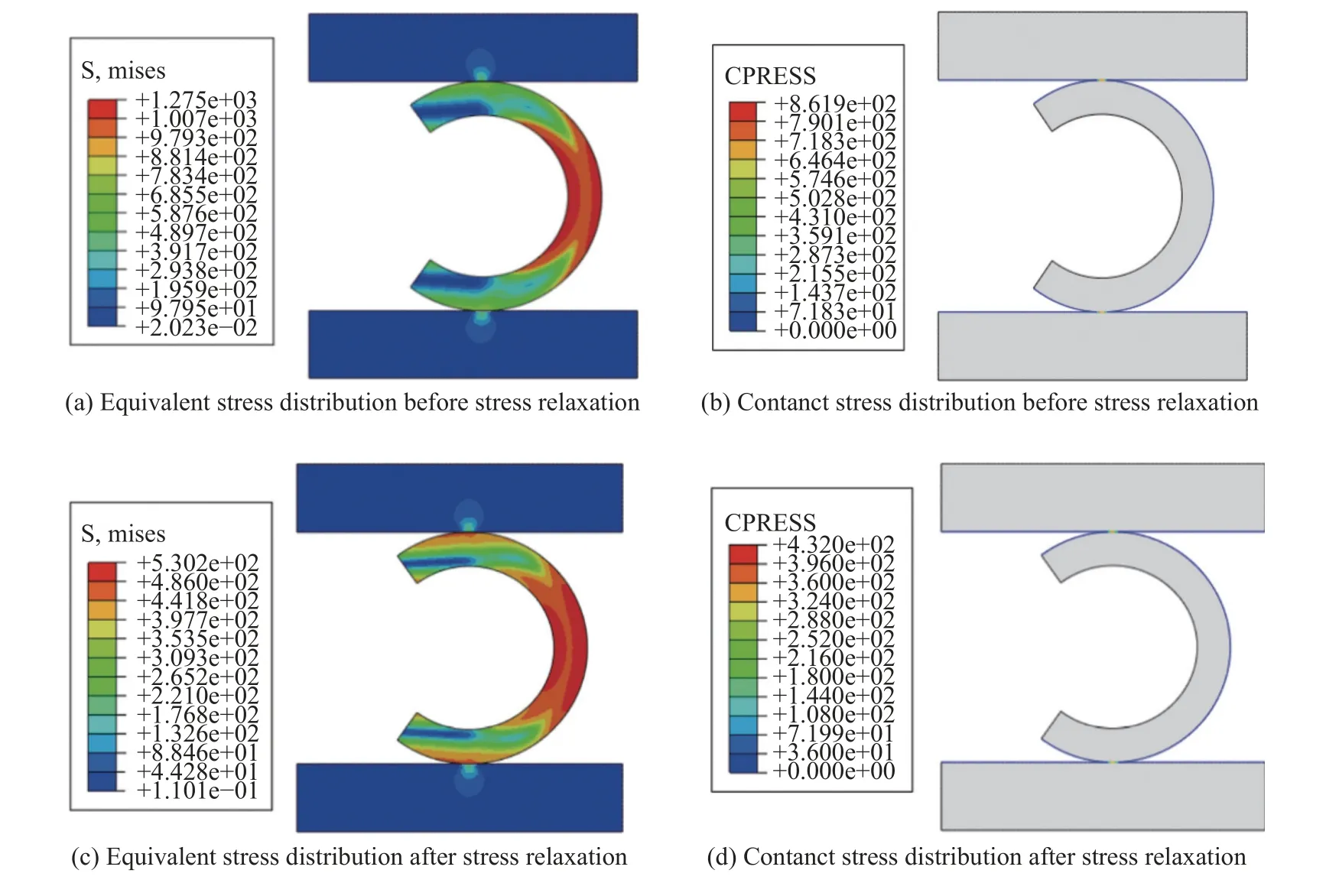
图13 应力松弛前后的应力分布Fig.13 Stress distribution before and after stress relaxation

图14 工作2000 h后卸载的自由高度及应力分布Fig.14 Free height and stress distribution of unloading after working for 2000 hours

表4 C型金属封严环应力松弛前后性能参数Table 4 Performance parameters of C-type metal sealing ring before and after stress relaxation

5 结论

1）C型密封环最大等效应力随压缩量和材料厚度的增大而增大，回弹率随压缩量和材料厚度的增大而减小。

2）C型密封环接触应力变化较为复杂，当板厚度小于0.25 mm时，最大接触应力随压缩量和材料厚度的增大而增大；当板厚度为0.30 mm时，最大接触应力随压缩量的增大先增后减。

3）以压缩量、板材厚度为自变量，回弹率、接触应力、最大等效应力为响应值，采用响应面法对C型密封环结构进行优化设计，经蠕变疲劳寿命分析，表明优化的结构尺寸满足疲劳寿命的要求。