广义可加模型的拟最优样本选择方法

秦 磊,叶玲珑,谢邦昌

(1.对外经济贸易大学 统计学院,北京 100029;2.厦门大学 公共事务学院,福建 厦门 361005;3.台湾辅仁大学 管理学院,台湾 242062)

一、引言

大数据开启了一个时代的转型,带给人们的是信息的丰富积淀和思维的巨大变革,同时也使得数据的建模和预测面临着新的困难和挑战。随着数据搜集和储存能力不断提升,数据量大成为大数据的首要特征,即便是简单的计算公式,也有可能伴随着巨大的计算成本。为此,如何筛选有效的信息并且在有限的计算条件下还原大数据中的统计特征就成为当下值得深入思考的问题。

为了高效便捷地探索大数据统计特征,一个有效的做法就是抽样,即选取具有代表性的抽样样本来代替全体从而刻画变量之间的关系并进行有效预测。文献中给出的抽样方式通常有两种,一种是概率抽样也叫随机抽样,另一种是非概率抽样。而在概率抽样中最常用的是等概率抽样(均匀抽样),原始数据的所有样本点以相同的概率进入新样本中。但该抽样方法有明显的缺陷,当样本为不均衡样本时该方法往往表现很差。受到这个问题的启发,很多统计学家基于数据本身的特殊结构提出了大规模数据的非均匀抽样方法,用于提升小样本的估计精度。一个经典的做法就是基于观测矩阵的Leverage分数对观测矩阵的行或者列做不等概率抽样之后,再进行各种参数估计或者矩阵计算,这样Leverage分数较高的数据更有可能进入新的样本,文献主要包含:最小二乘近似的研究,见Drineas等[1-2];最小一乘近似的研究,见Meng和Mahoney[3];低秩矩阵近似的研究,见Mahoney和Drineas[4]。这方面较为全面的总结和回顾可以参照Mahoney,另外Ma等给出了Leverage重要性抽样的统计理论,并以大量的数据分析证实该方法的可行性及有效性[5-6]。然而Leverage重要性抽样也具有一些缺陷,例如Leverage分数并不是一个直接影响估计精度的指标,不等概率抽样也可能令某些重要的样本漏选,而且抽取样本得到的估计不具有唯一性。

样本选取的另一种方式是确定性抽样,也称作非概率抽样,其本质思想是寻找一个直接影响估计精度的条件和准则,然后按照这种准则对样本点排序,依次选择重要的样本点。相比于概率抽样,这种方法的难点在于抽样准则的寻找,但是这种方法不会因随机筛选而漏掉某些具有代表性的样本点,并且由于抽样样本的确定性,模型的估计结果也相对唯一。确定性抽样的文献相对较少,这源于保证抽样估计精度的准则较难寻找,一个有趣的做法是Shin和Xiu[7]对于线性回归的研究,作者希望通过选择一个小样本来近似全样本的最小二乘估计结果,他们对小样本估计量和全样本估计量的差距进行理论分析后找出了最具代表性的抽样样本应该满足的条件,给出了一种样本选择的标准,数值分析的结果显示了这种做法要优于常见的概率抽样方法。

本文综合借鉴了随机抽样与确定性抽样的思想,考虑了更为复杂的广义可加模型的估计问题[8]。选取的原因在于,该模型是重要的半参数模型,可以拟合复杂的数据结构,避免高维协变量下维数灾难的影响,而且估计结果更具有解释性,在实证分析中有着广泛的应用。另外,对于大规模数据的参数估计问题,很多学者也都从广义可加模型入手,例如Wood等以及许亦频和倪苹对此的总结[9-10]。本文考虑的这类模型可以写为:

(1)

其中,Y是服从指数分布的响应变量,X是已知的自变量向量,g{·}是连接函数,fj是一个或者多个自变量形成的未知光滑函数,βj是函数中包含的未知参数。式(1)包含常见的广义可加模型、广义部分线性模型、广义变系数模型等等。本文的主要贡献在于,一方面将确定性抽样的理论从线性模型的情形扩展到广义可加模型上,这种方法不仅包含了部分线性可加模型,也同样适用于变系数模型和部分线性变系数模型的估计,另一方面由于广义可加模型在估计过程中需要用到惩罚估计,因此确定性抽样的理论也可以扩展到岭回归等惩罚估计方法。

本文通过高斯连接函数下可加模型的估计过程给出抽样样本应该满足的正交性条件,并提出基于此条件的最优样本选择方法,将结果推广到复杂连接函数和广义变系数模型,并补充了计算过程中的一些细节。然后,分别在模拟数据和实际数据上,比较了本文提出的方法和概率抽样方法的估计精度和预测精度。

二、高斯连接函数下的样本选择条件和拟最优样本选择算法

(一)样本选择条件

考虑高斯连接函数g{μ}=μ下广义可加模型的样本选择条件,假设Y=(Y1,Y2,…,YN)T是N×1维的因变量,X=(X1,X2,…,XN)T是N×p维的观测矩阵,其中Xi=(Xi,1,Xi,2,…,Xi,p)T是第i个个体p个特征的观测值,可加模型可以写为:

Yi=f1(Xi,1)+f1(Xi,2)+…+fp(Xi,p)+εi

(2)

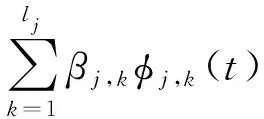
(3)

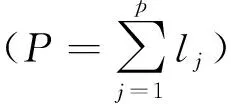
Y=Φβ+ε

(4)

其中β=(β1,1,…,β1,l1,…,βp,1,…,βp,lp)T。由于基函数会增加解释变量的个数,为此一般会采用类似岭回归的方式去做惩罚估计,

(5)

其中,βTΩβ是二次惩罚函数,Ω是预先设定的惩罚结构,设定方式见第3节。式(5)可以通过求导得到显示解:

(6)

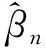
(7)

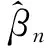
(8)

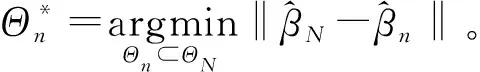
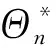
(9)

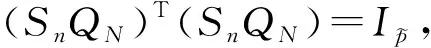
(二)拟最优样本选择算法

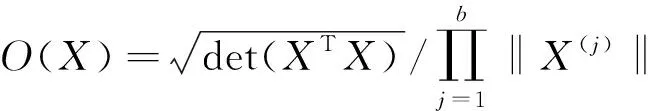
(10)

特别地,如果ΦN本身就是正交矩阵,那么无需对ΦN进行Skinny QR分解,这个问题可以直接写为:

(11)

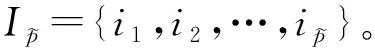
(12)

其中QIk表示矩阵QN对应于Ik的所有行,数据集ΘN的行标号集合为IN。第3步:重复执行第2步,直到选出n个样本为止。

值得注意的是,上述算法采用了贪婪的策略,依次选入了最大化正交指标的样本,其结果可能只是局部最优的,这种方式类似于聚类算法中的K均值聚类。另外,由于前P个样本的选取具有一定随机性,所以我们最终得到的样本子集会略有不同,但是由于P相对于n比较小,因此并不影响参数估计的结果。出于以上两点,本文的样本选择算法给出的是一个拟最优的结果。

三、算法扩展及计算细节

(一)复杂连接函数下的算法扩展

(13)

结合前述分析不难看出,该模型的样本选择问题可以被定义为如下优化函数:

(14)

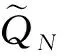
(二)广义变系数模型下的算法扩展

提出的样本选择方法也适用于广义变系数模型[11],这里以高斯连接函数为例进行简要说明,其模型表示为:

Yi=β1(Ri)Xi,1+β1(Ri)Xi,2+…+βp(Ri)Xi,p+εi

(15)

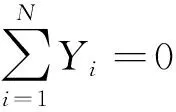
(16)

其矩阵形式写成:

Y=Ψγ+ε

(17)

Ψ的第i行Ψi=[φ1,1(Ri)Xi,1,…,φ1,l1(Ri)Xi,1,…,φp,1(Ri)Xi,p,…,φp,lp(Ri)Xi,p]T,系数向量γ=(γ1,1,…,γ1,l1,…,γp,1,…,γp,lp)T。由于式(20)含有较多的基函数变量,一般也会采用类似岭回归的方式去估计:

(18)

式(21)的显示解为:

(19)

(三)计算中的一些细节

1.基函数的选择

(20)

其中结点ξj1、ξj2和ξj3分别为第j个变量的25%、50%和75%分位数。

2.惩罚函数中Ω的选择

由于估计过程中基函数展开引入了较多的解释变量,会造成估计量的方差增加以及预测精度的下降,因此要对估计参数施加一定的惩罚约束,表示为式(4)中的βTΩβ,其中Ω是惩罚的权重矩阵,Ω中的元素越大,惩罚力度将越大,β的估计量将越接近于0,在文献中Ω有很多选择方式,本文令Ω为对角阵,对于第j个变量而言,βjk中k=1时,Ω对角阵相应的元素为0,k≠1时,Ω对角阵相应的元素为1,表示为:

Ω=diag{0,1,1,1,1,1,…,0,1,1,1,1,1}

(21)

这样就以岭回归的方式对基函数中的二次和三次项进行约束,虽然估计量增加了一些偏差,但是系数的约束换来了方差的下降,而使得估计量的预测误差下降。

3.调整参数λ的选择

在可加模型的收缩估计中,调整参数λ决定了惩罚力度。当λ=0时,参数估计相当于无约束的最小二乘法,当λ→∞时,参数估计都趋向于0,λ越大参数估计就越靠近于0。选择λ通常使用的准则有AIC、BIC、CV和GCV准则等[12-14],高斯连接函数下,本文选择了BIC准则用于选取调整参数λ,表示为式(17),其中A(λ)=Φ(ΦTΦ+λΩ)-1ΦT。BIC准则的左右两个部分体现了样本内的预测误差和复杂程度,两者的变化具有相反的方向,而λ将选取一个折中的状态:

BIC(λ)=nlog[(Y-AY)T(Y-AY)]+log(n)trace(A)

(22)

四、数据分析

(一)模拟数据分析

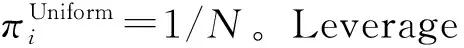
参考已有文献,本文构造了三种模型用于产生可加结构的数据集,其中模型1来源于Koenker,模型2来源于Huang等,模型3来源于Xue等[15-17]。每种模型中的自变量都产生于[0,1]上的均匀分布,扰动项ε～N(0,0.22)。

2017年大连市三次产业结构比例为6.4∶41.5∶52.1，第三产业占比超过一半以上，形成了以服务经济为主导产业结构，服务业成为稳增长的 “压舱石”。工业结构不断优化，数控机床、轨道交通、核电装备、集成电路、储能装备等领域推出一批新产品、新技术，2017年全市规模以上高技术产业增加值增长50.8%，战略性新兴产业增加值增长16.5%。 “互联网+”迅猛发展，新技术、新产业、新业态、新模式快速成长，2017年规模以上软件和信息服务业实现营业收入增长19.7%。投资结构进一步优化，高技术产业投资增长94.1%，民间投资增长22.4%，服务业投资占比达62.4%。

模型2:Y=5X1+4sin(2πX2)/(2-sin(2πX2))+ε

模型3:Y=2X1+8(X2-0.5)3+sin(2πX3)+ε

图1～3分别给出了三种模拟数据下的估计结果对比,每张图左侧表示样本内的参数估计误差,右侧表示样本外的预测误差。从三个模拟数据的结果上看,简单随机抽样下的结果是最差的,其次是Leverage抽样,而拟最优样本选择是最优的,其误差曲线均处于最低的位置,说明该方法选出的样本具有更好的代表性,有利于参数估计和数据预测。虽然Leverage抽样和拟最优选择方法都是以重要性来选择样本的,但是前者的重要性度量建立在Leverage值上,和估计以及预测没有很大关系,而后者建立在正交性条件上,是用来尽量减少估计误差的,因此拟最优样本选择具有相对优势。另外,从图形的细节上可以发现一些事实:拟最优样本选择对参数估计的提升要明显高于预测误差的提升,因为本文在寻求样本选取准则的时候就是从参数估计误差来入手的,因此该准则将更偏向于参数估计的提升;在样本量增大的情况下,三种方法的估计和预测误差都在下降;可加模型的样条估计中常用的基函数都不是正交的,因此无法使用式(10)进行计算,如果可以找到正交的基函数,那么式(10)将是一个计算负担较小的准则。

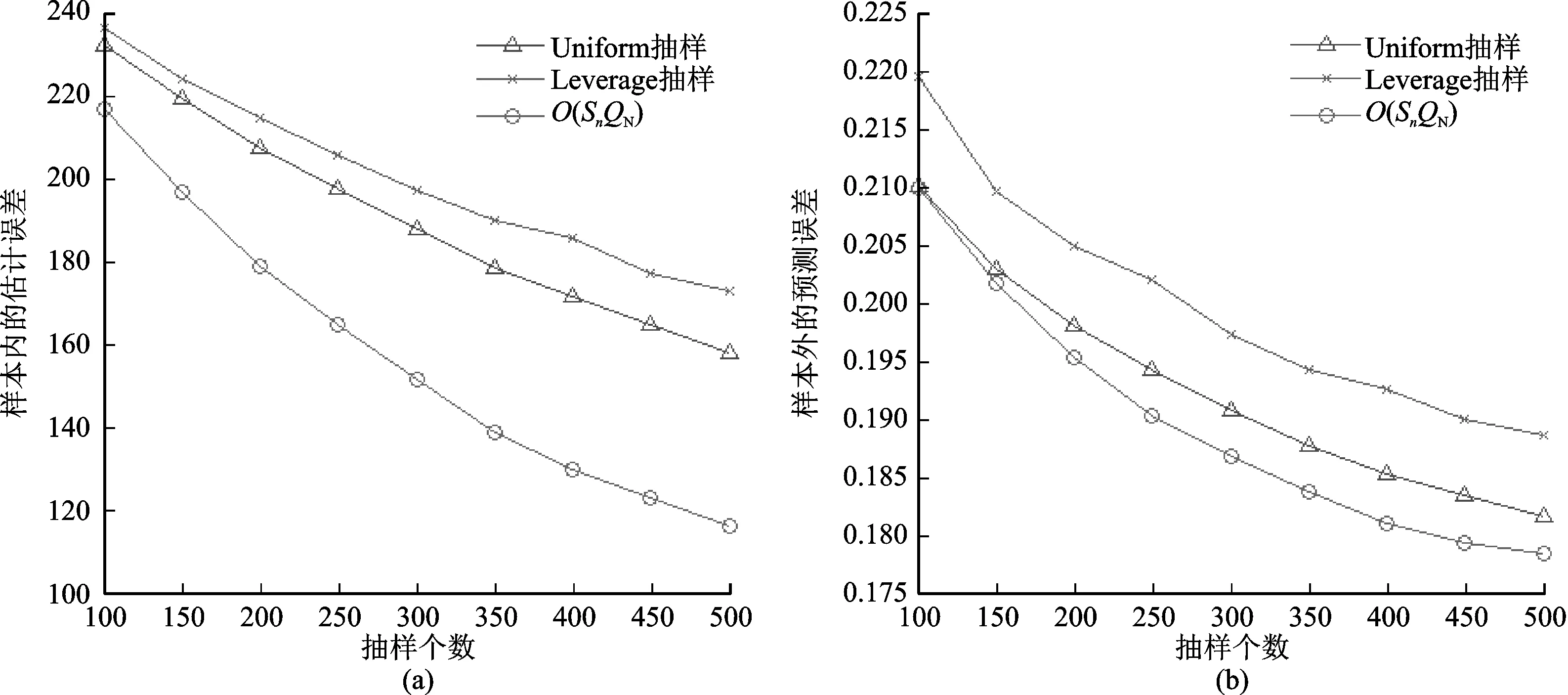
图1 模拟数据1的估计结果对比

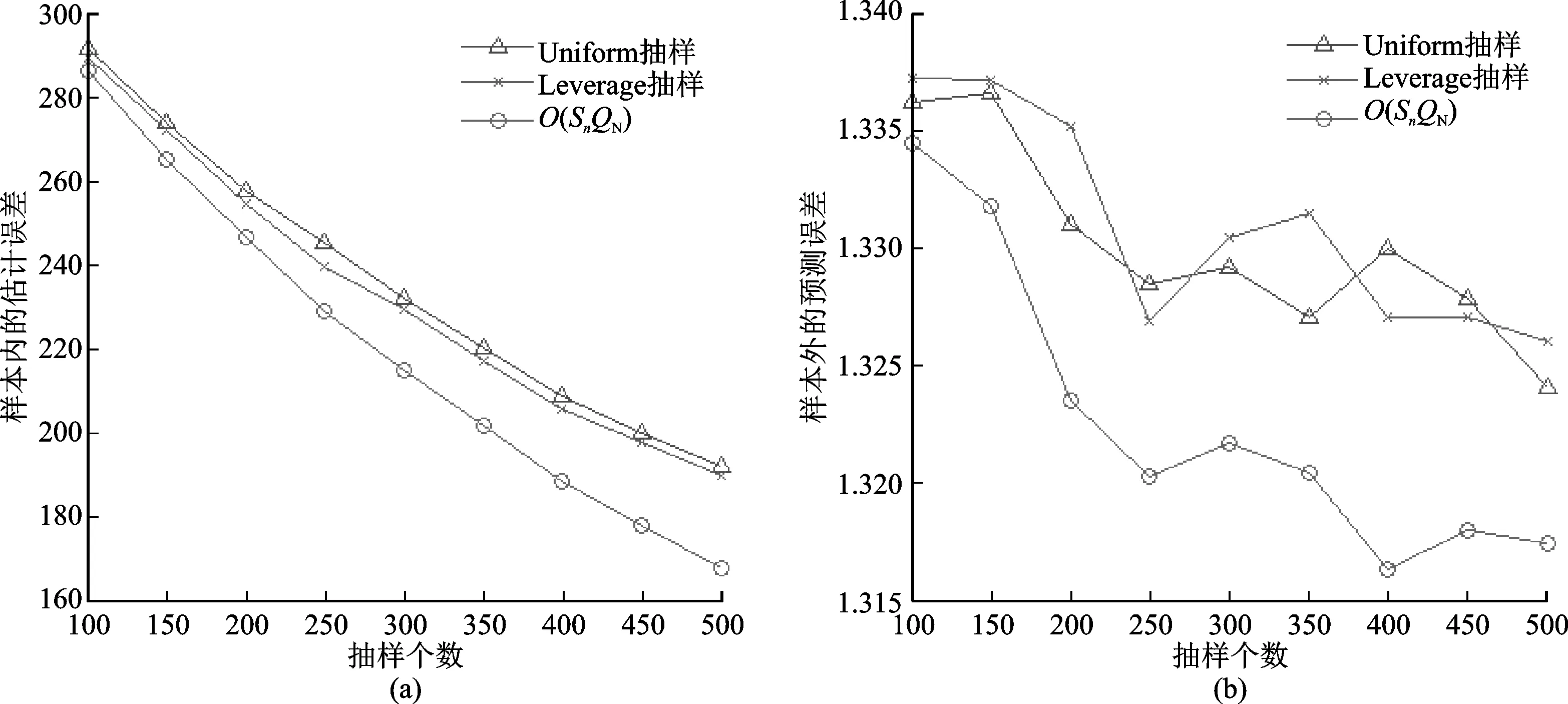
图2 模拟数据2的估计结果对比

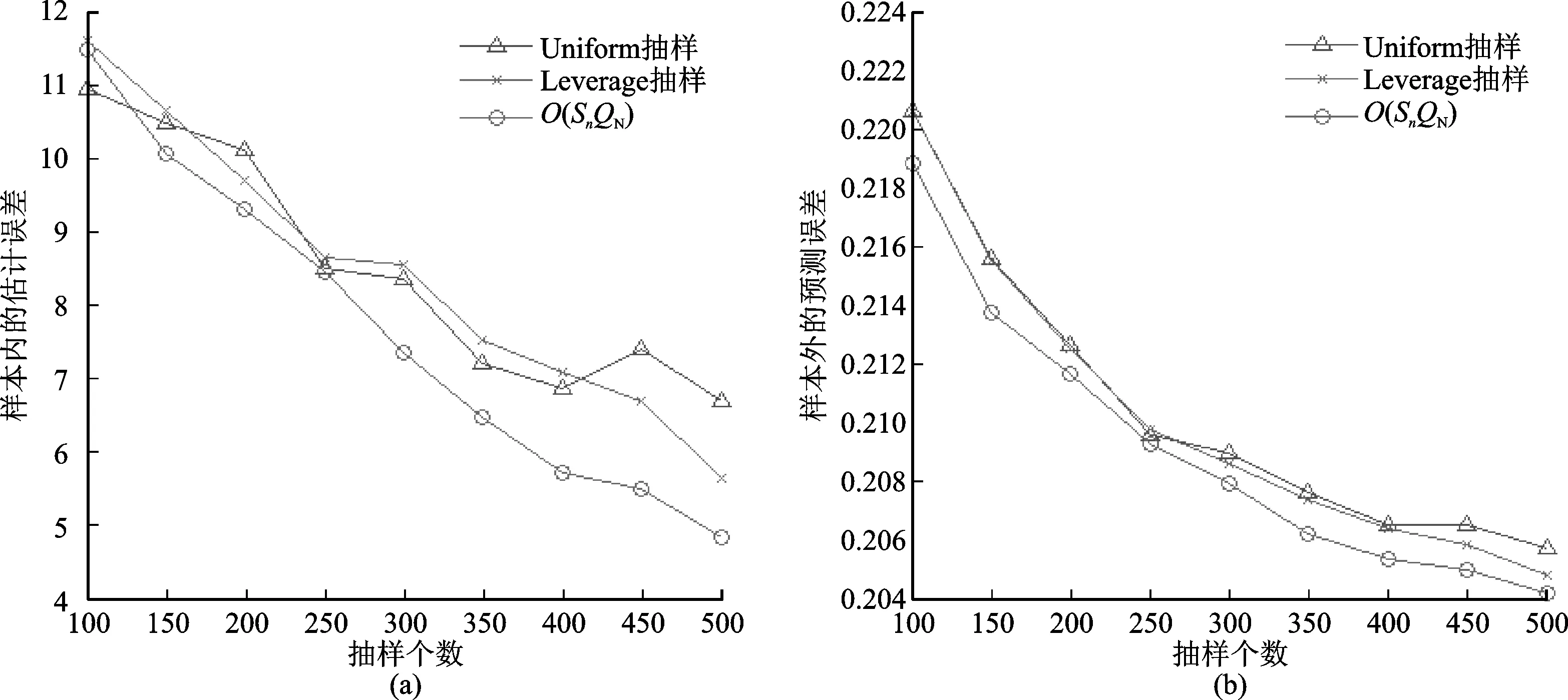
图3 模拟数据3的估计结果对比

(二)实际数据分析

本文提出的方法可以用来分析政府统计和经济统计中产生的微观大数据。以UCI数据库的Bike Sharing数据集为例[18],对比了可加模型结合拟最优样本选择、简单随机抽样和Leverage抽样在实际数据中的估计效果。

Bike Sharing数据集来源于美国某城市公共自行车共享系统,该系统中用户注册、租借和归还自行车都是自动的。用户可以从一个地方租一辆自行车,然后在另一个地方归还,整个行程的起点、终点、时间都会被详细地记录下来。自行车共享系统的运行对于整个城市的交通、环境和健康问题都做出了巨大的贡献,因此运行中产生的数据受到了越来越多学者的关注。该数据集以小时为单位记录了车辆租借次数、当时的日期和天气状况,时间跨度为2011—2012年,共有17 389条数据,目的是探索租借次数和环境变量之间的关系。

本文租借次数作为响应变量Y,温度、体感温度、湿度和风速作为预测变量X,在1～9 000条数据形成的训练集上结合三种抽样方式进行可加模型的估计,在9 001～17 389条数据形成的测试集上进行预测,参数估计误差和预测误差随抽样次数的变化呈现在图4中。可以看出,对于参数估计误差,拟最优样本选择下通常是三种方法中最低的;对于样本外的预测误差,抽样个数小于350的情况下拟最优样本选择和随机抽样有相近的表现,但是在大于350以后拟最优样本选择是三种方法中最低的。因此从整体上来看,本文提出的方法在实际数据上具有较好的效果。

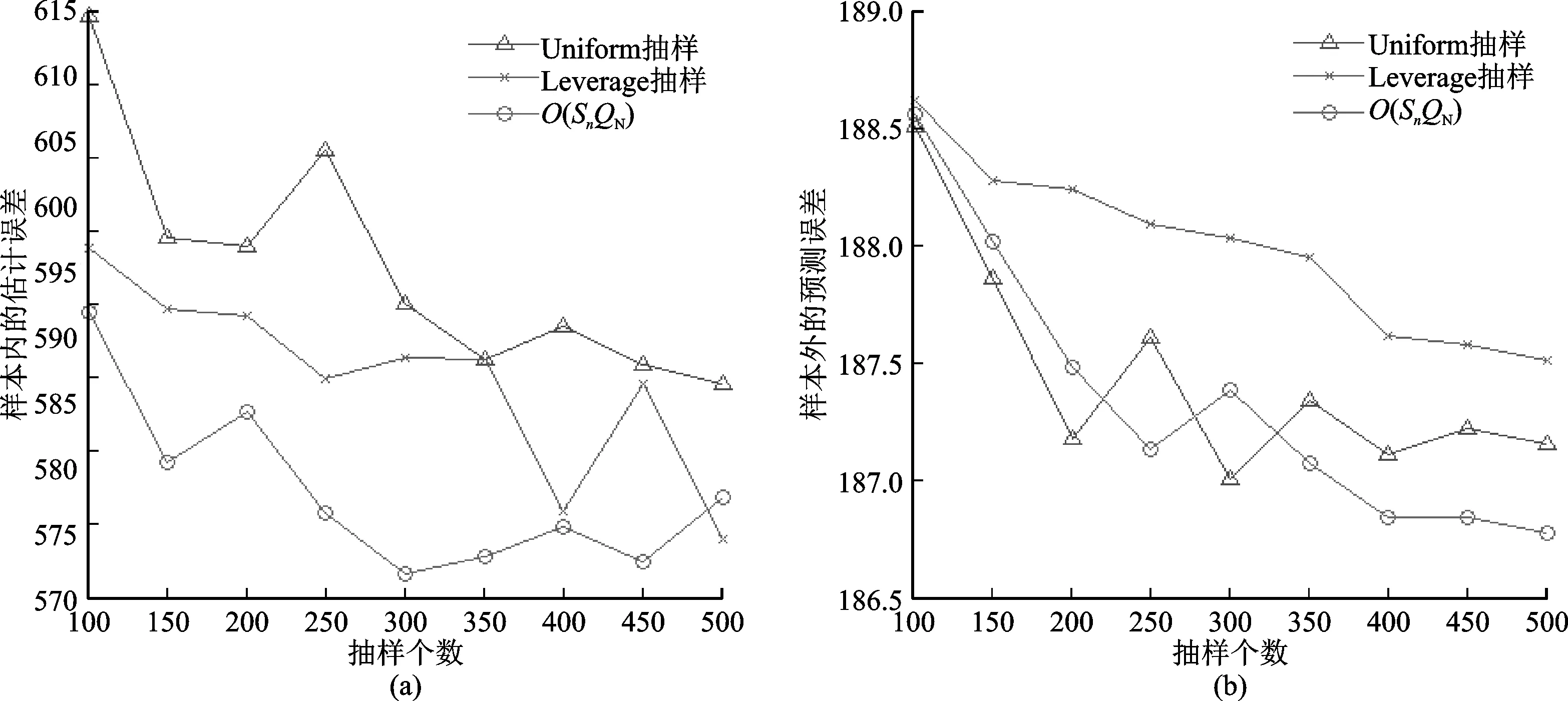
图4 Biking Sharing数据集的估计结果对比

五、结论和未来的研究方向

面对海量数据,如何选取一个合适的样本子集去精准还原大数据中的统计特征是值得深入思考的问题。本文主要研究了广义可加模型的确定性抽样方法,通过比较全样本和抽样样本估计结果之间的差距,发现样本选择应该满足正交条件。在给定的正交性指标下,进一步给出了一种贪婪算法用于寻找最大化正交性指标的局部最优解。由于初始值的随机性,因此本文的样本选择算法给出的是一个拟最优的结果,大量的模拟数据和实际数据集也证实了该方法的可行性、科学性及有效性。

本文讨论了大数据下广义可加模型和广义变系数模型的确定性抽样方法。在未来的研究过程中,可以进一步研究以下问题:(1)在目前的样本选择条件下,是否存在一个更优的正交性指标,用于提升样本选择的质量。由于目前的正交性指标需要以P个样本为前提,导致提出的算法获得了拟最优的结果。如果正交性指标能够以更少的样本为基础,那么样本会更加接近于全局最优选择的结果。(2)是否存在新的样本选择条件,使得估计和预测具有更高的精确程度。本文的样本选择条件是通过比较全样本和抽样样本的估计结果而给出的,原则上样本选择条件会随着估计方法、损失函数或抽样设计[19]而变化,进而影响估计和预测的结果,因此具有最优预测性能的样本选择条件是个值得研究的问题。