低压线路的阻抗计算及拓扑识别方法研究
严永辉,李新家,周瑞雪,刘飞,吴甲
(江苏方天电力技术有限公司, 技术部, 江苏, 南京 211102)
0 引言
电能传输线路分为低压配电线路和高压配电线路,目前人们对高压配电线路和输电线路做了大量研究[1],但低压配电线路由于网络结构复杂多变,无法掌握配电线路的工作状态[2],且低压配电线路的配电设备和配电线路在长期使用过程中容易老化线路阻抗,进而对故障定位、线损计算、短路电流计算、故障分析的最终结果产生影响。
WARTENBERG D等[3]在故障侦测方面开展低压用电网的阻抗实施监测,在故障定位、排查隐患等方面利用电网阻抗进行计算,对研究低压线路阻抗具有重要作用。董清等[4]通过双端测量方法以单回不换位线路为例对电路阻抗进行计算,该方法没有对低压线路首端和末端的电流、电压数据进行融合处理。梁祖权等[5]在电路首末两端安装电能质量分析仪分析电压通道和电流通道,获得电流相量值和电压相量值,对线路阻抗进行计算,该方法没有融合电能质量分析仪获取的数据,无法在短时间内根据线路阻抗准确地实现拓扑识别,存在拓扑识别精准度低、拓扑识别效率低的问题。为了解决上述方法中存在的问题,本文提出利用测量装置获得多源数据,从而实现高效准确的低压线路阻抗及拓扑识别方法。
1 低压线路的阻抗计算及拓扑识别方法
本文为减小阻抗值的均方根误差、提升拓扑识别精准度和效率,利用低压线路监测终端等测量装置在配电台区获取无功功率、电压、有功功率和电流等多源数据,结合配电台区用户智能电表与线路之间的连接情况可以准确推算出各条线路在时间序列内的阻抗值,在计算低压线路阻抗后设计拓扑识别方法[6]。
1.1 低压线路阻抗计算方法
以下游用户智能电表节点1与边缘器二侧出口处的节点a为例(如图1所示),计算低压线路的阻抗[6]。
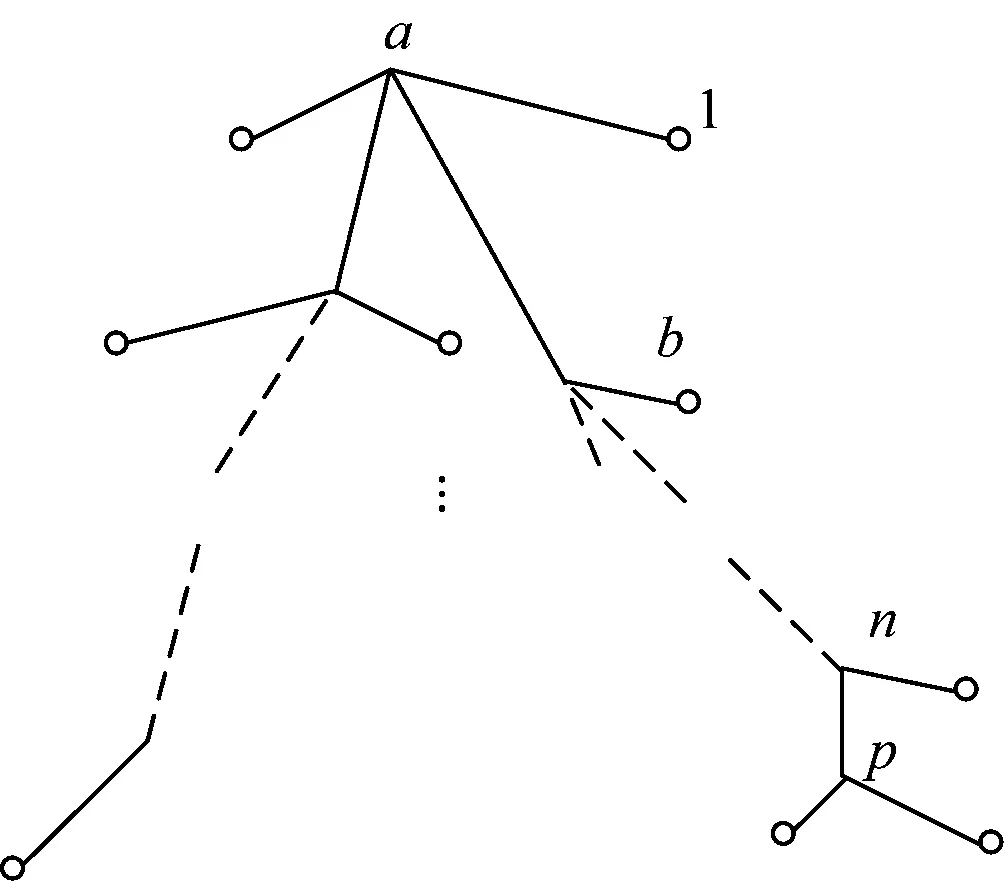
图1 低压配电网台区拓扑图
设Za-1代表节点1与节点a之间存在的线路阻抗,则:
Za-1=R1+jX1
(1)
式中,X1代表线路对应的电抗,R1代表线路对应的电阻,j代表线路数量。
上游节点a与下游节点1的线路中在t时刻根据欧姆定律获得式(2):
(2)
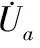
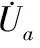
(3)
(4)
式中,P1代表有功功率,Q1代表无功功率。
通过配电台区SM或CTU在t时刻提供的测量数据计算节点1处对应的无功功率Q1、电压U1、有功功率P1和电流I1,则:
P1=U1I1cosφ1
(5)
Q1=U1I1sinφ1
(6)
上游节点a对应的电压Ua可通过线路首末两端的电压关系计算得到:
(7)
通过联立方程组获得支路对应的阻抗值[7],同理推导点b的电压为

(8)

(9)
式中,m代表下游用户智能电表和支路在节点b中的总数。
节点a电压矩阵的行向量元素选取配电变压器二次节点a的所有电压值Ua为
Ua=f(Z1,Z2,Z3,…)=f(R1,R2,R3…,X1,X2,X3…)
(10)
获得含有各条线路未知阻抗分量在不同时刻下的电压矩阵为
(11)
设(Uat)MSE代表电压值在电压矩阵中的均方误差:
(12)
式中,(Uat)measured代表上游节点a在t时刻对应的电压值。
不考虑用户智能电表受测量设备影响产生的测量误差[8],即(Uat)MSE=0。
1.2 拓扑识别
构成特征向量集合{u1(t),u2(t),…,un(t)},其中t=0,Δt,2Δt,…,MΔt,M代表最大采样点数,Δt代表采样间隔。
节点顶点为xi,其中i=1,2,…,n,设S(i,j)代表顶点xi与顶点xj之间的相似程度,由xj构成邻接矩阵W(i,j),其中0≤W(i,j)=W(j,i),W(i,i)=1,i,j=1,2,…,n。
利用相似度矩阵W(i,j)进行度量距离[9],采用ε邻接法构建邻接矩阵W(i,j),设置距离阈值ε,通过欧式距离对xi、xj之间距离进行度量,即相似矩阵中存在的元素sij:
(13)
确定邻近矩阵中元素对应的值wij:
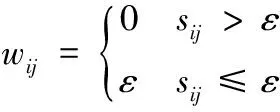
(14)
构建配电网等效网络G(V,E,W),获得k个互相不连接的子图,用A1,A2,…,Ak描述每个子图点对应的集合,且符合Ai∩Aj=Ø,A1∪A2∪…∪Ak=V,
用拉普拉斯矩阵特征值聚类问题代替低压线路拓扑识别问题[10],具体流程如图2所示。
(1) 构建邻接矩阵w:
(15)
其中,σ代表核参数。
(3) 对拉普拉斯矩阵L=D-w进行计算。
(4) 对计算得到的拉普拉斯矩阵进行归一化处理,获得矩阵L’。
(5) 设λ代表矩阵L’对应的特征值,计算得到:
L′f=λDf
(16)
其中,f代表矩阵F中存在的元素。
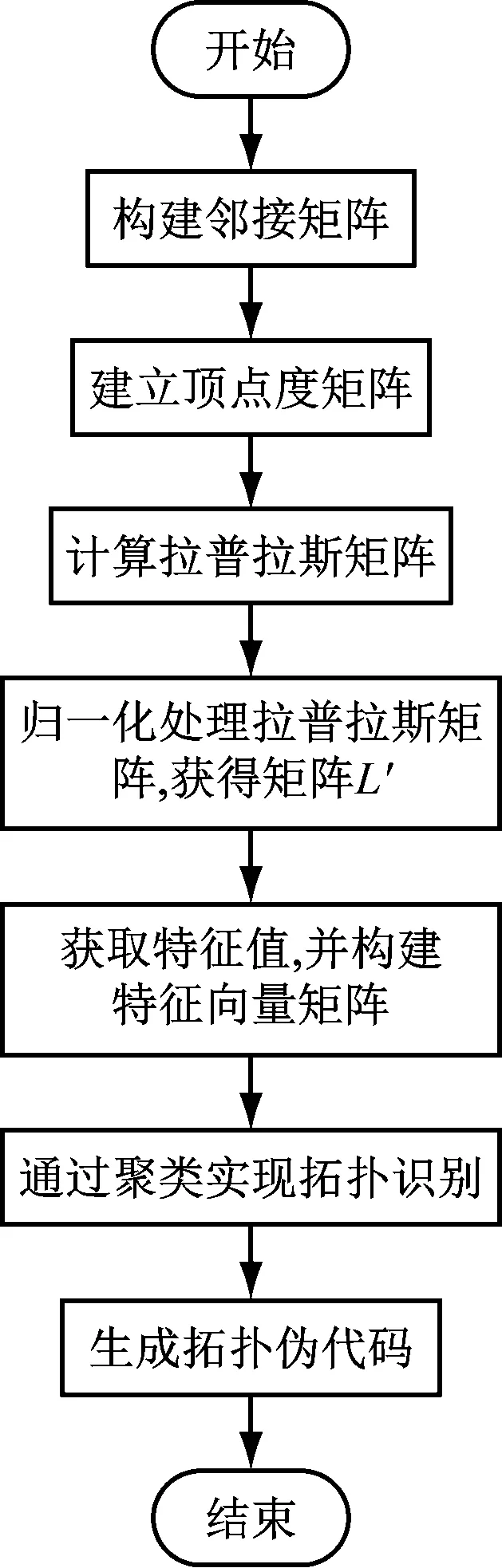
图2 拓扑识别流程图
(6) 对前k个特征值的特征向量进行计算,建立矩阵F=(f1,f2,…,fk)。
(7) 矩阵F中存在的每一行都可以作为k维的样本,通过聚类方法获得馈线与配电变压器值之间的对应关系,完成拓扑识别,识别后对特征值进行排序,生成拓扑伪代码:
Void TopologicalSort(GraphW){
InitStack(u);
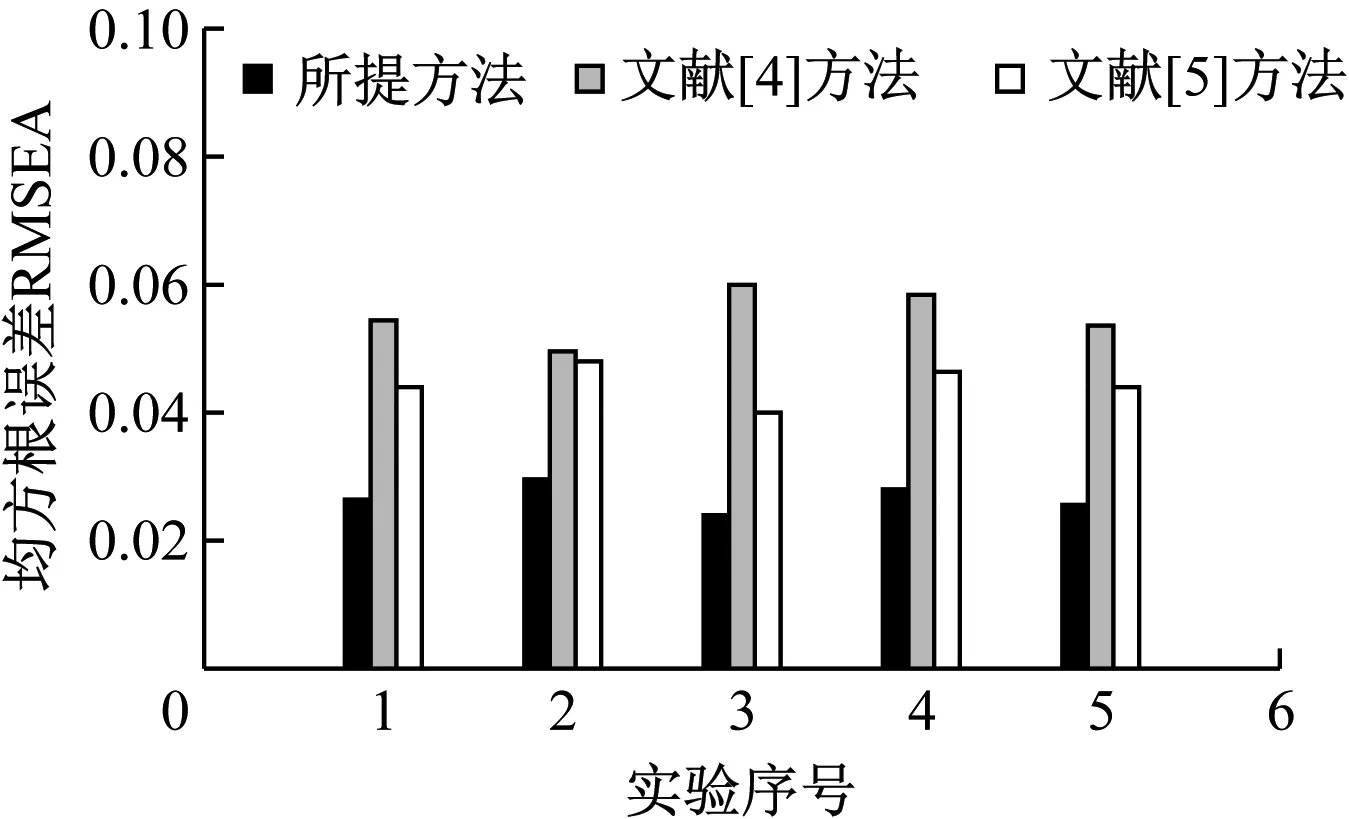
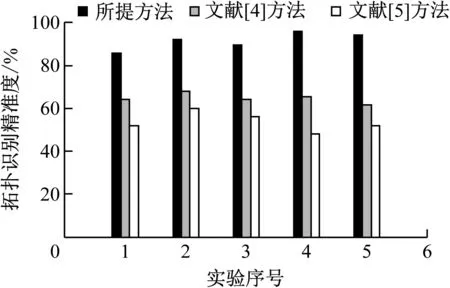
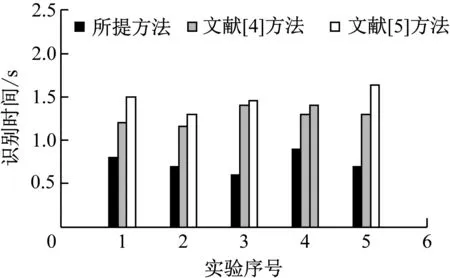
for(i= 0;i if(indegrdd[i]==0) Push(u,i); } Int count =0; While(!Empty(u)){ Pop(u,i); print[count++] =i; For(λ=W.vertices[i].firstarc;λ;λ=λ->nextarc){ F =λ->adjvex; if(!(--indegree[F])) Push(u,F); if(count Return false; else Return true; }。 为验证低压线路的阻抗计算及拓扑识别方法的有效性,以某地区低压配电网为研究对象,分别采用本文所提方法、文献[4]方法和文献[5]方法对低压线路的阻抗进行计算。为保证实验的客观性,实验次数设置为5次,对比不同方法的计算结果的均方根误差RMSEA,测试结果如图3所示。 图3 均方根误差测试结果 由图3可知,文献[4]方法和文献[5]方法获得的结果误差较大,所提方法计算低压线路的阻抗时获得的均方根误差均在0.04以下,均方根误差小于0.04在可接受范围内,造成的影响较小,这是由于本文方法在拓扑识别前利用低压线路监测终端等测量装置在配电台区获取无功功率、电压、有功功率和电流等多源数据,计算各条线路在时间序列内的阻抗值,降低了均方根误差。 将拓扑识别精准度作为测试指标对所提方法、文献[4]方法和文献[5]方法进行测试,拓扑识别精准度测试结果如图4所示。 图4 拓扑识别精准度测试结果 由图4可知,所提方法在多次实验中的拓扑识别精准度均高于文献[4]方法和文献[5]方法,因为所提方法对电网营配数据进行了融合处理,根据融合后的数据对低压线路的阻抗进行计算,并将其作为特征值实现拓扑识别,提高了所提方法的拓扑识别精准度。 采用所提方法、文献[4]方法和文献[5]方法进行测试,通过识别时间验证不同方法的拓扑识别效率,测试结果如图5所示。 图5 识别时间测试结果 由图5可知,所提方法识别线路拓扑结构所用的时间最低,证明所提方法可在较短的时间内计算低压线路的阻抗,实现拓扑识别,缩短了识别所用的时间,提高了所提方法的识别效率。 运用传统方法对低压线路阻抗拓扑结构时存在阻抗计算结果均方根误差大、拓扑识别精度低和识别效率低的问题。本文为解决上述问题,提出低压线路的阻抗计算及拓扑识别方法,在低压线路阻抗计算过程中对数据进行融合,融合电网营配数据可以为配电网的运维提供决策支持,根据低压线路的阻抗值实现拓扑识别,解决了传统方法中存在的问题,为配电网的稳定运行提供了保障。2 实验及分析
3 总结

