基于迁移学习的网络身份双向认证技术

马海瑛

(吉林师范大学分院, 现代教育技术中心， 吉林， 四平 136000)

0 引言

在网络环境中的信息系统应用过程中，身份认证是一个极为重要的步骤，在没有确定试图访问受限资源的主体身份前，企业网络系统不能将访问权限授予该用户。这样做更有利于系统的安全管理审计。

现阶段关于身份认证的技术较多，文献[1]提出一种基于格理论的装备保障信息网络快速身份认证方案。该方法针对传统身份认证方案无法抵抗量子计算机攻击的问题，引入双峰高斯抽样技术和本格抽样算法实现量子环境下的安全身份认证。通过实验得出该方案达到了身份不可伪造性的目标，但是该方案的认证效率相对较低，不具备同步性。文献[2]提出一种更安全的匿名三因子多服务器身份认证协议研究。通过椭圆曲线密码机制保证了在认证阶段系统的安全性，利用与同类认证对比分析表明该方法能够实现匿名性，且安全性较高。但是算法本身较为复杂，操作性较差。

本文针对上述问题，以迁移学习方法为理论基础，提出了一种网络身份双向认证技术。为确保认证的安全性，通过椭圆曲线加密机制和基点的选择获得公钥和私钥数列，实现网络服务器和用户身份间的双向认证。最后通过仿真实验证明所提方法的同步性与抗攻击性较好，能够基本保障网络用户的身份安全。

1 网络身份双向认证技术

1.1 迁移学习法的弱相似性训练

迁移学习算法作为一种将已知模型参数放置到新模型、帮助模型训练的方法[3]，能够有效对网络中已知的用户数据及身份数据进行重新模拟训练，提高认证效率和安全性[4]。

首先给定源领域数据集和目标领域数据集分别为S、T，二者的样本空间相同。假设x表示特征量，y表示类标号，记作T={(xi,yi)|i=1,2,…,m}，S={(xi,yi)|j=m+1,m+2,…,m+n}，其中m和n分别表示两个数据集的样本数量。假设源领域的样本变量分布服从PS，记作(XS,YS)～PS(X,Y)。目标领域样本变量分布服从PT，将其记作(XT,YT)～PT(X,Y)。两个领域对应的条件分布和边缘分布分别记作PS(X),PS(Y|X)和PT(Y|X),PT(Y|X)。在迁移学习的过程中，PS和PT相互关联但是不完全相同。

给定一个源域Ds、一个学习任务Ts和一个目标域Dt、学习任务Tt，迁移学习的中心思想即为从Ds和中学习从而获得相关知识，运用至Dt中，从而完成Tt的Ts学习任务。设域D={X,P(X)}，X=x1,x2,…,xn，P(X)表示与特征空间X对应的边际概率分布。任务T中同时含有条件概率分布P(M|X)和标签类空间M，通常情况下，P(M|X)是通过特征—标签对xi∈X，Mi∈M所组成的训练数据中获得。迁移学习的主要目的为在Ds≠Dt，Ts≠Tt的前提下，从Ds和Ts中学习获得信息，求得目标域Dt中条件概率的分布P(Mt|Xt)。图1给出了迁移学习的基本思想。

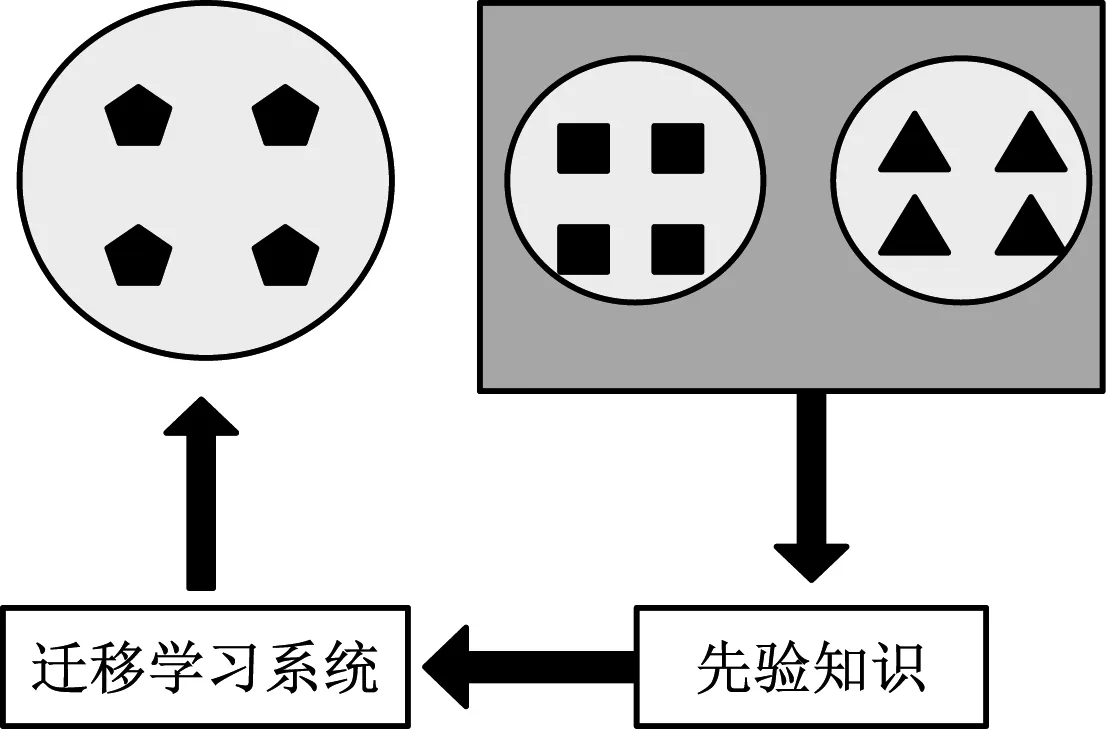
图1 迁移学习主要思想

在实际应用过程中，想要获得大量有标签目标样本数据较为困难，因此本文利用各领域的弱相似性[5]解决以上问题。

对于一个目标领域样本xt，将其类标号用yt表示，且PT(yt|xt)>0.5。若源领域样本xs的类标号与xt相同，则说明这两个领域间具有较大的相关性。与Ps(yt|xt)=PT(yt|xt)相比，上述为弱条件。据此，给出相关定义如下。

定义1PS(Q,M)和PT(Q,M)，其中Q表示样本变量，M表示类标号，如果以1-v为概率[6]进行推断，对于x～PS(Q)，在1-v的概率条件下，分布PS弱相似与PT，此时将v成为负相似度，v(PS,PT)。若分类器在PT中的泛化误差低于相对上界，可用L代替PT，即可获得定义2。

定义2 通过1-v的概率进行推断，对于(x,y)～PS(X,Y)，L(x)=y成立。则在1-v的概率条件下，称分布PS弱相似于PT，v是负相似度，记作v(L,PS,PT)。

当e的值较小时，L和目标领域的类标号函数相似，因此此时可以将v(L,PS,PT)视为v(PS,PT)的近似值。

设迁移分类学习的判别函数[7]为f(x)，设f(x)=w2x+b。在目标领域中f(x)的分类决策函数可以表示为：L(x)=sign(f(x))。假设L(x)的泛化误差足够小，则可以得出迁移学习中负相似度v(f,Ps,PT)，如式(1)：

v(f,PS,PT)=E(x,y)～Ps(I(yf(x)<0))

(1)

式中，I()表示指示函数，若条件成立其值为1，反之为0。利用样本中大量数据可获得式(1)的经验估计，如式(2)：

(2)

通过支持向量机法求解式(2)得到式(3)：

(3)

式中，w为间隔边界的距离，b为截距，ε为决策边界数。样本数量较小时，会发生f(x)的解泛化误差较大的情况。因此，通过弱相似度定义对f(x)进行额外约束，规定在源领域内，f(x)的负相似预估值v′(f,PS,PT)保持在较低水平，则优化问题可以表示为

(4)

εi≥0,i=1,2,…,m

式中，CS表示平衡参数。v′(f,PS,PT)为非凸函数，直接优化该函数较为困难。因此，采用损失函数进行替换。当yf(x)<0时，函数中的x会被错分，导致yf(x)的绝对值和经验风险较大，为解决以上问题，使用V(f,PS,PT)代替v′(f,PS,PT)，替换后其表达式如式(5)：

(5)

在优化目标中新增了V(f,PS,PT)，使在迁移学习的过程中能够使用源领域数据帮助训练[8]。对于目标领域，规定样本点只能落在最大间隔平面的外侧。

1.2 网络身份双向认证

在迁移学习的过程中，不同的特征值产生了不同的有限域[9]，且不同有限域中的通用算法也不相同，因此发挥出的运算性能也各有不同。通常情况下，在加密体制中的有限域为大素域GF(q)与特征2域GF(2m)。由于大多数系统对储存空间、处理速度和安全性有特殊要求，特征2域GF(2m)作为一种二进制域更容易在系统中快速实现。因此，本文将迁移学习中的大素域GF(q)与特征2域GF(2m)相结合作为身份双向认证的有限域。

首先选取相关参数：D=(q,a,b,p,n,h)或D=(m,f(x),a,b,p,n,h)。为使加密机制更为高效，对算法中相关参数进行限制。

(1) 有限域GF(2m)，q=2m，m表示正整数。

(2) 限制参数a、b，首先定义有限域GF(q)上的曲线E为：Y2=X3+aX+b(p>3)，Y2+XY=X3+aX+b(p=2)。

(3) 定义p为基点，n是素数，为基点p的阶。

(4) 定义h为余因子，通过曲线的阶与n相除获得，即h=E(Fq/n)。

(5)f(x)表示二进制多项式。

在身份认证的过程中，通过确定有限域内椭圆曲线参数，得到一条更适用于网络身份认证的曲线和基点。认证标签身份前，需要鉴别读写器身份是否被伪造。鉴别步骤如下。

步骤1 系统初始化。该步骤完成了相关参数确定同时生成秘钥，为下一步认证做准备。操作流程如下。

在GF(2m)中确定一个曲线E(Fq)。

在区间[1,n-1]内，通过随机的方法筛选出整数X，将其设置为私钥。将Y设置为公钥，利用私钥则可计算出公钥得具体数列，此处利用了求解离散对数问题较为困难的观点[10]，使得在已知公钥Y的条件下，攻击者依然不能获得私钥X。

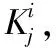
保密X私钥，公开公钥Y。

步骤2 读写器身份认证。为杜绝系统中出现仿冒读写器，因此验证标签身份前，首先完成读写器的身份验证。

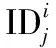
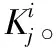
2 仿真实验

实验环境为i7处理器，内存容量为8 G，操作系统为Windows 10。仿真采用了基于迁移学习的网络身份双向认证技术，主要对网络身份认证技术的防御性能以及同步性能进行比较，相关的参数设定：选择特征2域中椭圆曲线参数，标签基点数量为170。

2.1 防御性能测试

为验证本文身份验证方法的有效性和安全性，采用不同的方法对系统进行恶意攻击，随后将身份认证的安全性能与文献[1]、文献[2]方法进行比较分析，其结果如表1所示。

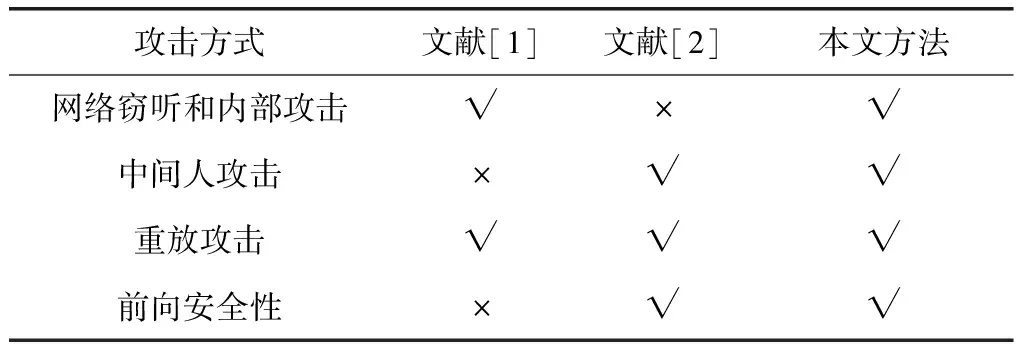
表1 不同认证方法的防御性能对比

从表1中可以看出，本文方法能够阻止以下攻击。

(1) 网络窃听和内部攻击：这是由于数据库内并没有储存相关的身份信息，只储存了公钥列表，所以即使是内部人员也无法通过公钥和获得私钥进行身份欺骗。

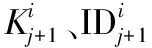
(3) 中间人攻击：在双向验证的过程中，若攻击者截获的了阅读器发送给标签的信息，试图使用该信息通过验证也是不可行的，这是由于本文对2个身份均有验证，单独获得一方信息无法认证成功。

由此证明了本文身份认证方法能够成功拦截多种恶意攻击。

2.2 同步性能测试

为验证本文方法的同步性能，输入60s内170个标签身份的验证口令，采用本文方法与文献[1]、文献[2]方法分别对其进行认证，将3种认证方法的同步性进行比较，其结果如图2所示。

图2 同步性能对比

根据图4可知，本文方法在对身份进行验证时，相同时间内验证的口令个数较多，验证速度较快，证明其口令同步性较高。

3 总结

本文结合迁移学习理论提出了一种基于迁移学习的网络身份双向认证技术。本文方法只有认证通信双方均为合法的，才能进行通信连接。并且通过实验对其防御性能和同步性能进行分析，分析结果表明本文方法具有一定抗攻击性和同步性，能够较好的拦截多种攻击，确保用户的网络通信安全。