基于聚类算法的电网分布式增值业务数据集成系统
陈竞,李宇远,杜杰
(南方电网数字电网研究院有限公司, 广东, 广州 510670)
0 引言
对于电网的孤立、异构信息,许多专家进行了研究[1]。通过电网数据交换,解决数据孤立性强、异构性强的问题,以逻辑和物理的形式采集格式和属性的电网数据,为电力企业方便管理提供全面的电网数据,从异构和孤立的数据中,将具有关联属性的数据区分并聚集的过程[2-3]。同时,k-medoids聚类算法具有运算速度快,使用于大型数据的优点,其利用聚类中心点距离削弱电网分布式增值业务数据异常值的影响,计算精度较高。因此,本文结合k-medoids聚类算法,设计一种电网分布式增值业务数据集成系统,为电力企业提供充分的电力数据呈现形式。
1 基于聚类算法的电网分布式增值业务数据集电网分布式增值业务数据集成系统
1.1 系统整体架构
本文依托Spark平台构建电网分布式增值业务数据集成系统(下文简称系统)。Spark平台是通过内存计算的大数据分布式计算框架[4],具备处理大数据实时性能力且其容错性和伸缩性均较强,其兼容性也较好,可安装在厂家以及型号不一的硬件设备上组成集群。依据分层和针对组件设计理念,将系统分为4个层次,系统具体结构如图1所示。
图1中,该系统由应用层、云服务层和基础平台层组成。其中,应用层使用B/S结构,通过MVC模型内前端开发工具包完成界面设计,为电网用户与电网企业管理人员提供可操作页面,如聚类任务、集成任务、系统性能查看等等;应用层利用前端应用服务器与数据库服务器,通过HTTP等技术实现分布式增值业务数据交互功能,后端则通过Web服务与云服务层和基础平台层相连接;云服务层则为系统提供聚类分析服务、权限查询等功能,设置在后端服务器内,通过技术手段完成系统接口形式的封装服务功能,且应用层可自由调取该服务[5];基础平台层为云服务层提供计算服务,该层利用Hibernet框架实现分布式增值业务数据传递,为系统供给分布式增值业务数据持久化功能,并以接口的形式与Spark平台的集群形成连接,为电网增值业务数据库提供接口,可实现系统的管理、数据访问与处理等功能。
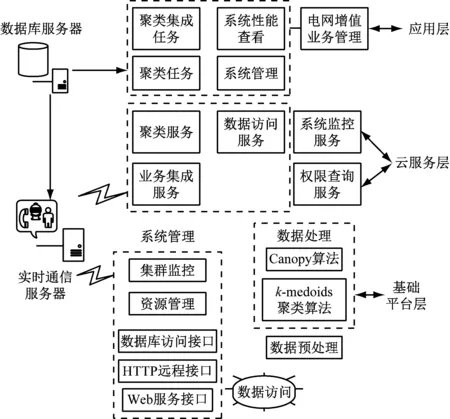
图1 系统结构
1.2 基于Canopy的电网分布式增值业务数据集成算法
1.2.1 Canopy算法
在分布式增值业务数据集成时,由于数据构成繁琐设置合适的类簇数值难度较大[6],因此本文利用Canopy算法计算最佳类簇数值,在对电网分布式增值业务数据聚类处理之前,需提前设定类簇数值,保证聚类效果,使其适用于海量数据处理,具备较强的伸缩性。
令T1、T2孤立表示电网分布式增值业务数据的粗略划分,Canopy算法聚类划分示意图如图2所示。
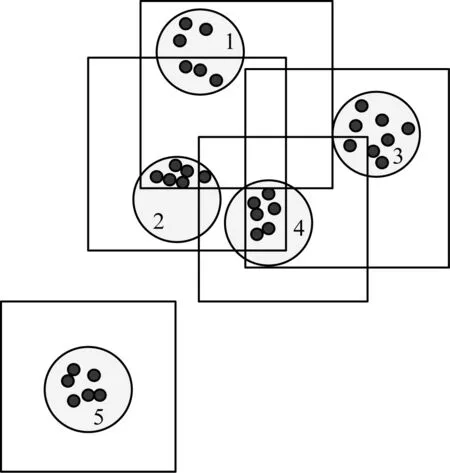
图2 Canopy聚类过程示意图
在图2中,方框表示距离阈值T1,圆圈表示距离阈值T2。其中2个距离阈值利用交叉验证方式获取,Canopy算法将所有电网分布式增值业务数据均放在候选集内,该候选集内所有对象之间的Canopy,对比Canopy数值和距离阈值T1,当Canopy数值较离阈值T1数值低时,将Canopy添加到上图方框区域内,反之将Canopy放置于上图圆圈内,从候选集内删除,当所有电网分布式增值业务数据均被加入到Canopy内时,该Canopy的数量即为最佳类簇数量。
1.2.2k-medoids聚类算法
增值业务数据聚类中心选择非常重要,若聚类中心偏离情况严重,则聚类效果不佳且消耗时间过长,在此依据密度聚类理论,在较大程度避免噪声干扰情况下,增值业务数据的初始聚类中心获取过程如下。
令U表示增值业务数据集,该数据集内业务数据样本点由x表示,则以该点为圆心,半径为r的正整数所涵盖的圆形区域内数据点的数量为点密度由Dens(s)表示,增值业务数据集内中样本点密度的平均值称为均值点密度由AvgDens表示,则有:
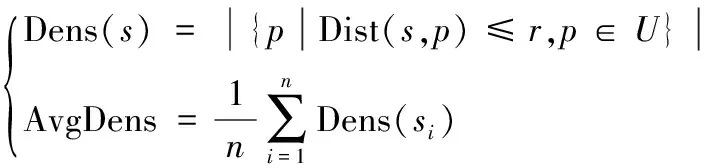
(1)
式中,圆心与增值业务数据集内样本点p的欧式距离由|Dist(s,p)表示,圆心半径r=α*a,其中α为常数,a为增值业务数据集样本点之间距离平均数值,其计算公式如下:
(2)
式中,i=1,2,…,n,j=1,2,…,n。
令CDens(ui)表示增值业务数据集内类簇包含样本点数量占总样本点数量比值即类簇密度数值,其计算公式如下:
(3)
在k-medoids聚类算法中,通过获取增值业务数据样本内样本点的密度,依据该点密度属性选取其初始聚类中心,其流程如下。
Step1 获取增值业务数据样本内,多个样本点之间距离。
Step2 计算样本点密度Dens(si)、点密度平均值AvgDens数值,将密度数值高于点密度平均值的样本点作为核心点,将其聚集一起构成集合T,密度数值低于点密度平均值的样本点作为类簇内数据点。
Step3 将包含核心点的类簇合并。
Step4 计算所有类簇密度数值CDens(ui),以前k个类簇密度较大的簇作为初始聚类中心基础数据,计算该k个类簇中心点,并将该类簇中心点作为增值业务数据的初始类簇中心。
令类簇ui内具有m个数据点,则数据点集合为{s1,s2,…,sm},由ni表示该类簇的中心点,其计算公式如下:
(4)
式中,k表示可变参数。
类簇内样本点的距离计算公式如下:
dist(s,o)=
(5)
式中,o表示与样本点x相邻样本点。
通过上述4个步骤,可有效获取增值业务数据集的初始聚类中心,从而实现电网分布式增值业务数据并行聚类,该算法使聚类范围缩小的同时也使聚类时间得到降低。
1.2.3 电网分布式增值业务数据集成模型
电网分布式增值业务数据集成是依据同类思想,将所有数据重新组合,使位于同簇内的数据属性相同或相似的过程。依据Canopy算法获取的类簇数量和k-medoids聚类算法获取的数据初始聚类中心,利用Spark平台内分布式框架功能建立电网分布式增值业务数据集成,该模型总体流程如图3所示。
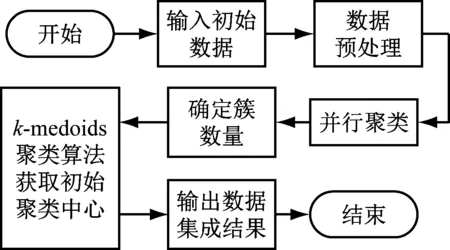
图3 电网分布式增值业务数据集成模型流程示意图
电网分布式增值业务数据集成模型先将增值业务数据进行归一化处理后,利用Canopy算法计算类簇数量后,使用k-medoids聚类算法获取初始聚类中心后完成数据并行聚类,利用模型输出最终电网分布式增值业务数据集成结果。
2 实例测试与结果分析
本文系统运行环境为Intel八核处理器、12G DDR3内存、CentOS 6操作系统,200 M网络交换机,Spark平台版本为Spark Version 1.0。以某电力企业2020年的随机一个增值业务数据为实例测试对象,从多个角度对本文系统展开实际应用测试。测试过程如表1所示。
表1 实例测试数据采集与应用过程
2.1 聚类能力测试
从线程数量方面,测试本文系统聚类能力,设置不同线程数,且指定聚类数量为35个,统计本文系统在不同线程时,对该企业增值业务数据聚类消耗时间,结果如图4所示。
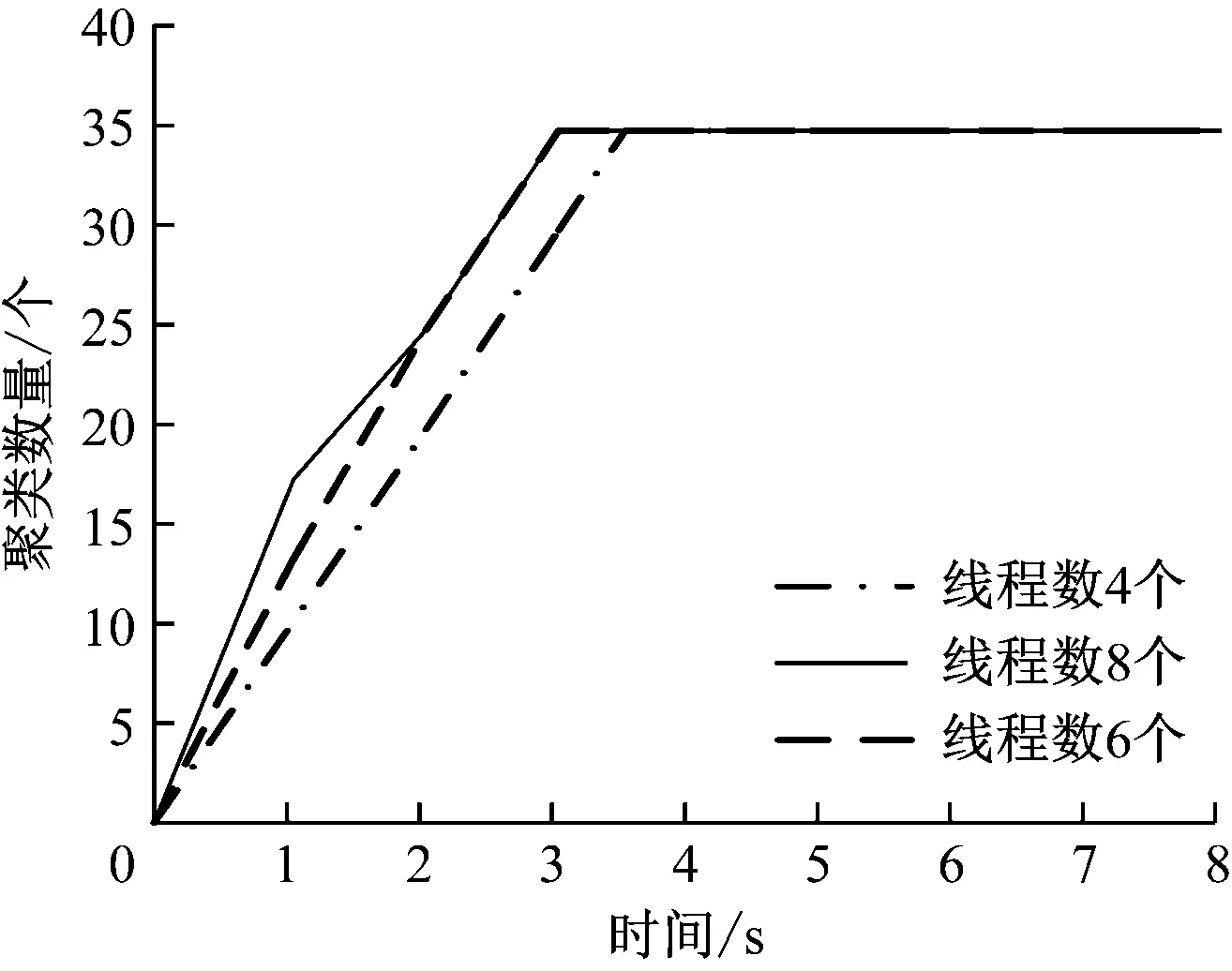
图4 不同线程数时聚类能力测试
分析图4可知,在给定聚类数值情况下,随着聚类时间的增加,不同线程数时聚类曲线均呈现迅速上升趋势。当达到给定聚类数值后,虽然系统线程数不同,但其聚类数量保持不变。其中,当线程数分别为6和8时,达到设定的簇数所需时间为3 s。当线程数为4时,达到给定簇数的时间比其他2种线程长0.3 s,且差异不大,表明该系统受线程数的影响较小,具有良好的聚类能力。
单从线程数量方面验证本文系统的聚类能力具有一定片面性,因此,取该增值业务数据大小为100 GB至1 000 GB的相关数据,测试本文系统在数据预处理、数据并行聚类等方面综合能力,结果如表1所示。
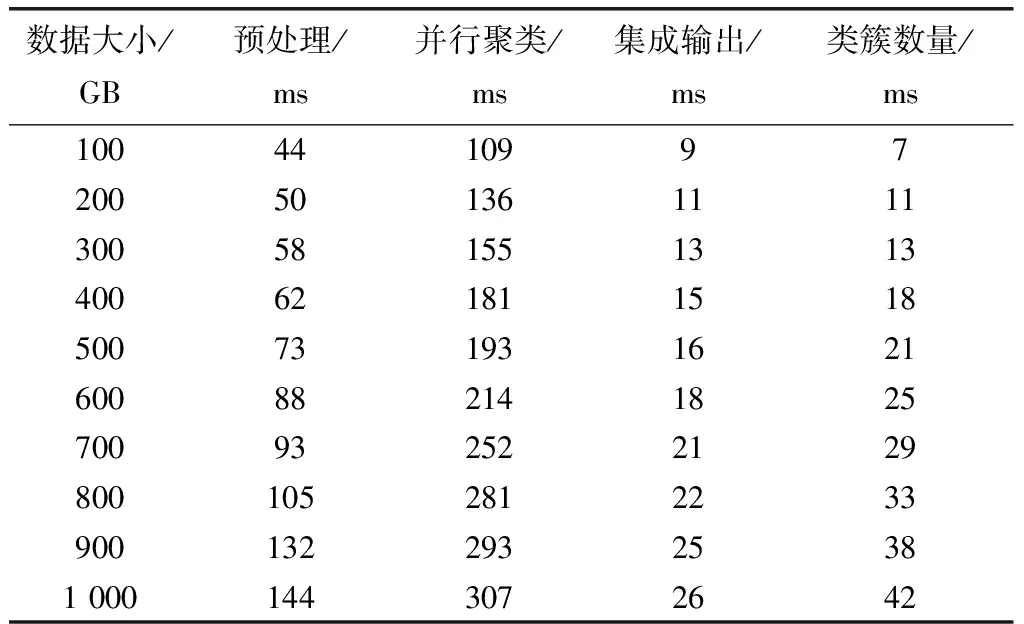
表1 综合聚类能力测试
分析表1可知,随着数据量大小的增加,系统对增值业务数据的预处理、并行聚类以及集成输出运行时间均逐渐增加,类簇数量也随之增加,其中在并行聚类时消耗时间较多,但运行时间上升不大。在数据量为1 000 GB时,其运行时间较数据量为100 GB时上涨1.81%,而数据集成输出时间较短,上涨幅度不大,类簇数量上升跨度较大,表明系统对企业增值业务数据属性划分精确,聚类准确性较高。在数据量为1 000 GB时,系统整体运行时间仅为7.95 min,聚类性能较好,且当数据量较大时,系统运行时间较少。
2.2 系统集成性能
测试不同文件大小时,系统串行数据集成与平行数据集成时间比值,即系统加速比,该数值表示系统运行时间降低系统性能提升情况,加速比是衡量系统性能的重要指标之一,以加速比为实例测试指标,测试系统集成性能,结果如图5所示。
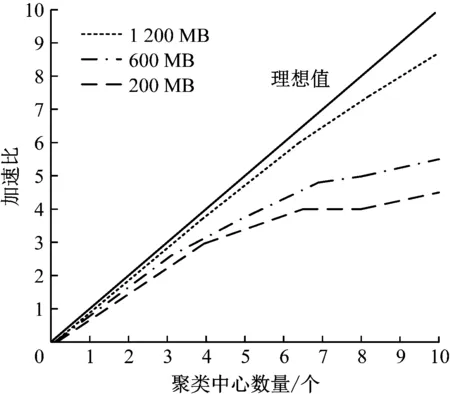
图5 系统集成性能测试结果
分析图5可知,系统在企业增值业务数据为1 200 MB时,线性趋势较强,而在数据量分别为200和600个时,在聚类中心数量在7个之前,系统加速比曲线表现为线性关系;在聚类中心数量超过7个之后,系统加速比曲线出现轻微波动,说明增值业务数据越大,系统加速比曲线线性关系越好,越接近理想值。
3 总结
电子信息技术与大数据技术在提升各个领域信息化的同时,也为企业数据管理增加了一定难度,尤其是电力企业,其数据来源众多且孤立,因此,电力企业对数据集成需求度极高。本文针对此类情况设计了基于聚类算法的电网分布式增值业务数据集成系统,经过多角度测试,本文系统在不同线程数量情况下,给定聚类数量消耗时间仅为0.3 s,受线程数量影响较小,聚类能力好,增值业务数据越大,系统加速比曲线线性关系越好,系统集成性能得到保证。

