基于电流监测的低压配电网拓扑识别方法

沈超，朱振，俞家融，陈亦寒，周鹏，张华锋

(1.国网江苏省电力有限公司无锡供电分公司, 江苏, 无锡 214000；2.南京南瑞信息通信科技有限公司, 江苏, 南京 211300)

0 引言

随着电力技术的进步和电网中新的复杂元件的增加，配电网的复杂性日益增加。一般情况下，电力系统的控制和监测集中在发电、输电和高压配电各级。随着太阳能、风能等间歇性分布式能源的有源配电网和电动汽车等插入式装置的出现，对低压配电水平的控制提出了更高的要求[1]。

一些低压用电设备采用单相供电，它们由配电变压器三相中的一相供电。这些用户的相位连通性也是网络拓扑信息的一部分。该信息对于维持配电变压器和配电馈线三相的负载和电压平衡非常重要。变压器和馈线上的不平衡负载会导致更高的铜损耗和电压降，从而影响资产的使用寿命。

低压配电网的拓扑结构使其众多节点[2](如馈线、配电变压器、配电盘和用户)之间具有连通性。基础网络拓扑结构的信息对于有效整合可再生能源和有效管理配电网中断非常有用。因此，在状态估计、故障定位、电压无功控制、需求响应等低压配电领域中的各个方面，准确的网络拓扑信息至关重要[3]。如果对网络拓扑的了解不正确，那么这些应用就会产生不正确的结果。因此，必须经常识别网络的拓扑结构。然而，在实践中，拓扑识别对于配电系统来说是一项具有挑战性的任务，因为测量值有限，而且配电馈线上的开关和断路器的状态信息不可用或不可靠。此外，当一个相位跳闸时，用户可能具有在相位之间切换的功能，从而改变拓扑结构。同时，由于网络重新配置、维修、维护和负载平衡而发生的变化，网络拓扑信息可能并非始终准确可用[4]。

为了准确识别网络拓扑信息，国内外众多学者提出了许多网络拓扑测量方法。周青等[5]针对配电网故障点定位速度慢、对电网造成冲击等问题，提出了一种基于智能配变终端的配电网故障区段判断方法。在获取台区拓扑的基础上，提出了一种利用智能配变终端边缘计算能力的矩阵判别法，根据判断矩阵实现故障区段快速定位。杨志淳等[6]介绍了一种基于数据关联分析的低压配电网拓扑识别方法，在每类台区内筛选特征电压序列，并利用Tanimoto相似度系数计算各分组内配电变压器、分支箱、表箱、用户智能电能表之间相关性和非相关性，从而实现低压配电网拓扑识别。ZHU等[7]在原有网络的基础上增加一个调节机制，构造一个由孤立节点组成的辅助网络。通过调节网络和辅助网络之间的外部同步，证明可以识别原始网络。JAHANDARI等[8]提出了一种数据驱动的算法来揭示网络的拓扑结构并识别连接的动态性。作者将拓扑识别问题归结为一个基于压缩感知和匹配追踪的结构化稀疏信号恢复问题。当有足够的数据可用时，该算法能很好地识别一般网络。作者通过对电压测量值进行相关分析来重建电网拓扑。

本文提出了一种改进的基于电流检测的拓扑识别算法，在安装了线路电流传感器的几条线路上进行线路电流测量，同时考虑测量时存在的误差，并对优化函数进行更新，以适应测量误差对拓扑识别准确率造成的影响。

1 拓扑识别模型

本文中假设所有交换机都关闭，所有线路和节点都遵守基尔霍夫电流定律[9]，每个节点的电流注入等于与该节点连接的线路相关的电流总和，故有

(1)

由于流过两个节点之间线路的电流取决于线路的开关状态、两个节点的电压和线路的导纳。根据基尔霍夫电压定律，有

Iij=sij(Vi-Vj)yij

(2)

其中，sij为线路{i,j}开关状态的二进制变量。如果线路{i,j}可用，sij为1；否则为零，用以确保Iij为零，表示该线路已停止服务。

根据电功率公式，节点电压Vi与电流注入Ii之间的关系描述为

(3)

其中，bi为节点i开关状态的二进制变量。如果节点i连接到网格，则bi为1；否则为零，表示网络中存在孤立节点。

综上，拓扑识别问题可总结为一个优化问题，具体定义为

(4)

Iij=sij(Vi-Vj)yij

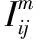
该优化问题倾向于将式(1)～式(3)计算的线路电流相量与线路传感器测量的相量相匹配。所有线路{i,j}的二进制变量sij的解指示线路交换机的状态，因此其表示网络拓扑。对于所有节点i的二进制变量bi的解，它们指示一个节点是否连接到网络的其余部分。因此，该值表示中断区域。

2 拓扑识别方法

图1为拓扑识别方法运行流程图，关键过程包括两个步骤：传感器布置和计算测量误差。

图1 拓扑识别过程

2.1 可观测性及传感器布置

可观测性分析和传感器布置通常针对特定应用进行研究，在本文中，可观测性分析涉及以下几个方面。为了确定网络的拓扑结构，需要知道交换机的状态。开关断开的线路没有电流，因此通过估计线路电流来获得开关的状态，从而最终确定网络的拓扑结构。因此，可观测性分析可以归结为以下问题：确定需要多少个线路传感器(以及在什么位置)来解决本文中的拓扑识别问题。

令电力系统中有N个节点和L个支路电路。为估计支路电流，至少需要L个独立的方程来求解。因此，为了得到L个独立方程组，需要L-(N-1)个附加的独立方程组，可通过测量L-(N-1)个线路电流获得。

综上，为了顺利观测支路电流，本文规定在配电网的每个独立回路中至少放置一个线路电流传感器，以此来确定配电网的拓扑结构。

2.2 测量误差

到目前为止，假设线路测量和节点视在功率测量为理想测量环境，即不存在测量误差。然而，这一假设在实际情况中未必成立。因此，为解决测量误差，本文将低压配电拓扑识别优化函数进行改进，提出将注入电流约束以惩罚项的形式添加到目标函数中，故新的目标函数更新为

(5)

通过定义辅助变量Gi和Hi，并添加以下新的线性约束来处理非线性问题，

(6)

Gi≥0,Hi≥0

上述优化问题的解的存在性或唯一性无法从理论上得到证明。但可以得知，即使在测量值由于重大误差而远离其真实值的严重条件下，也总能得到可行的解。

3 实验仿真

本节将通过一个应用于IEEE33总线测试系统证明所提拓扑识别方法的有效性。馈线的连接方式如图2所示。由图2可知，网络中有21个交换机，其中实线表示常开线路(馈线4,6,7,9,10,11,12,14,15,16,17,18,26,28,30,32)，虚线表示可关闭电路(馈线33,34,35,36,37)。因此网络可以创建221个不同的拓扑结构，本节选择了65个拓扑结构，包括50个径向、10个环路和5个岛。选择这些拓扑的标准主要是确保所有三种类型的拓扑，即径向拓扑、环路拓扑和孤岛拓扑，同时它们涉及网络中的所有独立环路。

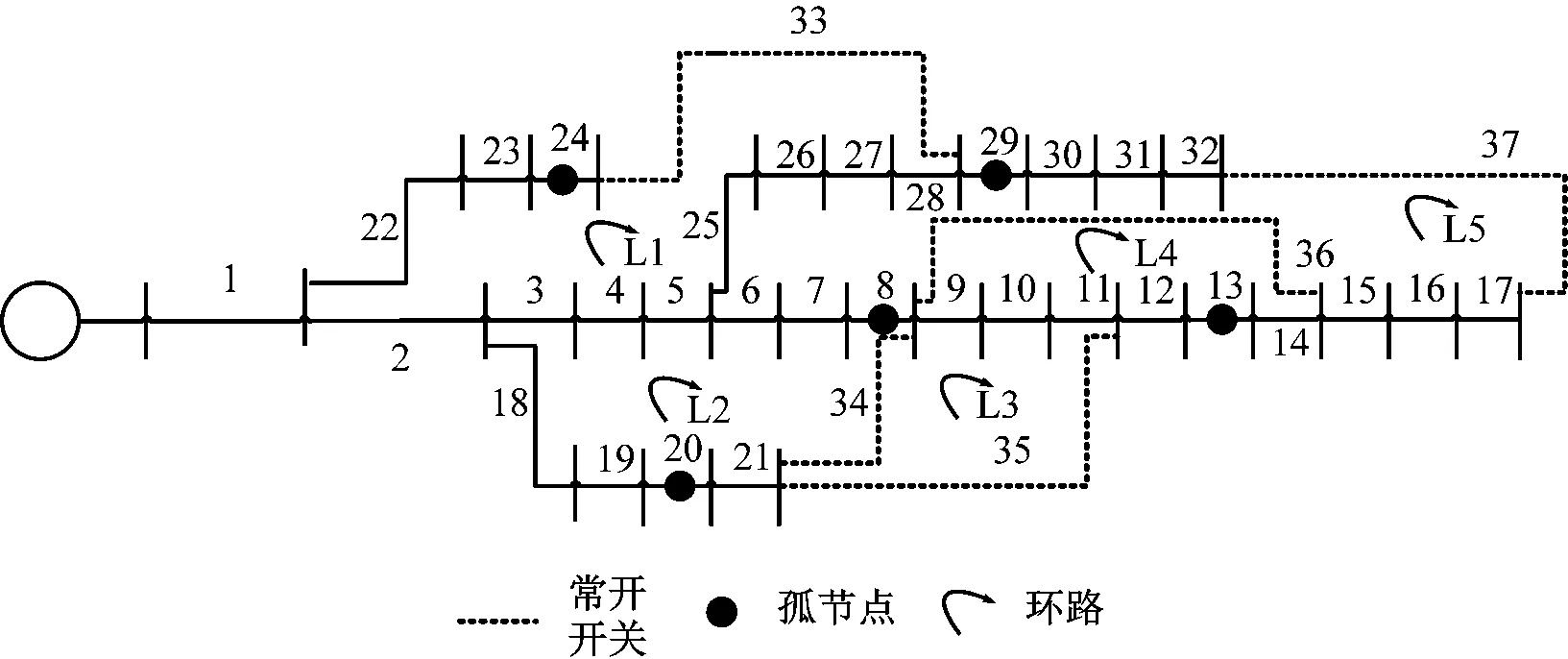
图2 馈线连接示意图

在MATLAB中进行了网络仿真和拓扑识别算法的实现，并用LINGO求解了式(6)的优化问题。在仿真中，假定测量值的构造如下：

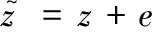
(7)

(8)

式(8)确保了99.7%的误差值落在真值±ηi%内。同理，拓扑识别算法的准确度以百分比表示为

(9)

其中，NT为网络中拓扑识别的总个数，NAT为网络中正确识别拓扑的个数。

图3为测量装置数量与拓扑识别准确率的关系。由图3可以看出，随着测量装置数量不断增多，拓扑识别准确率不断提高；此外，当测量误差不断升高，拓扑识别准确率逐次降低。实验结果符合实际规律，且进一步验证了本文所提拓扑识别算法能够有效针对测量误差情况，当测量误差在真值±50%，测量装置数量超过20个时，拓扑识别算法准确率也能达到95%。

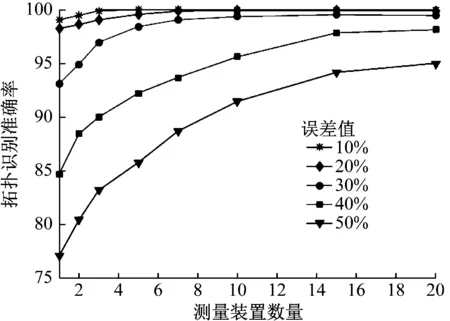
图3 测量装置数量与拓扑识别准确率的关系

图4为本文方法与基于整数规划方法[10]和基于连通性[11]方法在不同测量误差下，拓扑识别准确率的对比结果。由图4可以看出，随着测量误差不断升高，本文方法较其余两种方法相比，基于连通性方法效果最差；基于整数规划方法在误差较小时识别准确率较高，然而随着误差不断增加，算法性能逐渐降低。分析原因，主要是因为其余2种方法未考虑误差情况，当测量误差较大时，将对优化结果产生不可估量的影响。

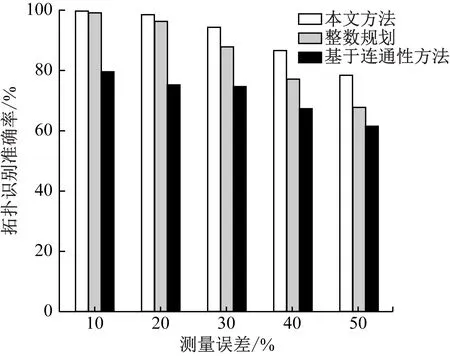
图4 不同算法下拓扑识别准确率对比结果

4 总结

本文对低压配电系统中拓扑结构进行了研究，在研究拓扑识别模型基础上，提出了拓扑识别中可观测性及传感器配置方案，并针对系统中出现的测量误差提出了有效的解决方案。通过仿真分析结果表明，本文所提方法在应对低压配电系统拓扑识别时出现的测量误差具有一定效果。当测量误差在真值±50%，测量装置数量超过20个时，拓扑识别算法准确率也能达到95%。实验结果进一步验证了本文所提方法的实用性。

本文在处理拓扑识别时，假设干扰为正态分布模型，在一定程度上能够反映实际情况。然而在实际过程中，配电系统干扰除了受到随机误差外，还存在延迟、系统误差等情况，这也是将来研究的重点与方向。