基于人工智能技术光通信传感器的自动控制

周滟

(四川信息职业技术学院,网络与通信学院， 四川，广元 628040)

0 引言

随着光理论和通信技术的不断发展、成熟，出现了光通信传感器，相对于其他类型的传感器，光通信传感器的抗干扰能力更强，更加稳定可靠[1-3]。随着光传输网络快速发展，人们对光通信传感器的性能要求越来越高，同时受到外界环境的影响 ，光通信传感器的输出结果有时受到干扰，为此需要对光通信传感器进行自动控制，提高其输出效果[4-6]。

针对光通信传感器自动控制问题，国外的研究历史比较长，光通信传感器自动控制技术也比较成熟；国内光通信传感器自动控制的研究历史比较短，控制技术还不太成熟，光通信传感器自动控制方法非常局限[7-9]。如：有学者[10-11]提出了采用实时功率反馈的光通信传感器控制方法，该方法控制波形有非线性失真，导致光通信传感器控制效果不佳；有学者[12]提出了波前误差的建模的光通信传感器控制方法，由于该方法计算复杂导致光通信传感器自动控制精度低；近些年，有学者[13-15]提出了基于遗传算法、粒子群算法等光通信传感器自动控制方法，它们通过不断的迭代找到光通信传感器控制参数最优值，从而实现光通信传感器自动控制。但在实际应用这些算法还存在一些不足，如搜索效率低、光通信传感器自动控制效果有待进一步改善。

因此,本文研究基于人工智能技术的光通信传感器自动控制方法。该方法可按照光通信传感器的输出性能、粒子激励调整参数，增强参数自适应匹配，实现光通信传感器的自动控制。

1 基于人工智能技术的光通信传感器自动控制

1.1 改进粒子群优化算法

粒子群算法是一种模拟鸟群搜索食物的人工智能技术，粒子群优化算法解决群体问题，群体内个体转到最佳位置是按照对环境的适应度实施的移动，在多维空间内搜索飞行粒子，按照经验对粒子飞行实施微调。

1.1.1 传统粒子群优化算法

在1个n维搜索空间内，群体由m个粒子构成，第i个粒子最佳位置为Pi=(pi1,pi2,…,pin)；第i个粒子的位置为Xi=(xi1,xi2,…,xin)，其中i=(1,2,…,m)；粒子速度为Vi=(vi1,vi2,…,vin)，对应的适应值在最小化问题中与目标函数值呈反比。f(x)表示最小化的目标函数，通过目标函数得出粒子i的最佳位置计算公式为

(1)

式中，t表示迭代次数。通过单个粒子最佳位置计算全局最佳位置，即群体内全部粒子路过的最佳位置，计算公式为

Pg(t)∈{P0(t),P1(t),…,Pm(t)}|f(Pg(t))=

min{f(P0(t)),f(P1(t)),…,f(Pm(t))}

(2)

基本粒子群进化方程，如式(3)：

(3)

其中,rand1()、rand2()表示相互独立[0,1]间的随机数,a1表示“认知”加速常数,a2表示“社会”加速常数,vi(t)表示第t代第i个粒子的速度,xi(t)表示第t代第i个粒子的位置。

随机生成粒子群初始速度与位置，依据式(3)实施迭代求出最优解。在每代内，粒子由全种群的最优解与粒子自身的最优解组成的跟踪极值。利用陨性权重对粒子群进化算法进行优化和改进，具体如下：

(4)

式中，w表示惯性权重，采用该方法是为了提升算法的查询能力及结果的精确度。当惯性权重低时，局部收敛能力高；当惯性权重高时，全局收敛能力较佳。线性递减权重策略具体如下:

(5)

利用引入收缩因子的粒子群优化算法模型，控制微粒的飞行速度，该模型表示如下：

(6)

其中,c为收缩因子。传统算法对速度进行控制，但是该粒子群算法也存在不足，如收敛过早，得到的解是局部最优解等。

1.2 本文改进的粒子群算法

在传统算法的基础上，可以采用协同进化算法提升全局收敛效率。通过将整个群体分成多个子群体，各子群体内都有独立个体的解。局部搜索全部子群体发现最佳个体迁移，以此完成共享信息进化。粒子群划分为多个子群体，根据协同进化算法的划分方法，提出基于专业化分工的策略，提高粒子群的群体适应环境能力。专业化分工的策略：设定m个粒子构成粒子群，将粒子群分为开采者(Q1)子群体、开采者(Q2)子群体、探索者(Q3)子群体。

当惯性权重为0.3时，构成Q1子群体，此时子群的收敛迭代进行速度最快，具体为

(7)

w=0.3

通过“社会模型”构成Q2子群，收缩因子为0时，即c=0，当惯性权重为0.7时，Q2子群开始配合Q1进行迭代。此时,Q2子群进行收敛的最佳时机，具体为

vij(t+1)=wvij(t)+a2rand2()(pij(t)-xij(t))

(8)

w=0.7

当惯性权重为0.9时，形成探索者Q3子群。此时,Q3通过全局搜索能力进行迭代，三者同时进行，运行效率最高的时候，具体为

(9)

w=0.9

专业化分工的策略流程：将群体分成几个子群体，对子群体实施专业化社会分工，采用“社会”加速常数a2和全局最佳位置，实现子群体间的粒子信息交换。开采者Q2子群体实施全局搜索，在个体与全局最佳位置的小范围里搜索，发现新的最佳位置并收敛到这个最佳位置，实现子群体Q2分工。开采者Q1子群体实施局部快速搜索，在个体与全局最佳位置的小范围里搜索，同时快速收敛实现子群体Q1分工。探索者Q3子群体实施全局搜索，大范围搜索个体与全局最佳位置，发现新的最佳位置，使子群体Q1和子群体Q2移动至新的最佳位置实现子群体Q3分工。

为了提升粒子群的寻优效率，采用专业化分工的改进策略实施群体划分，各子群体专业分工协作完成寻优。

1.3 人工智能技术的光通信传感器自动控制流程

光通信传感器自动控制的输出向量与输入向量分别用y(t)、r(t)描述。因为光通信传感器自动控制的输出向量与输入向量间存在误差，误差用b(t)=y(t)-r(t)描述。采用人工智能技术中的粒子群优化算法实施光通信传感器自动控制，增强光通信传感器自动控制精度。基于人工智能技术的光通信传感器自动控制流程，如图1所示。

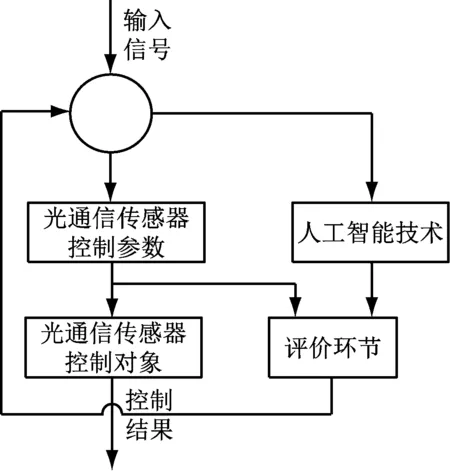
图1 人工智能技术的光通信传感器自动控制流程

通过图1可知,基于人工智能技术的光通信传感器自动控制流程如下。

step1 采用改进粒子群优化算法设计光通信传感器自动控制的传递函数，传递函数用式(10)描述：

(10)

step2 设置光通信传感器自动控制的参数范围。

step3 将相关参数实施初始化，光通信传感器自动控制的参数用1个粒子描述。

step4 计算出光通信传感器自动控制的期望输出与实际输出值间的误差b(t)。

step5 按照误差b(t)调整光通信传感器自动控制的参数。

step6 为了增加迭代次数，需要更新操作粒子状态。

step7 种群和粒子的最优状态是按照目标函数值实施更新操作。目标函数，用式(11)描述：

(11)

step8 若迭代次数大于改进粒子群优化算法设置的最大迭代次数，则结束运行。

step9 按照最优控制参数实施光通信传感器自动控制。

2 仿真实验结果分析

2.1 实验环境设置

为了测试人工智能技术的光通信传感器自动控制效果，选取一个通信传感器作为测试对象，采用MATLAB 2017作为仿真工具箱，选择遗传算法的光通信传感器控制方法、传统粒子群算法的光通信传感器控制方法进行对比测试。参数设置：粒子群规模是100;惯性权重w=0.5;最大迭代次数是200;“社会”加速常数a2和“认知”加速常数a1为a1=a2=1.3;收缩因子c=0.5。光通信传感器的一组参数设定为K1、K2、K3。

2.2 控制参数分析

运用本文方法优化光通信传感器目标函数ITAE变化曲线如图2所示。本文方法优化3个参数变化结果如图3所示。对图2和图3结果进行分析可知，目标函数ITAE在优化过程中逐渐降低，采用本文方法收敛速度快，在第100次迭代时完成收敛，本文方法自动控制下，可为光通信传感器选择合理的K1、K2、K3传递函数，使光通信传感器的K1、K2、K3参数与期望参数值一致，在第100次迭代后，参数值趋于平稳控制效果好。

采用3种方法对光通信传感器自动控制参数与目标函数调整对比结果如表1所示。对表1进行分析可知,采用本文方法对光通信传感器参数实施优化时，结果要优于遗传算法、传统粒子群算法的控制结果，在相同的迭代次数下，本文方法比遗传算法、传统粒子群算法更能快速找到最优值和最优状态，并与期望参数值及目标函数一致。

2.3 控制精度分析

采用本文方法与幅度调制方法、波前误差的建模控制方法分别对一个光通信传感器的100个数据实施10次实验，分析光通信传感器自动控制精度，对比结果如图4所示。由图4对比结果可知,本文方法比其他2种方法具有显著优势，采用本文方法对光通信传感器自动控制平均精度为95%，比遗传算法、传统粒子群算法的控制精度高，有效降低了光通信传感器自动控制误差，本文方法获得了理想的光通信传感器自动控制效果。

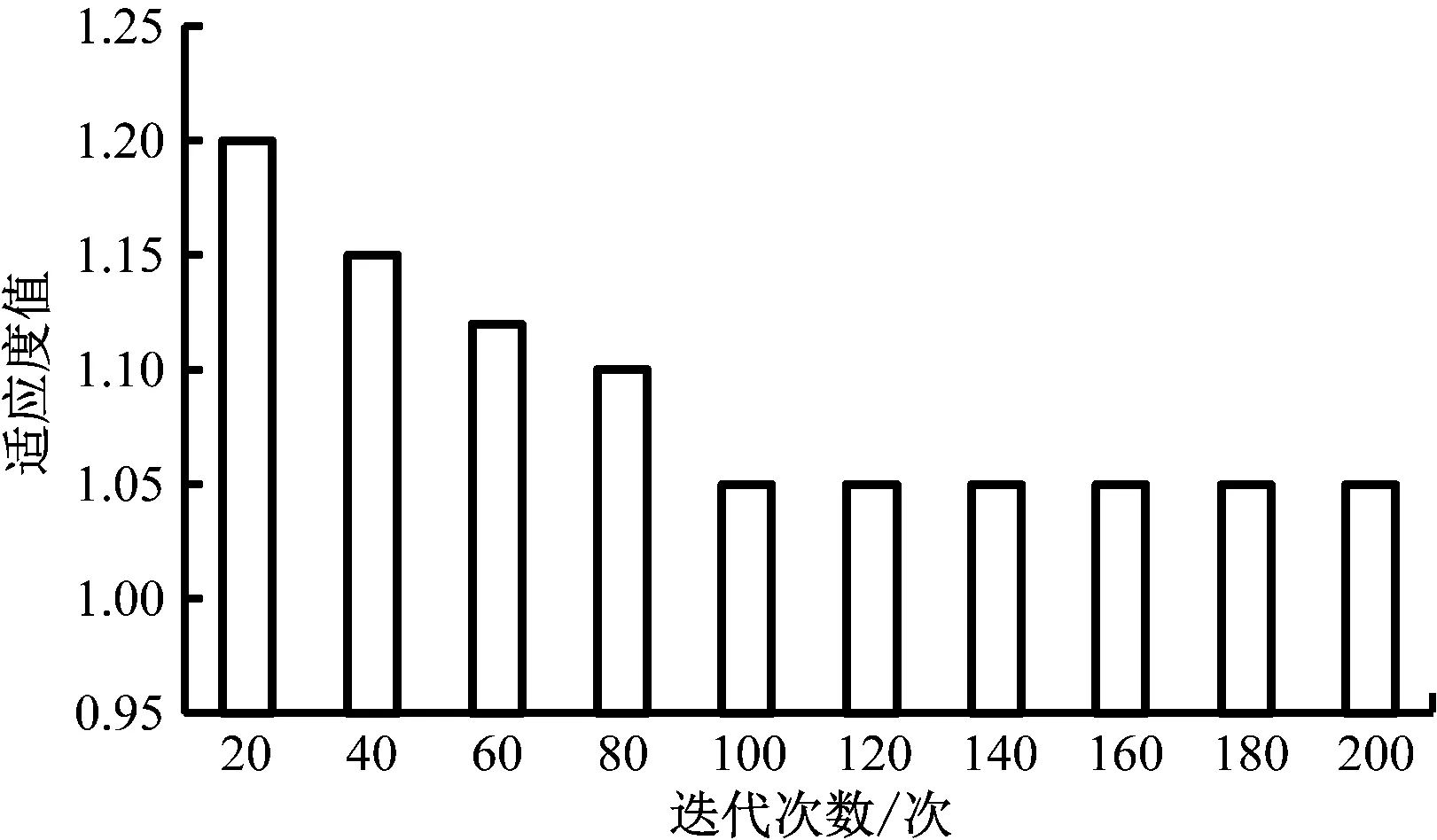
图2 目标函数ITAE变化曲线

图3 K1、K2、K3优化曲线

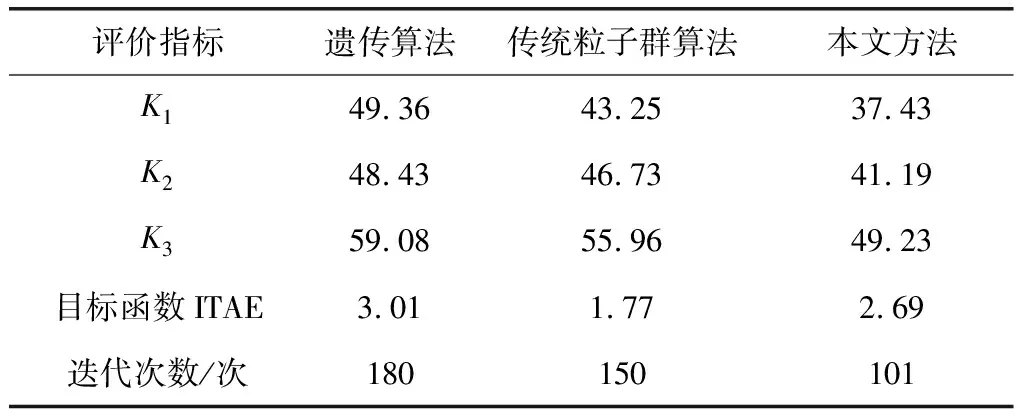
表1 3种方法参数与目标函数对比结果

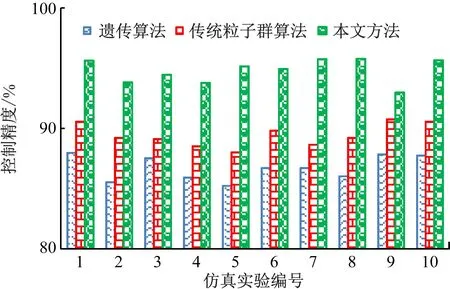
图4 控制精度对比

2.4 控制效率分析

统计采用3种方法光通信传感器自动控制时间，如图5所示。由图5的对比结果可知,本文方法对光通信传感器的平均控制时间短，比采用遗传算法、传统粒子群算法的控制平均控制时间减少很多。因此，本文方法对光通信传感器自动控制时间最短、速度最快、效率最佳。

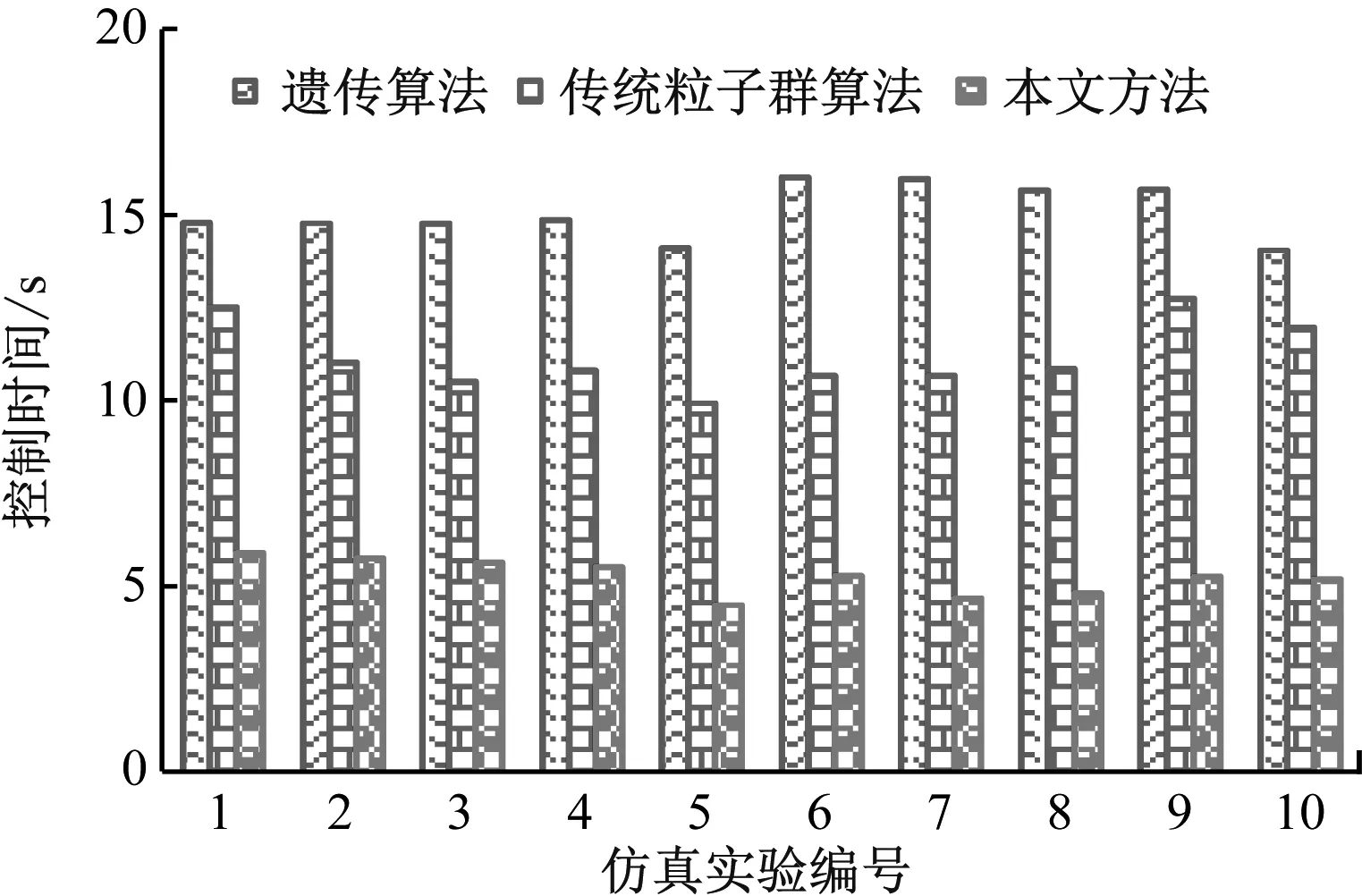
图5 控制时间对比结果

2.5 方法的稳定性分析

采用本文方法与遗传算法、传统粒子群算法在光通信传感器自动控制稳定性实施对比实验，设置3种方法的工作时间均为120 s，每间隔10 s记录一次数据结果，稳定性测试结果如图6所示。由图6结果可知,本文方法比其他2种方法稳定性具有显著优势，采用本文方法对光通信传感器自动控制参数方面的平均稳定性超过95%，比遗传算法、传统粒子群算法控制平均稳定性高，因此本文方法对光通信传感器控制具有较高的稳定性。

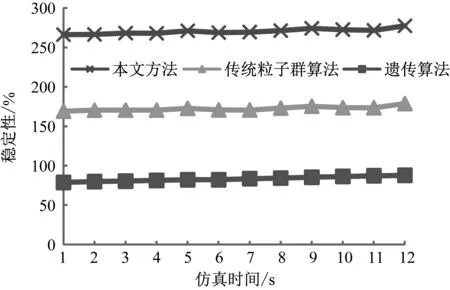
图6 不同方法的稳定性测试

3 总结

为了提高光通信传感器自动控制效率，提出基于人工智能技术的光通信传感器自动控制方法，引入改进粒子群优化算法对光通信传感器自动控制参数实施控制，实验结果表明,本文方法对光通信传感器参数实施实时调整，提高光通信传感器的精度及稳定性，具有十分广泛的应用前景。