高斯过程机器学习在临河地铁车站基坑变形预测中的应用

夏宏运

(中铁第一勘察设计院集团有限公司，陕西西安 710043)

日益拥挤的城市空间给城市轨道交通建设带来了诸多的挑战。临近河道的基坑在开挖施工时，易发生不利的变形影响，能导致河堤结构发生安全风险，引发较大的安全事故。

为保证临近河道基坑工程施工的安全、顺利进行，需选择合理的基坑支护设计方案，如需对周边影响较小的地下连续墙[1]，钻孔灌注桩[2]、SMW工法桩[3]等围护结构，采取隔水措施，防止因水土流失导致结构的安全破坏。

基坑施工过程中需加强施工监测管理，减少因施工基坑导致的因周边既有构筑物变形过大而引发的安全事故。既有构筑物健康监测与变形预测可帮助施工者及时了解施工安全状况，提前规避风险[4]。通常情况下，监测数据能在一定程度上指导基坑安全施工，但其无法有效预测基坑及周边环境的变形规律。合理的监测数据分析方法能有效揭示变形的发展规律。保证基坑施工安全进行的人工智能预测监测变形数据方法是目前较为热门的研究领域，该方法以既有的监测数据作为学习对象，预测变形发展趋势，在实际工程中可有效把控安全风险，并指导工程实践[5]。

目前国内外常用的机器学习方法主要有人工神经网络、支持向量机、高斯过程等。李彦杰等[6]基于遗传算法优化的BP 神经网络建立基坑变形预测模型，渠孟飞等[7]利用支持向量机对基坑变形数据进行预测时指出,不断加入最新监测数据可以取得更好的预测精度。高斯过程相对于人工神经网络的多样本问题，以及支持向量机的超训练问题，是一种较适合岩土结构分析的机器学习方法[8]，其对于处理高维数、小样本、非线性等复杂问题具有良好的适用性[9]，但其核函数的单一性对于特定函数存在学习时拟合效果欠佳等问题。

为解决该类问题，本文拟对高斯过程机器学习进行改良，获取一种改良后的高斯过程机器学习协方差函数，并通过对基坑及河道堤岸的变形监测位移样本点进行训练，获取下一步工序预测变形值，实现对河道堤岸结构的风险预测。

1 高斯过程回归预测

1.1 传统高斯过程方法

基坑的变形由第一步开挖开始形成，并快速发展，直至随着开挖的进行趋于稳定。传统的高斯过程根据对基坑开挖过程的变形监测数据进行机器学习，进而完成预测。

高斯过程回归分析是通过给定一组学习样本，利用贝叶斯理论对该学习样本进行训练并学习，学习样本集可作为其训练样本集基础，然后通过训练得到一组映射关系，当输入一个新的样本后，由映射关系得出的输出值，即为新样本的预测值，该训练集即为样本集的回归分析。

例如：将基坑开挖过程中n个位移的监测值作为训练样本，将开挖一段时间后的位移值作为目标函数。GPR模型就是指通过对训练样本集进行学习并训练，得出相应的函数关系，待输入新的样本x*时，得到目标函数值y*。

GPR模型主要采用以下核函数。

1)平方指数协方差函数(squared exponential covariance function，简写SE)。

(1)

(2)

(3)

2)马特恩协方差函数(matern covariance function，简写MC)。

(4)

(5)

(6)

(7)

(8)

(9)

3)线性协方差函数(linear covariance function，简写LIN)。

(10)

(11)

(12)

式中：l，σf，σn为超参数；l表示各向同性的距离尺度，其个数与变量的维数相等；σf表示局部相关性的程度[10]。

1.2 改良高斯过程回归方法

GPR模型在训练过程中，其训练样本与模型存在一定差异，差异范围区间即置信区间，根据区域宽窄确定置信度，根据置信度可判断是否训练成功，当置信度较大时，置信区间较窄，训练效果好，则训练成功。训练样本点与训练函数的偏差为期望损失值，期望损失值由模型偏差与噪音值组成。

针对不同的训练函数，其模拟效果往往存在较大的差异，训练后可根据训练效果进行比选，根据真实吻合度确定合适的函数。

本次训练学习选用平方指数协方差函数、马特恩协方差函数、线性协方差函数进行训练，同时对比人工神经网络训练，并根据平方指数协方差函数、马特恩协方差函数、线性协方差函数模拟后的噪音计算修正权重ω，当训练置信度不满足成功标准，则权重ω为0，根据权重分配平方指数协方差函数、马特恩协方差函数、线性协方差函数的比重，如式(14)和式(15)所示，获取改良协方差函数的高斯过程回归模型。

根据改良协方差函数与SE，MC，LIN及人工神经网络进行对比，以式(13)sinc函数进行验证，在x∈[-12,12]区间范围内的曲线上随机取48个数据点作为训练样本。

(13)

(14)

y=ωSEfSE(xSE)+ωMCfMC(xMC) +ωLINfLIN(xLIN)。

(15)

以上不同函数的回归模拟效果如图1所示，平方指数协方差函数训练效果较好，马特恩协方差函数效果次之，其峰值概率吻合度高，峰值外吻合度低，线性协方差函数训练效果取决于样本集的分布，当分布较好时，其训练效果较好，当分布具有局限性时，其效果亦存在一定的局限，人工神经网络存在过度训练问题，对样本集的依赖程度最大，根据噪声计算修正权重的协方差函数模拟效果最佳。

图1 不同函数回归模拟结果

高斯过程回归核函数可根据平方指数协方差函数、马特恩协方差函数、线性协方差函数综合训练效果确定。即，采用高斯过程对训练样本进行训练，对训练后的高斯过程回归模型的训练样本进行自回归，获取其置信度，识别训练是否成功，成功则获取其噪声值，根据噪声值计算分配权重，获取最优自适应函数，具体如图2所示。

图2 高斯过程回归协方差函数

以修正协方差函数作为高斯过程回归模型即为GPR代理模型，该代理模型可近似看作样本点(各测点变形)的发展规律，即y=f(X)，对于基坑开挖后续的发展变形可通过函数进行计算，即y*=f(X*)，计算值即为所求取的变形值。

2 工程实例

2.1 工程概况

天津地铁7号线王兰庄站位于卫津南路与规划宝通道交口，沿卫津南路南北向布置，车站西侧附属为D1，D2号出入口，该出入口紧邻津港运河，基坑最深处约10.2 m。

因D1，D2出入口离津港运河较近，基坑围护采用SMW工法桩+内支撑的支护形式，紧邻河道一侧采取SMW工法桩型钢密插措施，竖向设置3道支撑，其中第1道支撑采用混凝土支撑，第2，3道支撑采用钢支撑，剖面关系如图3所示。

图3 出入口与津港运河剖面位置关系图

2.2 工程地质及水文条件

根据详勘报告揭示，该出入口基坑土层属中软土，土层自上而下依次为①素填土，②粉质黏土，③粉质黏土，④粉质黏土，⑤粉质黏土，⑥-1粉土，⑥-2粉质黏土，⑥-3粉土，⑦-1粉质黏土，⑦-2粉砂，⑦-3黏土，⑨-1粉质黏土，主要地质参数如图4所示。

图4 工程地质参数图

2.3 基坑及环境监测

为预测开挖过程中基坑及津港运河的变形变化规律，人工智能机器需要训练既有的变形监测数据以获得变形发展规律函数，并预测变形规律。

在本基坑开挖施工过程中对围护结构顶水平位移、坑底隆起、津港运河河道的坡脚沉降等必测项目进行监测，可直观反映基坑及周边环境的安全状况，减少因基坑施工对周边环境的影响，确保基坑及津港运河的河道安全。

本次监测选取出入口通道中心线所对应的断面作为测点，其中KDC为坑底隆起测点，SQS为围护结构顶水平位移测点，HDC河道坡脚沉降测点。

取3个出入口监测断面，分别对出入口中心位置的KDC59，SQS43，HDC88，以及两侧距离中心15 m位置的KDC60，KDC61，SQS45，SQS46，HDC89，HDC91测点进行监测，基坑开挖施工过程中对监测数据进行收集，具体如图5—图7所示。

图5 坑底隆起变形位移

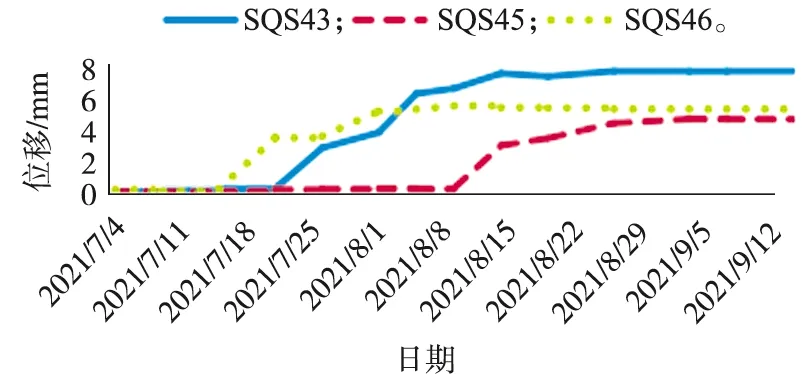
图6 围护结构顶水平位移

图7 运河坡脚沉降位移

2.4 变形预测

基坑开挖过程中往往以有限元计算方法对基坑风险进行评估，该评估依据地质勘察岩土参数进行计算，为验证高斯过程机器学习方法的可行性，拟针对基坑的开挖先利用有限差分软件进行岩土计算，将其结果与改良高斯过程学习预测值进行比较。

2.4.1 有限元预测

津港运河的安全主要受控于周边的地层变形与扰动，根据施工过程中的工况进行模拟分析，结构计算模型如图8所示，主要分别对如下工况进行模拟。

图8 结构计算模型

工况1：模拟基坑的围护结构施工，并初始化地应力。

工况2：土层开挖至冠梁顶以下1.3 m，架设第1道支撑。

工况3：土层开挖至冠梁顶以下5.3 m，架设第2道支撑。

工况4：土层开挖至冠梁顶以下8.7 m，架设第3道支撑，并开挖至坑底。

有限元预测选取基坑的最不利开挖面进行计算。

模型采用的M-C弹塑性模型在数值计算中效果较好[11]，本次有限元计算假定土层为简单的均质分布的弹塑性材料。

计算模型采用传统的四周实施水平约束，底部实施竖向约束，顶面不施加约束。

模型的取值范围为100 m×60 m×60 m(长×宽×高)，在此区域模拟土层。整个三维有限元计算模型共45 176个单元，57 785个结构节点。

施工过程中部分基坑开挖，围护结构的侧向土体发生挤压，导致土体发生变形，其中土体最大的水平位移为1 mm，坑底最大隆起为3.8 mm。津港运河的变形以发生整体沉降为主，最大沉降值为1.5 mm。具体变形如图9—图11所示。

图9 第1步开挖变形位移图

图10 第2步开挖变形位移图

图11 第3步开挖变形位移图

2.4.2 改良高斯过程回归预测

采用改良高斯过程回归模型进行预测，并与传统高斯过程回归方法所得结果进行比较；训练样本点采用监测数据，监测数据的数量对于训练的效果有直接影响[12-13]。

本次以D1，D2出入口作为研究对象，以第1步开挖、第2步开挖、第3步开挖计算变形为目标函数值，并以基本参数(基坑长、宽、深度、基坑暴露时间)为样本点变量，采用python语句调用高斯过程回归机器学习语句为工具[14]，对以上数据进行训练，并预测基坑开挖至坑底时的变形量。

高斯过程回归函数可通过对多个样本点进行函数训练，该函数为高斯过程回归隐式函数，训练样本集主要由开挖深度(第1步为1.3～5.8 m，第2步5.8～8.7 m，第3步8.7～11.2 m)之间的0.1 m的精度确定训练样本，除基坑开挖过程中实测的样本外，其他均以差值法生成。例如，结合表1所示，第1步开挖深1.3 m至第2步开挖深5.8 m，其学习样本为X1=(1.3，1.4，1.5，…，5.8)，坑底隆起Y1=(2.96，2.98，3.00，…，3.78)，共46个学习样本；第2步开挖深5.8 m至第3步开挖深8.7 m，其学习样本为X2=(5.8，5.9，6.0，…，8.7)，坑底隆起Y2=(3.78，3.79，3.80，…，4.01)，共30个学习样本；第3步开挖深8.7 m至第4步开挖深11.2 m，其学习样本为X3=(8.7，8.8，8.9，…，11.2)，坑底隆起Y3=(4.01，4.03，4.05，…，4.51)，共26个学习样本。第1次拟合训练样本为(X1，Y1)，第2次拟合训练样本为(X1，X2，Y1，Y2)，第3次拟合训练样本为(X1，X2，X3，Y1，Y2，Y3)。本次预测针对坑底隆起位移、围护结构顶水平位移、运河坡脚沉降位移三次函数进行训练，拟建立3个隐式函数。3个函数均以开挖深度、基坑的变形位置、开挖工序作为其求解变量矩阵[15]，以变形位移作为其目标值，进行高斯过程机器学习函数的训练[16]，将训练后的函数再次代入预测对象进行预测，具体流程如图12所示。

图12 高斯过程回归预测流程图

本次改良高斯过程在训练的基础上不断拟合并验证方法的可行性，同时动态更新训练样本。为验证本方法的可行性，研究分3步进行拟合：第1次，基坑施工开始至开挖至第2道支撑下0.5 m；第2次，基坑施工开始至第3道支撑下0.5 m；第3次，基坑施工开始至开挖至底。

由于高斯回归预测方法需要将施工过程收集的变形位移监测数据作为学习样本[17]，因此从第2步基坑开挖至第2道支撑下0.5 m开始进行变形预测，并着重对高斯过程机器学习样本最多的时刻(即开挖至坑底时)的变形进行预测。

针对三步开挖的变量较少的问题，人为用差值法设置多个样本，根据差值法确定,本次训练分别运行50次，并根据不同结果取平均值。

为了验证改良高斯回归预测方法的优越性，笔者将其与有限元法计算值、传统高斯预测值和实测值进行比较[18]，结果详见表1。

表1 预测值比较

由表1可知：因训练样本较少，学习训练效果差，第2步开挖结束时的训练效果容易失真，不能有效地预测基坑的变形，第3步的预测值基本可信，开挖至坑底时的训练效果最佳。同时，改良高斯过程回归函数预测的变形位移值较有限差分计算软件的计算值更吻合实测值，从开挖至坑底时的数据可知，坑底隆起量与实测值的准确率为98%，围护结构顶水平位移与实测值的准确率为98%，运河坡脚沉降与实测值的准确率为95.3%，其优于有限元法预测所得计算值的准确率(91%，71.8%和94%)，也优于传统的高斯过程学习方法的准确率(98%，97.5%，95.2%)。

综上所述，改良高斯过程回归机器学习的预测方法可应用于工程监测数据预测分析，在工程应用中能快速地对已有的变形进行训练，并对可能出现的险情进行预测，帮助施工方制定应急预案，并提前做好准备，保证施工的安全进行[19]。

3 结 论

本文以天津地铁7号线王兰庄站出入口临河基坑工程为例，将基坑开挖过程中的变形位移监测数据作为学习样本，利用改良高斯过程机器学习对样本进行训练，预测基坑变形位移[20]；并与有限元预测结果及传统高斯过程回归预测结果进行了对比，得出以下主要结论：

1)以常用的高斯过程核函数为基础，引进权重分配的方式获取改良高斯过程回归代理模型，通过数学函数进行验证，该改进高斯过程回归函数比平方指数协方差、马特恩协方差、线性协方差、人工神经网络等常用函数的可信度更高，训练结果吻合效果更好；

2)提出的改良高斯过程机器学习预测基坑变形方法较传统有限元评估方法和常规高斯过程学习方法，其预测结果更准确，可为后续施工提供安全指导。

改良高斯过程机器学习模拟在样本点不足的情况下，依然存在变形预测值易失真的问题。因此，如何提高该方法处理小样本问题时的分析和预测能力是今后研究的重点。