基于积木式传递矩阵法双转子系统临界转速计算

都昌兵，邱清竣，舒 毅

（长沙航空职业技术学院，湖南 长沙 410124）

带轴间轴承的双转子系统是航空发动机的典型结构。航空发动机的使用经验表明：在某些转速下，转子的挠度显著增大，同时出现较大的不平衡力和力矩，这些转速称为临界转速。如果发动机在临界转速附近工作，其振动大大加剧。转子在远小于或大于临界转速下运转时，其工作平稳，挠度很小[1]。临界转速现象是转子系统的固有特性。对于单转子系统来说，临界转速的数值由系统结构决定，而与工作转速无关。但是，对于双转子系统来说，在不同转速比下，由于轴间轴承的影响，系统特性（转子相互作用、耦合作用的强弱不同）有所改变，将对临界转速产生影响。

1 积木式传递矩阵的基本原理

积木式传递矩阵是一种用于计算单、双转子系统临界转速的理想方法。任何复杂的转子均可由若干“标准”类型的转子大段（简称：积木块）组合而成，积木块的右端为转子始端或轴承结合面的左侧，其左端为转子的末端或轴承结合面的右侧。对每类积木块分别编制了由其右端状态变量来计算其左端状态变量的标准程序。当要计算实际转子的临界转速时，只要将相应的积木块程序调用搭接即可[2]，而不需要重新编制源程序。

2 航空发动机典型构件的传递矩阵

2.1 带弹性支承的刚性薄圆盘

对于带弹性支承的刚性薄圆盘，设第j个支承的总刚度为Ksj，其传递矩阵为：

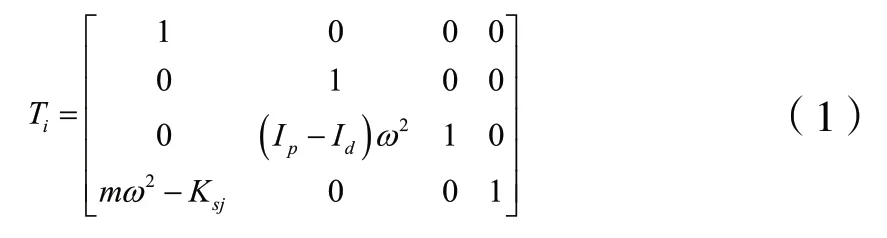
式中：Ip、Id分别为单元直径转动惯量、单元极转动惯量，m为刚性圆盘集质量，ω为转速。

2.2 无质量等截面的弹性轴段

无质量等截面的弹性轴段的传递矩阵为：

式中：l为轴段的质量，E为材料的弹性模量；J为轴段的截面距；γ为考虑剪切影响的系数。

2.3 圆盘和轴段的组合件

圆盘和轴段的组合件的传递矩阵为：

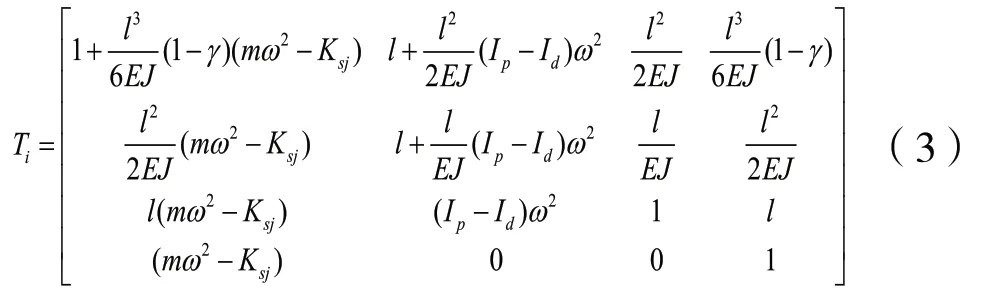
2.4 点质量

点质量的传递矩阵为：

3 双转子系统临界转速的计算

3.1 双转子模拟实验器

双转子模拟实验器结构如图1所示，由内、外两个转子组成，其中：内转子支承形式为1-2-1，外转子支承形式为1-0-1，外转子的后端采用了轴间轴承。

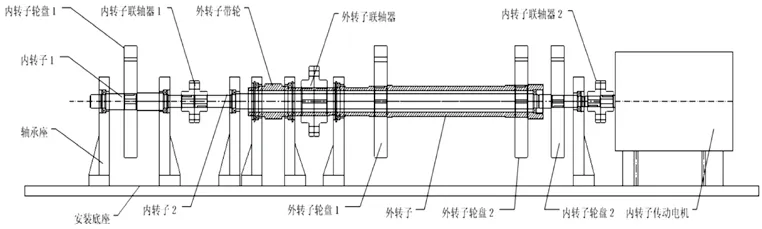
图1 双转子模拟实验器结构图

3.2 计算模型的建立

根据双转子模拟实验器的几何、物理参数来建立转子的传递矩阵理论计算模型。

（1）转子系统的分段

根据支承、联轴器的位置，把内、外转子分为几个大段；在各大段内根据轴的特点分站。为了便于计算，内、外转子统一分段，即内、外转子的分段数相同，相对应段的截面数也相同。由于外转子比内转子短，故在外转子两端添加质量、长度为零的虚拟段，使其和内转子段数相同。其中KB表示内转子的大段号，KA表示外转子的大段号。分段的结果如图2所示。

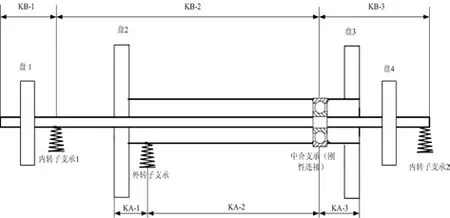
图2 双转子系统简化模型

内转子之间通过柔性联轴器连接，为了便于计算，从联轴器处把内转子分成两部分。建立模型时，选取右侧的轴段。

（2）轴的处理

根据轴径以及轴上安装零件的不同，将轴分成若干等截面的轴段，段数分得越多，计算结果越准确，但计算量也越大。凡是轮盘、轴承位置、轴径（外径或内径）和材料有变化的位置，都选作分段截面。对于等截面的轴段过长的段，则将其分成若干小段。

轴的质量按集中质量处理。轴的质量简化成有限个集中质量，各轴段的质量按质心位置不变的原则分配在各轴段的两端面上。

（3）轮盘的处理

轮盘简化为集中质量（位于轮盘重心截面的轴线上），但考虑其直径转动惯量和极转动惯量[3]。

（4）支承条件的简化

将支承系统简化为弹性支座。支承系统的刚度，根据试验或计算确定。支承的刚性系数按以下的经验公式计算：

①同时受径向和轴向载荷的滚珠轴承的柔性系数[4]：

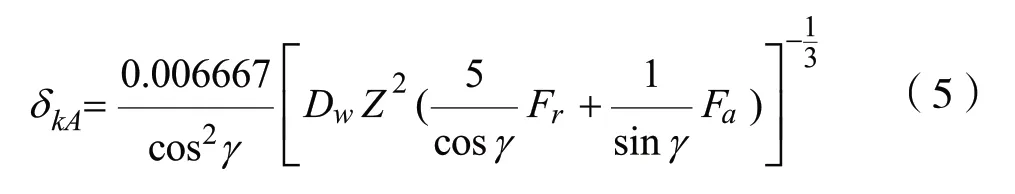
②只受径向载荷的滚珠轴承的柔性系数：

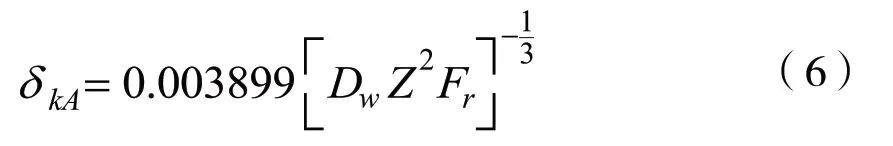
式中：

γ-滚珠与轴承外环的接触角；Dw-滚珠直径；

Fγ-径向载荷；Fa-轴向载荷；Z-滚珠数量。

本文中的支承均按照弹性支承来进行处理。

（5）计算模型

按照轴分段的结果，再把每段轴分为若干个节点，经过简化的计算模型如图3所示。

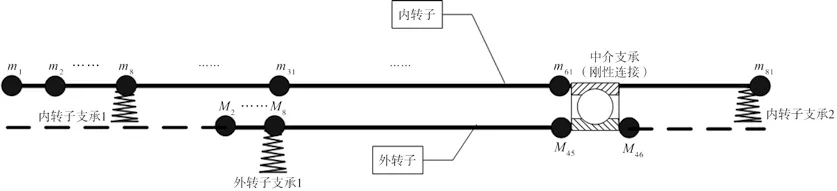
图3 双转子系统计算模型

（6）编制数据文件

根据理论计算模型，编制数据文件。

数据文件的格式是一个18×N阶的输入矩阵。N指的是轴划分的截面数。矩阵的各行元素为该截面的内外转子的几何、物理特性，如轴的长度，轴段的内径和外径，轴的支承条件，有无盘、联轴器等附件，有无附加的质量等，作为选取计算模块的依据，以及计算参数数值[5]。

3.3 边界条件

双转子模拟实验器中，外转子的一端为悬臂端，另一端通过柔性联轴器、传动带与电机相连，在理论计算模型中按自由端来处理。内转子的一端通过柔性联轴器与电机相连，另一端为外伸的自由端，计算时按两端都是自由端处理。

3.4 程序流程图

在计算内转子临界转速时，先将外转子固定在某一个转速下，然后用频率扫描法计算内转子的临界转速。改变外转子的转速，重新计算在新的外转子转速影响下的内转子的临界转速。这样就可以得出在不同的外转子转速之下的内转子的临界转速。计算的程序流程图如图4所示。

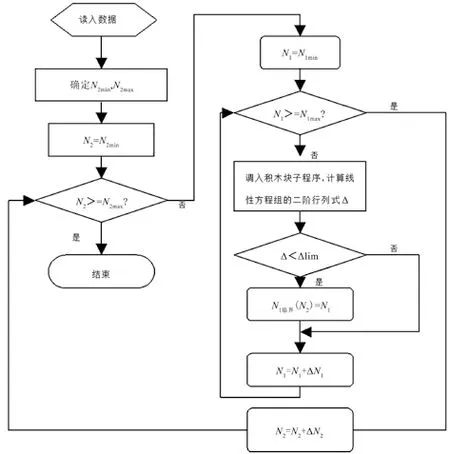
图4 临界转速计算流程图

外转子的临界转速计算方法与内转子的临界转速计算方法相同，即计算在不同的内转子转速影响之下的外转子的临界转速。它的程序流程图不再给出。

4.计算结果与分析

4.1 内转子的临界转速计算结果

先给定外转子的一个转速，求解在该转速下内转子的临界转速值；再改变外转子的转速值，计算外转子在另一个转速下时内转子的临界转速值；重复以上的计算，即可求得外转子在各个转速时内转子的临界转速值；根据计算结果，绘制出内转子的临界转速随外转子转速变化的曲线，进而分析其变化规律。

（1）内转子的一阶临界转速随外转子转速的变化

表1给出了在不同的外转子转速下的内转子的一阶临界转速的计算值。

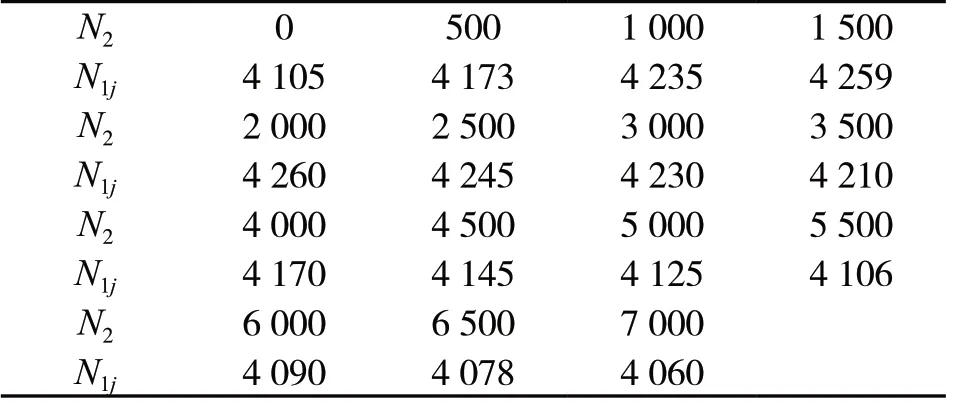
表1 内转子的一阶临界转速（单位：r/min）

内转子一阶临界转速随外转子转速的变化规律如图5所示。

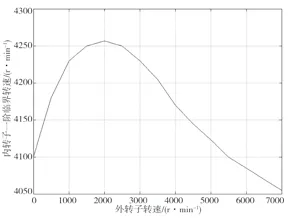
图5 内转子一阶临界转速随外转子转速的变化

从表1、图5可以看出：当外转子的转速在0～7 000 r/min变化时，随着外转子转速的增加，内转子的一阶临界转速先增加、后降低；在外转子转速值为2 000 r/min时，内转子的一阶临界转速达到最大。说明：转子系统运转过程中临界转速是变化的，变化的原因是外转子转速的变化导致了内转子在中介支承处的动刚度发生了变化。动刚度的增加导致了内转子临界转速的上升，动刚度的降低会导致临界转速的下降。

（2）内转子的二阶临界转速随外转子转速的变化

表2给出了在不同的外转子转速下的内转子二阶临界转速的计算值。

内转子二阶临界转速值的变化规律如图6所示。

从表2、图6可以看出，随着外转子转速的上升，内转子的二阶临界转速值上升，并且上升的幅度逐渐减小。其原因是外转子转速的上升导致了内转子支承的动刚度增加，使得内转子的二阶临界转速上升。

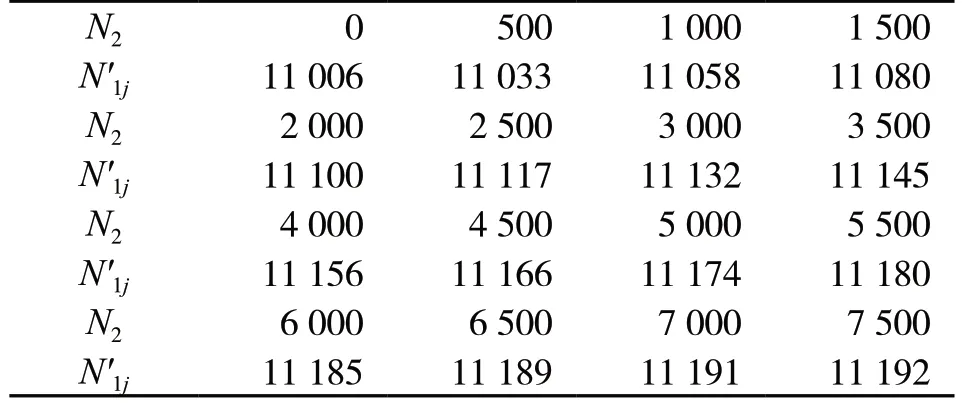
表2 内转子的二阶临界转速（单位：r/min）

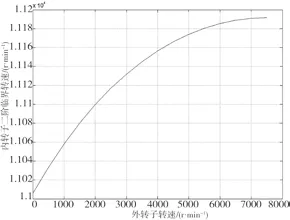
图6 内转子二阶临界转速随外转子转速的变化

4.2 外转子临界转速的计算结果

表3给出了在不同的内转子转速下的外转子一阶临界转速的计算值。

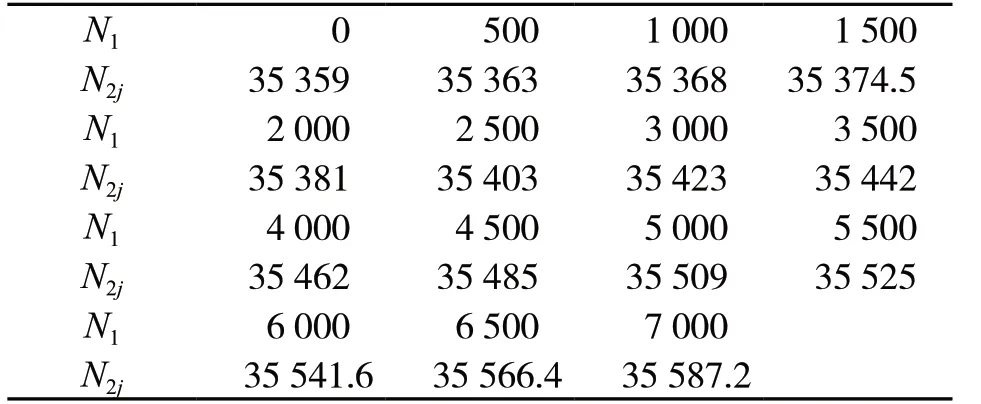
表3 外转子的一阶临界转速（单位：r/min）

外转子一阶临界转速随内转子转速变化的规律如图7所示。

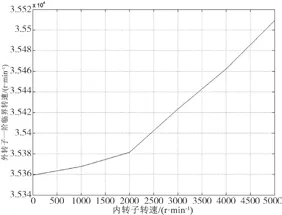
图7 外转子的一阶转速随内转子转速的变化

从表3、图7可以看出，外转子的一阶临界转速随内转子转速的上升而上升。原因是随着内转子转速的增加，外转子和中介轴承相连接的部分动刚度增大，导致了外转子的一阶临界转速的上升。

4.3 临界转速的振型

在求得了临界转速值以后，就可以利用前面的计算结果求解转子在临界转速下的振型，即转子的挠曲线。求解的方法是先假设初始段的状态变量，由于初始段是自由端，所以在位移Χi、挠角θi、弯矩Mi和剪力Qi中，弯矩Mi和剪力Qi为零，设位移Χi为1。

内转子过一阶临界转速，而外转子在一阶临界转速以下时，内外转子的挠曲线如图8所示。

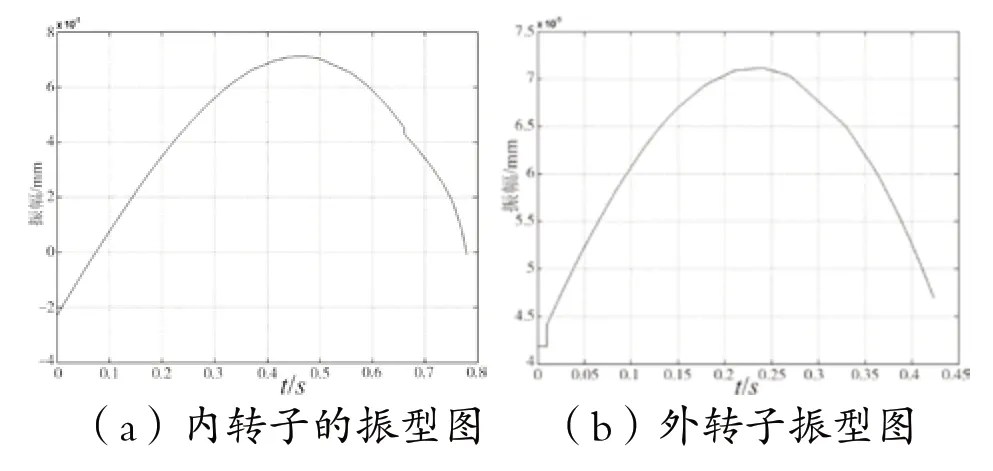
图8 内转子过一阶临界转速时内外转子的振型（N1=4 500 r/min ，N2=1 000 r/min）

内转子过二阶临界转速，而外转子在一阶临界转速以下时，内外转子的振型如图9所示。

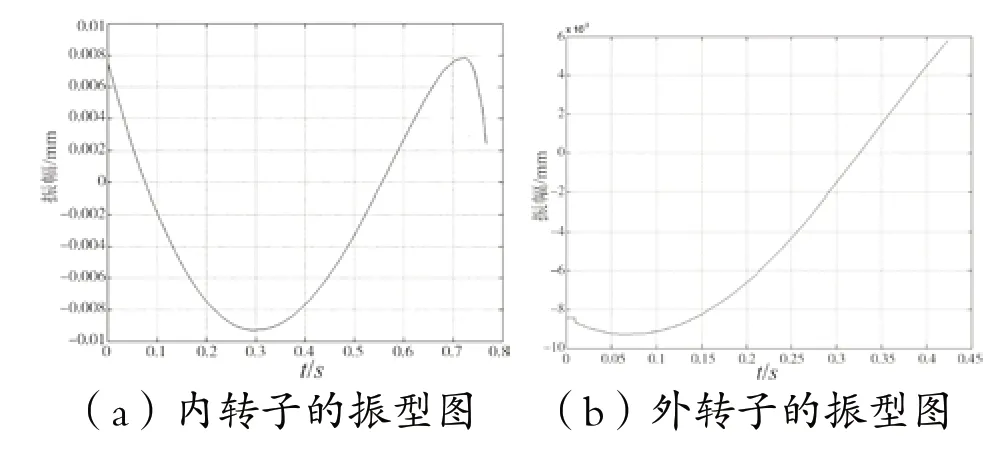
图9 内转子过二阶临界转速时内外转子的振型（N1=12 000 r/min，N2=1 000 r/min）

内转子在一阶临界转速以下，而外转子在一阶临界转速以上时，内外转子的振型如图10所示。

图10 外转子过一阶临界转速时内外转子的振型（N1=1 000 r/min，N2=35 000 r/min）

5.结论

（1）计算发现转速对临界转速值的影响规律：内转子的一阶临界转速随着外转子转速的上升先上升、后下降，二阶临界转速随着外转子的转速增加而不断增加。外转子的一阶临界转速随着内转子转速的增加而增加。

（2）在振型方面，内转子的振型随着内转子转速的不断上升而发生变化，它的相应阶的振型与弯曲振动时各阶振动的振型基本形同。

（3）对于实际的航空发动机来说，由于高低压转子之间存在着一定的转速差，因此它的转速比在一个比较窄的范围内变化，而不是任意的。在处理这一问题时，可以把内外转子的转速变化曲线画到双转子系统的临界转速图谱中，转速曲线和临界转速曲线的交点就是实际各阶的临界转速。