摇摆工况下电动汽车高速斜齿轮传动振动控制方法

戴良朋，李 强，邹来平

(1.杭州超凡汽车维修服务有限公司，浙江 杭州 310004；2.浙江省特种设备科学研究院，浙江 杭州 310000)

0 引言

电动汽车作为人类的重要代步工具，已经融入到现代社会的生活、工作等各领域中，应用范围越来越广、生产量也越来越大。然而由于电动汽车属于消耗品，随着使用频次的增加，内部零件不可避免会出现老化，其齿轮、轴承或其他零件发生松动损坏，导致高速运作时出现振动干扰。斜齿轮的传动振动不仅会缩短电动汽车的使用寿命、影响稳定性，如果不及时进行检修还会出现事故，使生命及财产安全受到威胁。基于此，需要一种针对性的控制方案，解决电动汽车高速斜齿轮产生的强震问题。

由于摇摆工况下高速斜齿轮传动有很多非线性因素(如非线性湍流、非线性间隙和非线性时变等)，这些因素会增加传动的不可控性，导致出现混沌振动现象，对正常齿轮工作的稳定性及可靠性产生较大影响。本文采用混沌控制方式控制高速斜齿轮转动振动，在控制前分析了振动因素特性及混沌参数的形成过程，利用反共振频率对噪声数据进行识别，采用线性反馈控制方法调控自由度数值，改变斜齿轮传动的振动频率，使得高速运动稳定到规律性的周期轨道上。不仅解决了震颤影响，还通过噪声识别降低了外界干扰因素的输入，提高控制质量及效率。

1 电动汽车高速斜齿轮传动振动产生因素分析

本文着重研究斜齿轮传动点处振动产生原因。明确说明传动点的功率特性，帮助后续控制能更明确具体方向，减少误判率，提高控制效果。

导致电动汽车高速斜齿轮传动振动的原因主要有2点：一是因为发生振动时传动的速度比[1]大小不变，但斜齿轮金属带内的功率流向发生变化，此时，汽车的齿轮转动系统正从无级变速[2]转换为传动变速，由于速度的不统一，导致齿轮扭矩的方向大小都出现了偏移，进而产生震颤影响；二是因为在传动点处，离合器L3(如图1所示)的主转速和从转速[3]不一致，此时，离合器L3又需要尽快接合，必然会出现冲击振动。

图1 混合无级变速传动

综合上述分析，导致电动汽车高速斜齿轮传动振动的主要原因是，摇摆工况造成的无级变速无法顺利转换，因此主要分析无级变速的影响因素。

无级变速在转换时，无级变速器(continuously variable transmission，CVT)传动装置的速度比δt与金属带速度比δ成反比关系。当处于纯无级变速时，二者比值则会变为正比，会随速度的增大而增大，此时δ=δ-δt，描述公式为

(1)

a为斜齿轮参数；δc为斜齿轮速度比。

计算正反关系下速度比的变化率dδt/dt，公式为

(2)

t为时间系数；v为汽车行驶速度；r2为轮胎半径；δf为传动速度比；n为发动机转速；θ为油门的开合度[4]。统计整理这些参数之间的正向关系，可得到摇摆工况下电动汽车高速斜齿轮传动的副参数[5]，以及在最高转速、额定转速以及最大转矩3种情况下的工况参数[6]。

2 斜齿轮传动振动噪声参数识别方法

在分析电动汽车高速斜齿轮传动振动产生因素的基础上，识别斜齿轮传动振动噪声参数。电的导纳是动力学系统中一项重要物理量化[7]，用于描述系统内力学信号的响应情况，可用来表示傅里叶变换与激励傅里叶变换后的比值，该比值参数为：速度导纳、位移导纳以及加速度导纳。根据傅里叶变换规律可得到参数之间的关系为：

(3)

(4)

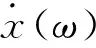
斜齿轮在无阻尼[11]约束的情况下，传动振动二自由度的系统的质量点[12]为m1，该点及原传动点处位移导纳计算公式为：

(5)

(6)

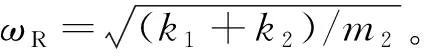
根据上述参数关系可推导得出：

(7)

(8)

(9)

(10)

ke为质量点实际值。当存在已知的高速斜齿轮传动原点时，可根据式(7)～式(10)计算识别出的物理控制参数，帮助后续控制算法的理解与判定。表1准确统计了动力学物理参数识别值与理论值间的差异性，结果证明了本文识别方法获得的识别结果是精准的。

表1 二自由度系统物理参数识别值与理论值对比

3 基于混沌控制的斜齿轮传动振动控制方法

将摇摆工况下电动汽车高速斜齿轮传动，定义为一种n维表达系统为

(11)

设该力学斜齿轮传动系统的线性反馈控制公式为

W=G(y1-y2)

(12)

G为反馈数据增益矩阵[15]。

假设G=[g,0]T，g为反馈控制调节系数，此时系统的传动振动输出值就为x，最终的振动控制方程为

(13)

由此推导，就可以将电动汽车斜齿轮传动时产生的振动，控制在稳定的周围运动轨道上，在实际运行时可利用传感器装置，通过现场情况对应调节振动角度及反馈系数g，使得系统逐渐趋于稳定状态。

4 仿真测试

4.1 测试设置

设摇摆工况下电动汽车高速斜齿轮传动振动波频长度为64 Hz、步长为0.05、矢量叠加噪声信号方差为0.000 5 dB。设定仿真测试的控制负载量为1 N·m，采用调整电动汽车驱动机的方式来调整斜齿轮的转速，测试在200 Hz及400 Hz转速频率下本文方法的主动控制效果。

完成上述步骤后，利用Mathworks公司推出的Simulink建立模块图环境，帮助多域仿真及模型设计。仿真测试将以2部分进行：一是针对传动振动加速度以及斜齿轮啮合处的振动频率，检测方法的整体控制效果；二是测试在单一转速下，分析本文控制方法对输出电压的控制效果。因为不稳定的输出电压会影响斜齿轮的啮合度，导致传动振频增大，所以检测输出电压的控制效果，也是测试优异程度的重要标准之一。

4.2 基于传动振动加速度及啮合处振动频率控制效果

根据传动振动加速度及斜齿轮啮合处的变化特性，分别用信号频谱及瀑布图来表示最终的控制结果，测试结果如图2和图3所示。

图2 控制前后振动加速度信号的频谱

由图2可知，随着斜齿轮运动转速的不断增长，由于频率带动的影响，传动振动的加速度也在随之不断上升。从图2中的对比点可以明显看出，当斜齿轮传动频率为324 r/min时，控制前与控制后的振动加速度从原始的-34 dB衰减到-62 dB，控制效果较为明显。

从图3a中可以看出，控制前斜齿轮啮合部分的传动频率整体变化较为混乱、波动范围过大、频率表达不一致，且振幅及振频的规律性不强、稳态性较差。反观图3b经过本文方法控制后啮合部分的频谱，整体变化幅度缩小，频谱走向逐渐趋于平稳且没有出现过高或过低的大幅度信号，振动频率没有因转速的增加而上涨，这是与内部共振区域频率波动相吻合的表现。这是因为，只有齿轮转轴及啮合部分的振动频率相同，才能保证主转速与从转速的方向及大小都一致，达到稳定运行。由此说明，本文方法对斜齿轮传动振频具有很好抑制效果，且收敛速度较快、控制准度较高，可靠性及适用性较强。

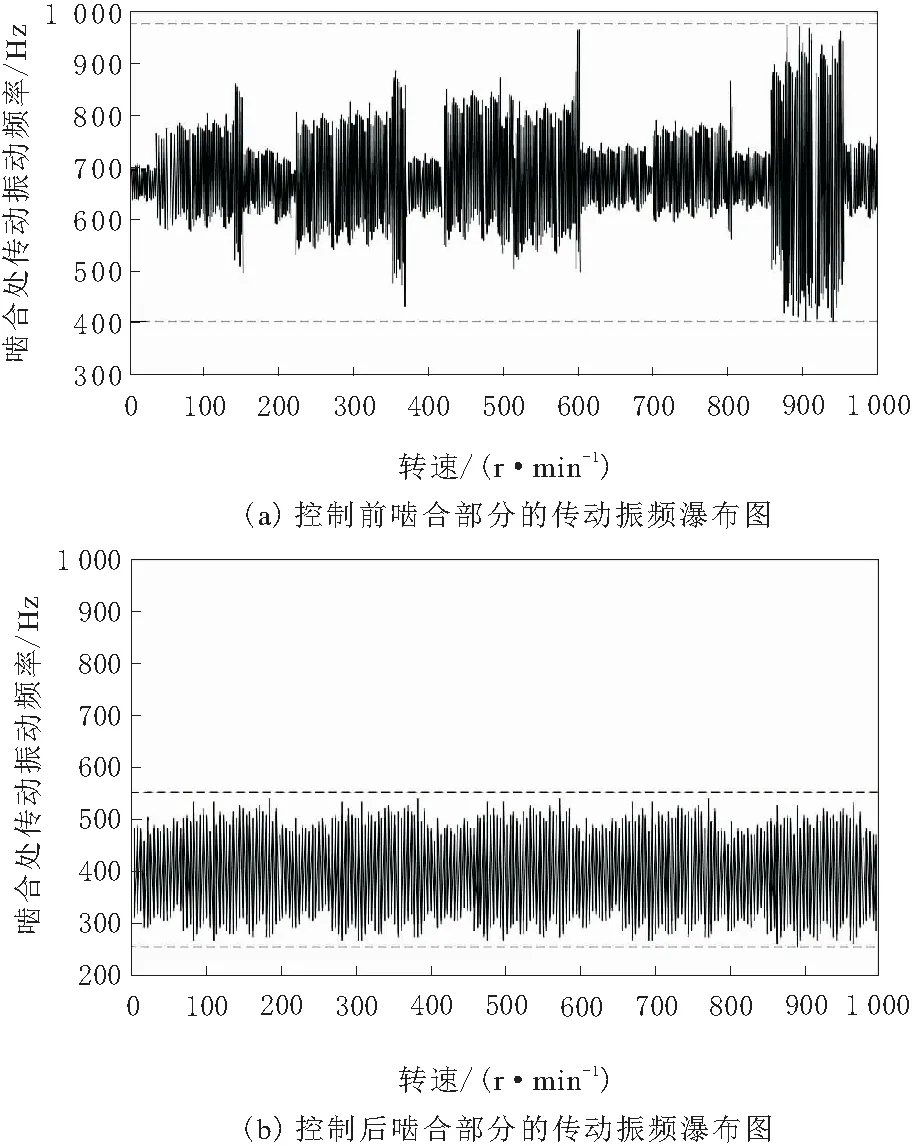
图3 控制前后啮合部分的传动振频瀑布图

4.3 振动输出电压控制结果

选择300 Hz的传动频率作为本次测试的环境，电压控制结果如图4所示。

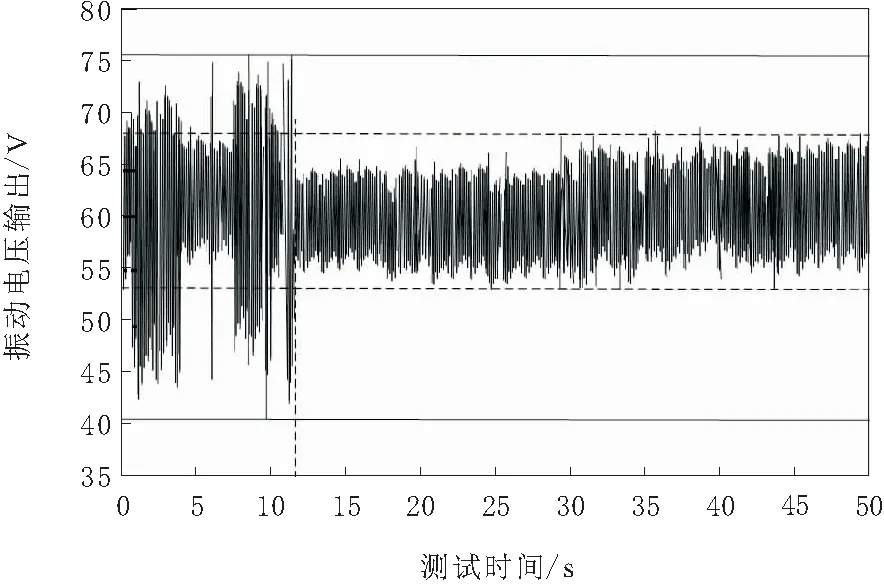
图4 电压源输出电压的控制结果

从图4可以看出，在时域振动加速度控制历程的0～12 s间，输出电压一直处于不稳定的随机波动状态，而在第12 s施加控制后，斜齿轮的电压从原来的76～41 V逐渐衰减至68～54 V，直至50 s的测试时间内一直保持稳定。从控制后电压信号的波形可以明显看出，没有出现大步长导致的带外超调现象，且信号频谱表达的规律性较强，上下波峰基本保持一致。这说明，本文的控制算法具有较好的稳定性及收敛速度，还具有一定的可靠性及实用性，有效解决了振动噪声带来的波频混乱现象，整体控制效果表现优异。

5 结束语

本文以电动汽车高速斜齿轮传动振动产生因素为切入点，得出斜齿轮参数、速度比、行驶速度以及发动机转速之间存在的正比关系。利用傅里叶变换规律推导得出速度导纳、位移导纳以及加速度导纳传动振动的无阻尼自由度系统，该系统可以很好地识别斜齿轮矢量传动点的共振及反共振。采用反馈线性控制法，通过参数调节实现了传动振动的稳定周期性控制。相比于非线性控制，线性控制更具有稳定性、权值波动不大且收敛速度较快，频率特性影响误差较小。仿真测试证明，本文方法的控制效果较好，对输出电压及传动振动频率都有明显的改善，消除了噪声信号引起的振频波动及带外超调问题。