基于CSA-NARX模型的电梯钢丝绳动态张力预测方法

叶杰凯，汤小明，胡建钦，易灿灿

(1.丽水市特种设备检测院，浙江 丽水323000；2.武汉科技大学，湖北 武汉 430081)

0 引言

近年来，越来越多的电梯安全隐患问题被报道出来，乘坐电梯时是否安全成为了热点话题。要探究电梯的安全隐患问题，就以钢丝绳的安全性首当其冲。GB/T 31821《电梯主要部件报废技术条件》和GB/T 10060-2011《电梯安装验收规范》等标准都对电梯钢丝绳的检验方法提出了明确要求。因此，实现对电梯钢丝绳的动态张力进行预测，可以有效防止安全事故的发生。

目前，对电梯钢丝绳张力过大的预防研究，已经朝多元化方向发展。以钢丝绳的直径检测为基础的探伤研究[1-2]可以对电梯安全事故的发生起到一定的预防作用，但是在电梯的实际运行过程中，每一根钢丝绳的受力是不相同的。这样一来，以钢丝绳直径为基础的探伤研究就略显无力。基于电控的钢丝绳张力调节装置[3]在钢丝绳张力不均匀或者张力过大时，可以通过调节丝杠来平均钢丝绳的张力，不足之处在于其调节范围有限，不能满足对钢丝绳安全性的要求。传统的自回归滑动平均模型(auto regressive moving average，ARMA)[4]通过计算拟合出1条最符合历史数据的平滑曲线来对数据进行预测，这种方法较为简便快速，但是对数据的平稳性要求较高，同时误差也比较大。常用的长短期记忆(long short-term memory,LSTM)[5]通过设置一些筛选器来选择忘记训练数据中不重要的部分记住重要的部分，达到提取数据关键信息的效果，从而对数据进行预测[6-7]。但是LSTM模型的参数较多，训练难度很大，响应慢同时容易过拟合[8]。

本文对带有外部输入的非线性自回归神经网络(nonlinear auto-regressive model with exogenous inputs，NARX)[9]进行研究，用于对电梯钢丝绳张力时间序列数据进行预测。NARX是一种闭环训练神经网络，在训练过程中不断地将历史训练结果代入为下一时刻输入的一部分，提高训练结果可靠性，减少误差。为了找到NARX网络中的最佳参数使训练过程更快速，结果更精确，本文结合变色龙算法(chameleon swarm algorithm，CSA)[10]对NARX神经网络模型的延时阶数、隐藏层个数和学习率等关键参数进行优化。最后，本文基于实测的电梯上行过程中单根钢丝绳的张力数据，分别利用上述3种算法(ARMA、 LSTM和 CSA-NARX)对该数据进行预测分析，通过预测精度的指标对比来说明本文所提出模型的有效性。

1 理论与算法

1.1 NARX网络原理

NARX神经网络在训练的过程中会以一定的权重将前几个时刻的数据信息纳入训练，是一种高效且精准的闭环动态神经网络[11]。NARX神经网络通过自身的闭环以及延时结构，能够将前几个时刻的预测结果与前几个时刻的输入数据一起计算，有效地防止了数据部分信息的丢失[12]，大大提高了预测的准确性。在输入层中，NARX网络的目标输出也作为输入部分参与训练，让网络在训练过程中考虑到的权值较多，有利于模型数据的拟合[13]。

图1 NARX闭环神经网络拓扑结构

1.2 NARX神经网络训练算法

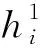
(1)

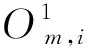
(2)

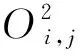
(3)

g为输出层的传递函数。

对于反馈部分来说，所涉及到的误差值δ描述为

(4)

(5)

m=1,2,…,n

(6)

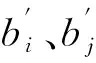
(7)

(8)

设定好模型的迭代次数之后，即可按上述算法进行迭代；判断迭代是否结束，如果结束即得到最终结果，如果没有结束则返回算法开始处再进行迭代。

在NARX神经网络模型中，参数的设置对模型预测精度的影响极大。学习率α，输入数据与输出结果的延时阶数D1、D2，隐藏层神经元个数C1都是影响预测精度的关键参数。延时阶数过大，神经网络模型所计算的权值就会更分散，这就容易导致模型出现过拟合的现象，同时会使计算量急剧上升，致使模型迟钝；延时阶数过小，容易导致神经网络模型欠拟合，影响模型精度。神经元的数量设置得过大，会导致神经网络模型计算缓慢，同时容易过拟合；反之，如果神经元的数量设置得过小，会致使神经网络模型学习效果不佳，拟合不成功。学习率α是大于0的正数，如果设定的学习率数值太小，那么神经网络模型中各参数的起伏会很小，这种情况下学习过程的梯度会下降得很缓慢，学习时间将会被大大延长；如果设定的学习率数值太大，可能会导致误差值δ的极小值无法选取，进而致使整个训练过程是发散的。

1.3 变色龙优化算法

鉴于NARX神经网络在训练过程中，为保证训练效果与精度，需要寻找上述参数的最优值，本文采用变色龙算法对上述参数进行寻优，达到提高NARX神经网络模型训练效果的目的。

变色龙算法主要模拟了变色龙在树木、沙漠和沼泽附近寻找食物时的动态行为。该算法寻找最优解的能力强，得到的最优解误差小，重要的是该算法的寻优速度快。该算法对变色龙寻找食物的行为步骤进行数学建模和实现，其中包括寻找变色龙最佳位置，变色龙的眼睛旋转近360°进行猎物定位，用高速发射的粘性舌头捕获猎物。

a.变色龙搜索猎物。变色龙搜索猎物的方式为

(9)

b.变色龙眼睛的旋转。此阶段通过模拟变色龙眼睛的旋转来锁定猎物时的位置更新，即

(10)

c.变色龙捕获猎物。变色龙的舌头落向猎物的速度定义为

(11)

作为一种元启发式算法，变色龙优化算法与其他算法相比，它提供了有利的全局或接近全局的解决方案和更好的性能。在优化NARX神经网络参数方面，这些参数并不能依靠以往的经验去确定其范围。在这一方面，变色龙优化算法提供了相对于其他优化算法而言更好的解决方案。

1.4 基于CSA-NARX的钢丝绳张力预测模型

本文将变色龙优化算法与NARX神经网络算法相结合，提出一种CSA-NARX优化预测模型。以NARX神经网络模型为训练数据的载体，以变色龙优化算法为NARX神经网络参数优化的载体，以达到更准确、快速的预测效果。CSA-NARX预测模型的流程如图2所示，将采集到的电梯钢丝绳张力数据经过处理后，将其划分为训练数据集和验证数据集。将训练数据集输入经过变色龙优化算法优化参数过后的NARX神经网络模型，并进行预测。通过对比验证数据集，计算预测数据的均方根误差RMSE和回归系数R2，来对CSA-NARX预测模型的精度进行评价。其具体实现过程如下：

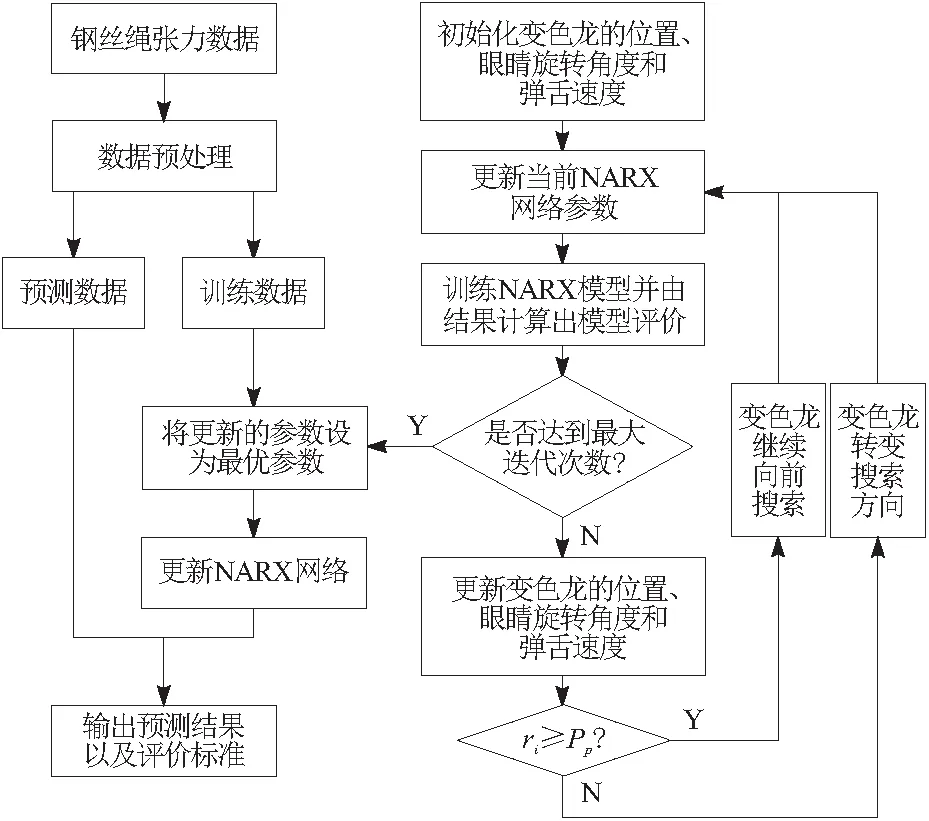
图2 CSA-NARX预测模型流程

a.将采集到的电梯上行时钢丝绳张力的数据经过处理后，划分为训练数据集与验证数据集。

b.初始化NARX神经网络中的关键参数，包括延时阶数、隐藏层神经元个数和学习率。

c.将初始化后的NARX神经网络参数代入其中，再初始化CSA算法中变色龙的位置，以RMSE的值作为模型评价结果，每次迭代都更新变色龙的位置、眼睛的旋转角度和弹舌速度，根据方向评价指数ri与变色龙对猎物的感知概率Pp比较大小的结果，来判断变色龙是继续前进或是更换搜索方向。最后，返回1组最优评价结果的参数。

d.以步骤c中返回的参数作为NARX神经网络模型的最优参数，代入模型中，将模型重新初始化。

e.将训练集输入步骤d中初始化后的NARX神经网络模型对模型进行训练，使用该组预测结果与验证集进行对比来判断模型性能。

2 实验数据分析

2.1 数据来源

本文以1台现场测试的电梯钢丝绳张力作为计算数据。该电梯具体参数如表1所示，本次实验共记录了33组电梯上行时钢丝绳张力数据的变化，如图3所示。在本文中用前面的25组数据训练时间序列分析模型，然后用剩余的8组数据计算模型的精度，用于评价不同时间序列预测方法的有效性。

表1 测试电梯的具体参数

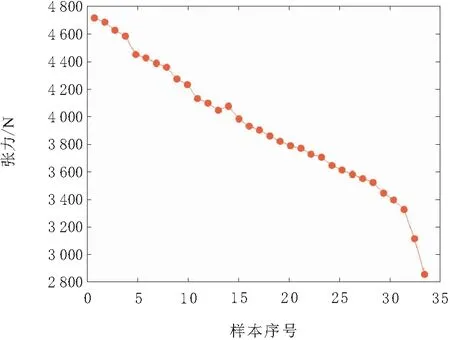
图3 电梯上行钢丝绳张力测试数据

2.2 CSA-NARX模型预测与对比

本文分别利用ARMA和LSTM对上述实测电梯上行工况下的动态张力数据进行分析。ARMA是由自回归模型(AR模型)与滑动平均模型(MA模型)为基础混合构成，其预测结果如图4a所示。LSTM是一种特殊的循环神经网络(RNN)，主要解决了训练过程中与梯度有关的问题，其预测的结果如图4b所示。图4、图5预测样本序号1～8对应图3中样本序号26～33。从图4可以看出，常用的ARMA模型和LSTM模型对8个预测样本的分析效果欠佳，其主要原因是ARMA要求待分析的时序数据具有典型的平稳性，显然其不适宜分析电梯上行测量的钢丝绳动态张力数据，另外LSTM需要假设数据是序列相关的，并且其计算过程复杂。

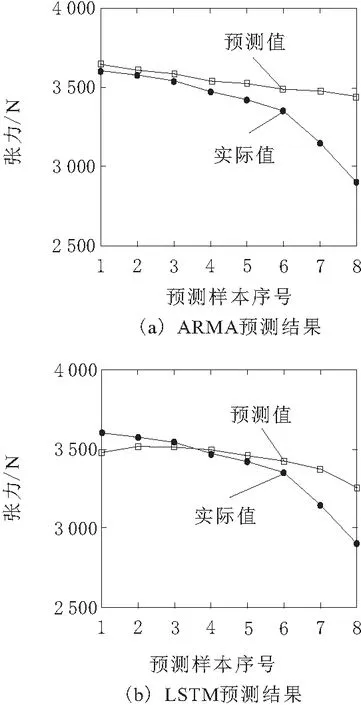
图4 常用预测模型的结果比较

然后，利用本文提出的CSA-NARX方法对钢丝绳动态张力数据进行分析，其结果如图5所示，从图5中可以发现除了变化规律相同之外，预测数据与验证数据的吻合度同样很高。原因是本文提出的CSA-NARX模型中，NARX神经网络模型是一种闭环训练的神经网络模型，可以将历史输出数据作为下一时刻的输入数据进行训练，大大提高了对历史数据的敏感性，尤其是对时间序列的数据效果尤佳。同时本文用变色龙优化算法对NARX神经网络模型的参数进行寻优，让参数得到优化后模型训练与预测效果更佳。在这2种优点的叠加下，本文提出的CSA-NARX神经网络模型尤其适合分析像电梯钢丝绳张力动态变化的预测问题。

图5 CSA-NARX对钢丝绳张力的预测结果

为了定量评价不同时间序列分析方法对钢丝绳动态张力数据的预测分析效果，本文利用均方根误差RMSE和回归系数R2作为定量评价指标。计算结果如表2所示，可以发现本文方法具有更好的预测精度和模型泛化能力，可以用于电梯曳引钢丝绳动态张力数据的预测分析。

表2 不同时间序列分析模型的预测精度比较

3 结束语

电梯在运行过程中存在许多安全隐患，尤其以钢丝绳的安全隐患为主。为了预测电梯钢丝绳上的动态张力，本文基于NARX神经网络模型，利用变色龙优化算法对模型参数进行优化，提高了模型的预测精度以及稳定性。本文提出的CSA-NARX模型具有预测精度高、寻优快、反应迅速和稳定性好等优点，在时间序列预测相关问题上有出色表现。本文利用电梯空载上行过程中钢丝绳张力的数据，分别利用ARMA模型、LSTM模型与CSA-NARX模型进行训练，将预测评价结果进行对比，发现CSA-NARX模型在电梯钢丝绳动态张力预测问题上较传统时间序列预测模型具有更好的效果，表明本文提出的CSA-NARX模型在时间序列预测领域具有良好的潜力。