黄土高原苹果园蒸腾导度大气驱动规律比较
陈 帅,党宏忠,*,丛日春,王檬檬,李明阳,刘春颖
1 中国林业科学研究院荒漠化研究所, 北京 100091 2 中国林业科学研究院生态保护与修复研究所,北京 100091 3 内蒙古农业大学沙漠治理学院, 呼和浩特 010018
在陆地生态系统中,森林植被因具有强大的碳汇、保持水土、防风固沙等生态功能而受到广泛关注[1]。人工植被如我国的“三北”防护林、“退耕还林”、“京津风沙源治理”、“长江上中游水土保持重点防治”;非洲的“绿色长城”等工程,在改善区域乃至全球生态环境中扮演着重要角色并做出了巨大贡献[2—4]。但另一方面,在气候变化背景下,随着极端气候事件频度和强度的持续增加,全球森林衰退、死亡事件频发,其中,干旱被认为是造成树木衰退、死亡的最主要的环境因素[5—6]。人工植被由于其系统组成与结构相对单一,因此遭受衰退的风险更大[7]。
气孔调节被认为是植物应对干旱胁迫的重要方式与途径,植物通过气孔调控冠层蒸腾过程、避免过度失水并保持组织的水势在阈值之上而防止出现水力衰败[8—9]。树木的气孔调控行为一般通过对叶片气孔导度、冠层导度、冠层气孔导度等指标的观测或计算而得到较好的反映[10—11]。其中叶片气孔导度(gs,mol H2O m-2s-1),即单位时间内单位叶片面积对水汽的传导程度,是叶片尺度上量化气孔行为的重要参数[12]。但在实践中,gs往往较难实现多叶片、长期、连续观测,因而限制了其在较大时空尺度研究中的运用。冠层导度(Gc,m/s)为气孔行为在冠层尺度上的表现,是冠层尺度衡量植被冠层水汽传输的重要变量[13],在实践中往往通过对植被蒸腾过程的观测(如基于单株树干液流通量的观测或涡动通量的观测),采用Penman-Monteith公式的逆转形式推导计算[14]。该公式整合了植物生理性状和微气象因子[13],综合考虑了冠层气孔阻力和空气动力学阻力对冠层水汽通量的影响[15—16],理论上能够较准确的模拟植被冠层水汽传输特征;但存在着计算公式相对复杂、包含变量相对较多,且其中计算空气动力学导度时包含参数假设的不足。在实践中,对于特定自然地理区域(如高纬度地区)的特定植被类型(如针叶林等),植被冠层被认为与大气间耦合紧密,空气动力学阻力趋于零,对冠层水汽的传输影响较小,此时Gc被简化为Gs(冠层气孔导度,m/s)而被广泛应用[17—19]。Gs是否比Gc更能恰当地反映植被冠层实际的水汽传输过程,目前的研究缺少直接的比较与验证。
经济林由于其栽植密度相对较小,株间距离相对一致,不同植株个体冠层间的干扰相对较小,树高较低,利于冠层叶片气孔导度的测定,是研究树木水分利用过程与大气驱动间关系较理想的对象。本研究以黄土区苹果园苹果树为研究对象,开展果树树干液流和周围环境因子的定位监测,计算Gc和Gs。通过对gs的测定,验证了由模型推导计算的Gc和Gs在表征实际的冠层水汽传输的准确性,并分析了三种水汽导度变量在反映树木水分利用过程对大气驱动响应时的一致性与差异,为进一步明确树木冠层水汽传输特征,揭示树木水分利用机制提供重要科学依据。
1 材料与方法
1.1 试验地概况
试验样地位于黄土残塬沟壑区的山西省吉县(110°35.655′ E,36°04.739′ N),海拔910 m。该地区属暖温带大陆性季风气候,年均气温10.2 ℃,年均日较差11.5 ℃,多年平均降水522.8 mm,10 ℃以上的有效积温3361.5 ℃,多年平均日照时数2538 h。土壤机械组成以粘粒和粉粒为主,分别占42.6%和41.6%。1 m内土层平均土壤容重为1.34 g/cm3,土壤有机质含量平均为0.85%。所选样地果园为2000 年建植,面积1.7 hm2,品种为红富士,砧木为海棠,树形为自由纺锤形,栽植密度4 × 6 m,林冠高平均为2.5 m[20]。果园布设有防雹网,经营管理措施完备,果树处于经济成熟期。
1.2 气象要素观测
于果园中央立一高约3 m竖杆架设小型气象站,安装空气温、湿度传感器(AV- 10TH,AVALON,USA)、风速传感器(AV- 30WS,AVALON,USA)、风向传感器(AV- 30WD,AVALON,USA)、大气压(AV- 410BP,AVALON,USA)、雨量传感器(AV- 3665R,AVALON,USA)、太阳总辐射传感器(AV- 20P,AVALON,USA),净辐射传感器(NR-LITE2,Kipp & Zonen,Netherlands),监测果园树冠上方空气温度(Ta)、相对湿度(RH)和太阳总辐射(Ra)等气象要素。于竖杆附近距地表约5 cm处埋设土壤热通量(G)传感器(HFP01,Huk Sefflux,Netherlands)。以上传感器均连接SQ2020数采器(Grant,UK),采样间隔为10 min,记录间隔为30 min。
大气水汽压亏缺(VPD)计算公式[21]:
(1)
式中,Ta:大气温度(℃);RH:空气相对湿度(%)。
1.3 树干液流监测
采用Granier式热扩散传感器(TDP- 3 cm,Plantsensor,AUS)监测苹果树完整生长季(2018年4月1日—2018年10月31日)的树干液流速率。该传感器由上、下两根探针组成,上部探针为加热探针,下部为参考探针。2018年3月份,选定3株冠形完整、生长健康的果树样株(表1),于其东、南、西、北四个方位各安装一套TDP- 3cm,安装过程及技术要点见文献[22],并使用铝箔防辐射膜包裹树干安装探针部位。12套TPD传感器均接入32通道SQ2040数采器(Grant,UK),采集、记录间隔分别为10、30 min。采用100 W太阳能板接12V- 100 AH铅酸蓄电瓶连续供电。采用Granier经验公式[23]计算液流速率(Js、cm/h):
(2)
式中,ΔT:上下两探针间实际温差(℃);ΔT0:液流为零时上、下两探针间的温差(最大值,℃),该值采用两次回归法确定[24]。

表1 样树概况
对4个方位Js观测值取平均得¯Js作为单株果树液流速率平均值,计算果树冠层蒸腾速率(Ec,mm/h):
(3)
式中,Ag:样树冠层地面垂直投影面积(cm2);As:样树边材面积(cm2),通过苹果树边材面积—胸径(DBH,cm)关系式[20]求得:
As=0.61×DBH1.941
(4)
1.4 叶片气孔导度测定
于苹果树耗水旺盛的果实膨大期选择连续三个晴日(2018年5月29日—31日)的5:00—20:00时段,利用Li- 6400便携式光合仪(Li-Cor lnc.,Lincoln,USA)每隔1 h测定样树叶片气孔导度(gs,mol H2O m-2s-1)。对上述每样株选取3—5片完整、健康叶片做好挂牌标记,每次每片样叶连续测定30次,记录气孔导度和基于叶片温度计算的水汽压亏缺(VPDL,kPa)等指标。依据公式(5)[25]将gs的单位由“mol H2O m-2s-1”转换至 “m/s”:
(5)
式中,Ta:大气温度(℃);P:大气压强(kPa)。
1.5 冠层导度、冠层气孔导度与脱耦联系数计算
冠层导度(Gc,m/s)的计算基于Penman-Monteith公式[13,26]:
(6)
式中,Ec:冠层蒸腾速率(mm/h,由公式(3)计算);λ:水的蒸发潜热(2.45 MJ/kg);Δ:饱和水汽压随温度变化曲线斜率(kPa/℃);Rn:净辐射(MJ m-2h-1);G:土壤热通量(MJ m-2h-1);Ktime:时间转换系数(3600 s/h);ρa:干空气密度(1.25 kg/m3);cp:空气定压比热(1.013×10-3MJ kg-1℃-1);VPD:大气水汽压亏缺(kPa);γ:干湿表常数(0.0674 kPa/℃);Ga:空气动力学导度(m/s),由公式(7)[27]可得:
(7)
式中,k:Karman常数(k=0.41);u:相对高度z处(本研究为3 m)的风速(m/s);d:零平面位移高度(m);z0:表面粗糙度(m);d=0.75h、z0=0.1h,h为样树平均株高(本研究为2.43 m)。冠层导度(Gc,m/s)计算公式[28]:
(8)
由于在阴、雨天VPD及Rs较低,计算冠层导度会产生较大误差,因此为更准确反映Gc常规水平,本研究选取典型晴天白天(从太阳辐射日变化曲线判断),且符合VPD>0.6 kPa、Rs>50 W/m2条件下的数据计算冠层导度[29]。
冠层气孔导度(Gs,m/s)的计算公式[10—11,17]:
(9)
脱耦联系数(0<Ω<1,无量纲)计算公式[26,30]:
(10)
Ω越接近于0,表示冠层与大气间的耦合越紧密。
1.6 数据分析
当土壤水分不受限制时,Gc、Gs、gs与VPD间的关系一般符合以下模型[31](对于gs,用VPDL代替VPD):
G=Gsrief-mlnVPD
(11)
式中,G为三种水汽导度变量中的一种,Gsrief是参比导度(VPD(VPDL)=1 kPa时的G值),m为G对VPD(VPDL)的敏感性,即dG/dlnVPD(VPDL)。本研究采用此模型对Gc、Gs、gs与VPD(VPDL)散点分布的上边界进行非线性拟合。
将VPD以0.1 kPa间隔分段(“四舍五入”法使VPD保留1位小数,VPDL以0.5 kPa间隔分段),分别统计各段VPD(VPDL)中Gc、Gs和gs的平均值(分别记为Gc-mean、Gs-mean、gs-mean),采用Log-Normal模型(公式12)对Gc-mean、Gs-mean随VPD的变化进行拟合(gs-mean由于数据观测时间短未进行拟合)。
(12)
式中,a、b、c和σ为常数。
采用Origin 2021b(OriginLab, USA)进行单因素方差分析、相关分析等统计分析并制图,采用R- 3.6.1软件分位数回归Quantreg包(https://cran.r-project.org/web/packages/quantreg/)进行边界函数拟合[32]。
2 结果与分析
2.1 Gc、Gs与Ω 季节动态

图1 生长季(4—10月)主要变量的季节变化过程Fig.1 Seasonal variation of main variables in growing season (April—October)图中不同小写字母表示在0.05显著性水平下差异显著;脱耦联系数为无量纲变量
生长季(4—10月)期间,Js、Gc、Gs、Ω 及VPD各变量均存在显著的季节变化(P<0.05)(图1)。Js总体呈先增后减的季节变化趋势,8月份的平均值最大((9.93±2.66)cm/h,平均值±标准差),4月份最小((6.54±2.98)cm/h)。Gc月均值在10月份达到(0.00185±0.00059)m/s,显著高于其它月份(除9月份外,P=0.28),在6月份最小,仅为(0.00108±0.00049)m/s,显著低于其它月份(P<0.05)。Gs的月变化趋势与Gc总体上相一致,但各月Gs均显著高于Gc(P<0.05)。10月份Gs平均值最大,为同月Gc的1.4倍;6月份Gs平均值最小,为同月Gc的1.5倍。Ω月平均值最大值、最小值分别出现在8月和4月,其值分别为0.17±0.11、0.07±0.05。VPD总体呈先增后减的季节变化趋势,其在6月份最高((2.71±1.11)kPa),10月份最低((1.45±0.40)kPa)(图1)。
2.2 Gc、Gs、Ω与VPD的日变化过程
对Gc、Gs、Ω与VPD等变量在日间的动态变化进行统计发现,在白天(6:00—18:00),Js、Gs、VPD随时间的变化过程呈“单峰型”,而Gc、Ω的变化呈“先增后减,午后(14:00)抬升”的“双峰型”曲线(图2)。Js在6:00时的值最小((0.67±1.02)cm/h),约在12:00时达到峰值((10.22±1.85)cm/h),随后递减,18:00时的Js值是6:00时的9.3倍。Gc最小值(Gc-min)出现在6:00((0.00047±0.00078)m/s),于10:00升至峰值,约为Gc-min的3.5倍,随后递减,于14:00达波谷后逐渐抬升,至17:00时出现第二峰值。Gs最小值(Gs-min)出现于6:00((0.00046±0.00070)m/s),峰值出现于10:00,随后递减,18:00的Gs值约为Gs-min的3倍。白天大部分时段(7:00—16:00),Gs显著高于Gc(P<0.05)。Ω日变化趋势与Gc相似。VPD的最小、最大值分别出现在6:00((0.68±0.07)kPa)、15:00((2.54±0.80)kPa)。Gc、Gs的峰值时刻较Js的提前约2 h,较VPD提前约5 h(图2)。

图2 主要变量日间的变化过程(6:00—18:00)Fig.2 Diurnal course (6:00—18:00) of main variables图中数据为平均值±标准差
2.3 Gc、Gs与Js间的关系
对Gc、Gs两种导度的变量随Js的变化进行分析发现,总体上Gc、Gs与Js间呈正相关关系(图3)。Gc与Gs随Js变化分布具有确定的上、下边界线,并且Gs随Js变化的相关性高于Gc随Js变化的相关性。对一日内Gc、Gs和Js随时间推进的变化趋势分析显示,Gc、Gs与Js联动变化存在“磁滞回环”效应,即其上升路径与下降路径不重合,回环曲线基于时间发展呈顺时针方向(图3)。
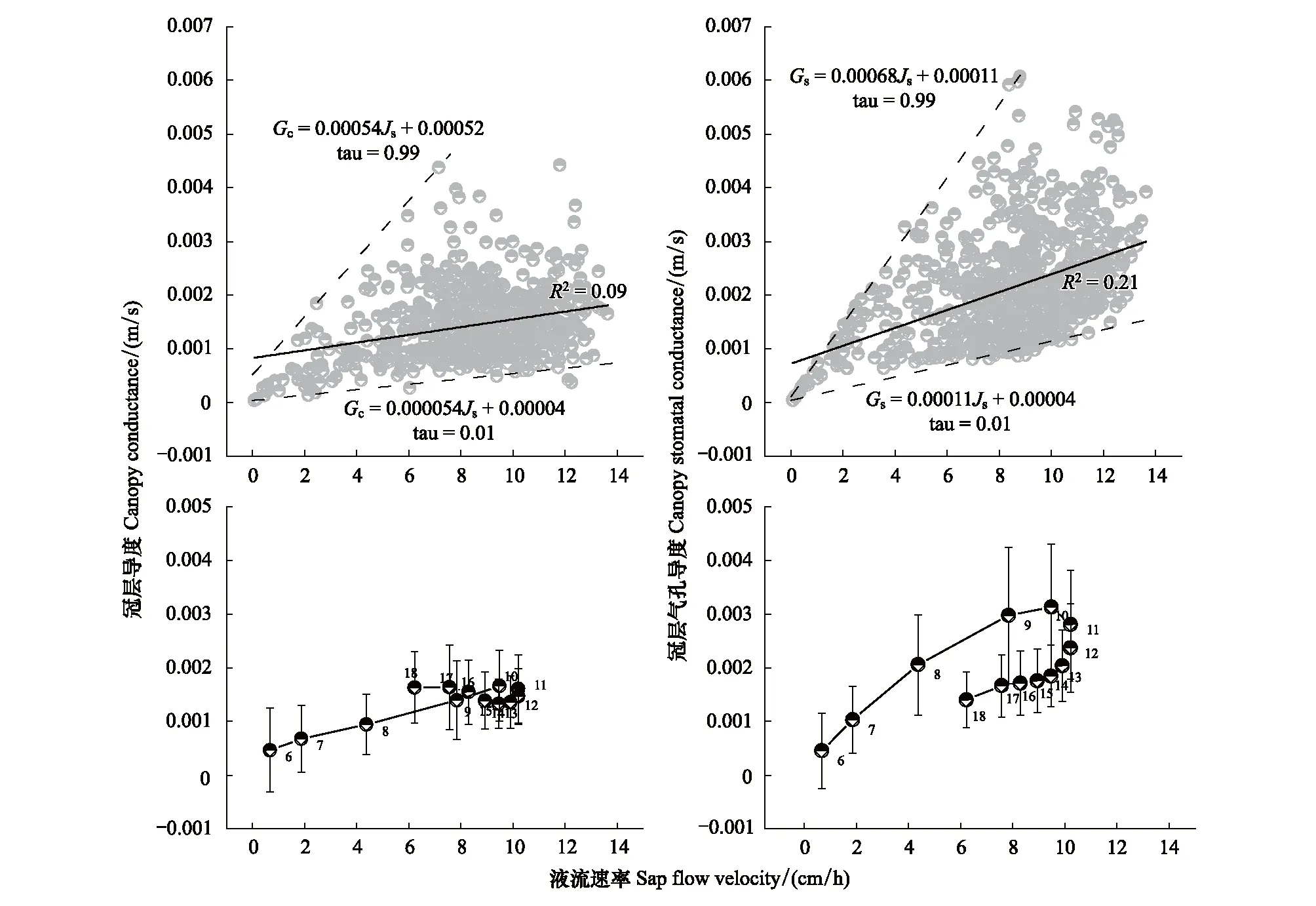
图3 冠层导度、冠层气孔导度与液流速率的关系Fig.3 Relationships between canopy conductance, canopy stomatal conductance and sap flow velocityGc:冠层导度 Canopy conductance;Gs:冠层气孔导度 Canopy stomatal conductance;Js:液流速率 Sap flow velocity;图中数字6—18表示时刻6:00—18:00
2.4 Gc、Gs与gs日变化过程中的关联
选取与gs测定同期(5月29、30、31日)的Gc、Gs值进行关联性分析发现,日间(6:00—18:00)Gs、gs值较为接近,而Gc则在午间前后低于Gs、gs(图4)。一日内Gc、Gs、gs峰值的平均值分别为(0.00180±0.00056)、(0.00403±0.00117)、(0.00393±0.00116)m/s。多重比较结果显示,一日内gs与Gs间无显著差异(P>0.05),而gs在14:00前显著高于Gc(P<0.05)。Gs与gs间具有较好的线性关系,其中在清晨开始的短时间内(6:00—8:00)快速上升(斜率为1.3661,R2=0.95),之后的很长时间内(8:00—18:00)递减(斜率为 0.9136,R2=0.98)。Gc与gs间的线性关系不明显(图4)。

图4 典型晴天白天(6:00—18:00)冠层导度、冠层气孔导度与叶片气孔导度间的关系Fig.4 Relationship between canopy conductance, canopy stomatal conductance and leaf stomatal conductance in a sunny day (6:00—18:00)
2.5 Gc、Gs、gs对VPD(VPDL)变化响应关系的比较
Gc、Gs、gs随VPD变化的上边界均呈对数函数递减关系(图5)。对Gc、Gs、gs分别以VPD值以0.1 kPa间隔分段(VPDL以0.5 kPa间隔),计算各段的平均值(Gc-mean、Gs-mean、gs-mean)后与VPD进行拟合(因gs-mean数据量较小、未开展拟合),结果表明:Gc-mean、Gs-mean和gs-mean随VPD变化均呈现先增后减的变化趋势(图5),其中Gc-mean、Gs-mean与VPD分别符合Log-Normal函数关系:
(13)
(14)
拟合函数式的拐点对应的VPD值分别为1.33和1.16 kPa;gs-mean变化的拐点约在VPDL为1.30 kPa。Gc-mean、Gs-mean、gs-mean峰值分别为0.00187、0.00301和 0.00420 m/s。在一日内,Gc、Gs、gs随VPD(VPDL)而变化的规律并不一致,午后(14:00)开始,Gc随着VPD的下降呈递增,而Gs与gs均呈递减的趋势(图5)。
2.6 Gc与Gs间关系随Ω水平的变化
将Ω按0.05的间隔从小到大分为5个级别:0—0.05(n=73)、0.05—0.10(n=278)、0.10—0.15(n=201)、0.15—0.20(n=76),0.2—1(n=58),对不同Ω级别下的Gc与Gs间的关系进行分析。结果显示,在Ω各级区间,Gc随Gs变化的线性回归斜率随Ω分级的递增而递减,各级拟合直线的斜率分别为:0.83(R2=0.94)、0.68(R2=0.76)、0.52(R2=0.53)、0.24(R2=0.19)和-0.08(R2=0.01),但回归斜率均低于1.0,表明在各级别下Gs一般高于Gc(图6)。

图5 冠层导度、冠层气孔导度和叶片气孔导度与水汽压亏缺间的关系Fig.5 Relationships between canopy conductance, canopy stomatal conductance, leaf stomatal conductance and vapor pressure deficitGc-mean:冠层导度平均值 Means of canopy conductance;Gs-mean:冠层气孔导度平均值 Means of canopy stomatal conductance;gs-mean:叶片气孔导度平均值 Means of leaf stomatal conductance;图中蓝色虚线为上边界函数拟合曲线,黑色实线为平均值拟合曲线;水平线和垂直线分别表示相应变量的标准差,数字6—20表示时刻6:00—20:00

图6 不同脱耦联系数级别下冠层导度与冠层气孔导度间的关系Fig.6 Relationships between canopy conductance and canopy stomatal conductance in different decoupling coefficient rangesΩ:脱耦联系数 Decoupling coefficient;图中灰色虚线为函数y=x参考线
3 讨论
3.1 Gc、Gs与gs的一致性与差异
Gc通过整合植物生理性状和微气象因子、综合考虑冠层气孔阻力和空气动力学阻力计算的水汽传输速率进而用于反映冠层蒸腾状况,具有明确的优越性[13,19,33],但在实际应用中,由于关于空气动力学Ga相关参数及土壤热通量等参数在数据获取与计算上的复杂性,限制了其实用性。因此,Gc往往被简化为Gs而广泛应用[10,26,34—35]。一般认为Gs是理想环境条件下的Gc值(即Gc的上限),Gs的值一般要高于Gc[16]。本研究以苹果树为例,证实了树木日间Gs显著大于Gc的普遍规律(P<0.01)。关于冠层水汽传输的日变化,大部分研究报道认为Gc日变化趋势为“单峰”型,如葡萄(VitisviniferaL. cv. Sultana)[13]、樟子松(Pinussylvestrisvar.mongolicaLitv)[10]和枫树(AcerrubrumL.)[36]等,通常被解释为植物在清晨打开气孔获取CO2进行光合作用,午后由于太阳辐射和大气水汽压亏缺不断增大,植物为防止水分过度散失而降低气孔导度[37]。但在本研究发现果树Gc在日间(6:00—18:00)普遍具有先增(10:00前)后减(10:00—14:00),午后(14:00—)抬升的“双峰”型变化,这种变化在欧洲赤松(PinussylvestrisL.)[33]、野樱桃(PrunusaviumL.)[27]的Gc日变化特征研究中也有报道,反映了形成Gc日变化过程的因素的复杂性。本研究还发现,gs与Gs间呈良好的线性相关性(R2=0.80),而与Gc的线性相关性较弱(R2=0.02)。这表明,Gc虽然因考虑了大气条件所主导的空气动力学阻力而显得综合性强,但当分析冠层没有完全郁闭的植被(稀疏植被)的水分传输特征时,可能反而会产生与实际水分传输过程不相一致的问题。
3.2 冠层水汽导度对VPD变化的响应
大气水汽压亏缺(VPD)普遍被认为是调控植被冠层导度(Gc)或冠层气孔导度(Gs)变化的主要驱动或抑制因子[11,13,31,38]。已有研究表明,VPD对Gc(Gs)的响应规律主要存在两种类型,一种类型是 VPD对Gc(Gs)存在抑制效应,即Gc(Gs)随VPD的增大而减小,主要表现为Gc(Gs)对VPD增加的响应呈对数或负指数下降的趋势[13,34]。有研究发现马占相思林冠层气孔导度最大值(Gs-max)随VPD的上升呈对数函数下降[39]。本研究结果显示Gc、Gs和gs的最大边界值(Gc-max、Gs-max和gs-max)随VPD的增大而呈对数函数减小,表明VPD对Gc(Gs)的抑制效应存在着确定的边界范围。另一种类型是VPD调控Gc(Gs)存在阈值效应,即Gc(Gs)随VPD的增大呈先增后减的变化规律[40]。例如,对油蒿群落的研究表明,采用基于VPD对Gc分段平均的方法研究油蒿群落Gc对VPD的响应,结果显示VPD小于1.5 kPa时,Gc与VPD呈正相关,VPD大于1.5 kPa时,Gc与VPD呈负相关[40]。本研究结果也显示苹果树Gc、Gs和gs基于VPD(VPDL)的分段平均值(Gc-mean、Gs-mean和gs-mean)对VPD(VPDL)的响应表现为先增后减的变化趋势,呈现出VPD(VPDL)调控Gc、Gs和gs的阈值效应,阈值分别1.33、1.16和1.30 kPa。VPD对Gc(Gs)的响应规律的这两种类型之间并不矛盾,前者反映的是关系的边界趋势,只考虑VPD一种环境变量;而后者反映的是关系的实际变化趋势,有更多环境因子(如太阳辐射)会参与其中[41—43]。研究表明,当VPD <1 kPa时,侧柏(Platycladusorientalis)的Gs随光合有效辐射(PAR)的增大而增大;而当VPD>1 kPa,二者的响应关系不显著[44]。
3.3 Gc与Gs耦合特征
脱耦联系数(0<Ω<1)是评价冠层与大气耦合程度的重要参数,当Ω趋于0时,指示冠层与大气耦合良好,此时气孔行为主要受大气环境因子影响,气孔导度的变化对大气环境因子的变化响应敏感;随着Ω趋向于1,冠层与大气间逐渐脱耦,叶片表面逐渐增厚的界面层削弱了大气状况的影响,气孔对蒸腾的控制越来越依赖于自身生理活动的变化[9,30,36]。本研究中,整个生长季(4—10月)中果树的Ω平均为0.12(0.03—0.39),表明果树冠层与大气间耦合较好。随着Ω逐级减小,Gc与Gs线性回归相关性增大,意即冠层与大气间的耦合作用趋于加强。同时,随着Ω的减小,线性拟合斜率(ΔGc/ΔGs)呈增大趋势,最大可达0.83(R2=0.94),表明随着冠层与大气耦合紧密,Gc越来越趋近于Gs。
4 结论
表征树木冠层水汽传输特征的三种导度变量间既具有紧密的关联性,也表现出显著的差异。在白天的绝大部分时段中,Gs显著高于Gc(P<0.05)。Gs与Gc日峰值虽然均出现在10:00时左右,但整体上Gs的日变化呈“单峰”型曲线,而Gc则呈先增后减,午后(14:00)上升的“双峰”型曲线,反映了影响因子的复杂性。在日变化进程中,gs与Gs格局基本一致,且具有较好的线性关系,而gs与Gc间的关系不明显,相关性弱。Gc、Gs对水汽压亏缺的变化响应紧密,其最大值的分布呈典型的对数递减函数关系,而平均值则呈先增后减的Log-Normal函数关系,阈值分别为1.33、1.16 kPa。Gc与Gs整体上呈线性相关关系,其相关紧密程度随Ω的的降低而明显增加,Gc越来越趋近于Gs。相较于Gc,基于树干液流推算的Gs与实测gs具有更高的一致性,可以作为反映苹果树水分传输过程的更为恰当的变量。

