基于方向相位一致性的多源光学遥感图像匹配方法

程玉芳，李景山

(1.中国科学院空天信息创新研究院，北京 100094；2.中国科学院大学，北京 100094)

0 引言

多源遥感图像匹配是指将不同传感器、不同视角、不同时相获取的同一地域的两幅或多幅图像通过匹配算法实现自动获取图像间同名点的过程[1]。

常用的图像匹配方法主要有基于特征的方法和基于区域的方法。基于特征的匹配算法其基本思想是提取图像中显著不变的几何特征，利用描述子描述特征，然后建立相似性度量准则，根据特征之间的相似性并结合其他的约束条件进行匹配和筛选。其中，尺度不变特征变换[2](scale invariant feature transform，SIFT)的描述子具有旋转不变、亮度鲁棒、对噪声和视角的微小变化稳定等优点，在遥感图像匹配领域得到了广泛应用。基于区域的图像配准方法的主要思想是根据已知的模板图像，按照特定的相似性准则计算模板图像与搜索图像区域子图之间的相关程度，对比所有子图的相似度确定最佳的子图位置。基于区域灰度的配准方法是早期图像配准中最常用的方法，常用的相似性度量方法有互相关[3]、互信息[4]等方法。

传统的利用图像灰度梯度变化来描述几何结构的方法很容易受到图像的辐射照度和视角变化的影响。相较而言，在描述图像的结构信息方面相位一致性与人类神经视觉具有基本一致的敏感性[5]，对图像中的辐射亮度变化、对比度变化和噪声干扰等均不敏感。Ye等[6]采用相位一致性模型的强度和方向信息构建了相位一致性方向直方图(histogram of orientated phase congruency，HOPC)，利用该特征描述输入图像的几何结构信息，通过几何结构的相似性进行匹配，能有效应用于光学与SAR影像之间的配准。王新生等[7]通过相位一致性模型构造出最大索引图，在最大索引图上使用分布直方图构造特征描述符来完成图像匹配，取得了较好的实用效果。

在现有研究成果基础上，本文针对多源光学遥感图像间存在的非线性辐射畸变、几何定位差异大等问题，提出了一种利用图像相位一致性特征进行同名点预测及匹配的方法。首先，通过遥感图像自带的地理位置信息将图像划分为规则格网，通过图像的纹理结构进行相位相关得到初始的相对偏移量，以此预测同名点的空间搜索范围；然后，以特征点为中心，构建点邻域内的方向相位一致性结构特征描述符，采用傅里叶变换方法进行模板窗口的特征匹配；最后，通过最小二乘法剔除误差较大的点，得到最终的同名点对，实现图像间的自动匹配。

1 多源遥感图像匹配算法及实现

本文多源遥感图像匹配的总体算法设计如下。

1)图像分块相位一致性特征提取。将输入图像划分为W×W规则大小的格网块，通过地理位置映射对应参考影像区域并裁剪同样大小图像，利用相位一致性模型计算二者边缘图像以及待配准图像格网块中的角点图像用于角点检测。

2)边缘图像相位相关。将分割好的待配准图像块与对应基准影像格网块的边缘图像进行相位相关，将相关脉冲尖峰位置记为两张格网图像间的相对偏移量。

3)误相关剔除。利用RANSAC随机采样一致性模型作为几何约束条件，筛选出正确的相关峰，即有效的格网偏移量集合。

4)特征点提取。基于1)提取的角点图像检测输入图像中显著的特征角点，并利用非极大值抑制在输入图像上提取出均匀分布的特征点。

5)方向相位一致性特征提取。以特征点为中心，统计特征点邻域内的离散方向相位一致性特征，作为该点的特征模板。

6)几何约束及匹配。利用3)得到的格网偏移量，预测特征点在基准影像上的搜索位置，提取方向相位一致性结构特征，并将其变换到频率空间，提高模板匹配的计算效率，快速定位同名点。

7)误匹配剔除。基于最小二乘估计匹配点残差，迭代剔除，得到最终的同名点集。

匹配算法总体设计见图1。

图1 自动匹配算法实现流程

1.1 相位一致性特征提取

相位一致性(phase congruency，PC)[8]模型是通过计算局部能量函数来描述图像的结构信息，是一个无量纲量，与信号的整体大小无关，这个特性保证了相位一致性特征对于光照和对比度具有很好的不变性[9]。

Log-Gabor小波可以真实自然地描述图像的频率响应[10]，它能够利用不同方向、不同中心频率的滤波器来获取图像的局部纹理特征，因此本文选择Log-Gabor提取图像的相位一致性特征。指定方向θ、不同尺度s的Log-Gabor滤波器计算相位一致性PC(s，θ)，参照Jain[11]的方法，滤波器方向间隔选择30°，即将θ分为6个方向(0°，30°，60°，90°，120°，150°)，滤波器尺度s的最大值设置为4，共24个Log-Gabor滤波器对输入图像进行滤波，提取图像的相位一致性特征。

将待匹配遥感影像划分为W×W大小互不重叠的格网块，并通过格网左上角点的地理位置映射对应参考影像点图像坐标，裁剪同样尺寸大小图幅，计算两张小图的相位一致性特征。划分成格网块的目的一方面是适用于本文的匹配算法，另一方面也是为了加速图像的傅里叶变换过程。

1.2 边缘图像相位相关

图像信号的傅里叶变换包含幅度与相位两个部分，根据傅里叶变换相关理论[12]可知，函数位移不会改变傅里叶变换的模(幅值)，但是会改变实部与虚部之间的能量分布，其结果是产生一个与位移量成正比的相移。

因此通过计算两频谱之间的互功率谱，并进行傅里叶逆变换，得到的相位相关脉冲图像除了在它们相对偏移(u0，v0)处不为零外其余位置都基本接近零值，这样就很容易得到两幅图像之间的相对平移参数。

由于多种外部因素的影响，异源遥感影像上同一地物往往存在很大的非线性辐射差异。尽管在一定程度上相位相关算法能够容忍两幅图像间存在的非均匀辐照差异，但是随着图像间光照差异的逐渐增大，相位相关的显著度也会下降[13]。

PC图的最大矩M代表图像的边缘特征，而边缘结构具有较好的抗辐射畸变能力，地物的几何结构信息在异源影像上也基本保持不变，因此可以通过影像中的几何结构进行相关，初步获取地物间几何位置的偏移量。即可以通过计算两幅图像最大矩的互功率谱得到相位相关图像，此相位相关脉冲图像的脉冲峰位置即为两幅影像之间的偏移量(图2)(注：图2(e)中在(25，443)处有一个尖锐的峰值，两幅图像大小为500像素×500像素，左上起点坐标为(1，1)，它们的相对偏移量为(24，-58))。

图2 相位相关算法示例

为确保分块相位相关方法的有效性，还需要为算法结果设置阈值进行筛选。

1)相关强度阈值Tmag=0.03。相位相关图中最大响应峰值大小表征图像相关性的强弱程度，若响应峰值小于给定的强度阈值Tmag，则表明它们之间相关程度较弱，相关失败。

2)相关比例阈值Tratio=0.75。若相位相关脉冲图像中次响应峰值与最大响应峰值之比大于Tratio，则认为两幅图像间的相关性不够显著，判定为相关失败。

对W×W大小的格网块提取出的边缘结构特征计算相位相关图像，记录脉冲尖峰位置和其平面坐标，即为两图像之间的相对平移量。

1.3 误相关剔除

由于遥感图像的复杂性，通过几何结构信息进行相位相关也可能存在误相关情况，如大面积水域、荒漠等特征不明显区域。因此仍需对获取的初始脉冲集合进一步筛选，得到准确有效的偏移量集合。

RANSAC(random sample consensus)算法[14]通过迭代的方式从一组包含离群的被观测数据中估计出一个认为符合此样本的数学模型，从而将符合数学模型的点标记为内点(正常数据)，偏差大的点标记为外点(异常数据)。

分块相位相关得到的初始脉冲峰集合实际上表征的是输入图像各格网块与参考图像各格网块之间的相对偏移量，而整幅图像各格网的偏移量应该基本符合某个变换模型，所以本文采用RANSAC算法提纯分块相位相关结果，避免对之后的匹配过程提供错误的几何约束。

1.4 特征点提取

大多数特征检测都是通过寻找局部极值作为特征点，这会导致特征点分布受图像对比度影响在高对比度区域分布密集、低对比度区域分布稀疏的情况。

PC图的最小矩m为图像的角点特征，通过阈值T提取特征点，即：对于任意位置(x，y)，如果m(x，y)>T，则该位置将被标识为候选特征点。但直接通过设定阈值提取特征点同样会造成关键点在图像上非均匀分布。因此本文通过非极大值抑制方法，邻域极值的查询半径为r，抑制区域大小为(2r+1)×(2r+1)，剔除容易受到噪声干扰的低对比度的点，筛选出图像中高对比度的点。然后，在每d×d的格网范围内，取局部极大值中的最大值点，记录其位置信息作为最终的特征点，使检测到的关键点能够均匀分布在整幅遥感图像上。

图3为SIFT算法与非极大值抑制角点检测方法的对比图，表明非极大值抑制角点检测能够从图像中提取均匀分布的关键点。

图3 特征检测算法对比图(影像大小：1 000像素×1 000像素)

1.5 方向相位一致性特征

相位一致性的方向代表着图像结构特征沿此方向剧烈变化，类似于梯度方向，可采用Log-Gabor小波的奇对称滤波器来计算，其卷积结果表示影像在某个方向的能量变化，各个方向上的相位一致性可以反映不同方向的边缘强度信息。因此，本文利用离散方向集的相位一致性描述图像中每个点的特征。

构造不同方向的Log-Gabor滤波器与输入图像进行卷积得到各方向上的相位一致性PC(θ)，θ共6个方向(0°，30°，60°，90°，120°，150°)，即可以得到一组离散方向集的相位一致性特征图像(PCθi，i=1，2，3，4，5，6)。

图4 方向相位一致性特征提取

在构造区域的特征时，为使其更加稳定，需要充分考虑特征点邻域的结构特征。因此，本文提出一种基于方向相位一致性特征的匹配模板，构造以关键点为中心的区域方向相位一致性特征，确定模板图像半径和搜索半径大小，再对不同角度的边缘强度进行组合，形成关键点邻域的方向相位一致性特征描述子，使其能够抵抗非均匀光照变化所引起的图像间非线性辐射差异。

1.6 几何约束及匹配

考虑传统模板匹配方法逐点滑动计算，搜索范围大，计算量大，本文为了提高同名点匹配效率，先将待匹配图像与参考图像划分为规则格网块，提取边缘图像进行相位相关，获取各格网块之间的偏移参数。在特征点匹配的过程中，从已得到的偏移量中取距该特征点最近的格网相对偏移量，将其认为是该特征点与其同名点之间的几何误差，从而预测特征点对应的同名点位置，缩小搜索范围。

在左上角点经纬度及图像分辨率完全相同的情况下，特征点坐标(x，y)与预测同名点位(x′，y′)的对应图像坐标关系为式(1)。

(1)

式中：(dx，dy)表示点(x，y)的偏移量，即距(x，y)最近的有效相关峰位置。

由于特征点与其预测的同名点的区域模板的方向相位一致性特征是逐像素的结构特征描述符，数据量大，计算耗时，因此本文采用傅里叶变换将特征模板从空间域转换至频率域，加速模板匹配过程，提高匹配性能。

误差平方和算法(sum of squared differences，SSD)是一种比较经典判断模板图像与搜索图像之间的相似度度量算法，计算方法见式(2)。

SSD(x，y)=∑i∑j[S(i+x，j+y)-T(i，j)]2

(2)

式中：T为匹配的模板图像；S是搜索图像。上式展开，可得式(3)。

SSD=S*S-2S*T+T*T

(3)

式中：*为卷积运算符。第一项S*S和第三项T*T为固定值，因此可以继续将相似性度量Sim简化为式(4)。

Sim=S*T=FS×FT

(4)

式中：FS和FT分别为S、T傅里叶变换结果。当模板图像大小为N×N，搜索半径为M/2时，搜索图像大小为(M+N)×(M+N)，空间域计算SSD的时间复杂度为O(M2N2)，而将其计算过程简化到频率域，时间消耗为O((M+N)2log(M+N)，计算效率可以得到显著提升。

图5为基于方向相位一致性特征的模板匹配示例，在待匹配图像中检测到的关键点A通过几何约束条件预测其在参考图像中的同名点B’位置，分别以A、B’为中心取(M+N)×(M+N)邻域计算该区域的方向相位一致性特征，再利用傅里叶加速的误差平方和算法即可求得两模板特征间相似性，相似性最大值处即为关键点A实际对应的同名点位置B。

注：模板半径为50×50，搜索半径10×10，此时搜索图像大小为120×120。左上起点坐标为(1，1)，关键点A(61，61)的实际对应的同名点位置为B(65，59)。图5 基于方向相位一致性特征的模板匹配示例

1.7 误匹配剔除

尽管基于相位一致性特征的匹配流程已经具有较高的正确匹配概率，但在实际匹配过程中发现仍然会有部分偏差，即通过相似性度量测度之后，仍然不可避免地会有少量的错误匹配。为了剔除这些错误匹配，需要再次使用最小二乘法通过最小化误差对得到的初始匹配点集进行提纯。在通过最小二乘解算出模型参数后，计算每个点的残差，并剔除残差较大的同名点，直至残差小于阈值时退出迭代过程，得到最终的匹配点。

2 实验分析

为了验证本文方法在多源光学遥感影像匹配中的有效性，以中国遥感卫星地面站通用遥感卫星数据预处理系统生产的国产高分系列卫星遥感影像作为研究对象。参考影像数据为91卫图下载的地图数据，具有多种分辨率且影像地物清晰、定位精度高，可作为系统几何校正产品精度检验的参考基准。3组实验数据的待配准图像分别来自于高分一号宽幅相机、高分二号多光谱相机、高分七号后视多光谱相机，实验所用的输入影像数据均已经过系统几何校正，投影坐标系为UTM坐标系，参考影像也经重采样到同一分辨率下，消除了影像间的旋转差异和较大的几何差异。实验数据基本信息见表1。

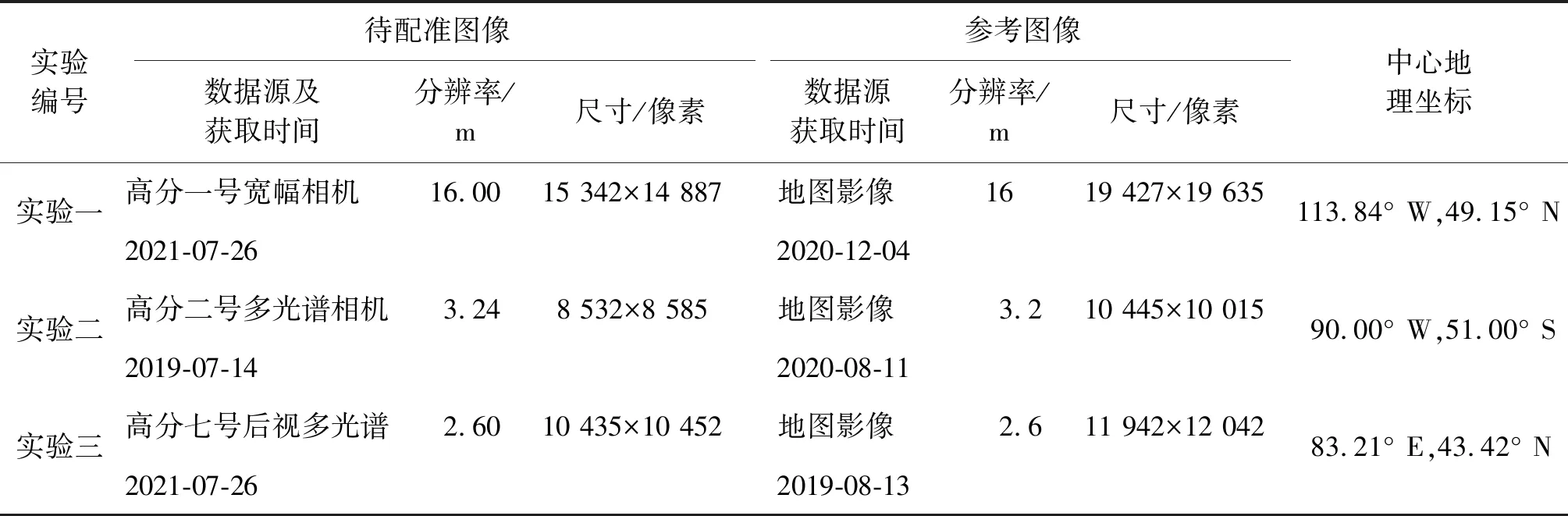
表1 实验数据基本信息

2.1 实验参数

本文特征点提取设置的检测范围为250像素，即每250×250 网格内提取1个候选点。分块格网大小设置为1 000像素×1 000像素，则每块区域最多能提取16个特征点。模板匹配的模板图像设为50像素×50像素，搜索半径为10，即搜索图像大小为120像素×120像素。借助于GDAL、FFTW等源码库，采用C++编程，设计并行程序(核心数为14)实现本文的匹配流程。为验证本文多源光学遥感图像匹配方法的有效性，实验将所提出的匹配方法与传统SIFT算法进行对比分析，SIFT实验环境参数与本文方法一致。

实验机群刀片服务器配置：Intel Xeon Gold 6 132(2.6 GHz/14 c)/2 666 MHz/10.4 GT×2，内存为16 GB DDR4 2 666 ECC REG×8。

2.2 实验结果分析

3组实验数据同时存在传感器成像物理特性、时相和辐射差异。实验一图像数据包含耕地和山脉，实验二的地物覆盖类型为耕地和水域，实验三影像中心为城市，包含大量耕地，且有部分山脉，地物信息较为丰富。3组实验数据的匹配结果见图6。表2为实验结果对比分析。

表2显示，第一组实验得到的匹配点数量基本一致，但第二组、第三组实验数据由于图像间时间间隔长，存在较大的辐射差异，SIFT匹配得到的同名点数量很少，而本文方法并未受传感器物理特性、成像角度、时相等因素的影响，仍然可以得到较多的同名点。从图6可知，本文的匹配方法在三组实验数据中得到的匹配点都能够基本均匀分布在整幅遥感图像上。

将参考影像作为输入产品的几何精度检验基准，可以看出本文方法和SIFT方法的几何精度检验结果基本接近，差距在亚像素以内，并且RMSE最大为1.03像素，说明本文的匹配方法能够达到较高的匹配精度。此外，三组实验检查到的最大几何误差为28.62像素，表明本文方法有较大的位移检测范围。

从匹配效率来讲，3组实验中本文方法耗时均大于SIFT，这主要是在相位相关及特征匹配过程中都需要计算图像4个尺度、6个方向上的结构信息。但通过并行程序设计，二者仍处于同一数量级，差距并不明显，可以满足系统几何校正产品的实时匹配需求。

图6 实验数据匹配结果图

表2 实验结果对比分析

3 结束语

对于多源遥感图像匹配来讲，相比于灰度信息，其几何结构和形状等属性更加稳定，即这些特性对传感器成像差异、光照、时相等变化不敏感。一方面，本文利用图像的边缘结构进行分块相位相关，不受图像噪声、照度变化的干扰，预测同名点位置，使得本文方法在较小的搜索半径内仍然具有较大的位移检测范围。另一方面，离散方向集的相位一致性特征可以反映不同方向上的边缘结构特征，这种特征几乎不依赖于图像灰度，因而具有很强的抗辐射畸变能力，从而能够实现同名点的精确匹配。

实验结果表明，本文方法可以有效应对多源遥感图像的非均匀辐射畸变，并克服图像间较大的几何误差，从而获得均匀分布的同名点，实现遥感图像间的自动匹配。