基于动态滑动步长改进LMD算法的砂浆脱空识别
辛欣 任尊松
基于动态滑动步长改进LMD算法的砂浆脱空识别
辛欣 任尊松†
(北京交通大学 机械与电子控制工程学院,北京 100044)
水泥沥青砂浆作为板式无砟轨道的重要结构,在列车高频动载与温度荷载共同作用下,极易发生脱空损伤。根据轮对加速度变化特征可实现砂浆脱空快速、准确定位。利用自适应动态滑动步长改进局部均值分解算法,将轮对垂向加速度分解为一系列乘积函数分量。依据峭度变化规律选取最能反映砂浆脱空特征的第1个乘积函数分量,并求其瞬时能量和标准化瞬时能量以增强砂浆脱空特征。根据瞬时能量和标准化瞬时能量的包络函数是否存在离群值判断砂浆是否脱空。结果表明:当砂浆脱空长度不超过0.30 m时,瞬时能量的包络函数在脱空处未出现离群值,导致“漏判”,而标准化瞬时能量的包络函数在脱空和未脱空处均出现离群值,导致“误判”;当砂浆脱空长度不小于0.65 m时,瞬时能量和标准化瞬时能量的包络函数均只在脱空处出现离群值,可准确定位砂浆脱空。通过车辆结构响应识别砂浆脱空,可有效缓解轨道损伤检测压力,提高车辆运营效率。
板式无砟轨道;砂浆脱空;损伤检测;信号处理
板式无砟轨道应用广泛,其主要结构包括钢轨、扣件、轨道板、水泥沥青(CA)砂浆层、混凝土底座和路基等[1]。CA砂浆作为有机-无机非金属复合材料,长期暴露于阳光和空气之中容易发生老化损伤;且列车高频动载和日夜温差荷载的共同作用,使砂浆与轨道板间时常发生脱空[2]。砂浆脱空严重影响轨道系统承载能力和服役寿命,同时威胁列车运行安全性和平顺性[3]。因此,及时定位砂浆脱空并对其进行维修,可有效延长轨道寿命、提高车辆运行性能。
胡志鹏、赵佳和胡琴等[4-6]分别通过轨道结构曲率模态、应变模态和模态振型,判断砂浆是否脱空。田秀淑等[7]建立了轨道有限元模型,基于瞬态冲击响应特性对砂浆脱空进行检测和识别。陈甜甜等[8]通过Hilbert-Huang变换和卷积神经网络对轨道冲击回波进行分析,确定CA砂浆脱空位置。陈梦[9]和李再帏等[10]分别根据弹性波和Lamb波在轨道系统中的传播状态判断砂浆是否脱空。李自法等[11]根据轨道线路旁采集的声音数据,检测砂浆脱空与否。
目前,砂浆脱空识别的主要根据是轨道板或某段轨道的结构响应。对于全线轨道健康监测而言,该方法成本高、耗时长,且检测设备安装困难。因此,为满足轨道线路里程不断增加的需求,利用车辆振动响应识别轨道损伤已成为研究热点。该方法通过实时检测线路健康状态,将轨道传统周期维修替代为状态维修,提高线路维护效率、降低维护成本。Shi等[12]基于多尺度平均小波能量分析轮对加速度,以单块轨道板长度响应为单元,构造砂浆脱空指标。该方法具有非自适应性,且难以准确定位脱空位置。由于轮对加速度较构架和车体加速度对砂浆脱空更加敏感,故本研究也将利用轮对加速度识别砂浆脱空。
常用信号时频分析方法包括短时傅里叶变换(STFT)、Wigner-Ville分布(WVD)、小波变换(WT)、经验模式分解(EMD)和局部均值分解(LMD)[13-14]等。STFT和WT具有非自适应性,WVD会产生交叉干扰项;EMD和LMD因具有自适应性得以广泛应用。与EMD相比,LMD不存在负频率,且能将信号分解为较少阶数,使每阶分量保留更多有效信息,突出损伤特征,故LMD更具优势[15-16]。在LMD算法中,局部均值函数和包络估计函数拟合方法的选取至关重要。Smith[14]利用滑动平均法(MA)逐步平滑局部均值和局部包络估计值。Sun等[17]通过加权系数改进MA,但仍无法确定最佳滑动步长。为提高插值精度,Zhang、Deng、Li、Chen等[18-21]分别采用具有高阶连续导数的分段线性插值、三次样条插值、有理样条插值及三角基样条插值等替代MA。但上述插值方法需要较高插值节点密度且容易出现过包络和欠包络。
本研究根据LMD分解过程中待平滑信号的瞬时幅值变化情况动态确定滑动步长,避免出现局部极值。通过改进LMD算法将轮对加速度分解为一组乘积函数分量。依据峭度变化选取包含砂浆脱空信息最多的第1个乘积函数分量,计算其瞬时能量和标准化瞬时能量以突出砂浆脱空特征。最后,利用瞬时能量及标准化瞬时能量的包络函数结合离群值确定砂浆脱空位置。
1 局部均值分解
1.1 算法流程
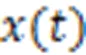
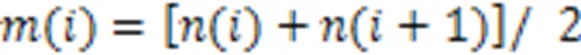
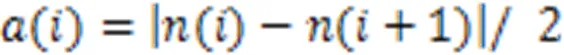
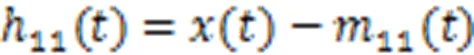

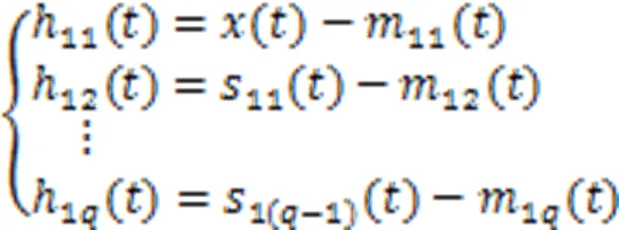




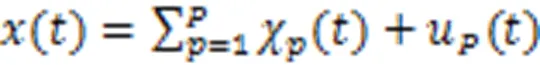
1.2 自适应动态滑动步长确定
1.2.1滑动平均法
(2)选取滑动步长,利用滑动均值代替原序列值,如式(11)所示:
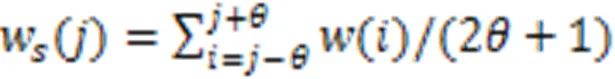
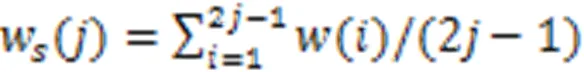
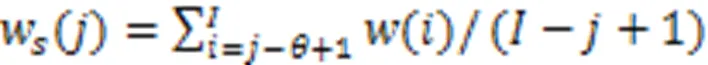
1.2.2自适应滑动步长确定
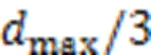
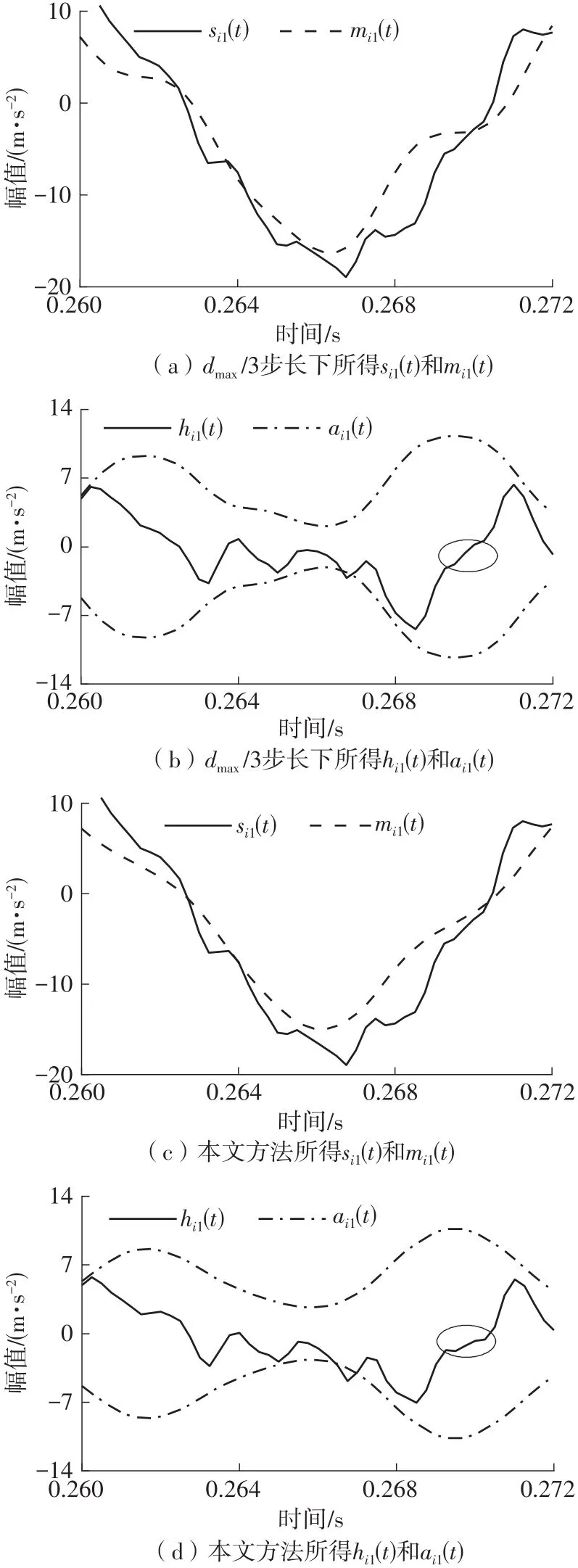
图1 LMD首次分解时部分结果对比

图2 LMD分解过程中部分结果对比
基于上述现象,本研究提出以下两个定义,建立自适应滑动步长公式。


2 信号特征增强
2.1 瞬时能量和标准化瞬时能量
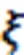
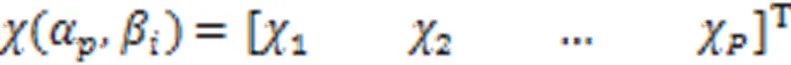

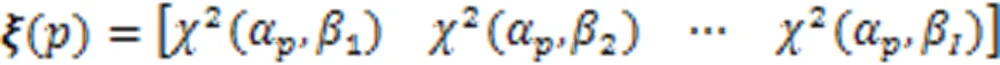
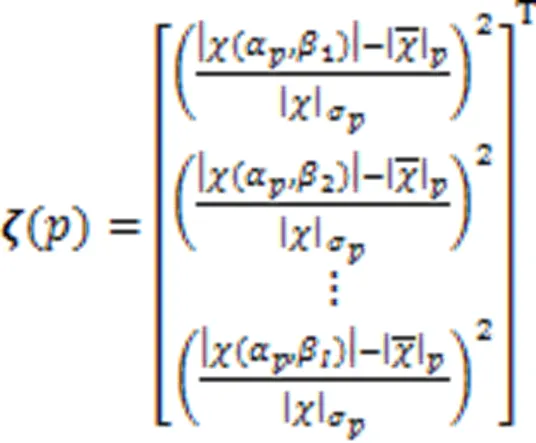


2.2 包络函数及离群值

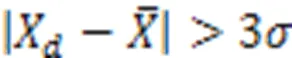
若能根据轮对加速度相关信号是否存在离群值判断砂浆是否脱空,可极大地提高轨道损伤检测效率。由于砂浆脱空主要是使瞬时能量和标准化瞬时能量幅值发生变化,为清晰表示信号特征变化规律,可先寻其极大值序列,计算包络函数,再判断是否存在离群值。
3 砂浆脱空识别
3.1 仿真数据来源

图3 车辆-轨道耦合动力学模型

图4 砂浆脱空示意图
3.2 LMD分解结果

为选取有效分量进行砂浆脱空识别,根据式(19)计算轮对垂向加速度及其分量能量。经计算可知,改进LMD算法中,前两阶分量能量之和已达轮对加速度能量90%以上,包含绝大多数轮对加速度信息。故可忽略后几阶分量,仅利用1和2进一步分析轮对加速度特征。
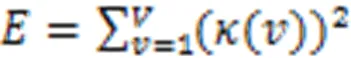
峭度作为信号冲击特性评价指标,对局部性缺陷特别敏感[24],其计算公式如(20)所示。表1示出了不同砂浆脱空工况下,轮对加速度1和2峭度值。由表1可见,随着砂浆脱空长度增加,1峭度明显增大,2峭度波动较小。故1对砂浆脱空更为敏感,即砂浆脱空信息主要集中于1分量中。
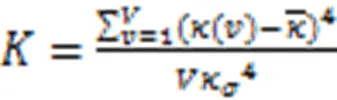
式中,和分别为的均值和标准差,K为峭度。
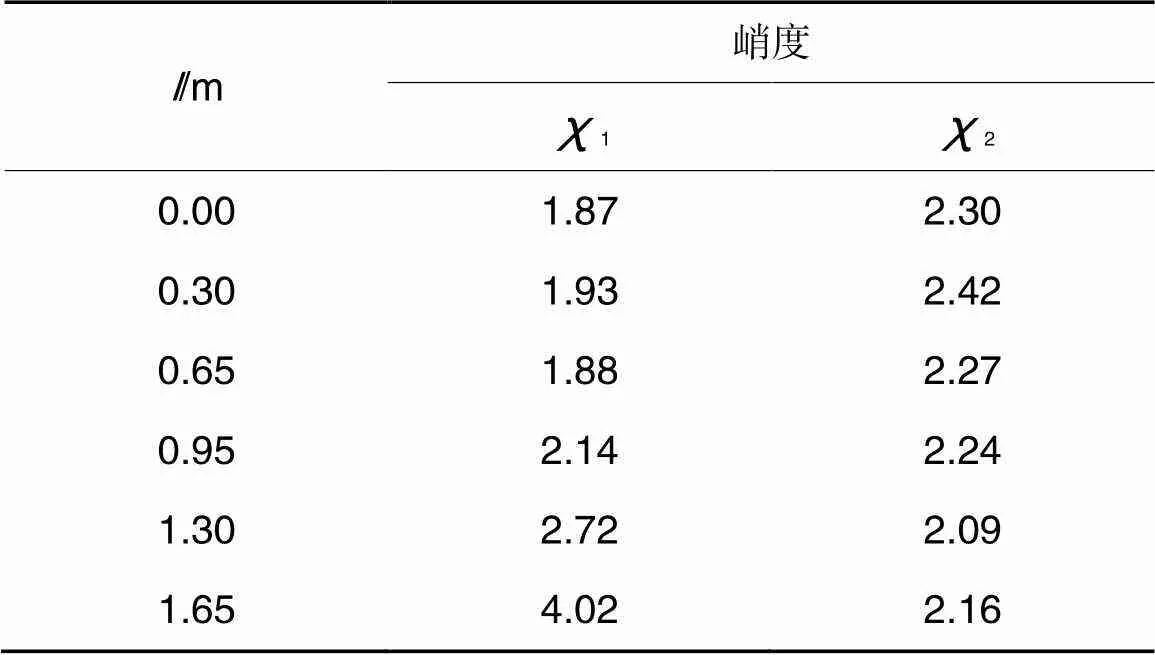
表1 χ1和χ2峭度对比表
3.3 瞬时能量及标准化瞬时能量
图6示出了不同砂浆脱空长度下轮对加速度1分量的时程曲线。由图可见,当砂浆脱空长度不超过0.65 m时,1分量在脱空位置处(0.28 s附近)并未产生明显差异。当砂浆脱空长度达到0.95 m时,1分量在脱空位置处出现较大波动。随着脱空长度的增大,脱空处1幅值逐渐增大,但增幅较小。
图7和图8示出了各工况下1瞬时能量和标准化瞬时能量。当砂浆脱空长度不超过0.30 m时,瞬时能量及标准化瞬时能量幅值在砂浆脱空位置处,均未出现明显峰值。不同于图6中脱空0.65 m时的1分量结果,图7和图8中,砂浆脱空0.65 m时,瞬时能量和标准化瞬时能量在砂浆脱空位置处产生较大峰值。且相对于瞬时能量,标准化瞬时能量在脱空处峰值更加突出。
作为冲击信号衡量指标,峭度越大,表明信号中冲击成分表现越明显。为对比1及其瞬时能量和标准化瞬时能量对砂浆脱空的表现效果,计算不同砂浆脱空工况下,上述响应较无脱空工况下的峭度值变化率:

图6 各工况下χ1时程曲线
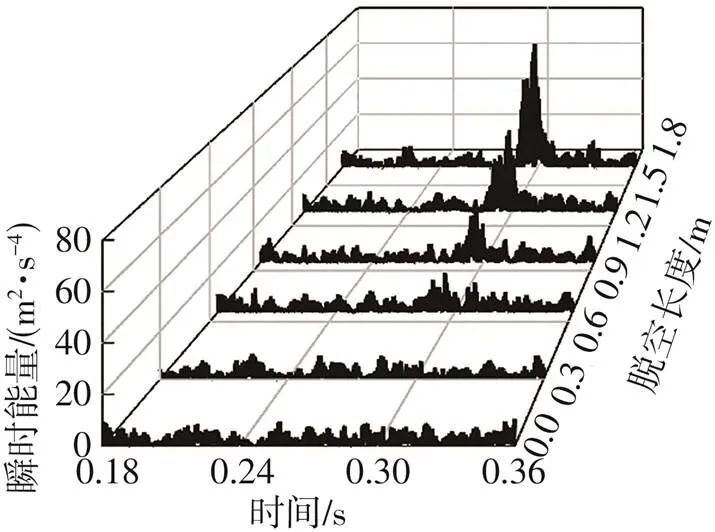
图7 不同工况下的瞬时能量时程曲线

图8 标准化瞬时能量
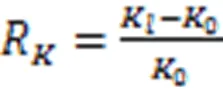
图9示出了不同砂浆脱空工况下1及其瞬时能量和标准化瞬时能量的峭度值及峭度变化率。随着砂浆脱空长度的增加,各表现形式峭度值均不断增大,但增长速度略有差异。当砂浆脱空长度不大于0.30 m时,1分量、瞬时能量和标准化瞬时能量峭度值均无明显变化,其变化率不足6%。1分量峭度随砂浆脱空长度增加变化幅度最小,砂浆脱空长度达到1.65 m时,其最大变化率仅为114.65%。砂浆脱空长度为0.65 m时,瞬时能量及标准化瞬时能量峭度变化率分别达40.18%和135.67%。当脱空长度不小于0.95 m时,瞬时能量和标准化瞬时能量峭度值较无脱空条件下分别增大285.98%和673.20%以上。由此可见,标准化瞬时能量突出砂浆脱空信息能力最强,据其判断砂浆是否脱空具有明显优势。
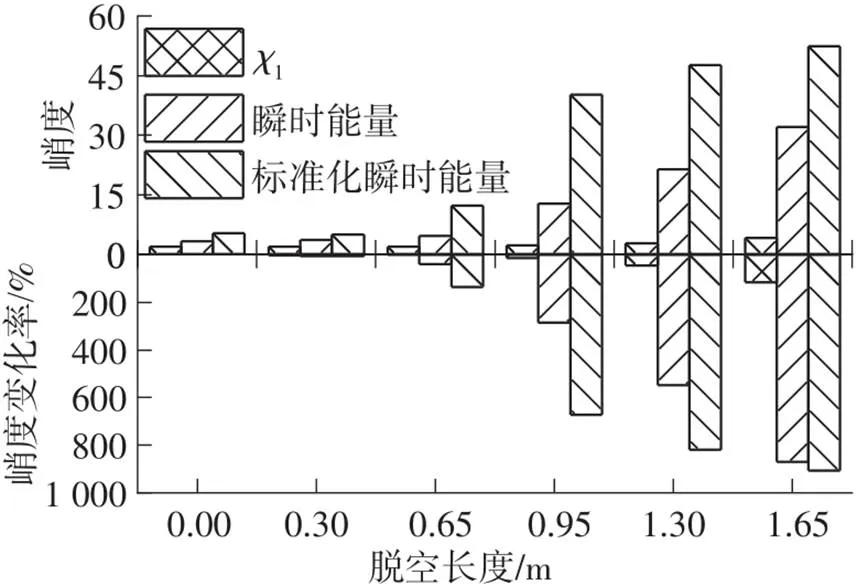
图9 不同工况下χ1及其瞬时能量和标准化瞬时能量峭度对比
3.4 包络函数及离群值
由上述分析可知,砂浆脱空引起1及其瞬时能量和标准化瞬时能量幅值变化。为便于观察1及其瞬时能量和标准化瞬时能量幅值变化趋势,取其包络函数,并计算其离群限值。依据包络函数是否存在离群限值,判断砂浆是否发生脱空。


图10 不同工况下瞬时能量包络函数及其离群限值

由于砂浆脱空长度大于0.95 m时,标准化瞬时能量与瞬时能量包络函数结果相似,均在砂浆脱空处出现离群值,故仅给出脱空长度不超过0.65 m时的标准化瞬时能量包络函数及其离群值,如图11所示。当砂浆脱空长度为0.30 m时,在脱空与未脱空处均出现离群值。此时,若根据标准化瞬时能量包络函数及离群值判断砂浆脱空将导致“误判”,即将未脱空处识别为脱空。当砂浆脱空长度为0.65、0.95、1.30和1.65 m时,标准化瞬时能量包络函数的离群值偏离幅度达109.80%、112.22%、125.06%和117.72%。与瞬时能量包络函数相比,标准化瞬时能量在砂浆脱空位置处幅值变化更加显著。
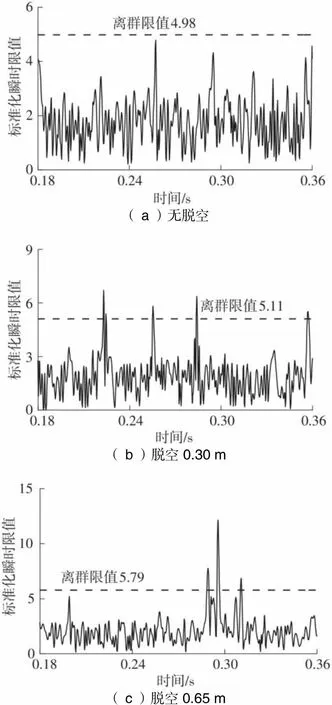
( a )无脱空 ( b )脱空0.30 m ( c )脱空0.65 m
综上所述,当瞬时能量和标准化瞬时能量包络函数均未出现离群值时,轨道不存在砂浆脱空;当包络函数出现离群值,且最大值较离群限值相差较大(瞬时能量和标准化瞬时能量幅值包络函数的离群值偏离幅度达50%和100%以上),则轨道出现较大长度(0.65 m及以上)砂浆脱空;当瞬时能量幅值包络函数未出现离群值,但标准化瞬时能量幅值包络函数出现离群值,则轨道可能出现较小长度(0.30 m及以下)砂浆脱空。
研究表明,砂浆脱空长度达到1.95 m时将对车辆运行安全性和轨道结构动力性能造成严重危害[3]。因此,尽管本研究提出的砂浆脱空识别方法仅在砂浆脱空长度不小于0.65 m时具有较高识别准确率,其仍然能够为工程检修提供参考依据,且不会影响行车安全和降低轨道使用寿命。
4 结论
本研究基于车辆-轨道耦合动力学理论建立仿真模型,得到不同砂浆脱空条件下的轮对垂向加速度。通过自适应滑动步长改进LMD算法,并分解轮对垂向加速度信号。依据峭度选取因砂浆脱空变化显著的1分量,并计算其瞬时能量和标准化瞬时能量增强砂浆脱空特征。最后利用1分量瞬时能量和标准化瞬时能量的包络函数及离群值确定砂浆脱空位置。结论如下:
(1)依据自适应滑动步长改进LMD算法,可将复杂非平稳轮对加速度分解为更少阶数分量,集中相同模态信息,衰减模态混叠现象。
(2)砂浆脱空信息主要包含在1分量中,且砂浆脱空长度越大,1及其瞬时能量和标准化瞬时能量在脱空处幅值越大。
(3)瞬时能量和标准化瞬时能量均可增强砂浆脱空特征,且标准化瞬时能量效果更为显著。
(4)当脱空长度为0.30 m时,瞬时能量包络函数未出现离群值,导致“漏判”;而标准化瞬时能量包络函数在脱空及未脱空位置处均有离群值,导致“误判”。当砂浆脱空长度不小于0.65 m时,瞬时能量和标准化瞬时能量幅值包络函数在脱空位置处均出现离群值,可用于确定砂浆脱空位置。
[1] YANG J,ZHU S,ZHAI W.A novel dynamics model for railway ballastless track with medium-thick slabs[J].Applied Mathematical Modelling,2020,78:907-931.
[2] REN J J,LI H L,CAI X P,et al.Viscoelastic deformation behavior of cement and emulsified asphalt mortar in China railway track system I prefabricated slab track[J].Journal of Zhejiang University-Science A,2020,21(4):304-316.
[3] WANG P,XU H,CHEN R.Effect of cement asphalt mortar debonding on dynamic properties of CRTS II slab ballastless track[J].Advances in Materials Science & Engineering,2014,2014:1-8.
[4] 胡志鹏,王平,熊震威,等.基于高斯曲率识别板式无砟轨道中CA砂浆脱空伤损[J].铁道科学与工程学报,2014,11(3):54-59.
HU Zhi-peng,WANG Ping,XIONG Zhen-wei,et al. The void damage identification of CA mortar in slab track based on the Gaussian curvature[J].Journal of Railway Science and Engineering,2014,11(3):54-59.
[5] 赵佳,谢铠泽,赵维刚,等.基于应变模态的CRTSⅡ型板式无砟轨道砂浆层脱空识别[J].北京交通大学学报,2020,44(4):57-64.
ZHAO Jia,XIE Kai-ze,ZHAO Wei-gang,et al.Identification of void in mortar layer of CRTS Ⅱslab ballastless track based on strain mode[J].Journal of Beijing Jiaotong University,2020,44(4):57-64.
[6] 胡琴,徐巍,高飞,等.基于BP神经网络的CRTSⅠ型板式无砟轨道CA充填层损伤识别[J].土木工程与管理学报,2018,35(5):87-93.
HU Qin,XU Wei,GAO Fei,et al.Damage identification of CA mortar layer of CRTS I slab trackbased on BP neural network[J].Journal of Civil Engineering and Management,2018,35(5):87-93.
[7] 田秀淑,杜彦良,赵维刚.基于瞬态冲击响应特性的无砟轨道砂浆层脱空的检测和识别[J].振动与冲击,2019,38(18):148-153.
TIAN Xiu-shu,DU Yan-liang,ZHAO Wei-gang.Detection and identification of mortar void in the ballastless track of high-speed railway based on transient impact characteristics[J].Journal of Vibration and Shock,2019,38(18):148-153.
[8] 陈甜甜,赵维刚,李荣喆,等.基于CNN的CA砂浆层脱空识别方法研究[J].铁道标准设计,2021,65(7):77-87.
CHEN Tian-tian,ZHAO Wei-gang,LI Rong-zhe,et al.Study on identification of CA mortar layer void based on convolution neural network[J].Railway Standard Design,2021,65(7):77-87.
[9] 陈梦. 高速铁路多层线下结构病害弹性波场无损检测方法研究[D].上海:上海交通大学,2014.
[10] 李再帏,吴刚,朱文发,等.基于Lamb波的CRTSⅡ型板式无砟轨道层间损伤检测方法[J].铁道学报,2020,42(12):120-126.
LI Zai-wei,WU Gang,ZHU Wen-fa,et al.CRTSⅡ slab ballastless track interlayer damage detection method based on Lamb wave[J].Journal of the China Railway Society,2020,42(12):120-126.
[11] 李自法,谢维波,刘涛.一种基于GBRT算法的CA砂浆脱空检测方法[J].铁道科学与工程学报,2018,15(2):292-301.
LI Zi-fa,XIE Wei-bo,LIU Tao.A detection method of CA mortar disengaging based on GBRT algorithm[J].Journal of Railway Science and Engineering,2018,15(2):292-301.
[12] SHI H,YU Z,SHI H,et al.Recognition algorithm for the disengagement of cement asphalt mortar based on dynamic responses of vehicles[J].Proceedings of the Institution of Mechanical Engineers Part F:Journal of Rail and Rapid Transit,2018,233:1-13.
[13] CAO H,FAN F,ZHOU K,et al. Wheel-bearing fault diagnosis of trains using empirical wavelet transform [J].Measurement,2016,82:439-449.
[14] SMITH J.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface,2005,2(5):443-454.
[15] CHENG J,YU D,YU Y.Application of support vector regression machines to the processing of end effects of Hilbert-Huang transform[J].Mechanical Systems & Signal Processing,2007,21(3):1197-1211.
[16] LIAN J,ZHUO L,WANG H,et al.Adaptive variational mode decomposition method for signal processing based on mode characteristic[J].Mechanical Systems & Signal Processing,2018,107(JUL.):53-77.
[17] SUN H,ZHANG X,WANG J.Online machining chatter forecast based on improved local mean decomposition[J].International Journal of Advanced Manufacturing Technology,2016,84(5):1045-1056.
[18] ZHANG Y,QIN Y,XING Z Y,et al.Roller bearing safety region estimation and state identification based on LMD-PCA-LSSVM[J].Measurement,2013,46(3):1315-1324.
[19] DENG L,ZHAO R.An improved spline-local mean decomposition and its application to vibration analysis of rotating machinery with rub-impact fault[J].Journal of Vibroengineering,2014,16(1):414-433.
[20] LI Y,XU M,ZHAO H,et al.A new rotating machinery fault diagnosis method based on improved local mean decomposition[J].Digital Signal Processing,2015,46(C):201-214.
[21] CHEN P,CHEN H G,CHEN W H.Improved ensemble local mean decomposition based on cubic trigonometric cardinal spline interpolation and its application for rotating machinery fault diagnosis[J].Advances in Mechanical Engineering,2020,12(7):1-19.
[22] JIA S,DHANASEKAR M.Detection of rail wheel flats using wavelet approaches[J].Structural Health Monitoring,2007,6(2):121-131.
[23] 辛欣,任尊松,李响. 高速轨道结构振动及传递特性[J].机械工程学报,2020,56(20):146-154.
XIN Xin,REN Zun-son,LI Xiang. Vibration characteristics and transmission of high-speed track structure[J].Journal of Mechanical Engineering,2020,56(20):146-154.
[24] 罗亭,马军,王晓东,等. 改进DLMD和TKEO的滚动轴承故障特征提取方法[J].电子学报,2021,49(2):387-393.
LUO Ting,MA Jun,WANG Xiao-dong,et al. Improved DLMD and TKEO method for fault feature extraction of rolling bearing[J].Acta Electronica Sinica,2021,49(2):387-393.
Mortar Void Identification Based on the Improved LMD with Dynamic Moving Step
XIN Xin REN Zunsong
(School of Mechanical,Electronic and Control Engineering,Beijing Jiaotong University,Beijing 100044,China)
As an important component of the ballastless slab track, cement asphalt mortar is prone to void damage under the combined action of high-frequency train loads and temperature loads. The mortar void can be located quickly and accurately according to the change characteristics of wheelset accelerations. The vertical wheelset acceleration was decomposed into a series of product functions via local mean decomposition improved by adaptive dynamic moving step. Based on the change of kurtosis, the first product function that can best reflect the mortar void characteristics was selected, and its instantaneous energy and standardized instantaneous energy were calculated to enhance the mortar void feature. By analyzing whether there are outliers in the envelope functions of instantaneous energy and standardized instantaneous energy, whether the mortar is damaged can be determined. The results show that when the mortar void length is no more than 0.30 m, there is no outlier in envelop function of instantaneous energy at the mortar void position, resulting in “missing judgment”; and the envelop function of standard instantaneous energy has outliers both at the void and non-void position, resulting in “misjudgment”. When the mortar void length is no less than 0.65 m, the envelope functions of instantaneous energy and standardized instantaneous energy only have outliers at the mortar void position, which can be directly used to locate the mortar void position. Identifying mortar void through responses of vehicle structures can effectively alleviate the pressure of track damage detection and improve vehicle operation efficiency.
ballastless slab track;mortar void;damage detection;signal processing
Supported by the Major Project of National Natural Science Foundation of China (11790281)
U213.244
1000-565X(2022)07-0098-10
10.12141/j.issn.1000-565X.210673
2021⁃10⁃25
国家自然科学基金重大项目(11790281)
辛欣(1993-),女,博士生,主要从事轨道车辆系统动力学及结构损伤识别研究。E-mail: 17116389@bjtu.edu.cn
任尊松(1969-),男,博士,教授,主要从事轨道车辆系统动力学及载荷谱研究。E-mail: zsren@bjtu.edu.cn

