斜拉索平行钢绞线控制张力的高精度无迭代求解

余贤宾 王荣辉 陈山亭 甄晓霞 张卓杰

斜拉索平行钢绞线控制张力的高精度无迭代求解

余贤宾1王荣辉1陈山亭2甄晓霞1张卓杰3，4†

（1. 华南理工大学 土木与交通学院，广东 广州 510640；2. 中铁大桥局集团第五工程有限公司，江西 九江 332001；3. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043；4. 河北省风工程和风能利用工程技术创新中心，河北 石家庄 050043）

为了高效地得到平行钢绞线斜拉索施工过程中各股钢绞线的控制张力的高精度解，研究了描述斜拉索静力状态的参数间的非线性关系，提出了各股钢绞线控制张力的高精度、无迭代求解方法。基于斜拉索悬链线索形精确解，采用泰勒展开求解了张拉完成时斜拉索无应力索长的高精度近似解；基于正装分析法和等值张拉法两个基本原则，推导了在平行钢绞线斜拉索施工过程中，张拉不同钢绞线时斜拉索的等效静力状态；通过对无应力索长、斜拉索等效截面积和斜拉索投影长度的近似处理，求解了各股钢绞线的控制张力的高精度解。以珠海市洪鹤大桥主桥（主跨500 m的叠合梁斜拉桥）、珠海市鸡啼门大桥（主跨210 m的预应力混凝土斜拉桥）及两篇文献中的斜拉索为算例，计算了本文方法的近似解与迭代求解的悬链线精确解之间的误差。结果表明：本研究提出的方法计算的斜拉索无应力索长与悬链线精确解的误差小于0.002%，各股钢绞线张拉力误差小于2%，完全满足现场施工的精度要求；本文方法精度高、计算代价小，具有极高的推广和应用价值。

平行钢绞线；斜拉索；控制张力；悬链线

平行钢绞线斜拉索具有便于运输和吊装、张拉设备吨位小、可分批次张拉、便于施工和更换、耐久性好、经济效益好等优点，已经在斜拉桥中获得普遍应用［1-2］。在平行钢绞线斜拉索的施工中，通常采用VSL（瑞士，威胜利）或者OVM（柳州，欧维姆）的“等值张拉法”进行施工控制［3-4］，要求满足均匀性和等效性原则。VSL法的张拉力值通过斜拉索悬链线理论的精确计算结果得到，计算精度高，但计算较为复杂；OVM等值法无需计算复杂的精确理论解，以控制后续张拉的钢绞线的张力与先施工的钢绞线张力相同来保证均匀性，计算简单但牺牲了一定计算精度。如何调和计算精度和计算量的关系，精确、简便地计算钢绞线的张拉力值是工程师和研究人员关心的重要问题。

为了得到平行钢绞线斜拉索施工过程中各股钢绞线的控制张力，研究人员进行了诸多尝试。例如基于“正装分析法”，从张拉第1股钢绞线开始递推张拉过程中各钢绞线的张力与索、塔、梁结构的变形协调关系，从而得到钢绞线张力的近似解［5-6］；或者假定前根钢绞线（一般为第1-2排）承担套管重量，其控制张力的大小根据拉索垂度由工程师结合经验确定，不需计算具体数值，而第+1根钢绞线则按照相应的等值法公式计算控制张力值［7］，在此基础上，考虑夹片回缩量、收缩徐变引起的索力变化值、拉索质量等对该公式进行完善［8］；此外，“等效串并联弹簧力学模型”［9］和采用“倒拆分析法”对各钢绞线的控制张力进行分析和求解的方法［10］也被提出；为了得到更高精度的解，有学者基于无应力状态法和斜拉索悬链线理论，采用Matlab程序［11-12］或者Excel VB程序［13］进行编程，迭代求解各股钢绞线的控制张力值；这些尝试均考虑了现场施工的实际需要，得到了各钢绞线控制张力的近似解或迭代解，其各有优势：近似方法计算公式简单、计算量小，但是不可避免地损失了一定的计算精度；迭代方法则正好相反，其计算精度高，但是计算较为繁琐，需要通过编程迭代程序求解，对计算人员要求较高。

本研究首先基于悬链线理论求解张拉完成时的斜拉索静力状态，采用泰勒展开求解无应力索长的近似解，随后从正装分析和等值张拉法两个基本原则出发，递推求解钢绞线施工过程中斜拉索的各静力参数之间的关系，利用已求得的悬链线理论无应力索长近似解，求解各股钢绞线的近似张拉力值。最后以珠海市洪鹤大桥、鸡啼门大桥以及两篇文献中的斜拉索为算例，计算了洪鹤大桥8#主塔边跨端20根斜拉索、鸡啼门大桥12#主塔中跨端16根斜拉索和文献算例［11-12］的无应力索长及各钢绞线的张拉力控制值。通过与悬链线精确解对比分析可知，使用本研究提出的方法计算的斜拉索无应力长度和钢绞线控制张力具有极高的精度，且计算不需要编制程序进行迭代求解，适用性好，具有很高的实用价值。

1　斜拉索的静力状态解

空间任意斜拉索可以通过坐标变换转换为平面索进行求解［11-12］，如图1所示，考虑斜拉索，斜拉索挂设完成后，塔端锚点点坐标位于坐标原点，梁端锚点点坐标为（，），即挂索后斜拉索的水平投影长度和竖直投影长度分别为和。斜拉索的自重线密度沿索长均布。在斜拉索中任取拉索微元，其长度为d，受力分析见图2。在分析中，做如下假定：

（1）斜拉索只能受拉，不能受压，且不考虑斜拉索的抗弯刚度；

（2）斜拉索处于弹性变形阶段，满足胡克定律；

（3）忽略变形引起的斜拉索截面变化。

对图2的索元进行受力分析，有：

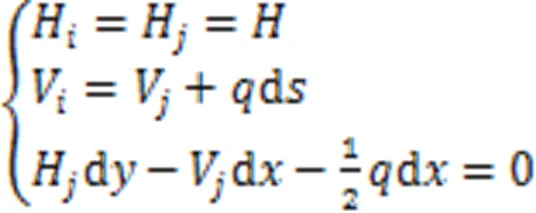
式中：Hi、Hj分别为拉索索力在i端、j端的水平分力，由于在分析中仅考虑了竖直方向的自重作用，因此拉索的水平分力沿索长为定值H。Vi、Vj分别为拉索索力在i端、j端的竖直分力，Ti、Tj分别为拉索微元在i端、j端索力值，为索上各点的竖直方向坐标。

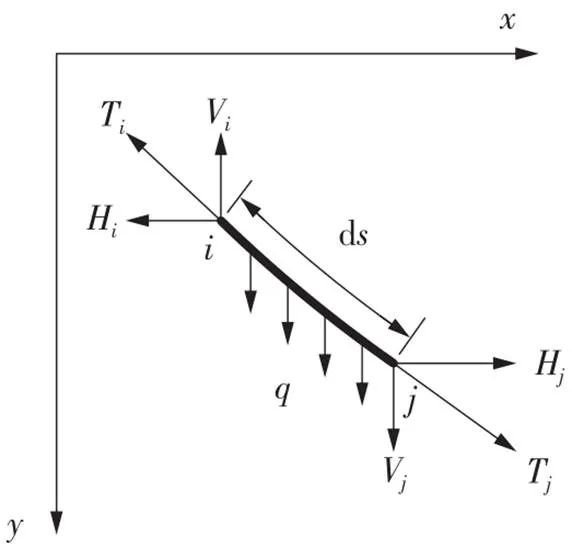
图2　斜拉索索元受力状态分析

由此，可以建立微元体的平衡微分方程：

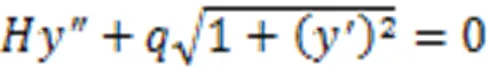
式中，1、2为任意常数。代入边界条件

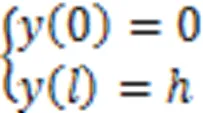
解得：

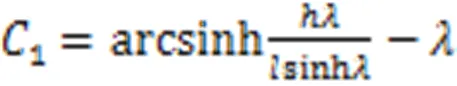
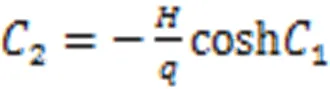
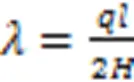
式中：为无量纲参数。斜拉索任一点的张力为

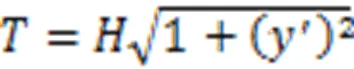
斜拉索的索长为

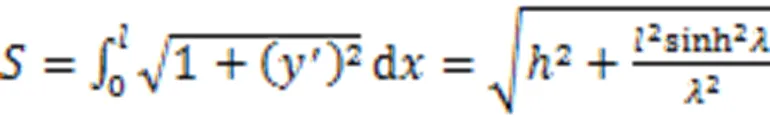
斜拉索的弹性伸长量为

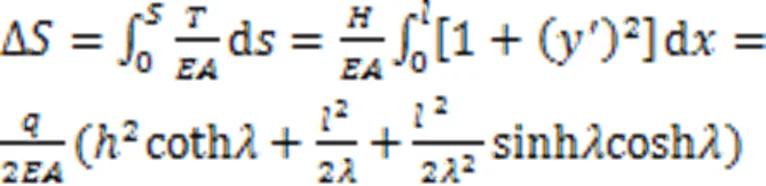
式中：为斜拉索的杨氏模量，为斜拉索的横截面面积。则无应力索长为

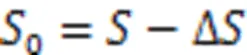
当已知张拉完成时斜拉索的几何参数及张力时，通过式（8）和式（11）可求得斜拉索的无应力索长；当已知几何参数及无应力索长0时，通过式（8）和式（11）可求得斜拉索的张力；由于式（8）和式（11）均是关于的超越方程，一般需要通过迭代求解。当为小量时，可以采用以下方法近似计算无应力索长［14-15］：

由式（8）可得，塔端索力

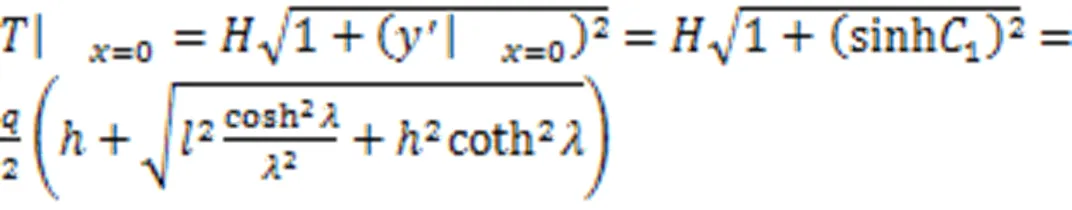
变形得

若为小量，则式中的双曲函数可展开为

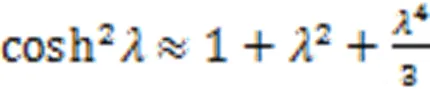
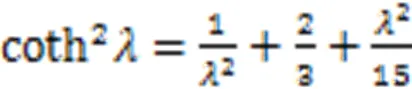
将上述两式代入式（13），略去的高次方项后，有

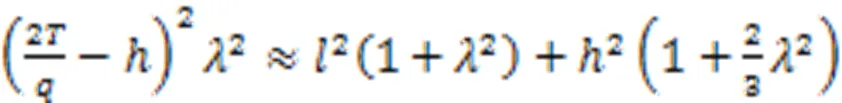
解得

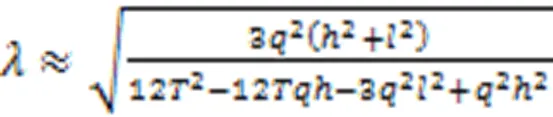
将式（17）计算得到的值代入式（9）-（11），即可求得无应力索长的近似解。

2　无迭代求解钢绞线控制张力

文献［11-12］给出了钢绞线张力的具体数值计算方法和迭代步骤，这些数值方法均是基于斜拉索静力状态的悬链线解，通过编程迭代求解，这里不再赘述。本研究提出一种无需迭代的高精度求解方法，具体介绍如下。

根据等值张拉法的两个基本原则，全部钢绞线张拉完成后，斜拉索中各股钢绞线具有完全相同的受力状态：各股钢绞线的张力、弹性伸长量和无应力索长均相等。显然，任意一股钢绞线从张拉开始，到最后一股钢绞线张拉完成，其无应力长度始终不变。因此，前述求解得到的无应力索长即为各股钢绞线的无应力长度的近似解。

在斜拉索的静力状态参数中，斜拉索的几何参数为斜拉索索形在水平和竖直方向的投影长度和，亦即塔、梁锚点连线在水平和竖直方向投影长度，而非斜拉索锚点的绝对空间坐标。因此为方便处理，在分析钢绞线张拉过程时，总是可以令图1中的坐标原点跟随塔端锚点变化，显然这对计算结果没有影响。

张拉第1股钢绞线前，塔、梁锚点的初始位置可由施工计算模型或者实际测量得知，假定锚点连线在水平和竖直方向的投影长度分别为0和0；张拉完第（1，2，…，）股钢绞线后，套管重量完全由这股钢绞线承担，此时斜拉索等效线密度为

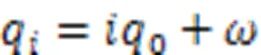
坐标原点处的斜拉索张力为

式中：t为第股钢绞线的控制张力。此时，斜拉索索形为：

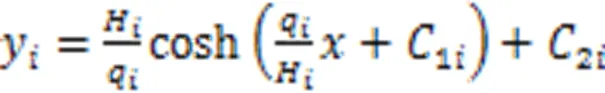
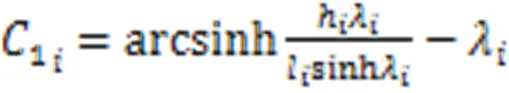
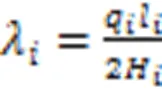
假设在斜拉索施工过程中，由于钢绞线张力作用，塔、梁锚点间距离变化量与斜拉索张力存在线性关系：

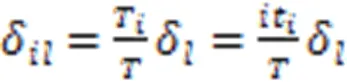
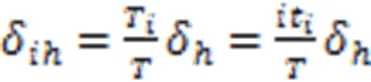
式中：δ、δ分别为张拉完股钢绞线时，塔、梁锚点连线在水平和竖直方向投影长度的累计变化量；δ、δ分别为张拉完全部钢绞线后，塔、梁锚点连线水平和竖直方向投影长度的累计变化量，可由施工计算模型得到。为斜拉索的目标索力，T为张拉完钢绞线时的斜拉索索力。

此时斜拉索水平方向和竖直方向的投影长度l和h分别为：

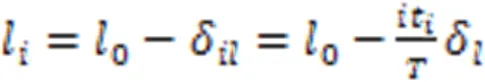
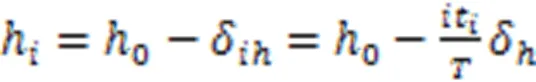
特别地，当时，为斜拉索的钢绞线股数，即当钢绞线全部张拉完成时，有：

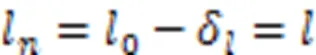
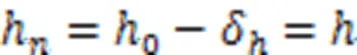
张拉完股钢绞线时斜拉索的索长为

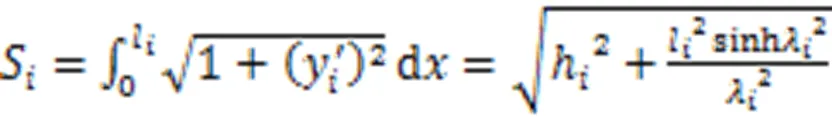
弹性伸长量为

式中：A为张拉完股钢绞线时斜拉索的等效截面积，T、H分别为张拉完股钢绞线时斜拉索的索力和水平分力。则此时的无应力索长为

注意：此时0可视为已知量，即可由式（9） - （11）、式（17）联立解得。

当λ为小量时，对式（30）-（31）进行近似处理［14］：

将式（33）-（34）代入式（32）得

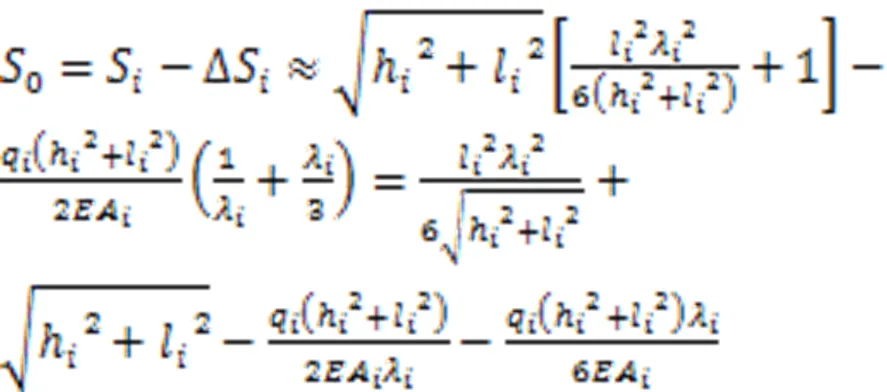
其中，

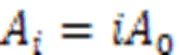
式中，A为斜拉索等效截面面积，0为单股钢绞线截面面积。

将式（35）整理即可得到关于λ的一元三次方程：

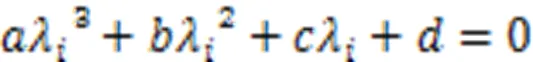
式中：

令

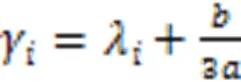
则原方程可化简为

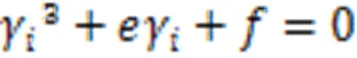
式中：

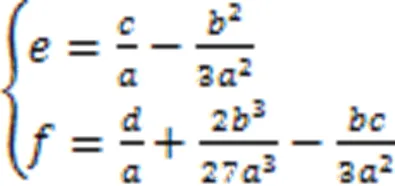
此一元三次方程的判别式为

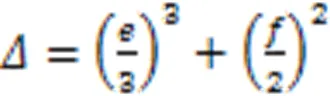
方程的实数解为

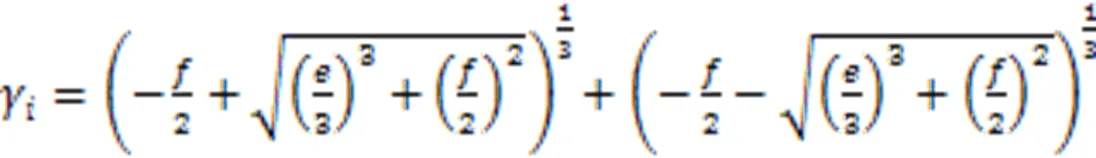
求解式（43）和式（39），即可求得λ的近似解，将其代入式（19），则可解得张拉完股钢绞线时斜拉索的张力T，则第股钢绞线控制张力为

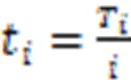
由以上推导可知，理论上可求解平行钢绞线斜拉索施工过程中的任一静力状态。然而，由式（26）-（27）可知，斜拉索在水平和竖直方向的投影长度是索力T（或t）的函数，将两式直接代入其他参数的计算公式中，无法将索力T（或t）与其他参数进行解耦，仍然需要通过迭代进行求解。因此，对锚点连线投影长度进行以下近似：

当1时，即只张拉完成第1股钢绞线时，令

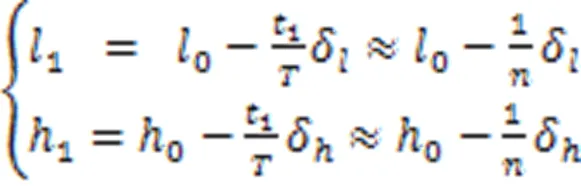
当1<≤时

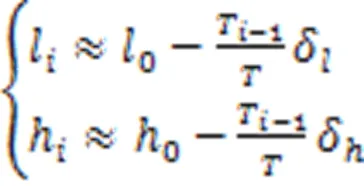
至此，在平行钢绞线斜拉索施工过程中，任意一股钢绞线的张力控制值可以无需迭代求解得到。

3　工程算例

根据以上推导公式，选取珠海市洪鹤大桥主桥磨刀门水道主航道桥（主跨500 m的双塔双索面叠合梁斜拉桥）8#主塔边跨端的20根斜拉索和鸡啼门大桥（主跨210 m的预应力混凝土斜拉桥）中跨端16根斜拉索（C1-C16），及文献［11］和文献［12］中的斜拉索为算例进行分析，采用本研究提出的方法和悬链线精确解，求解了各斜拉索在设计张拉力下的无应力索长。文献［11］和文献［12］中斜拉索算例的参数见表1，计算结果见表2和图3所示；分别采用本研究提出的无迭代方法和使用Matlab软件编程的迭代求解程序求解了各斜拉索任意一股钢绞线的控制张力和斜拉索的等效张拉力，各斜拉索张力的最大误差见图4和图5。任意选取了洪鹤大桥3根典型斜拉索（边跨1#短索、11#中索和20#长索），斜拉索参数见表3，其张拉过程中的几何参数l和h、各钢绞线控制张力t和斜拉索张力T的详细计算结果和误差情况如图6-图14所示；选取了鸡啼门大桥3根典型斜拉索（中跨1#短索、8#中索和16#长索），斜拉索参数见表4，其各股钢绞线控制张力t和斜拉索张力T的详细计算结果和误差情况见图15。其余斜拉索的详细计算结果限于篇幅此处省略。前述误差是指使用本研究提出的方法近似求解的值相对于编程迭代求解的悬链线法精确值的偏差。

表1　文献［11］和［12］中斜拉索的基本参数

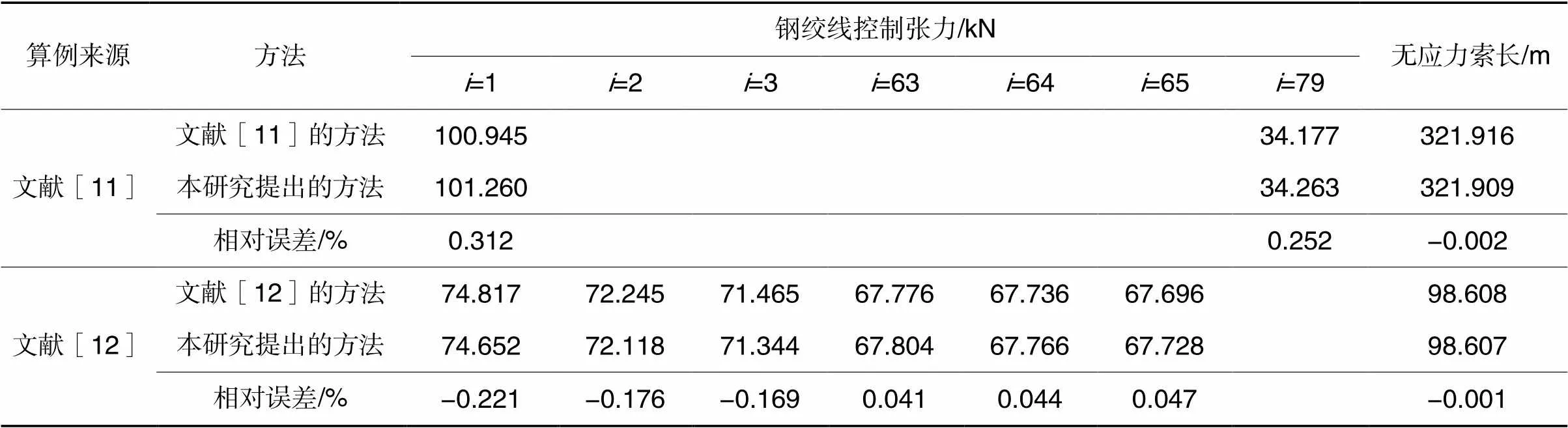
表2　文献［11］和［12］中斜拉索算例的计算结果对比

由表2和图3-图15的计算结果，可以得出以下结论：

（1）采用本研究提出的方法求解的文献［11］和文献［12］中的斜拉索算例，无应力索长的最大误差为7 mm，相对误差约为0.002%；求解的洪鹤大桥20根斜拉索的无应力索长误差均小于5 mm，相对误差约为0.002%，鸡啼门大桥16根斜拉索的无应力索长误差均小于0.05 mm，相对误差约为0.000 04%。计算结果说明无应力索长的计算精度很高，尤其对于鸡啼门大桥这种结构刚度大、拉索阶段结构变形很小的预应力混凝土斜拉桥，无应力索长的计算误差可以忽略不计。

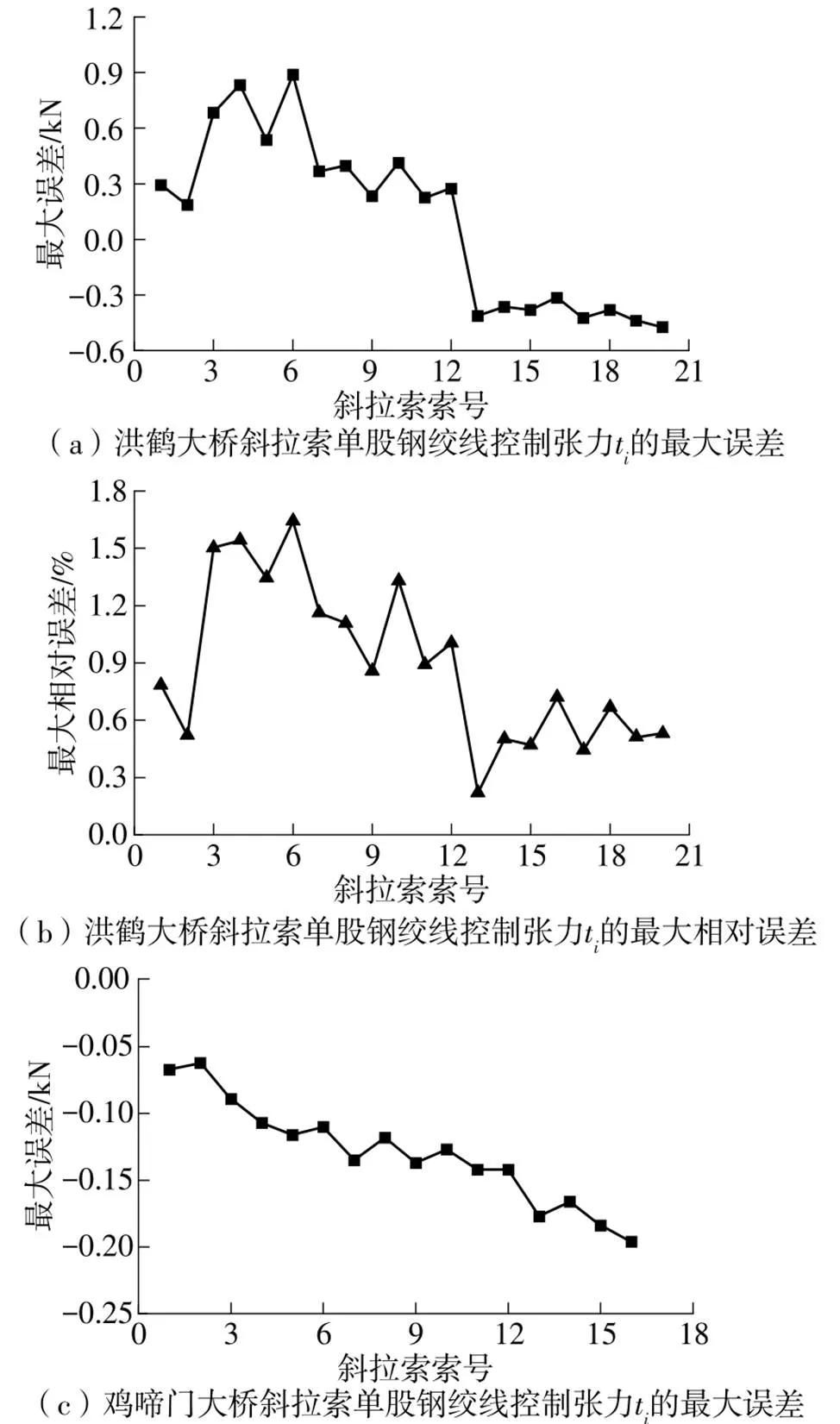
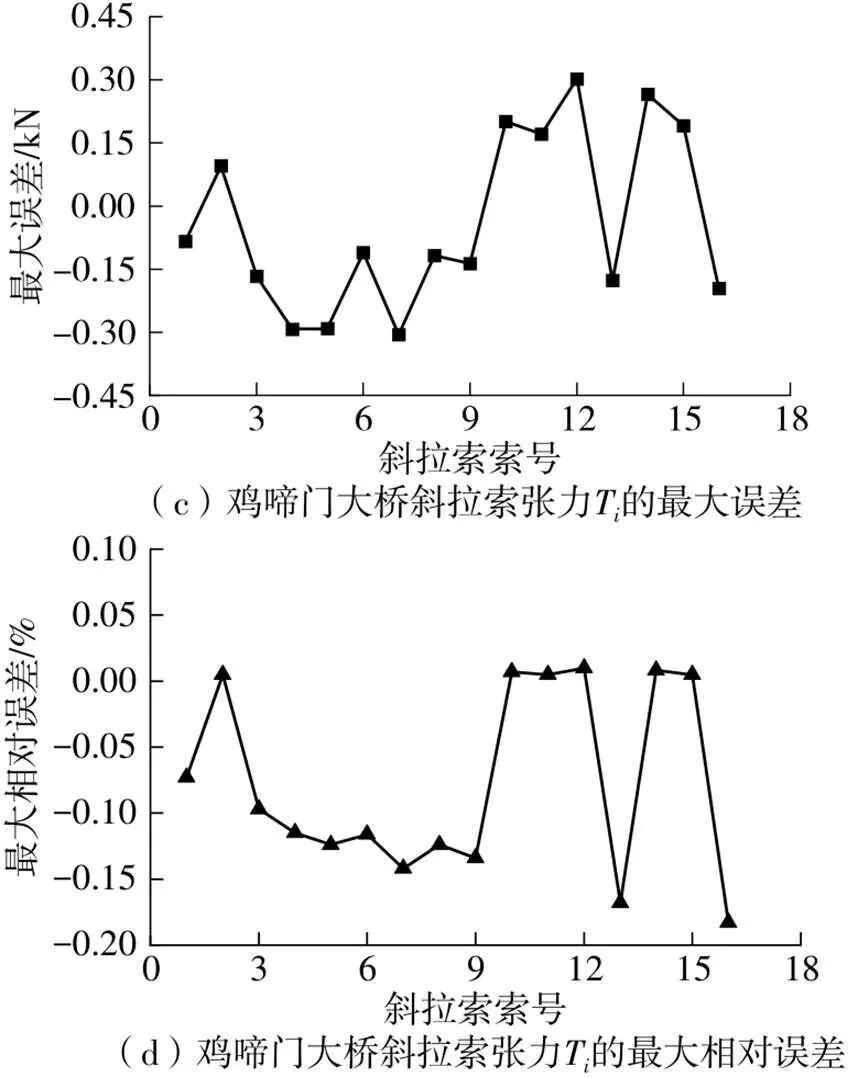
图5　洪鹤大桥和鸡啼门大桥斜拉索张力Ti的最大误差

（2）采用本研究提出的方法计算的文献［11］和文献［12］中的斜拉索算例，施工过程中的钢绞线控制张力t的最大误差为0.31 kN，相对误差约为0.31%；洪鹤大桥和鸡啼门大桥的钢绞线张力t的最大误差小于1 kN，斜拉索等效张力T的最大误差小于12 kN，相对误差均小于2%。

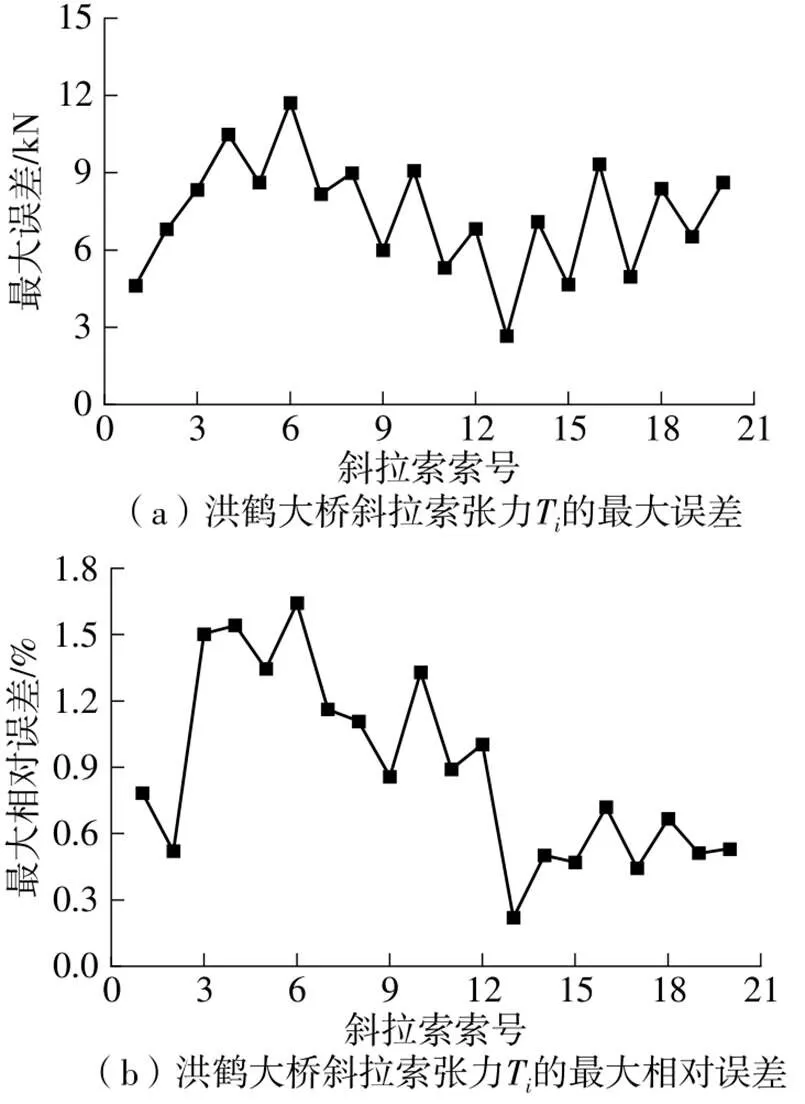
表3　洪鹤大桥不同长度斜拉索的基本参数

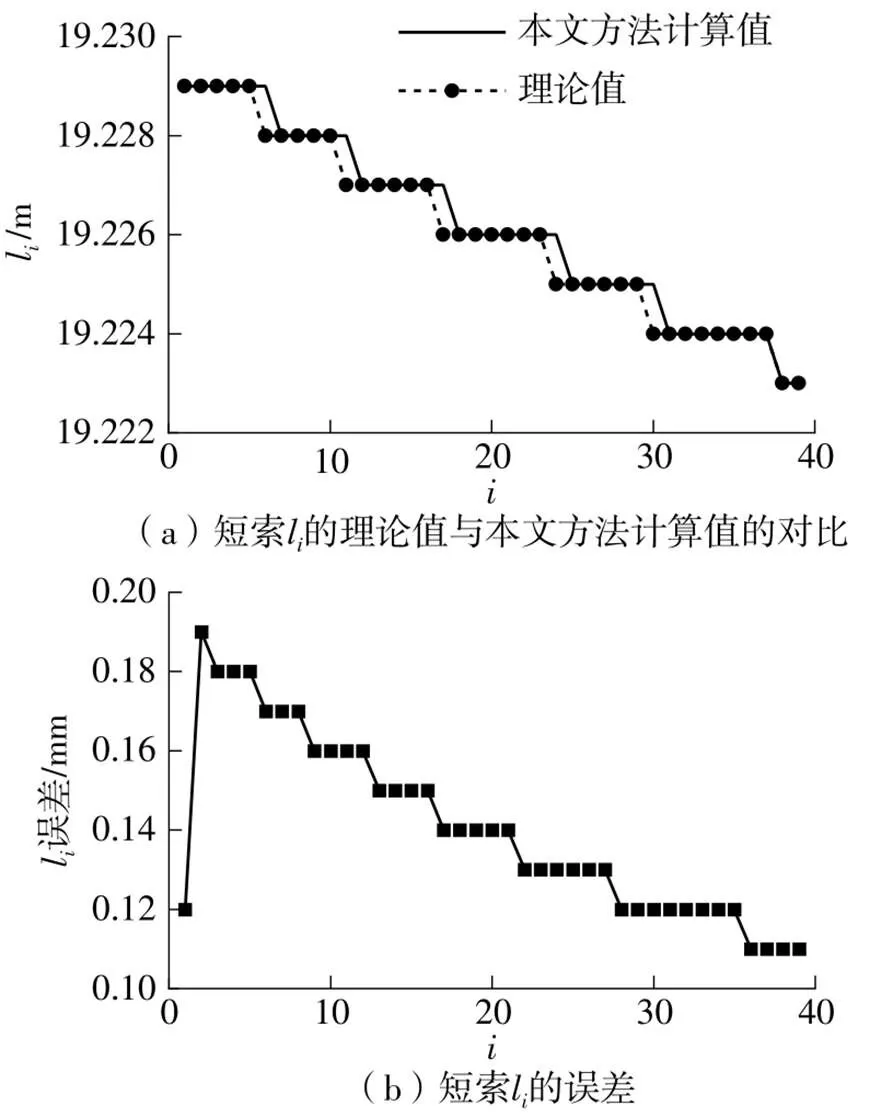
图7　洪鹤大桥短索li的计算结果

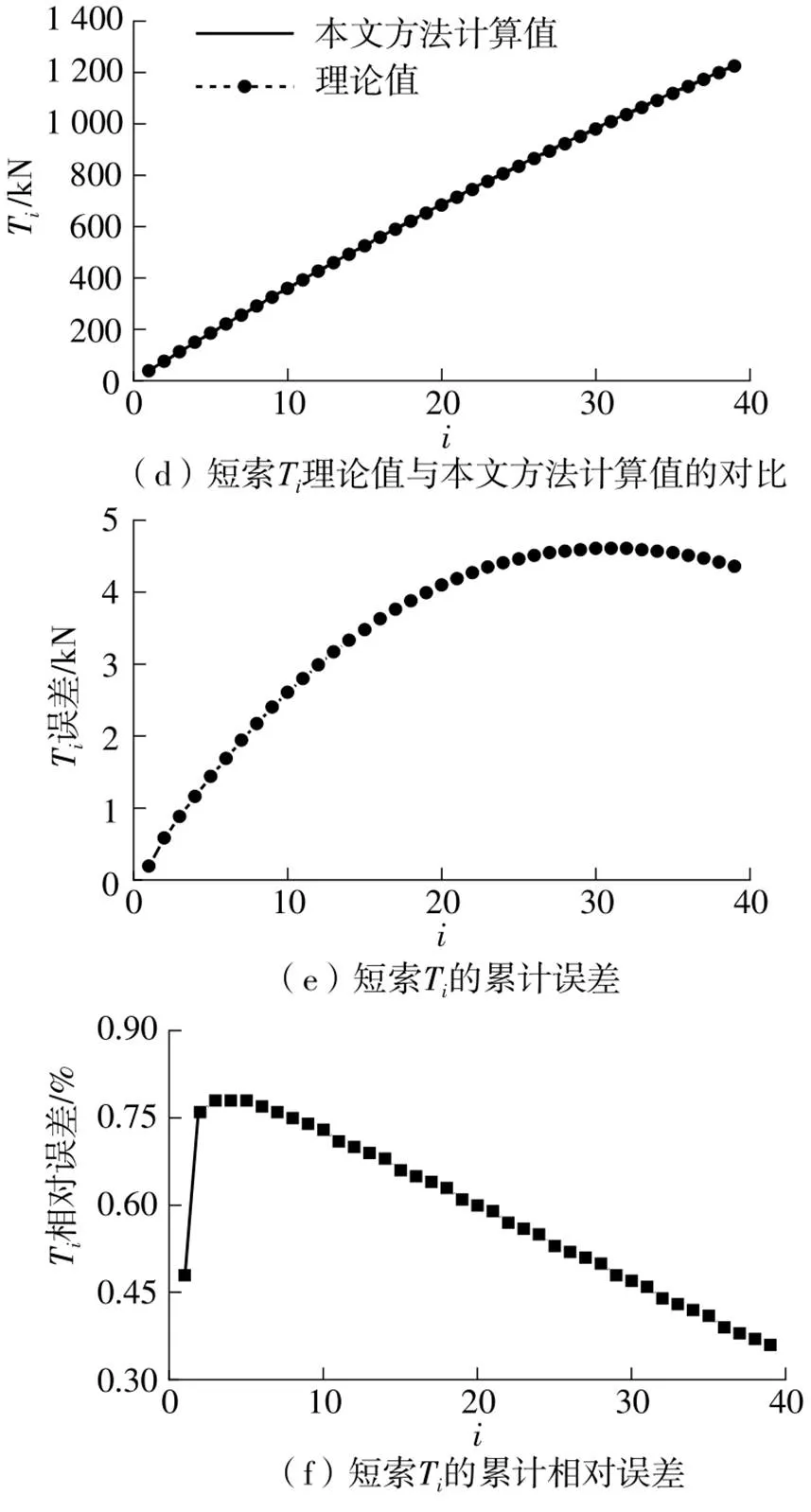
图8　洪鹤大桥短索的索力计算结果

图10　洪鹤大桥中索li的计算结果

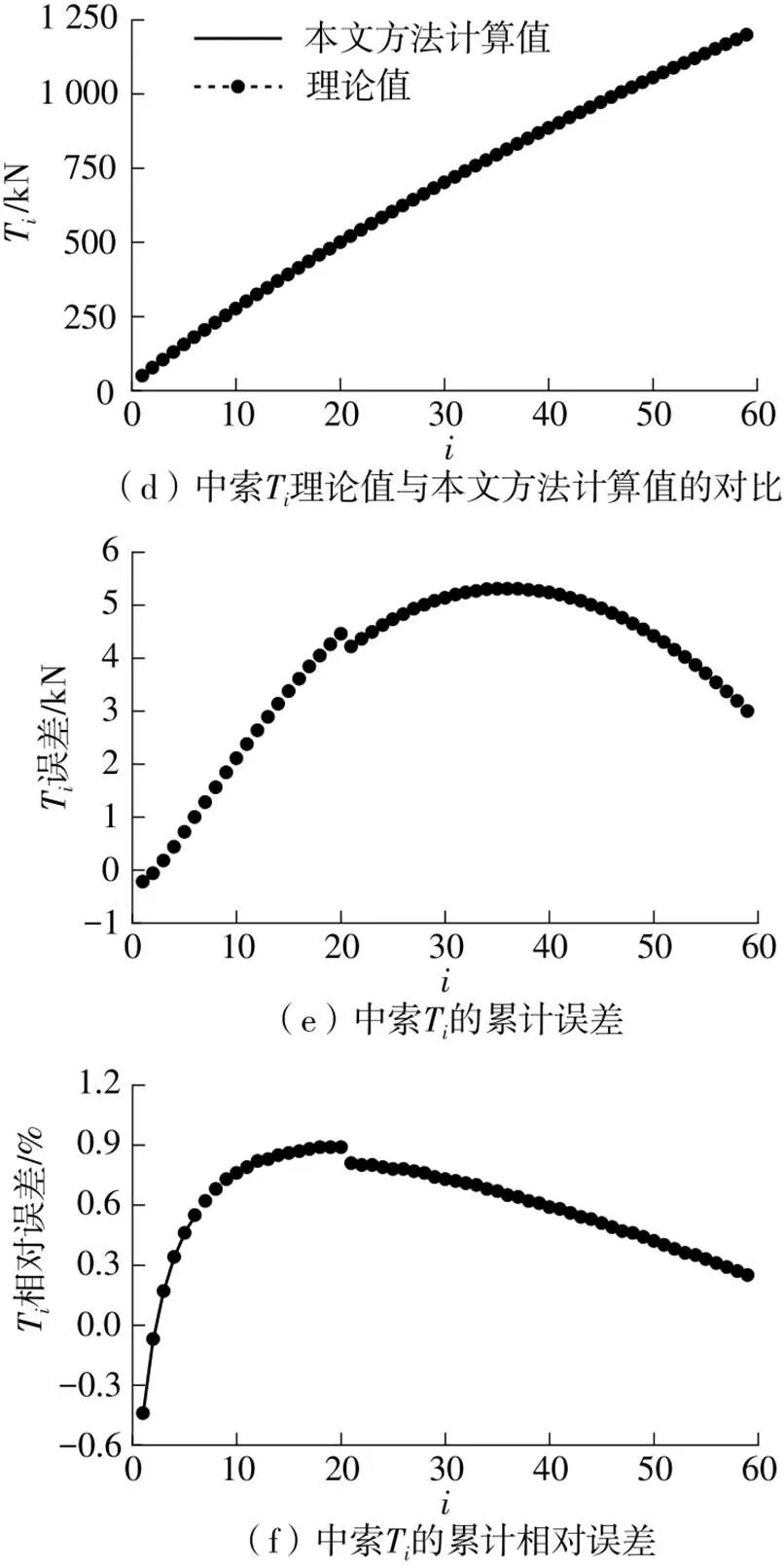
图11　洪鹤大桥中索索力计算结果

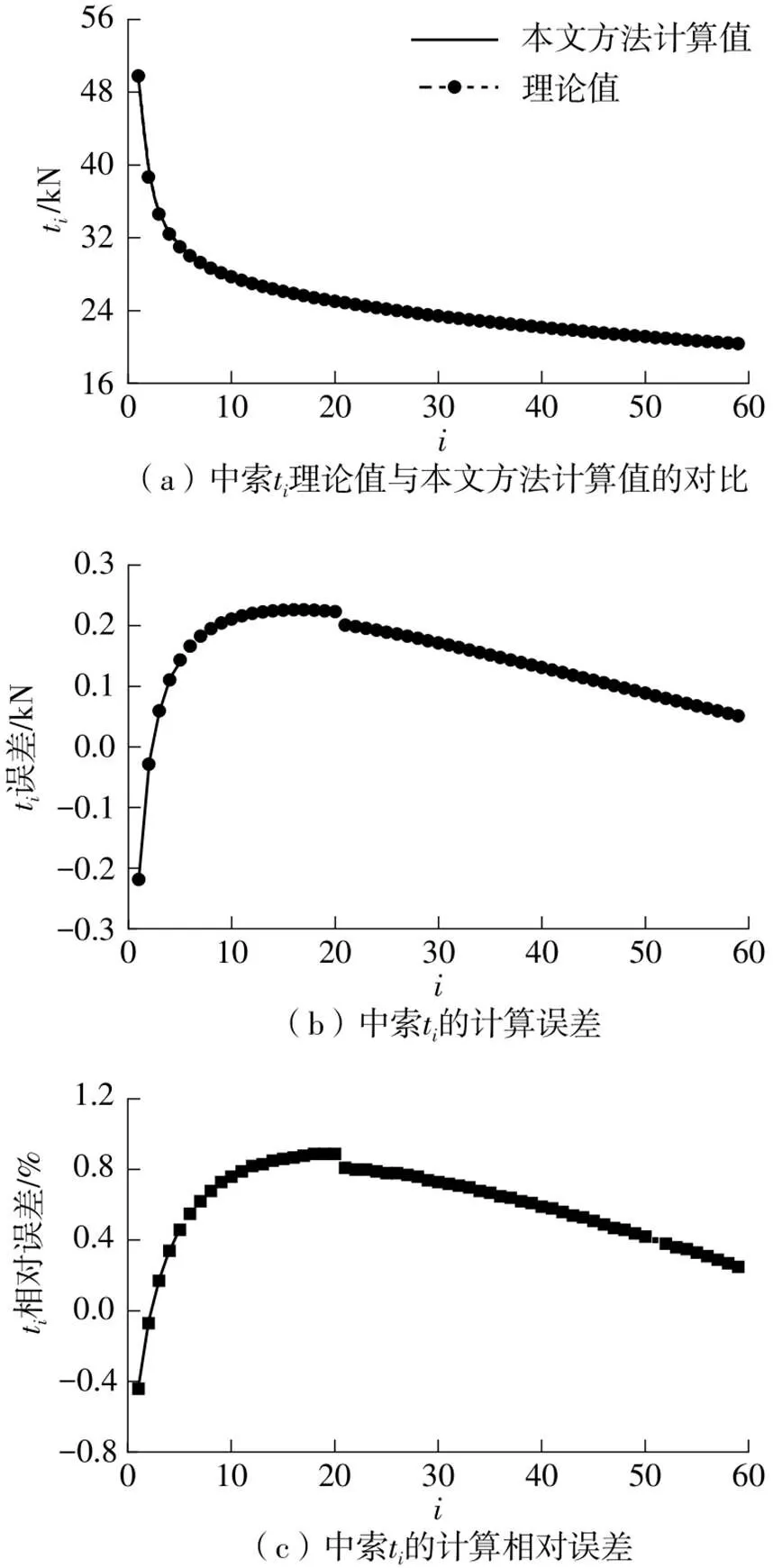
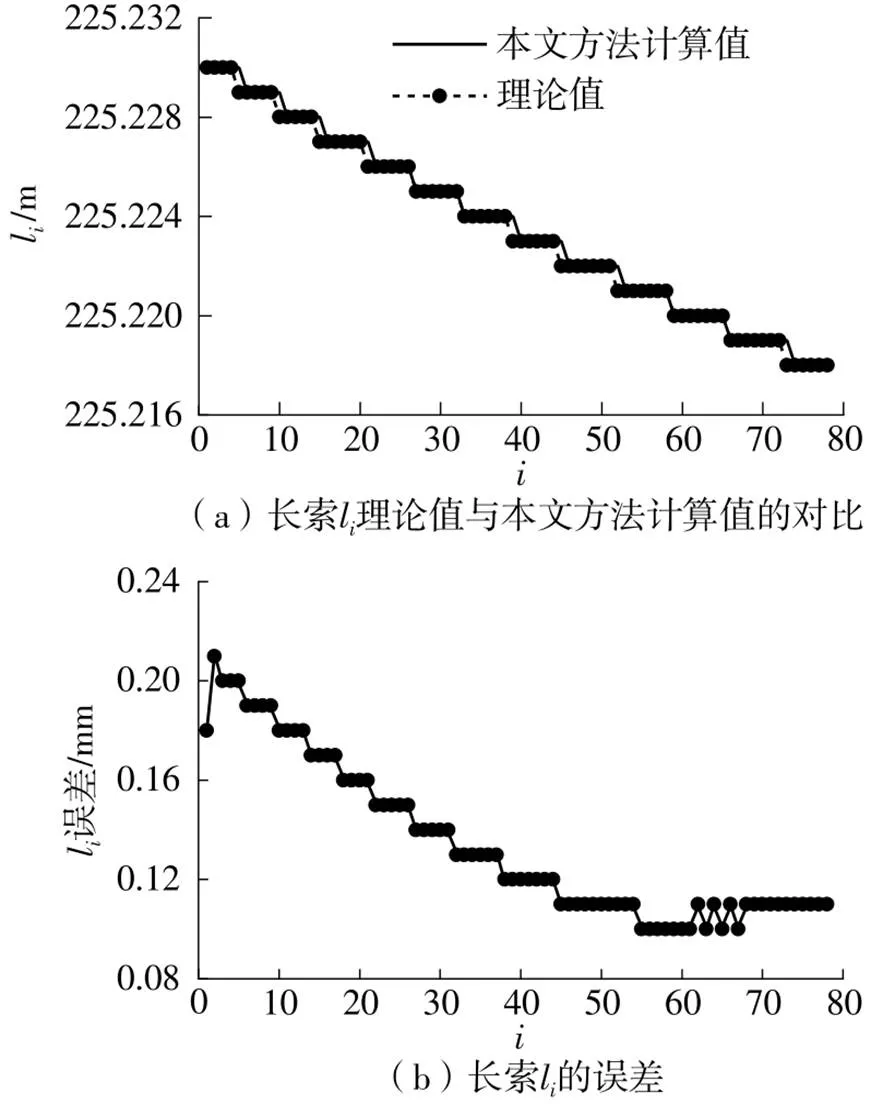
图13 洪鹤大桥长索li计算结果

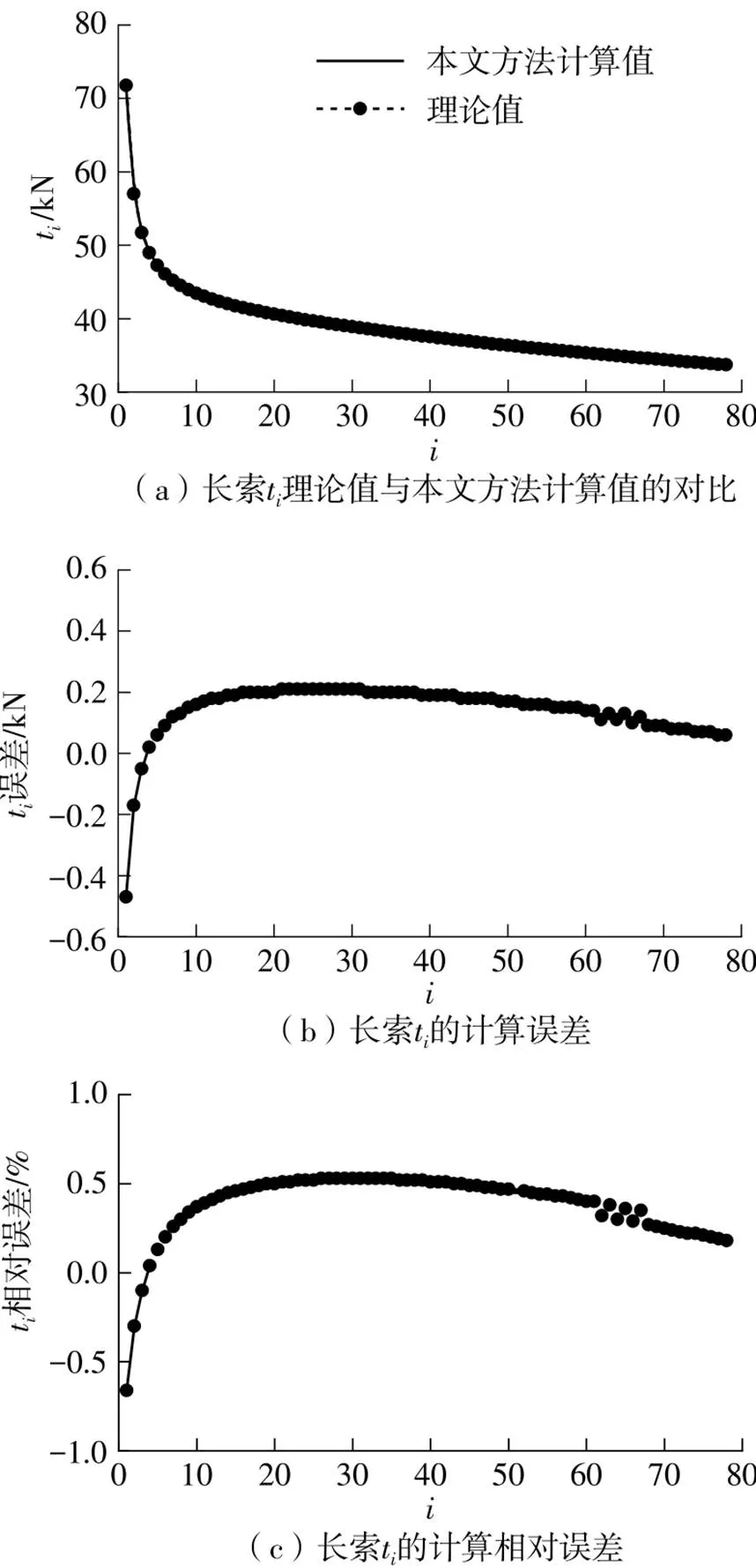
（3）斜拉索水平和竖直方向的投影长度h和l随着张拉股数的增加逐渐减小；本研究提出的方法计算的3根典型斜拉索的h误差均小于5 mm，l误差均小于0.23 mm，二者误差均随张拉股数的增加呈递减规律。

（4）斜拉索中各股钢绞线的张力t与钢绞线张拉股数间存在明显的非线性关系，原因是，在张拉开始，保护套管的质量就完全由已张拉的钢绞线承担，对于前几股钢绞线，套管质量相对于已张拉的钢绞线而言质量占比大，套管质量引起的非线性效应非常显著；当张拉的钢绞线超过10股后，套管的非线性影响减弱，各钢绞线的控制张力趋于以线性规律递减；在计算钢绞线张力时，套管引起的非线性影响不容忽视。

表4　鸡啼门大桥不同长度斜拉索的基本参数

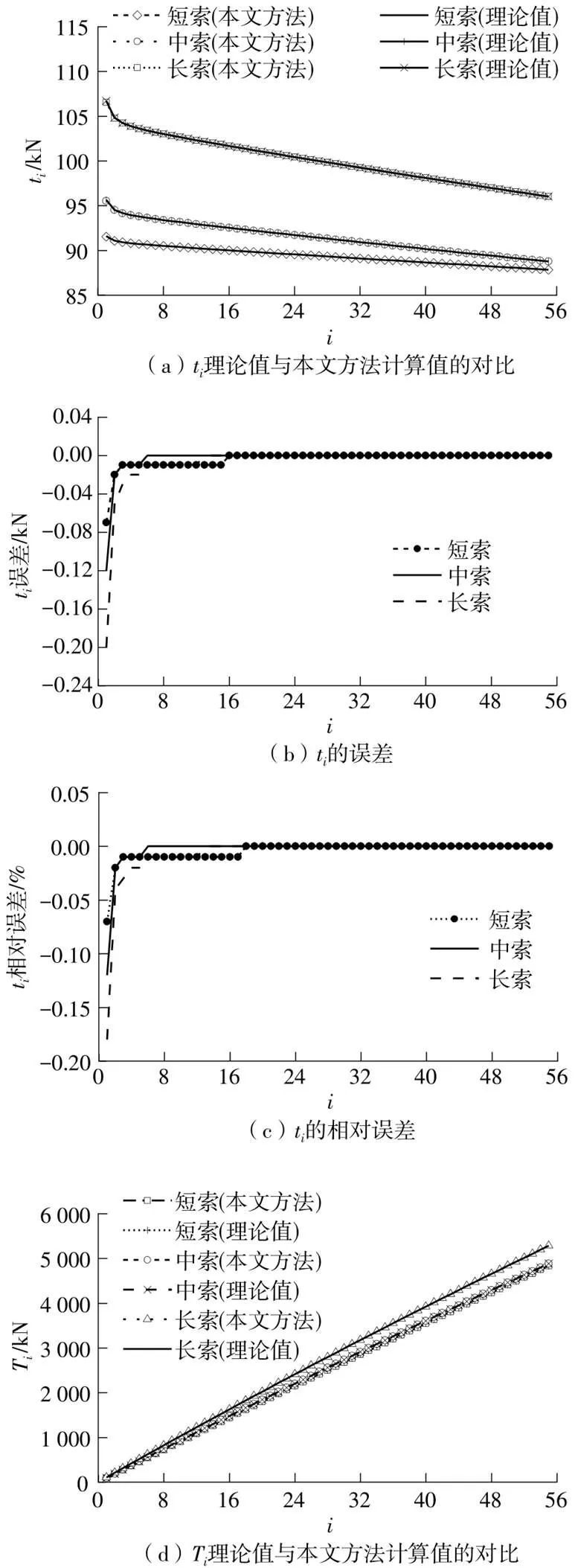
（5）在整个张拉过程中，斜拉索张力T随已张拉钢绞线股数呈近似线性增长。

（6）洪鹤大桥3根典型斜拉索各股钢绞线张力t与理论解的误差绝对值均小于0.5 kN，最后一股钢绞线的误差均小于0.2 kN；单股钢绞线误差及斜拉索张力累计误差均小于2%；鸡啼门大桥3根典型斜拉索各股钢绞线张力t与理论解的误差绝对值均小于0.25 kN，最后一股钢绞线的误差均小于0.1 kN，单股钢绞线张力t的误差及斜拉索等效张力T的误差均小于0.2%，说明本文方法计算得到的钢绞线的控制张力精度很高，完全满足现场施工的精度要求。

（7）本研究提出的方法不需要迭代，就可以求解等值张拉法钢绞线张拉控制力值，相比于现有的等值法计算方法，具有计算代价低、计算精度高的双重优点，具有很好的实用价值。

4　结语

在平行钢绞线斜拉索的施工过程中，通常已知斜拉索张拉前后的锚点位置、斜拉索的几何和质量参数、目标控制张力等，需要求解斜拉索的无应力索长和张拉过程中的任意一股钢绞线的控制张力。本研究提出了求解该问题的高精度、无需迭代的计算方法。

文中从基本的斜拉索悬链线索形及各静力参数间的关系出发，采用泰勒展开求解无量纲参数的高精度近似值，代入无应力索长的精确计算公式，避免了多处来源的误差，因此求解的无应力索长具有极高的精度；以悬链线解为基础，推导了张拉完任意股钢绞线时，斜拉索的等效静力状态；利用近似几何特征参数l、h和已求得的无应力索长0近似解，构造关于无量纲参数λ的一元三次方程，求解后代入张力T的精确求解公式，最终得到了斜拉索张拉过程中的钢绞线控制张力的高精度近似解。

从洪鹤大桥、鸡啼门大桥及参考文献中的斜拉索算例计算结果可知，本研究提出的方法与悬链线精确解的偏差均在2%内。这表明此无迭代方法具有计算精度高、计算代价小的优势，可供现场施工人员和研究人员在求解平行钢绞线斜拉索施工过程中的结构分析和控制张力问题中使用。

［1］ 祖祥胜，刘征宇，柏国清．钢绞线拉索与钢丝拉索体系的比较［J］．安徽建筑，2010，17（3）：26-28，41．

ZU Xiang-sheng，LIU Zheng-yu，Bai Guo-qing．Comparison of steel strand cable and steel wire cable system［J］．Anhui Architecture，2010，17（3）：26-28，41．

［2］ 杨吉新，喻桥，石旷，等．平行钢绞线和平行钢丝斜拉索对比分析［J］．工程与建设，2019，33（1）：38-40．

YANG Ji-xin，YU Qiao，SHI Kuang，et al．Comparison and analysis of parallel steel strand and parallel steel wire cable［J］．Engineering and Construction，2019，33（1）：38-40．

［3］ 威胜利工程有限公司（中国VSL）．VSL钢绞线斜拉索体系索力控制技术［C］∥2002年全国桥梁学术会议论文集．北京：人民交通出版社，2002：970-981．

［4］ 董春光．大跨度钢桁斜拉桥施工控制关键技术研究［D］．广州：华南理工大学，2014．

［5］ 张育智，李乔，唐亮．宜宾中坝金沙江大桥索力控制研究［J］．铁道标准设计，2005（8）：27-30．

ZHANG Yu-zhi，LI Qiao，TANG Liang．Research of cable force control of Zhongba Jinsha river bridge in Yibin［J］．Railway Standard Design，2005（8）：27-30．

［6］ 闫维明，张志，陈彦江，等．大跨度斜拉桥施工过程中的索力控制方法［J］．土木建筑与环境工程，2010，32（5）：130-134．

YAN Wei-ming，ZHANG Zhi，CHEN Yan-jiang，et al．Method of cable tension controlling in the long-span cable-stayed bridge construction［J］．Journal of Civil，Architectural & Environmental Engineering，2010，32（5）：130-134．

［7］ 冷雪浩，林乐强，黄伟东．平行钢绞线斜拉索单根钢绞线张拉过程中的索力控制［J］．北方交通，2008（1）：83-84．

LENG Xue-hao，LIN Le-qing，HUANG Wei-dong．Control of cable force in the process of stretching the single strand of parallel strand stayed-cable［J］．Northern Communications，2008（1）：83-84．

［8］ 邹力，彭旭民，位东升．平行钢绞线斜拉索等值张拉力精确计算方法［J］．重庆交通大学学报（自然科学版），2015，34（2）：7-9，44．

ZOU Li，PENG Xu-min，WEI Dong-sheng．Accurate calculation method of equal tensile force of parallel strand stayed-cable［J］．Journal of Chongqing Jiaotong University （Natural Science），2015，34（2）：7-9，44．

［9］ 周正茂，龚振球，王素娟．倒退分析法确定拉索中钢绞线的张拉力［J］．公路交通科技，2009，26（4）：73-77．

ZHOU Zheng-mao，GONG Zhen-qiu，WANG Su-juan．Tension control for strands in cables based on reverse analysis［J］．Journal of Highway and Transportation Research and Development，2009，26（4）：73-77．

［10］ 庄冬利，许骏，肖汝诚．分阶段单根张拉的平行钢绞线斜拉索张拉力简化计算方法的研究［C］∥第二十一届全国桥梁学术会议论文集（上册）．北京：人民交通出版社，2014：422-428．

［11］ 苑仁安，秦顺全．无应力状态法在钢绞线斜拉索施工中的应用［J］．桥梁建设，2012，42（3）：75-79．

YUAN Ren-an，QIN Shun-quan．Application of unstressed state method to construction of steel strand stay cable［J］．Bridge Construction，2012，42（3）：75-79．

［12］ 张卓杰，王荣辉．求解平行钢绞线斜拉索初张力的数值算法［J］．华南理工大学学报（自然科学版），2014，42（2）：88-95，102．

ZHANG Zhuo-jie，WANG Rong-hui．Numerical method of determining installation force for parallel strand cables［J］．Journal of South China University of Technology（Natural Science Edition），2014，42（2）：88-95，102．

［13］ 任明飞，袁波，王科．平行钢绞线斜拉索单股首次张拉力计算方法研究及ExcelVBA程序编制［J］．城市道桥与防洪，2016（8）：271-273，301，26．

REN Ming-fei，YUAN Bo，WANG Ke．Study on calculation method of initial single-strand tension force of parallel steel strand stay cable and ExcelVBA programming［J］．Urban Roads Bridges & Flood Control，2016（8）：271-273，301，26．

［14］ 陈太聪，马海涛，苏成．拉索静力状态的高精度无迭代求解方法研究［J］．工程力学，2013，30（3）：244-250．

CHEN Tai-cong，MA Hai-tao，SU Cheng．Study on high-accuracy and non-iteration methods for determining static status of a cable［J］．Engineering Mechanics，2013，30（3）：244-250．

［15］ GRADSHTEYN I S，RYZHIK I M．Table of integrals，series，and products［M］．8th ed．San Diego：Academic Press，2014：42-44．

High-Accuracy and Non-iteration Methods for Control Tension of Parallel-Strand Stay Cables

YU Xianbin1WANG Ronghui1CHEN Shanting2ZHEN Xiaoxia1ZHANG Zhuojie3，4

（1.School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510640，Guangdong，China； 2.The 5th Engineering Co.，Ltd.，MBEC，Jiujiang 332001，Jiangxi，China； 3.State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures，Shijiazhuang Tiedao University，Shijiazhuang 050043，Hebei，China； 4.Innovation Center for Wind Engineering and Wind Energy Technology of Hebei Province，Shijiazhuang 050043， Hebei，China）

In order to obtain the high-accuracy solution for control tension of each strand of stay-cables during construction, this paper studied the nonlinear relationships among the parameters describing the static state of cables and proposed a high-accuracy and non-iteration solving method for control tension of each steel strand. Based on the exact solution of the catenary of the cable shape, the high-precision and approximate solution of the stress-free length of the cable was solved by the Taylor expansion method. Based on the two basic principles of forward assembly analysis and equivalent tensioning method, the equivalent static state of steel strands during the construction process was obtained by recursive calculation when different steel strands were tensioned. The high-precision solution for the control tension of each steel strand was solved by approximating the unstressed cable length, the equivalent cross-sectional area and the projected length of the diagonal cable.Taking the stay-cables of the main bridge of the Honghe Bridge (a composite girder cable-stayed bridge with a main span of 500 meters) in Zhuhai city, the Jitimen Bridge (a prestressed concrete cable-stayed bridge with a main span of 210 meters) in Zhuhai city and cables mentioned in two literatures as examples, the error between the approximate solution of the method in this study and the exact solution of the catenary of iterative solution was calculated. The results show that the calculated error of the stress-free cable length between the method proposed in this paper and the catenary solution is less than 0.002%, and the tension error of each strand is less than 2%, which fully meet the accuracy requirements of construction. The method presented in this paper has the advantages of high precision and low calculation cost, so it has a high value of popularization and application.

parallel-strand；stay cable；control tension；catenary

Supported by the National Natural Science Foundation of China （52178138，51908382） and the Natural Science Foundation of Hebei Province （E2019210311）

U443.38

1000-565X（2022）07-0043-13

10.12141/j.issn.1000-565X.210730

2021-11-18

国家自然科学基金资助项目（52178138，51908382）；河北省自然科学基金资助项目（E2019210311）

余贤宾（1993-），男，博士生，主要从事大跨度桥梁结构理论研究。E-mail：ctxbyu@mail.scut.edu.cn

张卓杰（1986-），男，博士，主要从事大跨度桥梁结构理论研究。E-mail：stdzhangzhuojie@163.com