长江上游边滩作用下的河道最大冲刷深度

陈雅飞， 王平义*， 王梅力， 赵聪聪， 郑飞东

(1.重庆交通大学河海学院， 重庆 400074； 2.重庆交通大学国家内河航道整治工程研究中心， 重庆 400074； 3.重庆交通大学建筑与城市规划学院， 重庆 400074)

边滩改变了河道的水流边界条件，使得滩体附近尤其滩头与顺直段的边界处的水流更加复杂，是长江上游洄游性鱼类的理想生境，但给长江上游来往的船只航行带来不利影响，为此研究边滩附近的水流规律及冲刷特性对于维护长江上游黄金航道的安全以及鱼类生境保护具有指导意义。研究边滩及滩体附近的冲刷规律可以类比丁坝坝头以及堆积体的冲刷。沈淇等[1]以靖江边滩为例,根据该水域丰富的水沙及地形观测资料,分析了弯曲与分汊河型过渡段靖江边滩年内动态冲淤演变规律及其成因，研究发现靖江边滩上段河势稳定,中下段冲淤反复,边滩冲淤变化主要位于7.0～12.5 m范围；施骐等[2]利用室内概化模型试验,研究了顺直型河道交错边滩在不同水沙条件下演变的规律；陈坤等[3]研究发现梯级水库拦沙作用使长江上游河段年均推移质和悬移质较水库群建成前分别减少了87%和98.5%,水库群下游泥沙补给大幅度减小引发河床冲刷、粗化,河床表层床沙中值粒径较水库群建成前明显增大；戈国庆等[4]重点分析了工程整治后河道内流态、地形变化对航道冲淤的影响,对航道整治工程进行了评价；Kasvi等[5]分析了沙质河流弯曲河道边滩的形态变化和水力参数；Pandey等[6]研究开发了两种新颖的多层叠置概化框架,用于模拟均匀泥沙条件下丁坝附近的冲刷深度。

分析以上学者对于边滩河段的研究成果不难发现，他们大多研究的是长江中下游的砂质边滩，以淤积为主，而且对长江上游卵石推移质边滩的冲刷演变规律研究较少，只是统计研究卵石推移质边滩冲刷演变后的平面形态特征，并未真正对边滩河段的冲刷深度进行分析与验证，时间比尺与流速比尺等也未充分考虑，为此，现通过动床水槽试验，研究不同坡度边滩在清水冲刷作用下的冲刷深度变化规律，并且采用常见的丁坝冲刷深度公式、堆积体作用下的冲刷深度公式对实测结果进行对比验证，最后结合以上冲刷深度公式，充分考虑影响边滩附近水流特性的各种影响因子，拟合建立边滩附近顺直段的最大冲刷深度计算公式。

图1 试验水槽平面布置图Fig.1 Layout plan of test water tank

1 试验概况

1.1 试验水槽与仪器

图1为边滩试验水槽的平面布置图，水槽长28 m，宽3 m，高0.8 m，由16 m的稳水区、6 m的试验区和6 m的尾水区组成，本次试验主要选取顺直段的3个断面(d9、d10和d11)进行研究，其中d9断面为滩头与顺直段的边界，d10为滩体中心线的位置，d11为顺直段与滩尾段的边界，边壁及槽底为混凝土砂浆抹面，具有一定的糙率；边滩中心位于中心线处，水槽中铺设20 cm厚的沙床，卵石推移质中值粒径为1 mm，容重为2.65～2.75 kN/m3，非均匀系数ψ=1.768；水槽上游由进水口和进水池组成，进水口处设置矩形薄壁堰来稳定水流，进水池末端设置拦污网来拦截过滤水中肉眼可见的杂质，水槽下游通过尾门来调节水位，并设有沉砂池来减少水库中泥沙颗粒的淤积。

试验水槽中的流速采用挪威Nortek科学仪器公司研制的高精度声学多普勒点式流速仪Nortek ADV(Vectrino)测量，Vectrino为非接触式测量系统，测量精度高(±0.01 cm/s)、无需率定、操作简单等优点；动水试验后的地形采用重庆交通大学西南水运工程科学研究所研制的水工物理模型地形自动量测系统，该系统为非接触式测量，适用于测量退水完全后的干地形，能够实时显示冲刷后测量断面的地形。

1.2 试验滩体与工况

通过查阅长江上游四川宜宾至重庆段航道图(比例尺1∶15 000)，统计长江上游主要顺直边滩的特征参数，并参考王梅力等[7]对于长江上游宜宾至重庆主城区河段45个典型的弯道凸岸边滩和弯道过渡段边滩的平面形态特征分析，概化了此次试验的两种边滩。边滩根据其临水面坡度不同，将其编号为A和B,其余形态参数均相同，如滩体长度为6 m，宽度为1.5 m，高度为20 cm，平滩段长1 m等，ks为迎水面坡度，km为背水面坡度，kα为临水面坡度，L/B为滩体长宽比，B/H为宽高比，L/h为长高比，以及b/B为平滩段滩面宽与滩体宽之比。迎水面、背水面和临水面均为斜平面，滩头段与滩尾段均为平稳过渡的弧形面，滩体中间的顺直段由平面和斜平面构成，更加接近现实中的滩体形态构造。图2为两种边滩三视图。

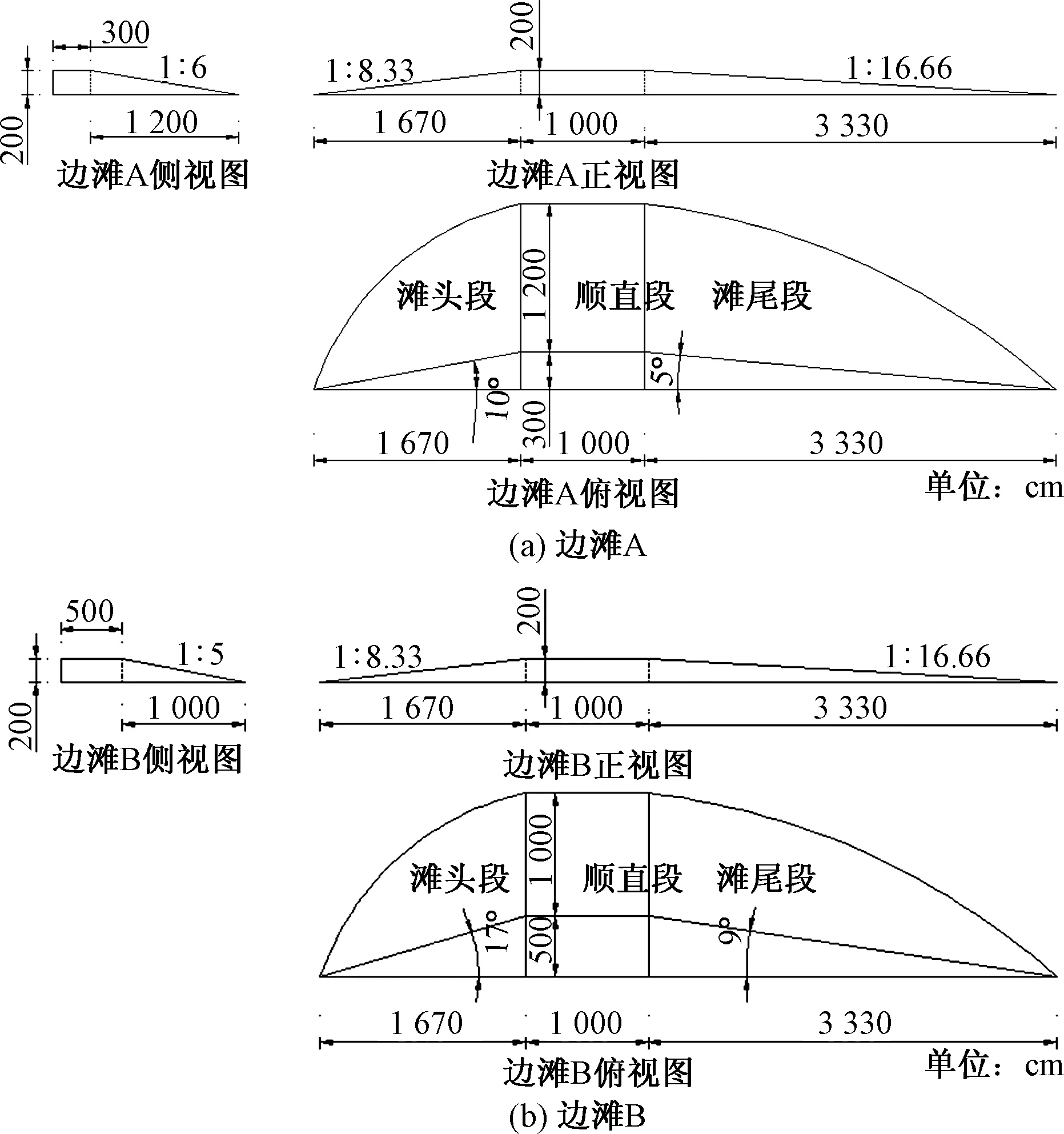
图2 两种边滩三视图Fig.2 Three views of two kinds of side beaches

为对比同一水深条件下不同流量对于滩体及周围河道的冲淤影响，分别采用3组流量90、120和150 L/s进行冲刷试验。试验水深均为15 cm，工况1～工况3以边滩A为研究对象，试验流量分别为90、120、150 L/s，工况4～工况6以边滩B为研究对象，试验流量分别为90、120、150 L/s。试验开始之前，先进行倒灌水，倒灌水的目的是减少开泵时由于水流的不平稳而造成的非有效冲刷，灌水持续时间约为2 h，直至水槽蓄水基本平稳后再开泵进行冲刷试验，此时尾门高度为最高，待开泵之后水流稳定时，将尾门缓慢调整至试验水深，左右两岸各布置若干个Gopro高清摄像机，对试验过程中的滩体冲刷进行实时跟踪，也有利于后期对冲刷图形的准确处理与分析。冲刷约6 h，待滩体及周围河道达到冲淤平衡后停止试验，关水后慢慢等待水槽中退水，以保证后期冲刷地形的完整性。

2 试验结果讨论与分析

2.1 边滩作用下顺直段河道冲刷深度

图3为顺直段主要断面冲淤变化图。横轴为距离边滩顺直段临水面边缘的距离，纵轴为实测的断面冲淤变化值，正值表示冲刷，负值代表淤积，断面冲淤变化的总体规律为：同一滩体的相同部位，水位等水力条件一定时，流量越大，冲刷深度越深；水深、流量等相同水力条件下，滩体临水面坡度越大，其水流结构更加复杂，绕流和水流之间的混掺现象更加明显，对应的冲刷深度也越大。以工况1和工况4为例，工况1的d10断面(滩体中心线)上最大冲刷深度为0.22 cm，冲刷位置距离纵向中心线30 cm;工况4的d10断面(滩体中心线)上最大冲刷深度为0.33 cm，冲刷位置位于纵向中心线上。曲线整体变化趋势为先升高后降低至逐渐平稳，不难看出最大冲刷位置并不都位于纵向中心线的位置上(如工况2和工况5、工况3和工况6)，而是随着流量的增加最大冲刷位置逐渐后移，工况2和工况5的最大冲刷位置距离纵向中心线30 cm，最大冲刷深度分别为0.65 cm和1.42 cm;工况3和工况6的最大冲刷位置距离纵向中心线40 cm，最大冲刷深度分别为2.47 cm和3.27 cm;主要原因是水流经过边滩顺直段时，河道过水面积减小，水流束窄并且发生绕流混掺现象，顺直段边缘处形成大小不一的漩涡，此时的流速不仅最大而且处于最为紊乱的状态，从而造成顺直段附近的冲刷，最大冲刷位置往往位于边滩顺直段纵向中心线的右侧区域，这一区域也与边滩流速分布图中的主流区相互对应。类比堆积体在不同流量下的流速分区图[7]绘制了图1的边滩水流分区图。

2.2 丁坝、堆积体公式的校核计算

选取具有代表性的丁坝冲刷深度公式和堆积体冲深公式，丁坝公式较多，选用文献[8]和文献[9]的公式，堆积体公式选用的是钱撼等[10]建立的堆积体附近局部平衡冲刷深度公式。表1为选用冲刷公式表。

将动床试验地形数据代入以上公式中，得到表2的各公式试算情况统计表。比较边滩顺直段实测地形数据与各个公式计算的冲深值，发现二者存在较大的误差。分析原因主要如下。

图3 不同滩体顺直段主要断面冲淤变化图Fig.3 Scouring and silting changes of main sections in straight sections of different beach bodies

表1 选用冲刷公式表

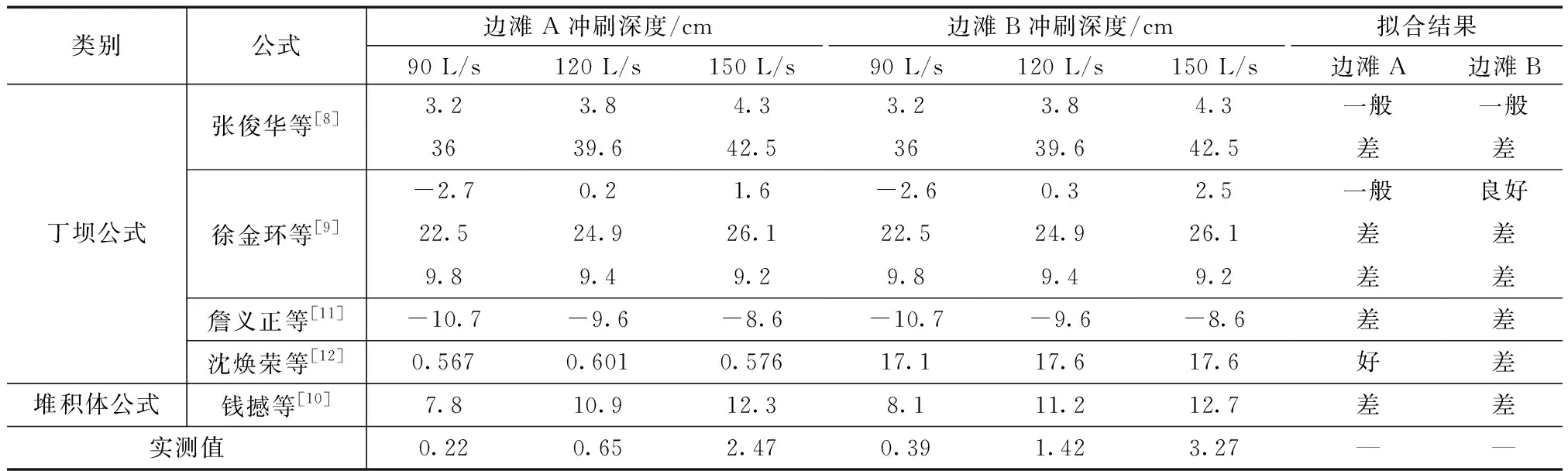
表2 各公式试算情况统计表Table 2 Statistics of trial calculation of each formula

(1)每个公式都是在特定的试验条件下完成和建立模拟出来的，具有唯一性。

(2)丁坝和堆积体与边滩相比，均属于小型的滩体，影响其附近的水流结构以及水流的复杂程度远远不如边滩，对于上游生态航道的影响较小。

(3)动水试验采用的是边滩概化模型试验，不能完全准确模拟现实航道中的边滩冲淤变化情况，而且选择的泥沙中值粒径为1 mm，对于动床试验而言属于卵石推移质，同样的水流条件下，卵石推移质颗粒起动相比悬移质的起动更为困难。

相比而言，沈焕荣等[10]建立模拟的丁坝公式对于边滩A而言拟合结果最好，主要原因是该公式在建立丁坝冲刷公式时充分考虑了丁坝冲深的影响因素，包括水流因素、床沙因素、几何边界条件等，并运用微积分等数学方法推导出丁坝局部冲深公式，更加科学准确；马卡维耶夫公式和航道整治规范公式的拟合结果较好，其他丁坝公式和堆积体公式的拟合效果较差，计算冲深为动床试验冲深的十倍甚至几十倍，考虑到在模型比尺的选择上存在较大差异，此次边滩动床冲刷试验模拟的是长江上游的卵石边滩，所以选择的模型比尺较大，卵石颗粒级配曲线如图4所示。

图4 试验泥沙颗粒级配曲线图Fig.4 Grain grading curve of test sediment

2.3 边滩冲刷坑公式的拟合

2.3.1 影响边滩顺直段冲刷深度的因素

金沙江梯级水库群的建立拦截了大量泥沙，水库下游河床长期受到清水冲刷的影响，所以此次动床冲刷试验以清水冲刷为主，综合考虑各种影响边滩顺直段冲刷深度因素，沈焕荣等[12]研究丁坝冲刷因素有水流因素、床沙因素和几何边界条件。为此，也可将边滩顺直段冲刷深度因素归纳如下。

(1)边滩结构对冲刷深度的影响，如滩体的坡度、滩体的长宽比、宽高比等特征因素。

(2)水力因子对冲刷深度的影响，如顺直段断面的平均流速和水深。

(3)床沙粒径选择对冲刷深度的影响，此次选择的床沙粒径中值粒径为1 mm，容重为2.65～2.75 t/m3，非均匀系数ψ=1.768。

(4)有效冲刷时间对冲刷深度的影响，令有效冲刷时间系数为t0/t。

参照王亚玲等[11]的分析思路，hs/h0与(V-Vs)/(V0-Vs)成正比，建立如下关系式。

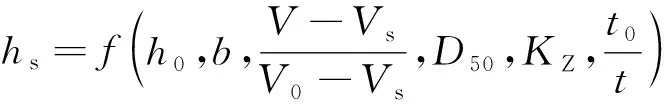
(1)

(2)

式中：h0为行近水深；V为边滩边缘的垂线平均流速(类比丁坝坝头流速)；V0为起动流速；Vs为起冲流速；D50为床沙中值粒径；b为边滩垂直流向的投影长度；ks、kn、kα分别边滩的迎水面坡度背水面坡度和临水面坡度。

2.3.2 边滩结构对冲刷深度的影响

查阅长江上游四川宜宾至重庆段航道图(比例尺1∶15 000)，归纳统计长江上游主要顺直边滩的形态参数，令KZ为边滩对于河道冲刷深度的影响系数，表3为不同边滩的特征因素表。

表3 不同边滩的特征因素表

2.3.3 水力因子对冲刷深度的影响

流速这一水力因子在边滩顺直段冲刷起到决定性作用，影响边滩水流结构的水力因子主要有沿着边滩顺直段边缘的垂向平均流速V、起动流速V0、起冲流速Vs、天然水深h和垂线平均流速弗劳德数Fr，根据测量得到的水深，验算各个工况下的起动流速V0，采用文献[9]的丁坝冲刷深度公式，即

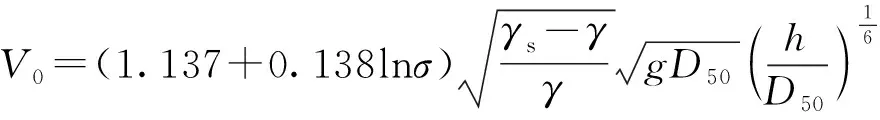
(3)

(4)

式(4)中：B为河宽，取3 m；H为边滩的高度，取20 cm；L为过水断面上的投影长度，取0.75 m和0.9 m。表4为各试验工况的流速汇总表，边滩顺直段边缘的垂向平均流速V大多大于起动流速V0，经过计算对比发现：边滩顺直段边缘的垂向平均流速V为边滩段河道平均流速的1.7～1.8倍，可见边滩顺直段位置的流速最大，垂线平均流速弗劳德数Fr均小于1。总体流速分布规律为：同一滩体，当水深、泥沙中值粒径等条件相同时，流量越大，边滩边缘垂线平均流速V越大，卵石推移质起动时对应的起动流速V0越大；不同坡度的滩体，当水深、流量等条件相同时，边滩B的边缘垂线平均流速大于边滩A的边缘垂线平均流速。

2.3.4 床沙粒径选择对冲刷深度的影响

关于床沙粒径选择对于丁坝等航道整治建筑物冲刷影响，国内外学者做了以下研究。王兆印等[14]通过各种泥沙大量实验，试验表明水力坡度等相同时，泥沙颗粒越大，上冲和下冲的效果越不明显；詹义正等[11]认为泥沙颗粒的粒径越大，其抵抗外界水流冲刷的能力越强，即当其他条件一定时，泥沙粒径越大，丁坝局部冲刷的深度会减小；Mwlville[15]通过清水冲刷和流速较小的动床试验，发现泥沙粒径越大，其平衡冲刷深度也越大。综上可知，泥沙粒径选择也是影响边滩顺直段冲刷的重要因素。

2.3.5 有效冲刷时间对冲刷深度的影响

不同学者对于丁坝、堆积体等的研究所选用的时间比尺以及流速比尺不同，经过以上计算校核后，大多数公式的计算结果也与边滩河段动水冲刷试验的地形实测值相差较大，张立等[16]讨论不同演变阶段冲刷坑边坡斜率与泥沙颗粒水下休止角大小关系时也引入有效时间的概念；喻涛等[17]研究非恒定流作用下丁坝局部冲刷时也考虑到有效洪水周期对冲刷坑范围及冲刷深度；胡杰龙[18]建立的丁坝坝头冲刷坑深度公式就充分考虑到坝头流速、护底结构长度以及有效冲刷时间等影响因素。结合以上学者的研究发现引入有效冲刷时间系数tk，tk十分必要，tk=t0/t，t0为有效冲刷时间，t为冲刷总时长，有效冲刷时间系数尤其用于动床试验研究观测冲刷后的地形变化，只有控制更多的可变水力影响因素，才能使得拟合出的公式更加符合工程实际。

2.3.6 冲刷深度公式的拟合

最大冲刷深度计算公式为

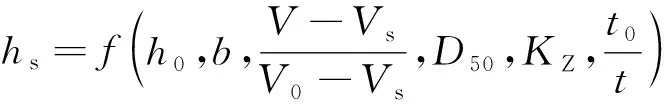
(5)

采用因次法，得到边滩顺直段附近平衡冲刷深度的无因次关系式为

(6)

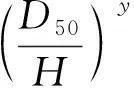
(7)

将实测的地形冲淤数据代入式(7)进行计算，当x=0时，等式左右两边成正比例关系，则

(8)

再次通过试验数据进行试算，解得z=0.214,tk=0.6，即ztk=0.128 4。

计算所得的冲刷深度hs与实测冲刷值最接近，所以推出边滩顺直段附近的冲刷平衡公式为

(9)

3 公式的对比验证

将动床试验冲刷的地形数据代入新拟合的冲刷公式中，计算结果较为理想，同时从上述丁坝公式中选择几个拟合较好的公式与新拟合的边滩顺直段冲刷深度公式进行对比，如图5所示，可见拟合公式更适用于边滩作用下顺直段附近的平衡冲刷深度计算。

表4 试验工况的流速汇总表

图5 各公式计算结果对比图Fig.5 Comparison of calculation results of various formulas

4 结论与讨论

通过动床冲刷试验，研究了不同滩体作用下的顺直段附近的冲刷深度，并采用丁坝冲深公式和堆积体冲深公式对试验数据进行计算与验证，最后充分考虑影响边滩顺直段附近的冲刷影响因素，补充有效冲刷时间比等因素，建立拟合了边滩顺直段冲刷平衡计算公式，主要结论如下。

(1)同一滩体的相同部位，水位等水力条件一定时，流量越大，冲刷深度越深；水深、流量等相同水力条件下，滩体临水面坡度越大，其水流结构更加复杂，绕流和水流之间的混掺现象更加明显，对应的冲刷深度也越大。

(2)丁坝冲深公式和堆积体冲深公式对试验数据进行计算与验证的结果与实测值相差较大，主要原因是边滩顺直段的水流结构更为复杂，绕流混掺等现象更加明显，而且实验时泥沙颗粒的选择以及有效冲刷时间均对于冲刷地形有重要影响。

(3)新拟合的边滩作用下顺直段附近的平衡冲深公式对于实测数据的拟合效果较为理想，可应用于长江上游卵石边滩顺直段的冲刷研究。

近底流速与卵石推移质滚动、跳跃的行为联系更加紧密，但由于滩体在清水冲刷作用下河床及滩体形态在发生变化，无法准确测量河床的近底流速，所以采用垂向平均流速进行计算;试验仅仅研究同一水深不同流量下的不同滩体冲刷规律，今后对于不同水深下的边滩顺直段以及滩头的冲刷仍需要继续研究。