成都市臭氧生成对气象因素的敏感性分析

侯梦琪，明镇洋，付 虹，李 迪，刘岳军

（西南交通大学地球科学与环境工程学院，成都 611756）

氮氧化物（NOx）是臭氧（O3）生成的根本，挥发性有机物（VOCs）是O3浓度升高的增长剂，气象因子是O3生成的基本条件，量化气象因子对O3生成的影响是研究O3生成机理的重要内容。KOVACANDRIC 等[1]采用傅里叶分析、主成分分析（PCA）以及多元线性回归分析等方法研究了克罗地亚东部气象变化与O3浓度的关系，结果表明，温度、太阳辐射时间、能见度和压力有利于O3的形成，相对湿度和云量降低了O3浓度。DAWSON等[2]基于CMAx模型，模拟分析了O3浓度对美国东部地区气象因子的敏感性，研究结果表明，温度对O3影响最大，温度每升高1 K，O3浓度升高0.73 μg/m3；绝对湿度对该指标的影响较小但显著；风速、混合层高度、云液态水含量和光学厚度对该指标的影响极小；对于超标日浓度而言，温度的影响最大，其次为风速和混合层高度。杨成江等[3]对吉林省O3污染与气象要素关系的研究表明，吉林省O3平均浓度随气压升高先增后减，与气温指标呈正相关。张磊[4]分析了气象要素对辽中地区O3的影响，发现太阳辐射和紫外辐射是影响辽中地区O3的主要气象因素。王玫等[5]利用相关系数分析了2014—2017年京津冀地区13 座城市O3与气象因子的相关性，指出冬季影响京津冀地区O3浓度变化的主要因素是相对湿度与风速，其他季节气温是主要因素。胡成媛等[6]利用2015—2016年四川盆地18个城市的国控站点监测数据及气象台站数据，采用广义加性模型（GAM）对影响四川盆地O3污染的主要气象因子进行识别，结果表明，臭氧与各气象因子均呈非线性关系，日照时数、相对湿度和气温是影响四川盆地O3浓度的主要气象因子。李英杰等[7]对成都中心城区O3浓度与各个气象要素进行研究，结果表明，成都中心城区近地面产生高浓度O3的主要气象因素为高温度、较低湿度、高边界层、无降水以及偏南风。由此可见，不同地区气象要素对O3污染的影响存在差异。

为了更加准确地揭示气象因子对成都市O3的影响程度，有必要建立可靠的臭氧预测模型，针对O3对各气象因子的敏感性，确定影响成都市O3的主要气象因子序列。本文利用2015—2019年成都市西南交通大学站污染物浓度监测数据、同期气象监测数据以及探空资料，构建BP 神经网络臭氧预测模型，之后采用全局敏感性分析方法，分别研究成都市O3浓度对上述气象因子的敏感度，以此确定影响成都市O3浓度的主要气象因子。

1 数据来源与方法

1.1 数据来源

本文所使用的O3-1 h 浓度数据及气象监测数据来源于四川省环境空气质量综合监测站，该站点位于成都市金牛区西南交通大学九里校区土木工程学院楼顶。气象监测数据内容包括太阳辐射（W/m2）、相对湿度（%）、温度（℃）、气压（hPa）、风向（°）和风速（m/s）。混合层高度（m）数据利用探空数据计算得到，其中探空资料来源于成都温江探空站（站点编号56187）。时间为2016年1月1日至2019年12月31日。本研究已参照《环境空气质量标准》（GB 3095—2012）的规定，对数据进行筛选和剔除，数据有效性满足要求。

1.2 臭氧浓度的BP 神经网络模型

1.2.1 模型建立方法

本文基于2016—2018年气象数据及O3浓度监测数据，采用后向传播（BP）神经网络模型构建臭氧浓度预测模型。网络初始化是构建BP 神经网络模型的先决条件，可直接影响模型的准确性。网络输入层、输出层和隐含层节点数、各层之间的连接权重值、学习率以及最大迭代次数等参数均需要在初始化过程中设置和选定。网络输入层节点数n由输入参数的个数决定，输出层节点数m则取决于输出参数的个数。由于本文拟构建利用温度、相对湿度、大气压力、太阳辐射强度、混合层高度、风速等气象因子预测臭氧浓度的神经网络模型，因此本文将输入层节点数n设置为6。输出数据为臭氧浓度，即本研究中输出层节点数m设置为1。

本研究首先参照经验公式计算隐含层节点数范围，再通过多次调试对比，得出最合适的隐含层节点数。节点数范围参考式（1）确定。

式中：l为隐含层节点数；a为（0，10）区间内的常数[8]。

由计算可知，隐含层节点数应在一定范围内选取[3]，经模型多次调试比较后，最终确定将隐含层节点数设置为4。

迭代次数影响隐含层节点的调整和权重值的更新。经多次测试比较，最终采用的学习率为0.001，最大迭代次数为20 000 次。选用ReLU 函数作为BP神经网络模型的激活函数f(z)，并以此对数据进行非线性处理。选用均方差函数作为BP 神经网络模型的损失函数，以此表征模型输出与期望输出的误差大小。

1.2.2 模型评估方法

利用标准化平均偏差（NMB）、标准化平均误差（NME）以及相关系数（R）等指标来验证神经网络模型的可靠性。NMB和NME表示模型输出值和观测值的偏离程度，其绝对值越小表明模型输出值越接近观测值；R用于表征模型输出值和观测值的接近程度，其值越接近1，表明模型输出值与观测值越接近。

1.3 敏感性分析方法

敏感性分析是研究模型各个输入参数对模型输出的影响程度[9-10]，通过对模型进行敏感性分析，对模型输入参数进行敏感性排序，可以确定影响模型输出的关键参数。目前，敏感性分析在生物学模型和水文水质模型等方面的应用已较为广泛[11-13]。敏感性分析主要分为局部敏感性分析和全局敏感性分析两类，其中，局部敏感性分析忽略了各输入参数的相互作用，不适用于非线性模型，且无法计算高阶敏感性。全局敏感性分析可以研究多个输入参数同时变化对模型输出的影响，克服了局部敏感性分析的缺点。常见的全局敏感性分析方法包括回归分析法、Morris 筛选法、Sobol 法、傅里叶振幅敏感性分析法（FAST）和区域敏感性分析法（RSA）等。

Sobol 法是一种基于方差的分析方法，以输入参数对模型输出方差的贡献比例衡量参数敏感性[14]，适用于非线性模型，计算结果稳定可靠，目前已在环境领域的非线性模型中有较多应用[15-17]。

Sobol 法的核心思想是将模型输出的总方差分解为每个输入参数的方差和多个输入参数间相互作用的方差，然后通过输入参数对输出方差的贡献比例进行敏感性分级[18]。Sobol 法模型函数可表示为

式中，Y为模型输出值；X={X1，X2，…，Xn}，其为模型的输入参数数据集。

将函数f(X)的总方差D(Y)表示为每个输入参数的方差和多个输入参数间相互作用的方差之和，即

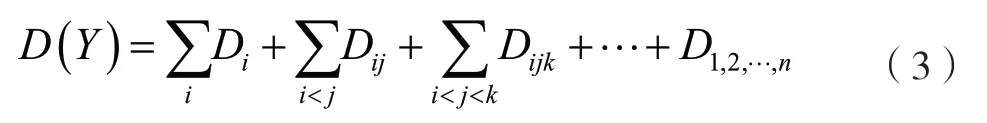
式中：Di为输入参数Xi产生的方差；Dij为输入参数Xi和Xj相互作用产生的方差；Dijk为参数Xi、Xj和Xk共同作用产生的方差；D1，2，…，n为参数模型X1、X2、…、Xn共同作用产生的方差。

根据对总方差D(Y)的贡献比例，可计算得到各阶Sobol 敏感性指数。

一阶敏感性指数用公式可以表示为

二阶敏感性指数用公式可以表示为

总敏感性指数用公式可以表示为

式中：Si用于表征输入参数Xi单独作用的敏感度；Sij为输入参数Xi和Xj相互作用的敏感指数；STi为参数Xi的总敏感性指数；D～i表示除参数Xi外其他参数共同作用产生的方差。

2 结果与分析

2.1 模型的构建及模拟结果评价

利用2016—2018年西南交通大学站O3浓度数据和温度、相对湿度、大气压力、太阳辐射强度、混合层高度、风速等气象监测资料作为学习样本数据集，应用Python3.7 软件构建BP 神经网络预测模型，训练过程的误差曲线如图1所示，在第8 285 次训练时，输出误差已收敛至0.5。选取2019年O3浓度监测数据和气象数据作为验证样本数据集，运用构建的神经网络模型，对2019年O3浓度进行预测，将预测值与观测值进行分析对比，以此评估模型的可靠性。

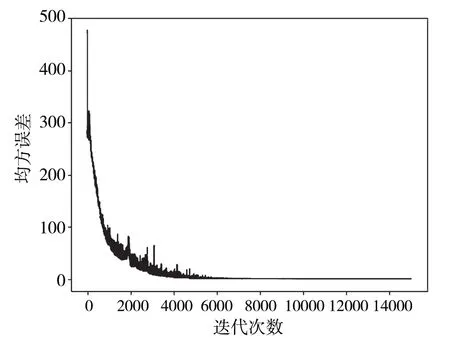
图1 BP 神经网络训练误差曲线

将2019年4月、7月、10月、1月作为春夏秋冬代表月，对比臭氧日均浓度的预测值和监测值，如图2所示。从图2可以看出，O3浓度预测值和监测值的变化趋势整体一致，两者的NMB、NME及相关系数R如表1所示。

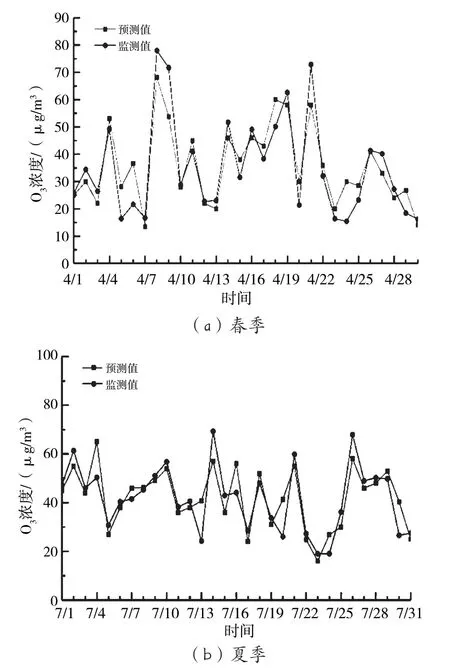
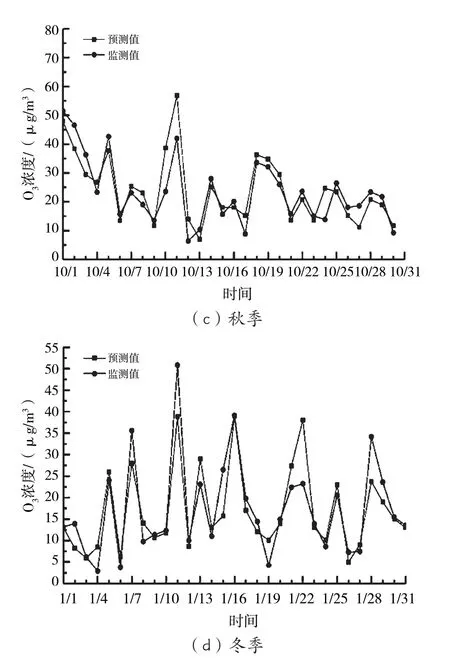
图2 2019年四季臭氧日均浓度的预测值和监测值对比

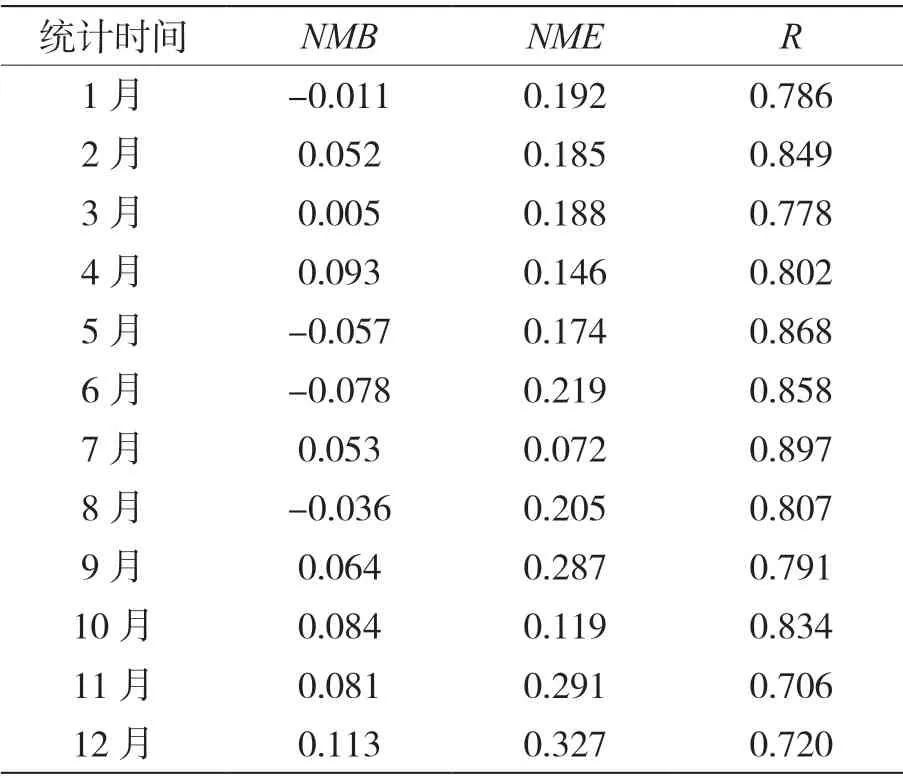
表1 BP 神经网络模型模拟结果评价指标

由表1可知，BP 神经网络模型输出值与实际监测值吻合度较高，逐月相关系数均大于0.7，其中7月模型输出值和实际监测值的相关性最高，相关系数R达0.897；NMB的绝对值均小于0.12，NME的值保持在0.072～0.327，这表明模型输出值和实际监测值的偏离程度较小。因此，可利用该模型对O3浓度进行预测，进而用于后续全局敏感性分析。

2.2 O3 浓度对各气象因子的敏感性分析

2.2.1 敏感性指数计算

由于Sobol 法的求解过程计算量较大，且存在高次积分，计算难度大，因此本研究采用基于蒙特卡洛的估计来模拟积分求解过程[19]，计算输入参数的一阶敏感性指数、二阶敏感性指数以及总敏感性指数。本研究利用2016—2019年的污染物浓度和气象监测数据分析O3浓度变化对各气象因子的敏感性，其中输入参数共计6 个，分别为温度、相对湿度、大气压力、太阳辐射强度、风速以及混合层高度，输出参数为O3浓度。下面分析具体的抽样和计算过程。

首先，将温度、相对湿度、大气压力、太阳辐射强度、风速以及混合层高度分别视作输入变量X1、X2、X3、X4、X5、X6，采用Sobol 随机序列采样方法在各输入参数变化范围内随机抽样7 000 次，生成两组样本，将抽取的样本分为矩阵A和矩阵B。

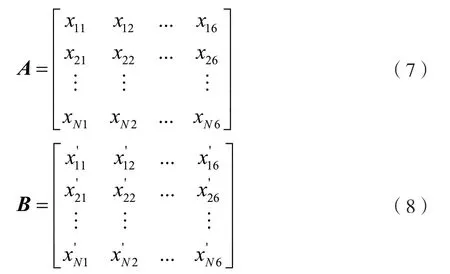
式中：N代表样本点个数，为3 500 个。

其后，用矩阵A中的某列数据替换矩阵B中的对应列，生成新的矩阵Ci；将矩阵A中的某列数据替换为矩阵B中的对应列，生成新的矩阵C～i。矩阵Ci和C～i可以表示为

其次，将矩阵生成的每组输入参数输入BP 神经网络模型进行计算，可得到对应每组输入参数的模型响应输出值，根据式（11）至式（14）计算模型响应的方差估计和各参数敏感性指标。

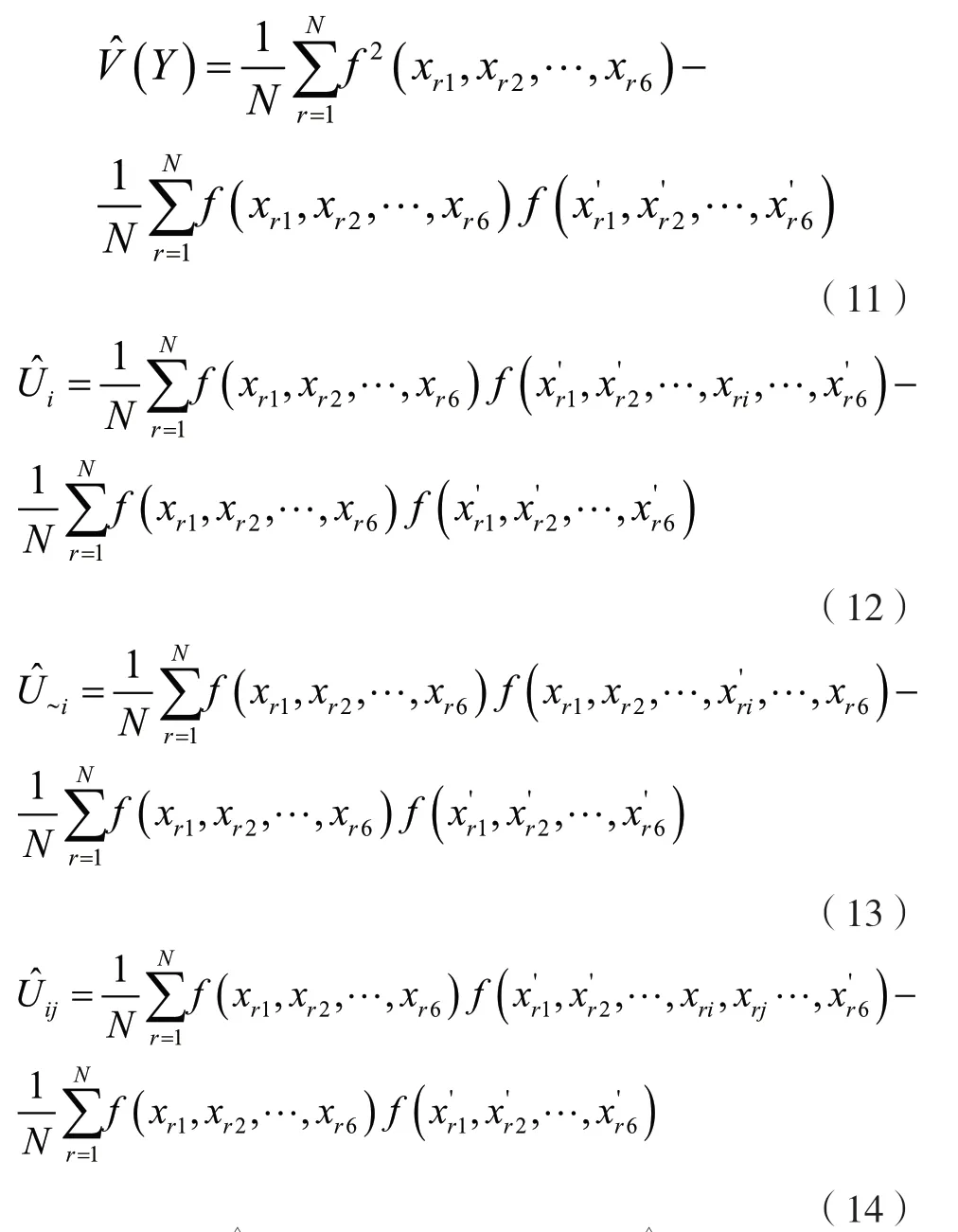
式中：表示模型总方差；表示输入参数Xi的方差；表示除输入参数Xi以外其他参数的方差；xr1表示第r行第1 列的参数，其他参数同理；表示输入参数Xi和Xj的方差。

傅里叶变换后的一阶敏感性指数为

傅里叶变换后的总敏感性指数为

采用上述计算方法得到傅里叶变换后两个输入参数相互作用的二阶敏感性指数，即

式中：Si用于表征输入参数Xj单独作用的敏感度。

最后，通过比较各气象因子的一阶敏感性指数、二阶敏感性指数以及总敏感性指数的大小，确定影响成都市O3污染的主要气象因子序列。

2.2.2 一阶敏感度和总敏感度

一阶敏感性指数Si是指输入参数Xi固定时模型输出响应量总方差的平均减小量与总方差的比值，可用于表征输入参数Xi单独作用时对输出方差不确定性的贡献，即各气象因子单独作用对臭氧变化的影响，Si越大，说明该气象因子Xi对臭氧浓度变化影响越大[20]。总敏感性指数STi表征了输入参数Xi对输出响应量的总影响程度，即STi除包括各气象因子的单独作用外，还包括各气象因子相互作用对臭氧浓度产生的影响。若STi和Si均较小，则表明该气象因子对臭氧浓度影响较小，且与其他气象因子的相互作用效应也很小；若STi较大而Si较小，则表明该气象因子对臭氧浓度影响较小，但其与其他气象因子的相互作用效应较大。因此，在确定影响成都市O3污染的主要气象因子序列时，既需要分析其一阶敏感度，还需要考量其总敏感度。

本研究利用大气温度、相对湿度、大气压力、太阳辐射强度、风速以及混合层高度等气象因子作为输入参数，并将其按顺序分别视作输入变量X1、X2、X3、X4、X5、X6。为减小极端值对后续分析的影响，本研究以2016—2019年各气象因子数据的第10 百分位值作为取值范围的下限，以各气象因子数据的第90 百分位值作为取值范围的上限，统计结果如表2所示。采用Sobol 随机序列采样方法在各输入参数变化范围内随机抽样7 000 次，得到矩阵A和矩阵B。根据上述方法，可以计算各气象因子的一阶敏感性指数和总敏感性指数，结果如图3所示。

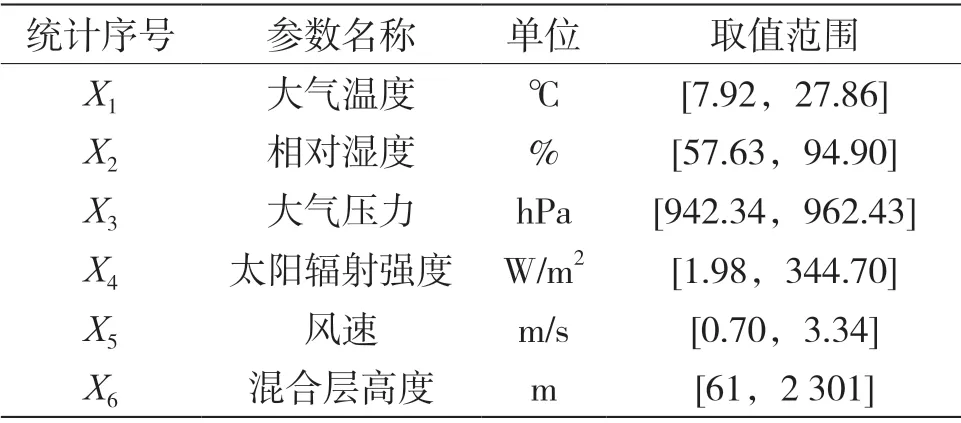
表2 各输入参数变化范围

图3直观地对比了各气象因子对臭氧的敏感度差异，柱状图分为上下两部分。图3中，下柱体代表一阶敏感度；上柱体表示除一阶敏感度以外的总敏感度部分，即参数的相互效应；下柱体加上柱体的和表示总敏感度。若某输入参数的总敏感度超过阈值0.1，则定义该参数为敏感参数[21]。可以看出，不同气象因子的一阶敏感度和总敏感度差异较大。对一阶敏感性指数进行对比，结果表明，各气象因子对成都市臭氧浓度的影响大小排序为太阳辐射强度X4（0.220 3）＞大气温度X1（0.218 7）＞混合层高度X6（0.068 2）＞相对湿度X2（0.037 3），气压X3（0.005 8）和风速X5（0.000 8）的单独作用对臭氧的影响极小。温度、相对湿度、太阳辐射强度和混合层高度的总敏感性指数均大于0.1，其中，太阳辐射强度总敏感性指数最大（0.616 9），其后依次为温度（0.560 7）、混合层高度（0.516 0）和相对湿度（0.260 0），气压（0.029 6）和风速（0.044 8）对臭氧的影响则较小。此外，每个气象因子的一阶敏感度占总敏感度的比例均较小，这表明各气象因子的相互效应是影响臭氧浓度的重要因素。

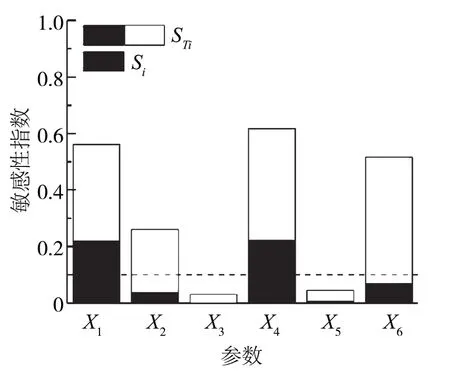
图3 各气象因子对臭氧浓度的一阶敏感度及总敏感度

2.2.3 二阶敏感度

二阶敏感性指数Sij可以反映输入参数Xi和Xj的交互效应对输出响应量的影响，其在本研究中用于表征两个气象因子相互作用对臭氧浓度的影响。Sobol敏感性分析中，将二阶敏感性指数按大小划分为不同区间，分别为很敏感、敏感和不敏感[22]，如表3所示。

表3 各气象因子对臭氧浓度的二阶敏感度

表4统计了各气象因子的二阶敏感性指数。可以看出，臭氧浓度对温度、太阳辐射强度和混合层高度的相互作用都敏感（Sij≥0.01），其对温度和太阳辐射强度的相互作用最为敏感（Sij=0.020 9）；其次为温度和混合层高度的相互作用（0.015 5）；太阳辐射强度和混合层高度的相互作用排名第三（0.012 4）；臭氧浓度对其他气象因子相互作用的敏感度极小，可视作不敏感。

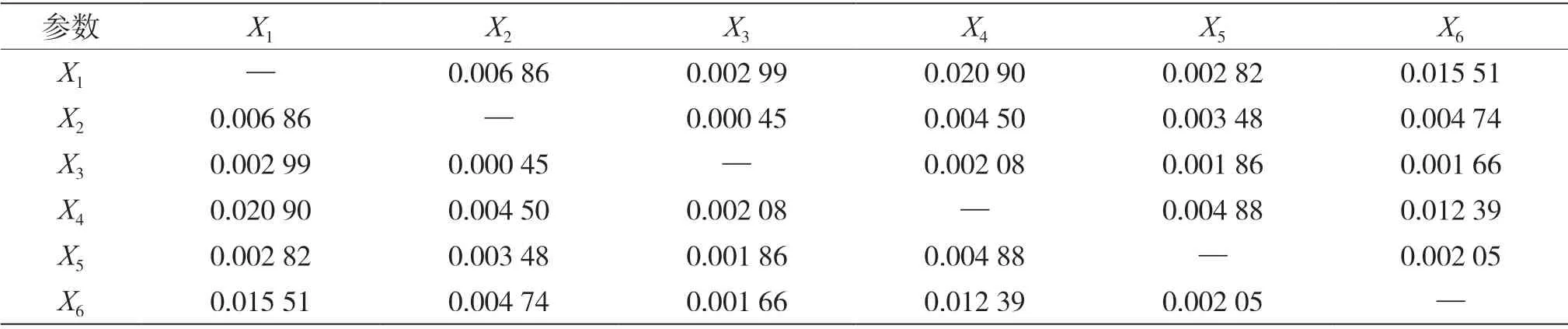
表4 各气象因子对臭氧浓度的二阶敏感度

3 结论

一阶敏感性指数分析结果表明，成都市各个气象因子对臭氧浓度的敏感性排序为太阳辐射强度（0.220 3）＞温度（0.218 7）＞混合层高度（0.068 2）＞相对湿度（0.037 3），气压（0.005 8）和风速（0.000 8）的单独作用对臭氧的影响极小。二阶敏感性指数分析结果表明，臭氧浓度对温度、太阳辐射强度和混合层高度的相互作用较为敏感，其中臭氧对温度和太阳辐射的相互作用最敏感，其次为温度和混合层高度的相互作用，太阳辐射和混合层高度的相互作用排名第三，其他气象因子的相互作用对臭氧浓度的敏感性极小。总敏感性指数分析结果表明，成都市温度、相对湿度、太阳辐射强度和混合层高度的总敏感性指数均大于0.1，气压、风速的总敏感性指数均小于0.1，其中太阳辐射强度总敏感性指数最大（0.616 9），其后依次为温度（0.560 7）、混合层高度（0.516 0）和相对湿度（0.260 0），气压（0.029 6）和风速（0.044 8）的总敏感性指数则极小，即主要影响成都市臭氧浓度变化的4 种气象因子分别为太阳辐射强度、温度、混合层高度和相对湿度。