含参量定积分的求解技巧

武燕玲 付 柯 贺春梅 麻 欢 石璐洁 李喜彬

(内蒙古师范大学物理与电子信息学院，内蒙古 呼和浩特 010022)

一、引 言

在求解定积分的过程中，通常会遇到形如

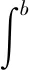
这里先介绍一个定理

设(,)与∂(,)均在矩形区域≤≤,≤≤上连续，则函数在[，]上具有连续的导数′()，且

此定理给出了求导和积分可以交换的充要条件，由于我们下面所计算的积分中被积函数的连续性以及偏导数的连续性均可以保证，故在具体求解的过程中不再证明其交换顺序的合理性

二、含参量的定积分

先看两个利用一阶导数求解的例子

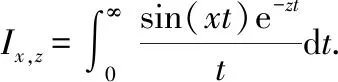
对求偏导，可得到

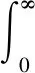
上式为关于参量和定积分，采用分部积分法，

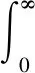
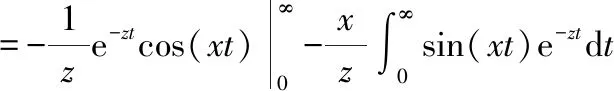
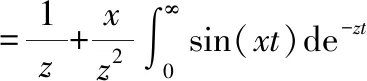
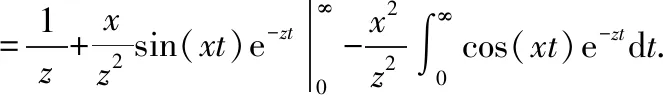
上式的最后一项积分可以利用分步积分法来进行求解

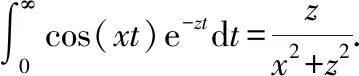
由于积分与求导具有互逆关系，对上式进行积分:

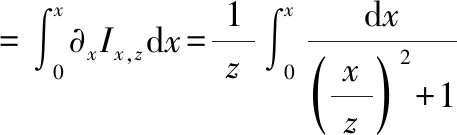
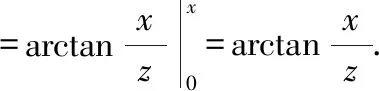
此题得解

以上的计算方法是在本题满足积分与求导互逆条件的基础上，先对参量求偏导再对其进行积分得到的读者可自行类比，尝试对求偏导再积分得到相同结果

但有些积分中并不包含参量，处理方法是在被积函数的适当位置插入参量，使之变为积分的形式，进而求解，最后根据原题对插入参量取适当的值，即可得解下面来看一个具体的例题

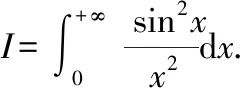
本积分中不含有如例1中的未知数，故我们在积分的三角函数部分引入参数

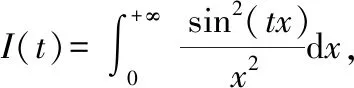
上式显然有(0)=0对求导，得到

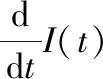
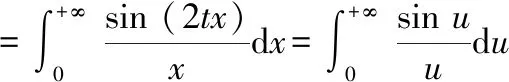
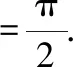
上面的积分结果可参考专著[2]此时，对上式求积分，移项后可以得到()的表达式

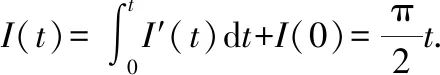
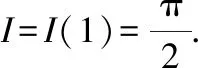
下面介绍一个和反三角函数有关的例子解题思路仍采用求导再积分的方法

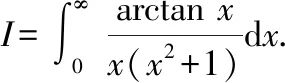
本积分中不含有如例1中的未知数，故我们在反正切函数中引入参数

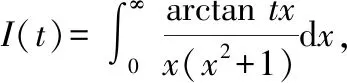
显然有(0)=0对求导得到具体值

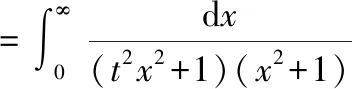
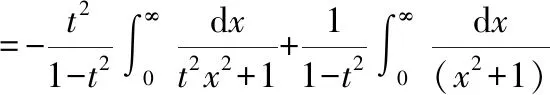
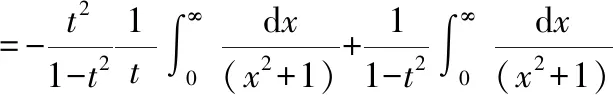
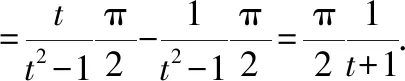
第二步用到了有理分式的拆解方法再对上式求积分可以得到()的表达式

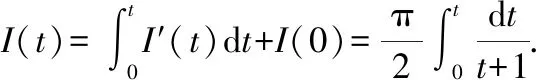
最后令=1可以得到原积分的解为

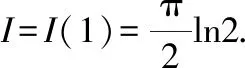
由此可见，对于我们不是很熟悉而且求积分难度相比起来较大的反三角函数，也可以利用此种方法，求解也相较而言简单了不少

在实际计算过程中，我们发现运用此种方法能解决有些定积分问题，只求一次导数无法得解，此时我们对它再次求导，得出具体的数值，最后利用二阶微分方程的性质求得通解

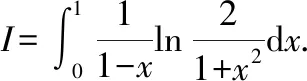
对上式进行分步积分，有

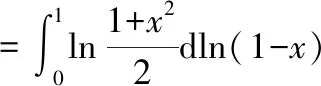
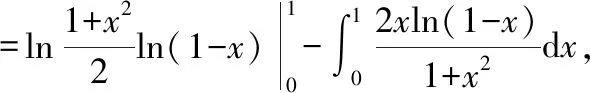
其中

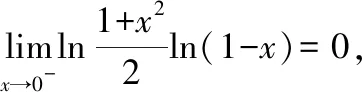
以及

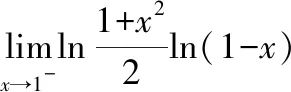
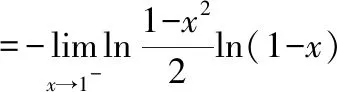
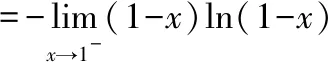
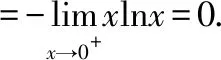
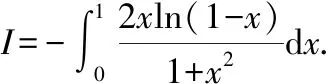
显然有(0)=0对()求导数得到

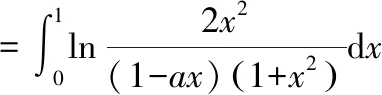
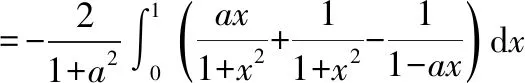
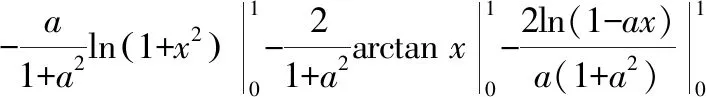
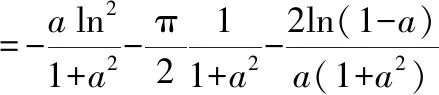
对上式进行积分，并令积分的上限为1，可得到原积分的结果为

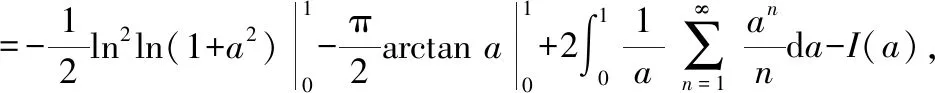
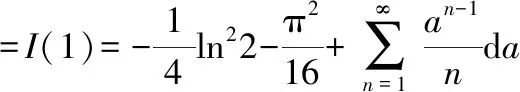
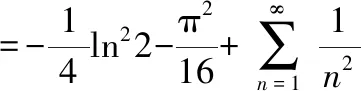
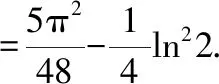
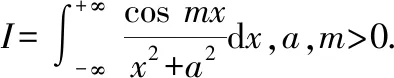
为常数，仍可引入参数

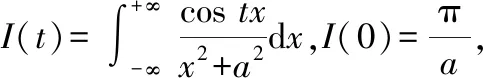
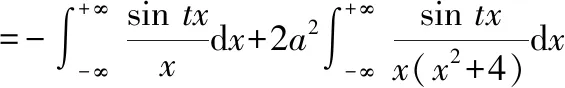
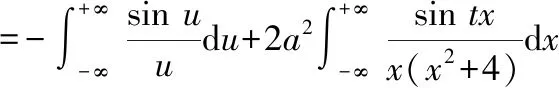
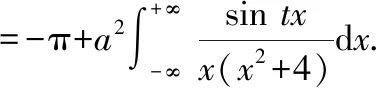
求一阶导后未得到具体数值，但可知=0时有

′(0)=-π

此时，不妨对其求二阶导数

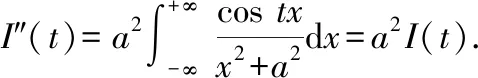
由此可得二阶齐次常微分方程

″()-()=0

通解为()=e+e-

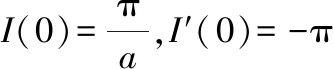
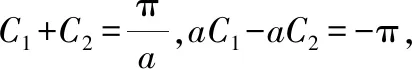
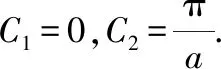
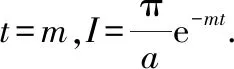
此题得解

本题虽未得到求一阶导数和二阶导数的具体值，但分别为求解提供了初始条件和二阶常系数方程，综合求得原函数即定积分的值

此题是《数学物理方法》或者《复变函数与积分变换》教材中一道经典的例题，不过该例题在上述教材均根据留数定理进行求解此例题说明，利用留数定理求解的一些积分同样可以在实变函数的范围内进行求解，只不过对技巧性要求较高

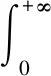
本题由于积分区间特殊，所以先利用其原函数

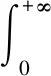
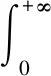
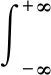
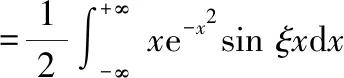
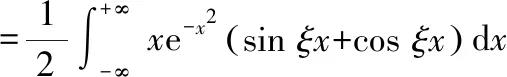
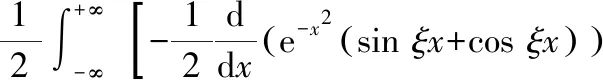
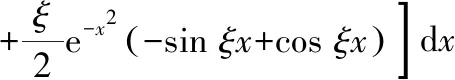
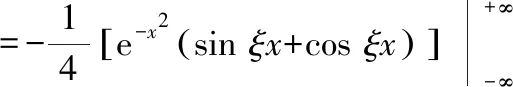
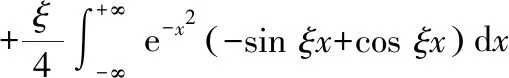
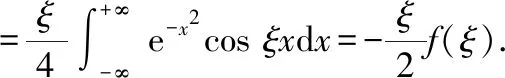
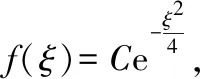
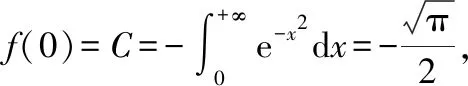
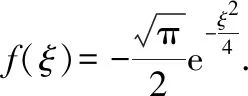
本题将待求积分看作已求导后的积分，但仍可使用上述思路求解根据函数奇偶性，将“求导后”积分区间进行变化，得到一阶微分方程，求得通解，代入初始条件，求得“原函数”最后将其求导，得到我们需要的定积分

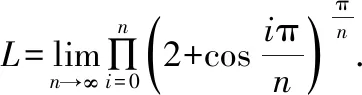
对该极限求对数，由于对数函数为连续函数，极限运算和对数函数可以交换顺序，

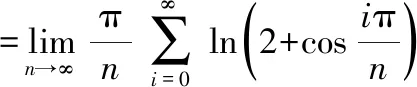
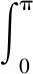
其中第三部利用了定积分的定义将上式记为一个新函数并引入参量，记

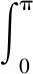
易知(0)=πln2对新函数求导，有

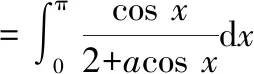
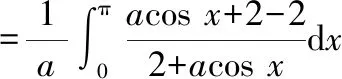
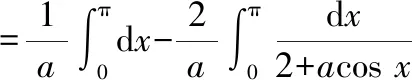
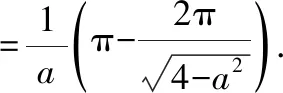
上式第四步用到了三角有理积分的“万能公式”法将所得值进行积分：

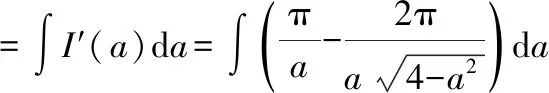
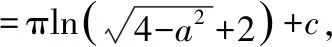
由(0)=πln2得积分常数为=-πln2，代入求得

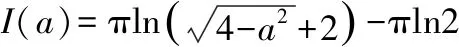
此题目为“2021年全国高等院校数学能力挑战赛”的压轴题求解此题的过程相对烦琐，需要先将乘积转换为求和的形式，利用定积分的定义，原极限变为一类特殊形式的定积分定积分的求解方法就是将其变为含参量的形式，之后求导再积分

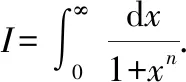
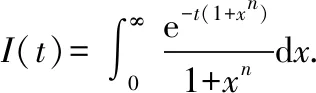
对其求导有

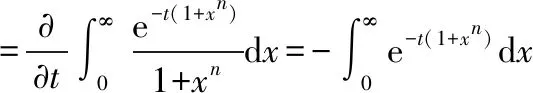
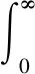
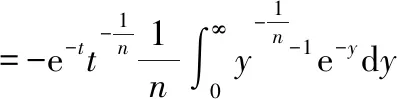
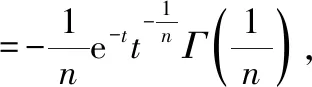
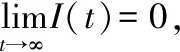
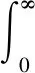
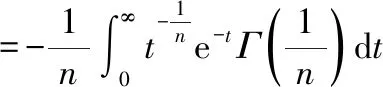
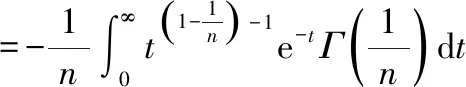
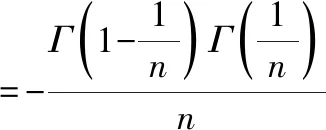
最终得到原积分的结果为

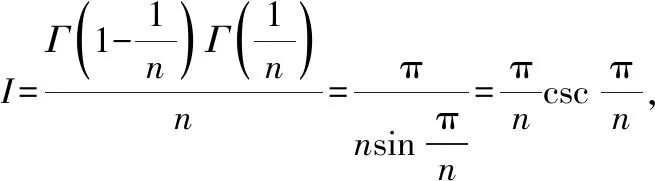
上式用到了伽马函数的性质

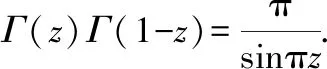
推广后，我们可引入的参量形式多种多样，如本题引入了指数形式，从而利用了伽马函数的性质，使解题变得更简单

三、总 结

含参量定积分的求解方法是众多定积分求解技巧中的一种通过以上8道例题可以看到，并无特定形式的定积分适用此种技巧，要想熟练掌握此种技巧还需大量的练习同时此种方法通常运算量较大，因此它往往出现在求解复杂定积分的过程中，但本文介绍的方法又不失为一种求解定积分的可行方法

总之，利用导数求解定积分，是一种常见的求解含参量定积分的方法，虽有一定的使用条件，但仍可求解某些定积分