基于CFD和神经网络的2级刷式密封结构泄漏和级间不平衡性分析

阎师，胡芳，黄首清，刘守文

（1.中国空间技术研究院，2.航天机电产品环境可靠性试验技术北京市重点实验室，3.北京卫星环境工程研究所：北京 100094）

0 引言

由于可以容忍刷丝束和转子瞬时不同心并保持良好的密封特性，刷式密封结构在航空发动机中获得了重要应用，是传统迷宫密封结构的重要替代产品。随着对压比、推重比要求的不断提高，航空发动机对刷式密封结构的承压能力、泄漏特性有了更高要求，而多级刷式密封技术是高压差密封的一种有效解决方案，可以同时获得更优的密封特性并减小各级的压降及刷丝束-和转子的磨损。相对于上游，下游刷式密封结构承受了大部分的压降。Hendricks等的试验表明，对于一种2级刷式密封，上游刷丝束压降为总压降的40%，而下游为60%。这种分压不均带来级间不平衡性，下游刷式束承担的较大的压差也使刷丝束和转子间的磨损较大，造成下游刷式密封性能过早失效，不利于多级刷式密封技术充分发挥其优势。因此，研究影响刷式密封结构级间不平衡的影响因素和特性具有重要意义。

目前，有关多级刷式密封技术研究主要集中于流动特性和影响因素。Qiu等利用雷诺平均N-S方程耦合非达西多孔介质模型研究了多级刷式密封与迷宫密封混合密封技术的流动特性；Pugachev等将刷丝束视为多孔介质的3维CFD模型预测一种多级刷式密封结构的泄漏特性；黄首清等基于一种3维切片模型和刷丝接触模型研究了2级刷式密封结构的泄漏、接触力和转矩特性；赵欢等研究了刷丝束径向间隙、刷丝间隙、保护间隙对级间压比的影响。需要指出的是，级间不平衡性的影响因素很多，而且具有较强的耦合性，现有研究主要为常规控制变量参数讨论，时效性和适用性不足。正交分析等方法可以较大提高参数影响分析的效率，但只能获得一些关键离散参数组合的结果。对于一些高度耦合和非线性的情况，也可采用基于2次多项式响应面方法，但是在实际应用时，响应面精度往往不足以有效逼近真实面。近年来随着人工智能技术的兴起，神经网络等方法开始应用于复杂变量模型、强耦合效应模型的结果预测，利用经过良好训练的神经网络进行数据泛化预测具有很好的时效性和适用性。

本文基于CFD模型获得泄漏量和级间压比的训练数据，设计神经网络模型进行训练，据此进行数据泛化预测，并讨论了上下游刷丝排数和保护间隙对泄漏率、级间不平衡性的影响及刷丝排数和保护间隙之间的耦合作用。

1 CFD模型

1.1 切片式几何模型

针对刷丝在周向循环对称的结构特点，建立了刷式密封结构的一种3维切片式CFD模型，即周向宽度仅包含1根刷丝，轴向包含各排刷丝。2级刷式密封结构的3维切片式CFD模型如图1所示。在模型中，上游入口和下游出口分别设置高压和标准大气压，除了入口和出口之外的边界均设置为静态墙边界。刷丝束区域的横截模型如图2所示。图中平面1～4表明了2级刷封的上下游表面所在位置，各平面的压力指面积权重平均压力。上、下游级的压差为

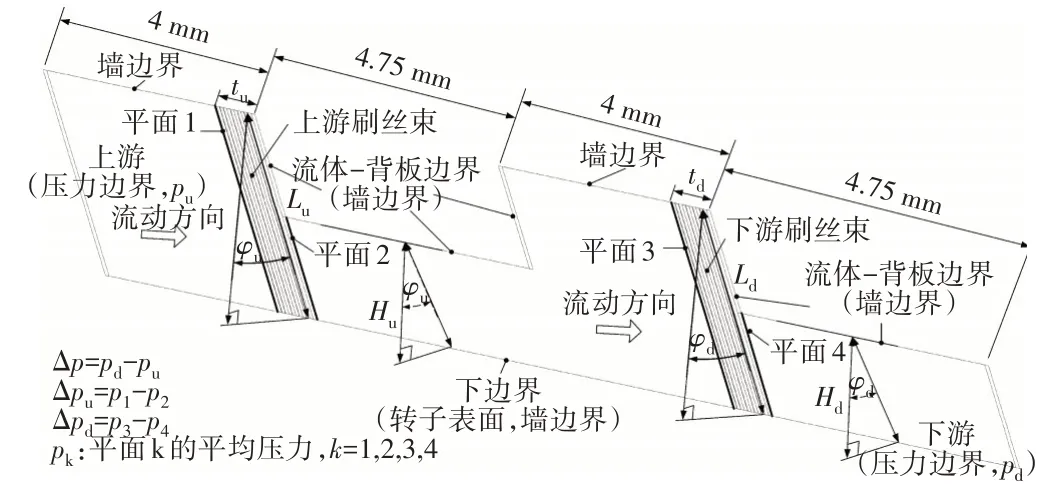
图1 2级刷式密封结构的3维切片式CFD模型

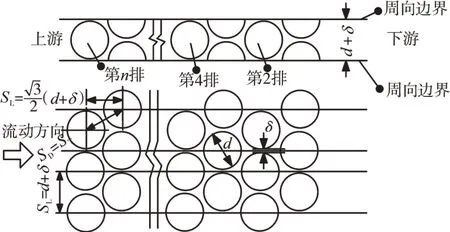
图2 刷丝束区域的横截模型

在实际的刷式密封结构中，在压差作用下刷丝束不可避免地发生压缩和变形，使研究变得极端复杂。为便于研究，并结合刷丝实际排列规律，假设刷丝为均匀间隙蜂窝状排列（图2）。Lelli等的计算表明，是否考虑压差作用下的刷丝束变形造成的流动差别小于10%，故忽略刷丝的移动和变形。

Dogu等利用多孔介质模型计算的结果表明，在刷丝根部附近压力梯度很小。故图1的模型中未对刷丝根部建模，大大减少网格数量和计算时间，且对CFD结果影响不大。

刷环的泄漏率用标况体积流率/（N·m/h）表示，与切片模型计算的质量流率/（kg/s）和周向循环数相关

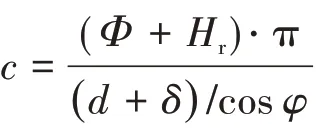
1.2 模型参数

CFD模型主要参数见表1。

表1 CFD模型主要参数

1.3 网格及CFD求解设置

计算网格如图3所示。刷丝间隙流体区域几何形状比较复杂，网格剖分非常细密，网格单元大小为0.0033 m。刷丝束的上游和下游网络剖分适中，而由于刷丝不参与流体计算且不考虑移动和变形，故刷丝网格划分最粗糙。

图3 计算网格

刷丝束内部的流动是分析的重点。对于取表1参数的2级刷式密封模型，上游来流流速不大于1 m/s，按照保护间隙1.5 mm和30℃下空气运动黏度为1.6×10m²/s，估算雷诺数为

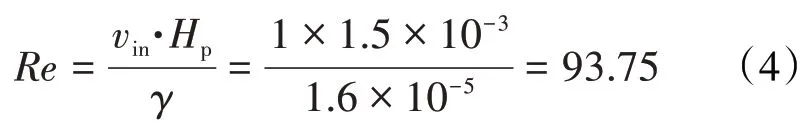
在刷丝束内部，流速一般小于100 m/s，结合刷丝直径为0.07 mm，计算对应的雷诺数为437.5。综上，2级刷式密封模型的流动被视为层流型。

计算采用ANSYS-Fluent 14.0软件，选择可压缩理想气体流动、稳态3D求解器、2阶迎风差分格式和SIMPLE算法。上述CFD模型和计算方法的准确性已通过试验证明。

2 神经网络模型

2.1 结构和算法

神经网络包括输入层、输出层和隐层。考虑到泄漏率和级间压比是反映2级刷式密封性能的重要指标，因此设置输出层神经元为2个，分别代表泄漏率和级间压比。而保护间隙和刷丝排数是影响泄漏率和级间压比的重要参数，为了区别上下游参数的影响，设置输入层神经元为4个，分别代表上游保护间隙、上游刷丝排数、下游保护间隙、下游刷丝排数。对于隐层的神经元数根据经验公式

式中：为隐层神经元数；为输入层神经元数。

因此隐层神经元数取9即可获得足够的精确性，考虑到MATLAB2019a神经网络拟合工具箱推荐的默认值是10，因此确定层数为10。这样，借助MATLAB的Neural Network Fitting工具箱建立的神经网络结构如图4所示。其中，神经元传递函数选择双曲正切的S型Tansig函数；训练函数选择Trainlm，即Levenberg-Marquardt算法；神经网络预测性能用MSE和R评价，分别是目标值与预测值的均方误差以及回归相关系数。

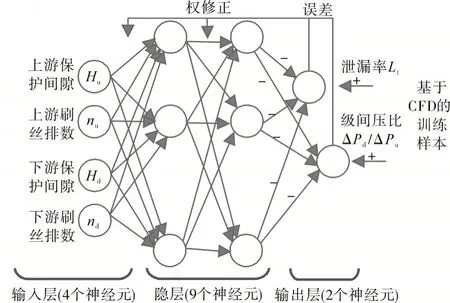
图4 用于预测泄漏率和级间压比的神经网络结构

2.2 数据训练

训练样本根据CFD模型计算，给出了不同保护间隙和刷丝排数组合下的压比和泄漏率结果，共20个样本，见表2。其中，直接用于训练神经网络的样本（训练数据）占70%，即14个；而用于验证（验证数据）和测试（测试数据）的样本分别占15%，即各3个。

训练次数与均方误差的关系如图5所示。从图中可见，训练4次后，验证数据和测试数据与预测值的均方误差基本稳定，其中验证数据与预测值的均方误差达到0.0169（均方根误差为0.13，在表2中泄漏率和级间压比2列数据的平均值18.94的1%以下）；而训练7次后，训练数据与预测值的均方误差小于10。而根据预测值与样本值的相关系数（如图6所示），二者满足很好的线性关系，相关系数达到0.99997。综上，可以认为本神经网络得到了较好地训练，可以用于泛化预测。

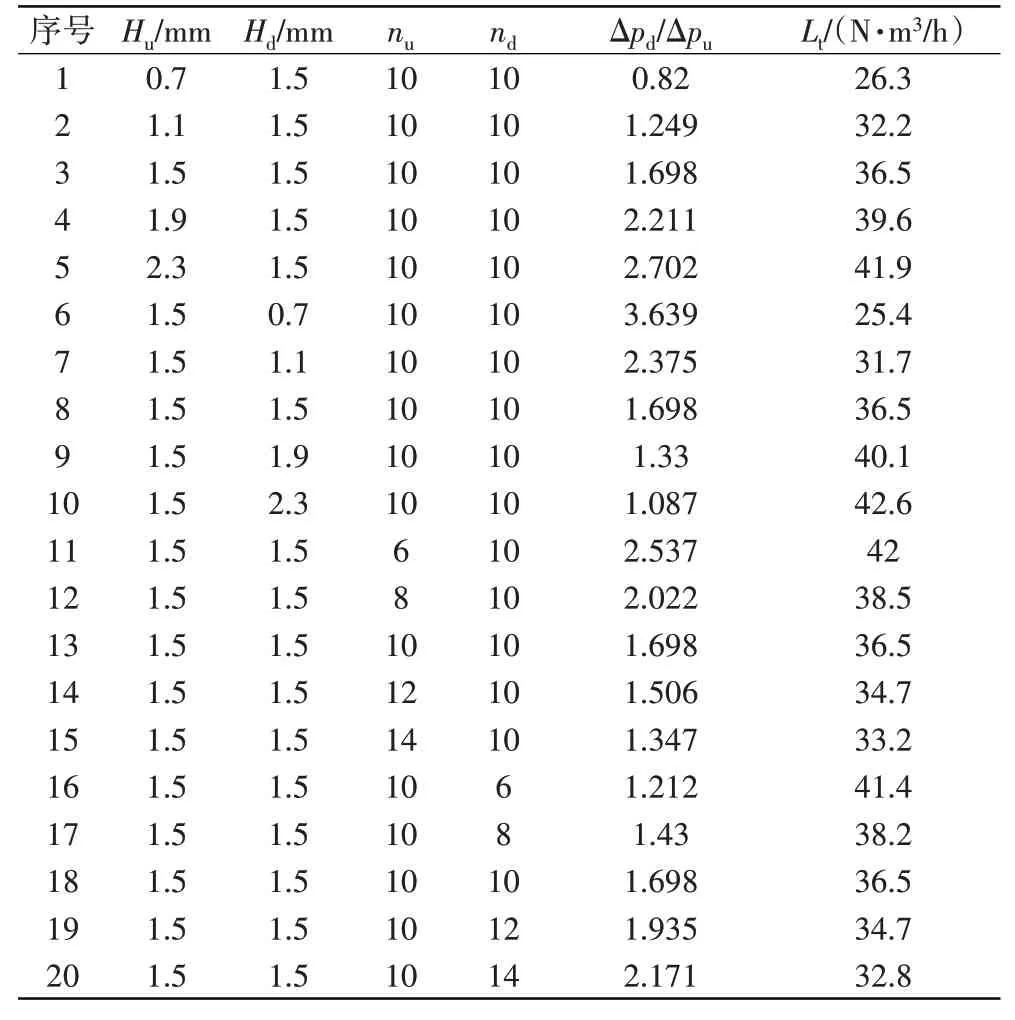
表2 训练样本

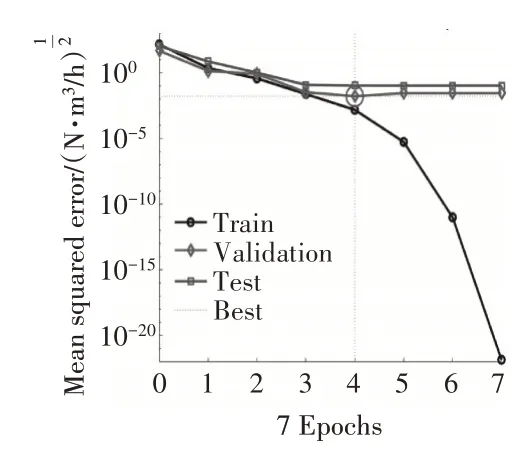
图5 训练次数与均方误差的关系

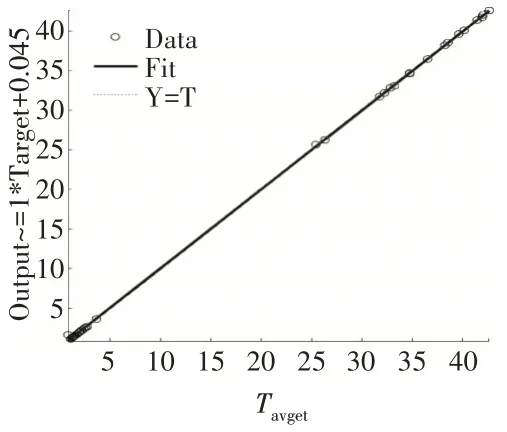
图6 预测值与样本值的相关系数

2.3 泛化预测

根据训练后的神经网络预测的50组同时改变上下游保护间隙和刷丝排数时的泛化数据分别见表3、4。表3、4分别仅改变上下游参数，其它参数按表1取值。需要指出的是，基于训练后的神经网络，这些泛化预测数据几乎是瞬间获得的，而且理论上可以得到几个参数的任何取值组合。这样，基于神经网络方法获得CFD模型的泛化数据无论在时效性还是参数组合的适用性上都有很大优势。

3 刷丝排数和保护间隙对泄漏率的耦合影响

刷丝排数和保护间隙对泄漏率的耦合影响如图7所示。从图中可见，无论是改变上游参数还是改变下游参数，泄漏率的大小和变化规律基本一致，也与直观感受一致，即泄漏率随着刷丝排数的增加而降低，随着保护间隙的减小而降低。同时，也能发现保护间隙高度和刷丝排数影响具有一定的耦合性，随着刷丝排数的增加，保护间隙对泄漏率的影响变弱；而随着保护间隙的减小，刷丝排数对泄漏率的影响也变弱。这一耦合规律可以从分析影响泄漏率主要因素的角度理解，当刷丝排数增加到一定数量后，刷丝束区域的流动阻力足够大，因此泄漏率对保护间隙的变化不敏感；而类似的，当保护间隙小到一定程度后，保护间隙区域的流动阻力足够大，因此泄漏率对刷丝排数的变化不敏感。可见，虽然这里的泄漏率数据为神经网络泛化数据，并不能从神经网络的角度对规律进行解释，但是这一泛化结果却与从物理层面的解释相吻合。

表3 同时改变上游保护间隙和刷丝排数时的泛化数据

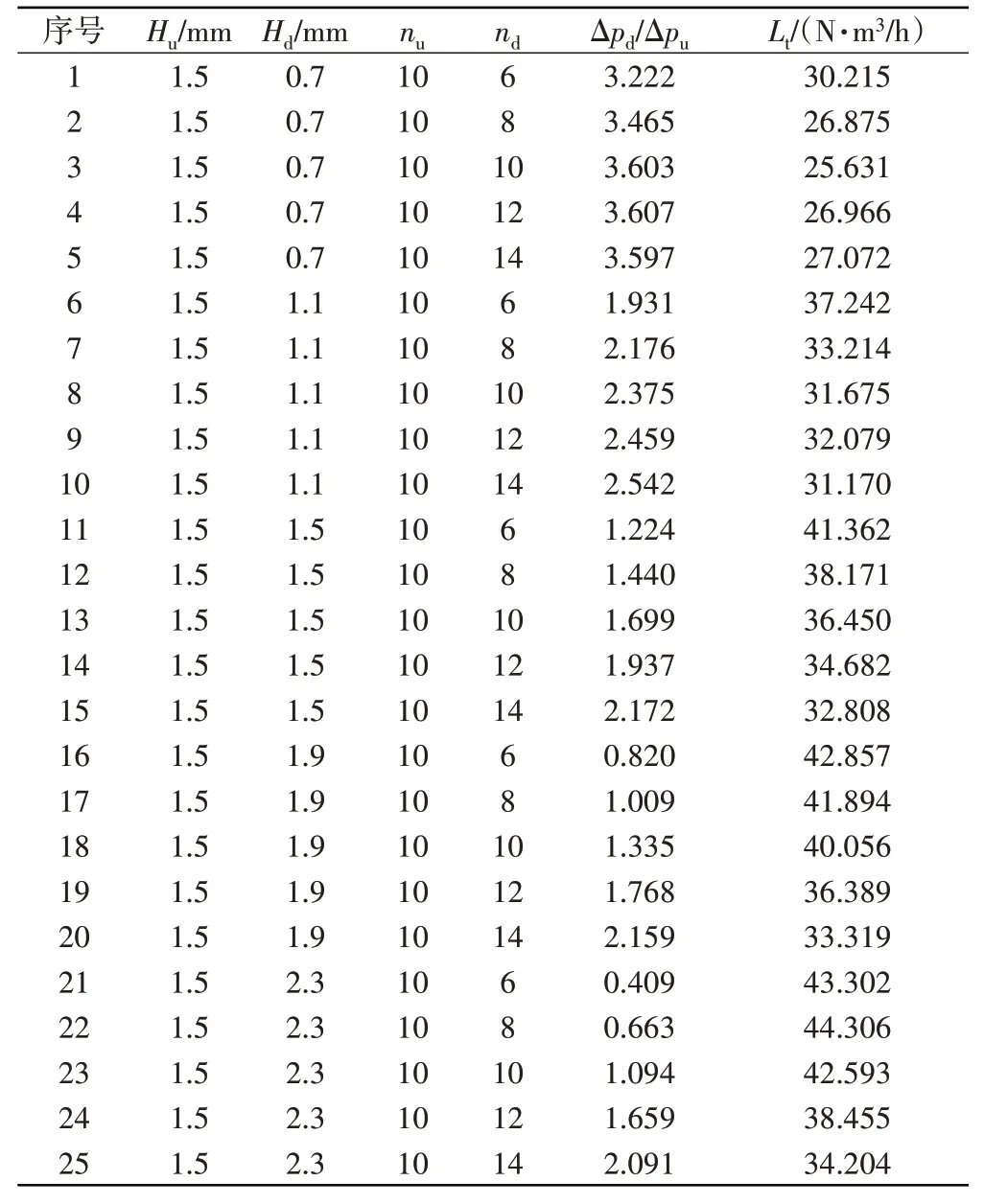
表4 同时改变下游保护间隙和刷丝排数时的泛化数据

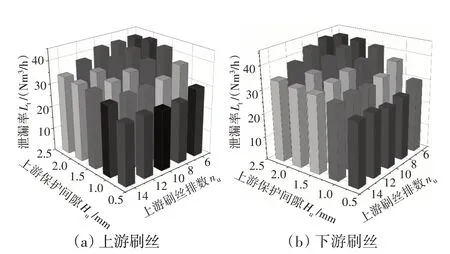
图7 刷丝排数和保护间隙对泄漏率的影响

4 刷丝排数和保护间隙对级间不平衡性的耦合影响

级间不平衡用级间压比表征，刷丝排数和保护间隙对级间不平衡的综合影响如图8所示。从图中可见，与对泄漏率的影响不同，改变上游参数与改变下游参数对级间压比的影响有较大不同。从整体看，下游参数变化对级间压比的影响更明显，最大值和最小值分别为3.61和0.41，而上游参数变化时级间压比的最大值和最小值只有3.14和1.15。仅改变下游参数时，级间压比随着刷丝排数的增大而增大，随着保护间隙的增大而减小；而仅改变上游参数时，级间压比总体上（在保护间隙为1.1～2.3 mm时成立）随着刷丝排数的增大而减小，随着保护间隙的增大而增大，与改变下游参数时趋势相反，这可以结合级间压比的定义以及参数变化对流动阻力的影响理解这一规律。

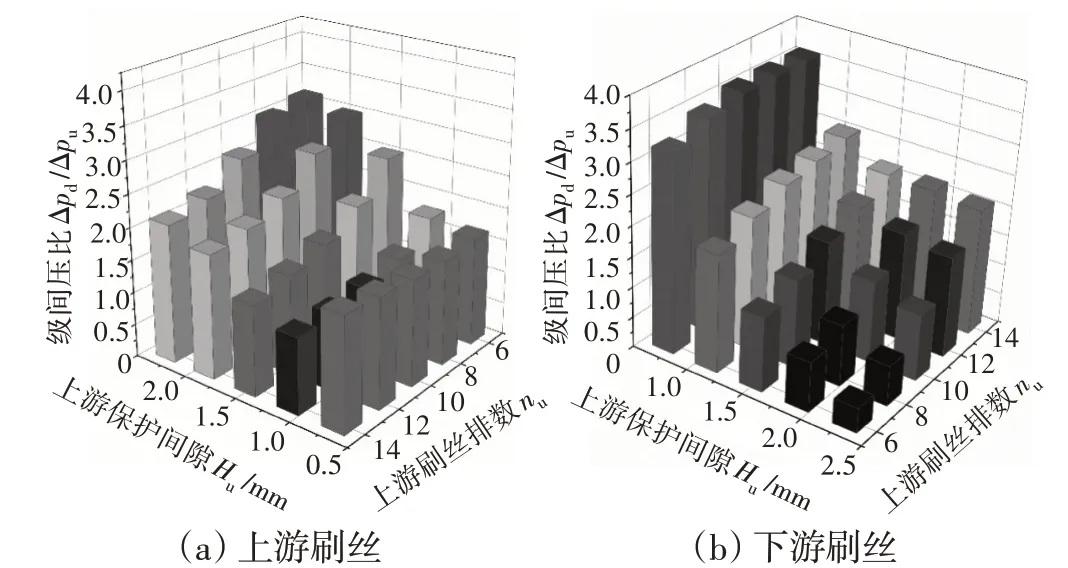
图8 刷丝排数和保护间隙对级间不平衡的影响

同样，保护间隙高度和刷丝排数影响也具有一定的耦合性。仅下游参数变化时，随着刷丝排数的增加，保护间隙对级间压比的影响变弱；而随着保护间隙的减小，刷丝排数对泄漏率的影响也变弱。而仅上游参数变化时，上述耦合性不明显。上述耦合规律类似的可以从分析影响压降主要因素的角度理解，另外由于压降主要发生在下游刷式密封结构上，也可以解释为什么下游参数影响的耦合性较强。同样，虽然这里的级间压比数据为神经网络泛化数据，并不能从神经网络的角度对规律进行解释，但是这一泛化结果却与从物理层面的解释相吻合，也可以看出神经网络适用于预测具有明显耦合性的量级刷式密封流动。

最后，还可以从泛化数据中进行参数优选。当上下游保护间隙和刷丝排数分别为1.5、1.9 mm和10、8时，级间压比为1.009，最接近1，这一取值组合可以消除级间不平衡，但对应的泄漏率较大，为41.894 N·m/h；而上下游保护间隙和刷丝排数分别为1.1、1.5 mm和14、10时，级间压比为1.155，也很接近1，而且泄漏率只有30.688 N·m/h，这一取值组合可以基本消除级间不平衡，且密封性能较好。

5 结论

（1）文中建立的神经网络训练4次后，验证数据和测试数据与预测值的均方误差达到0.0169；训练7次后，训练数据与预测值的均方误差小于10。训练样本与预测值满足很好的线性关系，相关度系数达到0.99997。

（2）根据本文算例神经网络的泛化预测数据，泄漏率随着刷丝排数的增加而降低，随着保护间隙的减小而降低；随着刷丝排数的增加，保护间隙对泄漏率的影响减小；而随着保护间隙的减小，刷丝排数对泄漏率的影响也会减小。

（3）根据本文算例神经网络的泛化预测数据，下游参数变化对级间压比的影响更明显；仅改变下游参数时，级间压比随着刷丝排数的增加而增大，随着保护间隙的增大而减小；而仅改变上游参数时，级间压比总体上（在保护间隙为1.1～2.3 mm时成立）随着刷丝排数的增加而减小，随着保护间隙的增大而增大；仅下游参数变化时，随着刷丝排数的增加，保护间隙对级间压比的影响减小；而随着保护间隙的减小，刷丝排数对泄漏率的影响也减小。而仅上游参数变化时，上述耦合性不明显。

（4）上下游刷丝排数和保护间隙对泄漏率和级间不平衡性的影响虽然源于神经网络泛化数据，却与从物理层面的解释相吻合，显示了神经网络适用于预测具有明显耦合性的2级刷式密封流动特性。

（5）针对本文算例，上下游保护间隙和刷丝排数分别为1.1、1.5 mm和14、10时，级间压比为1.155，泄漏率只有30.688 N·m/h，基本消除级间不平衡，且密封性能较好。

本研究尚有一些不足，例如神经网络技术存在过学习或欠学习现象，对训练数据的要求较高，可能对2级刷式密封流动的预测结果有影响。作者将针对以上不足开展进一步研究。