Assessing canopy nitrogen and carbon content in maize by canopy spectral reflectance and uninformative variable elimination
Zhonglin Wang ,Junxu Chen ,Jiawei Zhang ,Xianming Tan ,Muhamma Ali Raza ,Jun Ma ,Yan Zhu,Feng Yang,*,Wenyu Yang
a College of Agronomy,Sichuan Agricultural University,Chengdu 611130,Sichuan,China
b Sichuan Engineering Research Center for Crop Strip Intercropping System,Chengdu 611130,Sichuan,China
c Rice Research Institute,Sichuan Agricultural University,Chengdu 611130,Sichuan,China
d National Engineering and Technology Center for Information Agriculture,Nanjing Agricultural University,Nanjing 210095,Jiangsu,China
Keywords:Canopy nitrogen content Canopy carbon content Maize Canopy spectral reflectance Uninformative variable elimination
ABSTRACT Assessing canopy nitrogen content (CNC) and canopy carbon content (CCC) of maize by hyperspectral remote sensing data permits estimating cropland productivity,protecting farmland ecology,and investigating the nitrogen and carbon cycles in the atmosphere.This study aimed to assess maize CNC and CCC using canopy hyperspectral information and uninformative variable elimination (UVE).Vegetation indices (VIs) and wavelet functions were adopted for estimating CNC and CCC under varying water and nitrogen regimes.Linear,nonlinear,and partial least squares (PLS) regression models were fitted to VIs and wavelet functions to estimate CNC and CCC,and were evaluated for their prediction accuracy.UVE was used to eliminate uninformative variables,improve the prediction accuracy of the models,and simplify the PLS regression models (UVE-PLS).For estimating CNC and CCC,the normalized difference vegetation index (NDVI,based on red edge and NIR wavebands) yielded the highest correlation coefficients (r >0.88).PLS regression models showed the lowest root mean square error (RMSE) among all models.However,PLS regression models required nine VIs and four wavelet functions,increasing their complexity.UVE was used to retain valid spectral parameters and optimize the PLS regression models.UVE-PLS regression models improved validation accuracy and resulted in more accurate CNC and CCC than the PLS regression models.Thus,canopy spectral reflectance integrated with UVE-PLS can accurately reflect maize leaf nitrogen and carbon status.
1.Introduction
Carbon and nitrogen contents in plants are indicators of global climate change.Crop residues and roots remaining after plant death influence the balance between carbon and nitrogen levels in soil[1]and the concentrations of greenhouse gases in the atmosphere[2].Crop residues could increase soil carbon storage to slow global warming[3].Field application of crop residues with low C/N ratio can reduce soil carbon and nitrogen consumption,increasing crop productivity [1].For these reasons,monitoring carbon and nitrogen contents in crops are vital for sustainable agriculture.
Carbon and nitrogen transportation and distribution are critical processes in crop growth and development and influence grain yield and protein content [4].Researchers often use leaf nitrogen content (LNC) and leaf carbon content (LCC) to monitor crop growth status,diagnose nitrogen levels[5],and predict grain yield and quality [6,7].LNC has been widely studied but is expressed only as a nitrogen percentage in foliage,not reflecting vegetation coverage features.Canopy nitrogen content (CNC) is the product of LNC and leaf dry weight(LDW)unit ground area and reflects leaf nitrogen status and vegetation coverage [8].Developing an accurate,rapid,and nondestructive technique to monitor CNC and canopy carbon content (CCC) would advance crop growth diagnosis and productivity improvement.
With the development of smart agriculture,hyperspectral remote sensing has become a practical technique for rapid and nondestructive estimation of crop leaf carbon and nitrogen status[9].Several studies [9-11] have demonstrated that leaf nitrogen status can be accurately estimated via remote sensing.Vegetation indices (VIs) are widely used for estimating leaf nitrogen status in winter wheat and rice crops [12-14].VIs based on red and near-infrared (NIR) wavebands,such as ratio vegetation index(RVI),difference vegetation index(DVI),and normalized difference vegetation index (NDVI),show close relationships with leaf nitrogen content [15-17].Whereas a single spectral waveband is usually used for monitoring tissue nitrogen content in crops,VIs are more accurate than a single spectral waveband [14].Canopy spectral reflectance is affected by soil background and atmospheric absorption [18],but VIs can minimize interference by these noise sources and increase sensitivity to canopy vegetation features[19].Accordingly,researchers have developed VIs using complete two-by-two combinations of spectral wavebands to accurately estimate crop physiological parameters [20,21],grain yield,and protein content [22].In leaf or canopy nitrogen status estimation,red edge parameters show good performance[23,24]because they can minimize sensitivity to atmospheric absorption and scattering and soil background [25].VIs using red edge wavebands are commonly constructed to estimate crop chlorophyll content and nitrogen status [26,27].Several studies have identified close relationships between nitrogen status and VIs based on red edge wavebands.The RVI of R780/R740showed the highest correlation with the aerial nitrogen uptake of winter wheat [28].Novel double-peak area parameters with red edge characteristics were closely associated with LNC in winter wheat[29].However,current methods are inadequate for estimating the leaf carbon status of crops.Forest LCC was accurately estimated using VIs,support vector machines,and artificial neural networks[3].VIs and continuous wavelet transform(CWT)were used to assess the intercropping of soybean LNC and LCC [9].Efficient data preprocessing and modeling methods are critical for increasing the accuracy of estimation of leaf carbon and nitrogen status.
CWT is an emerging data analysis tool that uses mother wavelet functions to decompose spectral reflectance data into a series of wavelet coefficients [30].A correlation between physiological parameters and wavelet coefficients is calculated.Because wavelet coefficients can minimize the impact of canopy structures,shadows,soil backgrounds,and external environments[31],the performance of wavelet coefficients in estimating physiological parameters is better than that of VIs [32,33].Recently,CWT has been widely used for estimating leaf water content (LWC) [31],canopy chlorophyll content [34],leaf area index (LAI) [35],and dry matter mass [36] based on canopy spectral reflectance.CWT applied to water-removed spectra increased the accuracy of LNC estimation in wheat and rice [12],but carbon and nitrogen status have rarely been investigated by CWT in maize (Zea mays L.).The selection of appropriate regression models is critical to improving the estimation accuracy of carbon and nitrogen status.Linear regression models are often used for characterizing the relationship of physiological parameters to VIs or wavelet coefficients.However,partial least squares(PLS)regression models(with wavelet function as a variable) show a superior estimation accuracy with LWC than linear regression models [30].
The objectives of this study were (1) to characterize the relationships of maize CNC and CCC with VIs and wavelet coefficients,(2)to eliminate uninformative spectral parameters(VIs and wavelet functions)by uninformative variable elimination(UVE)and use the retained spectral parameters for constructing PLS regression models (UVE-PLS) of maize CNC and CCC,and (3) to evaluate the reliability of linear,nonlinear,and UVE-PLS for the estimation of CNC and CCC in maize.The anticipated results could lead to an approach for monitoring leaf carbon and nitrogen status in maize using canopy spectral reflectance,and provide datasets and spectral models allowing agronomists to estimate maize leaf carbon and nitrogen status.
2.Materials and methods
2.1.Field experimental design
Four field experiments were conducted at three locations in Sichuan,China (Fig.1A).Experimental treatments included several nitrogen fertilizer application rates and irrigation strategies with two maize cultivars during three growth stages.Table 1 shows irrigation amounts on several dates and total irrigation amounts for several irrigation regimes.A single factor randomized block design with three replications was adopted.The plant density was 6 plants m-2.Basal fertilizers of P as calcium superphosphate at 72 kg ha-1and K as potassium sulfate at 90 kg ha-1were applied at the first leaf (V1) stage.Maize growth stages were determined following Hanway [37].Weeds were eliminated by manual hoeing.The insect population was controlled with agricultural chemicals.The details of the experimental design are shown in Fig.1.
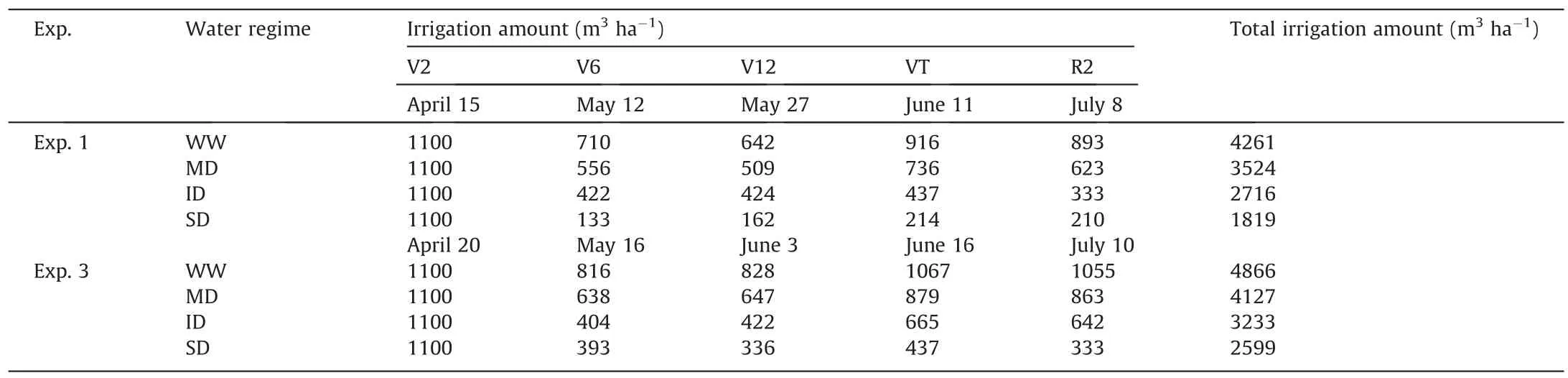
Table 1 Irrigation amount at each irrigation date and total irrigation amount under water regimes.
Experiment 1 (Exp.1): The experiment was conducted at the Modern Research Farm experimental station of Sichuan Agricultural University in Ya’an city (29°59′N,102°59′E) with a droughtresistant pool in the season of 2018.The drought-resistant pool was constructed with concrete to hold the soil and prevent the penetration of soil moisture.The plot layout of Exp.1 is shown in Fig.1B-1.Four water levels (percentage of field capacity) were applied for drought stress: well-watered (WW,60%-70%),mild drought (MD,45%-55%),intermediate drought (ID,30%-40%),and severe drought (SD,15%-25%).The semi-compact maize cultivar Zhenghong 505 was sown on April 2 and harvested on August 14.Approximately 60 kg ha-1nitrogen fertilizer (urea,46.7% N)was applied before the V1 stage,and another 60 kg ha-1nitrogen fertilizer was applied at the sixth leaf (V6) stage.Canopy spectral reflectance was measured,and plants were sampled,at the V6 and blister (R2) stages.
Experiment 2 (Exp.2): The experiment was conducted in 2018 in a field at the Sichuan Modern Crop Production Demonstration Base in Renshou county (30°04′N,104°12′E).The plot layout of Exp.2 is shown in Fig.1B-2.Three nitrogen rates were applied as urea at N1 (60 kg ha-1),N2 (120 kg ha-1),and N3 (240 kg ha-1).The cultivar Zhenghong 505 was sown on April 11 and harvested on August 20.Half of the nitrogen fertilizer was applied before the V1 stage and the other half was applied at the V6 stage.The stages of spectral measurement and plant sampling were as in Exp.1.
Experiment 3 (Exp.3): The experiment was conducted in 2019 at the Modern Research Farm of Sichuan Agricultural University in Ya’an city with a drought-resistant pool.The plot layout of Exp.3 was as in Exp.1.Four water levels were applied: WW (70%-80%),MD (55%-65%),ID (40%-50%),and SD (25%-35%).The cultivar Zhenghong 505 was sown on April 8 and harvested on August 18.Nitrogen application was as in Exp.1.Canopy spectral reflectance was measured,and plants were sampled,at the V6,tassel(VT),and R2 stages.
Experiment 4 (Exp.4): The experiment was conducted in 2019 in a field at the Sichuan Agricultural University Modern Agricultural Research and Development Base in Chongzhou city(30°33′N,103°38′E).The plot layout of Exp.4 is shown in Fig.1B-3.Four nitrogen rates were applied as urea at T1 (0 kg ha-1),T2(120 kg ha-1),T3 (210 kg ha-1),and T4 (300 kg ha-1).The semicompact maize cultivar Zhongyu 3 was sown on March 28 and harvested on August 1.Nitrogen application was as in Exp.2.The stages of spectral measurement and plant sampling were as in Exp.3.
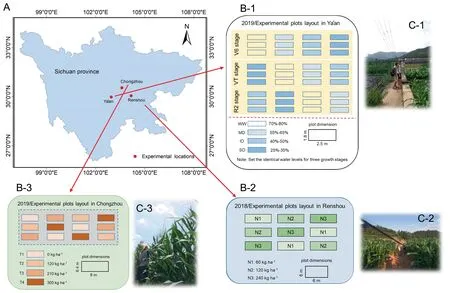
Fig.1.Locations of field experimental sites(A).Field experimental layouts in Ya’an(B-1),Renshou(B-2),and Chongzhou(B-3),Experiments 1 and 3 employed the same plot layout.In situ photos of canopy spectral reflectance measurement in Ya’an (C-1),Renshou (C-2),and Chongzhou (C-3).
2.2.Data acquisition
2.2.1.Measurement of canopy spectral reflectance
Canopy spectral reflectance measurements were performed using a field spectroradiometer with a fiber optic cable (AvaSpec-2048,Avantes,Apeldoorn,The Netherlands).A spectroradiometer was fitted with a 25°field-of-view fiber optic probe,and the spectral region was between 350 and 2500 nm.The sampling intervals were 0.6 nm from 350 nm to 1100 nm and 6 nm from 1100 nm to 2500 nm.At the V6,VT,and R2 stages (when plant heights were respectively 80-120,270-290,and 290-310 cm),canopy spectral reflectance was obtained from a height of 1 m above the canopy and 44.5 cm view diameter (view area is approximately 0.156 m-2) under a clear sky between 10:00 and 14:00 (Beijing local time).Vegetation radiation was measured at four sample sites in a plot,and each sample site received a mean of seven scans at an optimized integration time.Calibration was performed on a 25π cm2BaSO4calibration panel before and after vegetation measurement by two scans each time.
2.2.2.Measurement of CNC and CCC
After the measurement of canopy spectral reflectance,four healthy and uniform plants from each plot were destructively sampled at the V6,VT,and R2 stages and used for determining LDW(g),LNC (g 100 g-1dry weight,%),and LCC (g 100 g-1dry weight,%).The sampled plants corresponding to the positions of the acquired canopy reflectance were collected in each plot from the scanned area.All green leaves were separated from stems and oven-dried at 80°C to constant weight for each maize plant.Dried leaf samples were weighed and ground to pass through a 0.074 mm sieve.Powder samples of 50 mg were used to measure LNC and LCC by a dry combustion method.An elemental analyzer (Vario MACRO cube,Elementar,Hesse,Germany) was used for the measurement.CNC and CCC (g m-2) were calculated,respectively,as the products of LNC and LCC on a dry-weight basis and LDW per unit soil area(LDW,g m-2) [38].
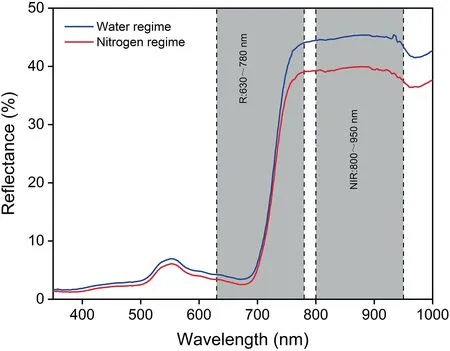
Fig.2.Mean spectra of the calibration models for water and nitrogen regimes.The wavebands of the gray shaded regions were used to calculate DVI,RVI,and NDVI.
2.3.Data analysis
2.3.1.Calculation of VIs
Canopy spectral curves of 350-1000 nm were drawn for water and nitrogen regimes (Fig.2).Because of the high signal-to-noise ratio in the waveband range of 1000-2500 nm,that range was removed.Three types of VI were used to characterize the relationship between spectrum and leaf carbon and nitrogen status(Table 2).For the calculation of RVI,DVI,and NDVI,all possible two-by-two combinations of spectral wavebands within the spectral range of 630-780 nm (red and red edge regions) and 800-950 nm (NIR region) were adopted in the form of VI coefficient matrices.The determination of wavebands for each VI was based on correlation coefficient (r) values for the relationship between every waveband combination and CNC (or CCC) in the calibration datasets.The modified normalized difference at 705 nm(mND705) and green normalized difference vegetation index(GNDVI) was calculated using specific spectral wavebands.The first derivative spectrum was used to calculate the spectral parameters for the expressions SDr/SDb,SDr/SDy,(SDr-SDb)/(SDr+SDb),and (SDr-SDy)/(SDr+SDy).Correlation analysis was performed using VIs with CNC and CCC in MATLAB 9.2(MathWorks,Inc.,Natick,MA,USA).Calibration models for CNC and CCC were established using VIs as predictors.
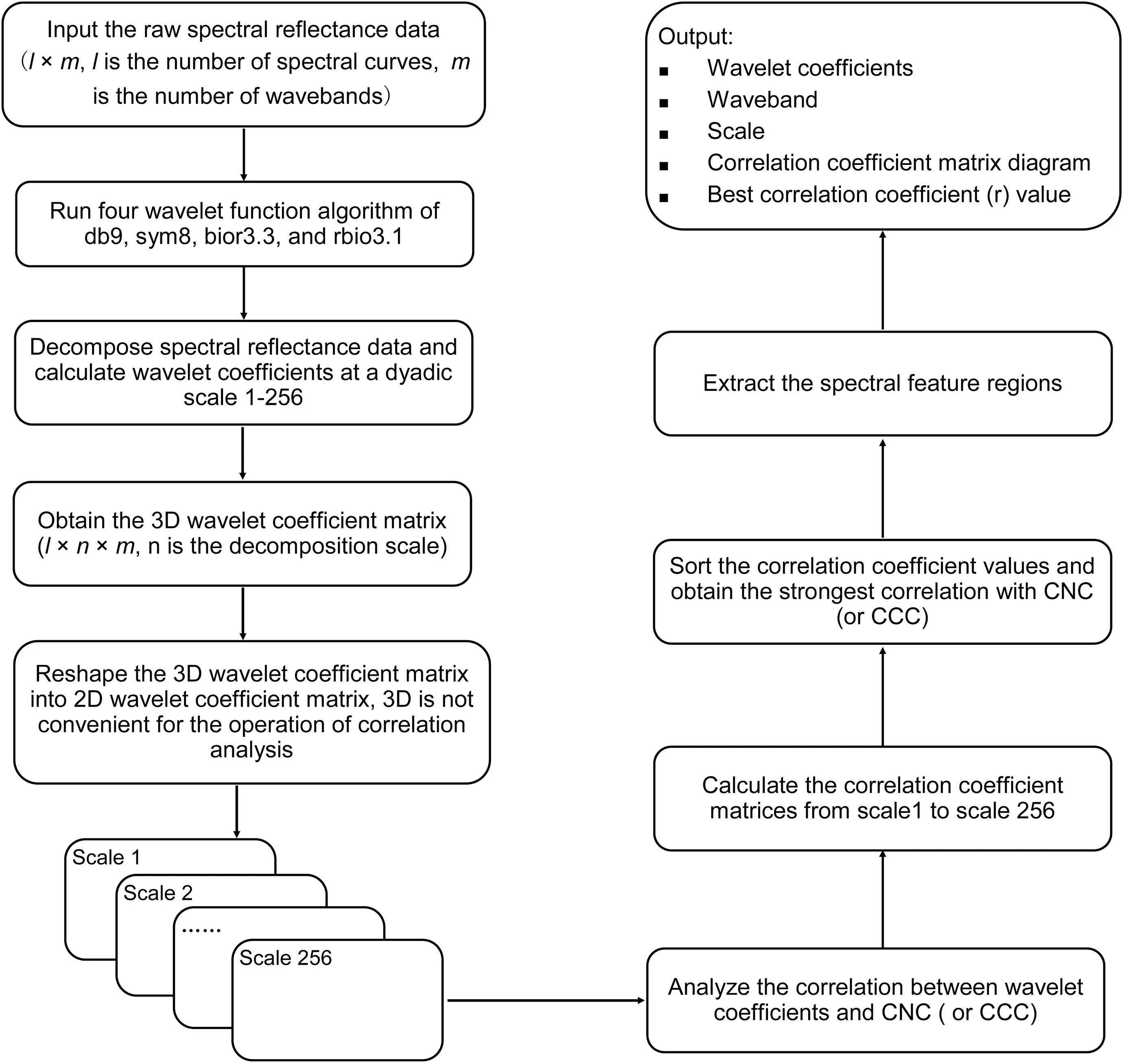
Fig.3.Workflow of correlation analysis of wavelet coefficients and CNC or CCC.
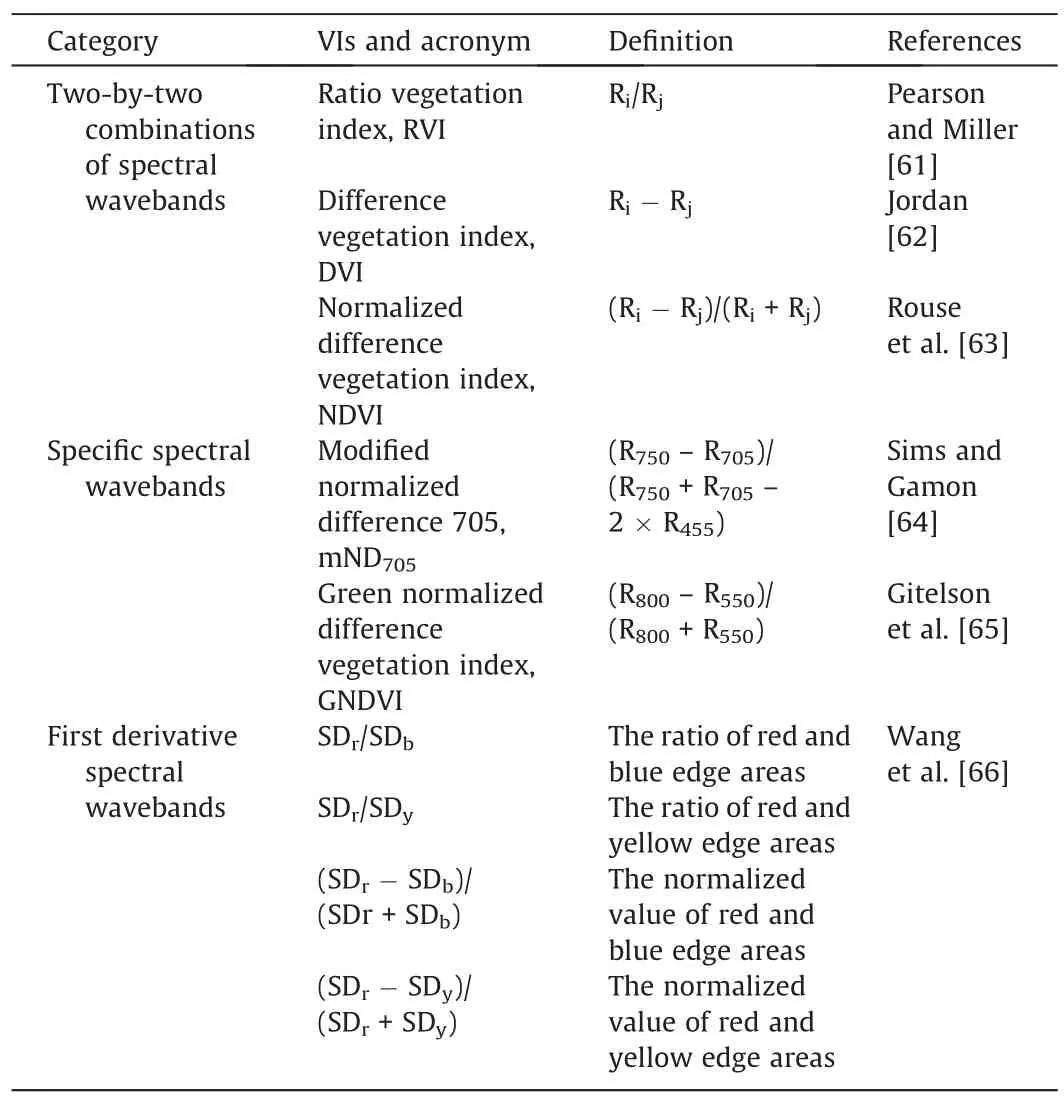
Table 2 Definition of VIs used in this study.
2.3.2.Wavelet analysis
Wavelet analysis was used for optimizing spectral reflectance data for noise reduction and decomposition[39].CWT was adopted in this study.Wavelet functions were adopted to transform spectral reflectance data into a series of wavelet coefficients at different scales[40].Wavelet coefficients were used for monitoring leaf carbon and nitrogen status.The wavelet function was calculated using the following equation [41]:

where ψa,b(λ)is the wavelet function,λ represents the spectral wavebands (λ=651),a is the scaling factor that defines wavelet scales(a is the positive integer),and b is the shift factor that determines wavelet position.The output of the wavelet function was calculated as follows:
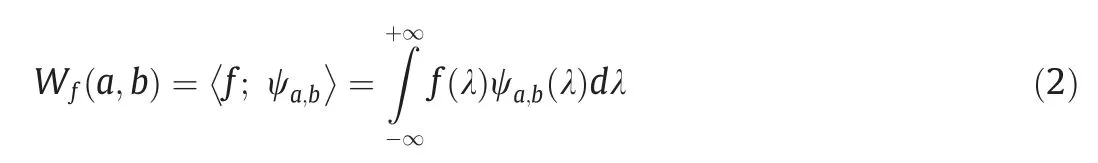
where Wf(a,b)is the wavelet coefficients and f(λ )is the raw spectral reflectance.
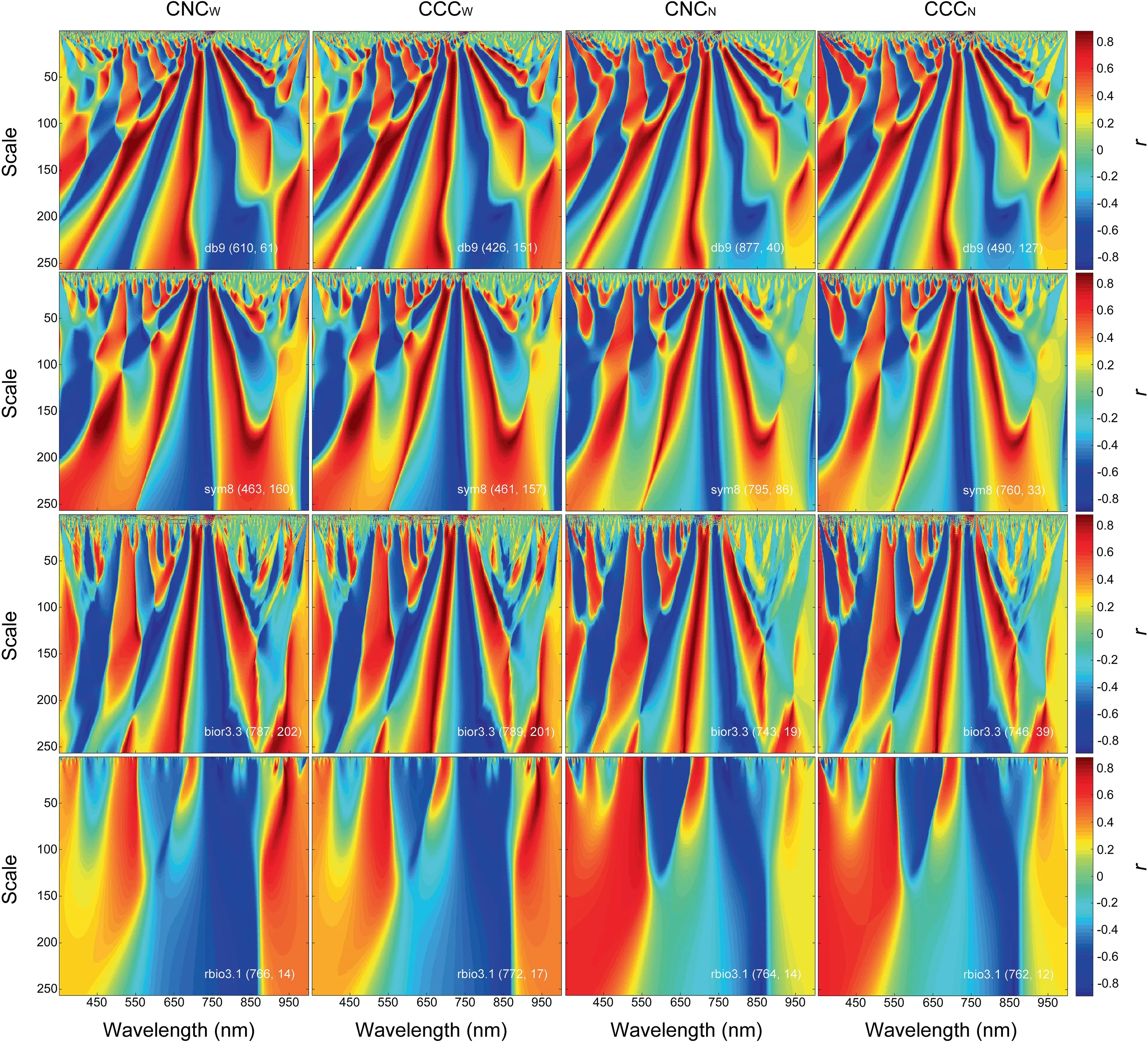
The wavelet functions of daubechies 9(db 9),symlets 8(sym 8),biorthogonal 3.3 (bior 3.3),and reverse biorthogonal 3.1 (rbio 3.1)were used for calculating wavelet coefficients at a dyadic scale of 1-256 (Fig.3).First,raw spectral reflectance data were input and transformed into wavelet coefficient matrices with a wavelet function from scale 1 to scale 256.The wavelet coefficients at a specific scale were then correlated with CNC and CCC for the production of a correlation coefficient matrix.The spectral feature region was determined based on the correlation coefficient matrix.The correlation between the wavelet coefficient matrix and CNC (or CCC)was calculated to identify the waveband and scale with the strongest correlation with CNC (or CCC).Outputs were the correlation coefficient matrix diagram,best correlation coefficient (r),corresponding wavelet coefficients,waveband,and scale.Wavelet coefficients were used to establish calibration models of CNC and CCC.The CWT was performed using our self-developed program in MATLAB.
2.3.3.UVE-PLS
UVE is a variable selection method based on the stability analysis of the PLS regression model and is used to eliminate redundant or uninformative spectral parameters [42].The validity of spectral parameters included in the PLS regression model was investigated using UVE.For each spectral parameter,stability was assessed for the computation of the reliability measure hiwith the PLS regression coefficient.The UVE-PLS approach can be generalized as follows:
1) The spectral parameter matrixX(real variable matrix) was input to the MATLAB software.Then the UVE-PLS program was run to compute the random variable matrixRusing VI coefficients and wavelet coefficients,having the identical size of the real variable matrixX.
2) The matricesXandRwere combined to form an extended matrixXR.The PLS regression model was fitted using the matricesXRandY(CNC or CCC).
3) Cross-validation was used to exclude samples,obtaining one regression coefficient vector b by eliminating one sample to produce the regression coefficient matrixB.The regression coefficient contributed to establishing the PLS regression model of the corresponding variable.Thus,the following equation can be used in the quantitative measurement of the stability of all variables.

where meiand stdiare respectively the mean and standard deviation of the PLS regression coefficient of variable i.
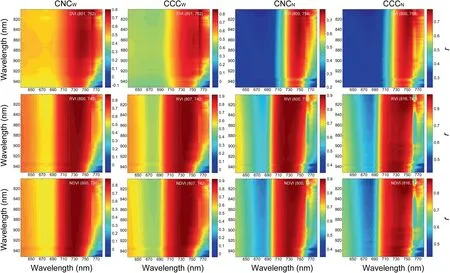
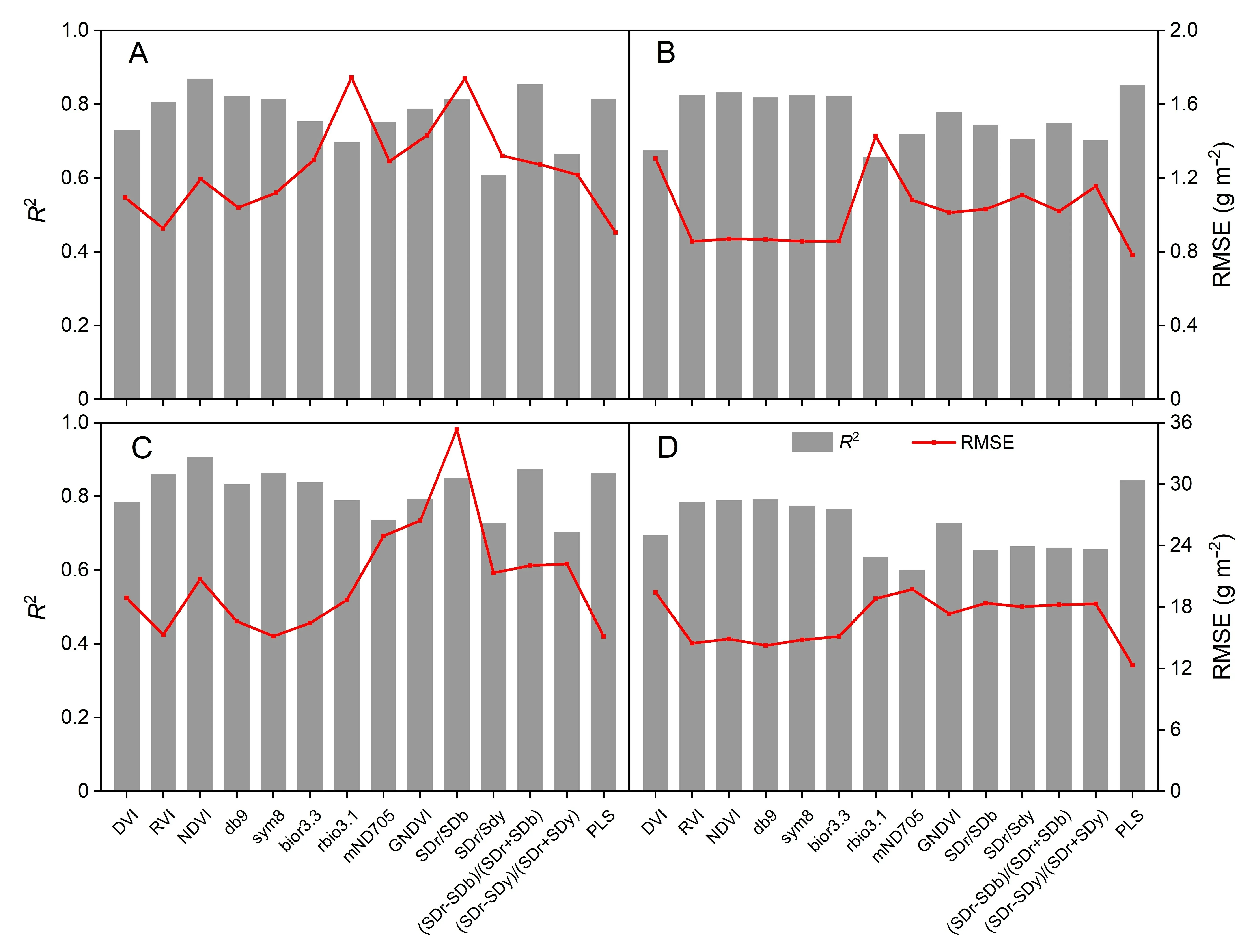
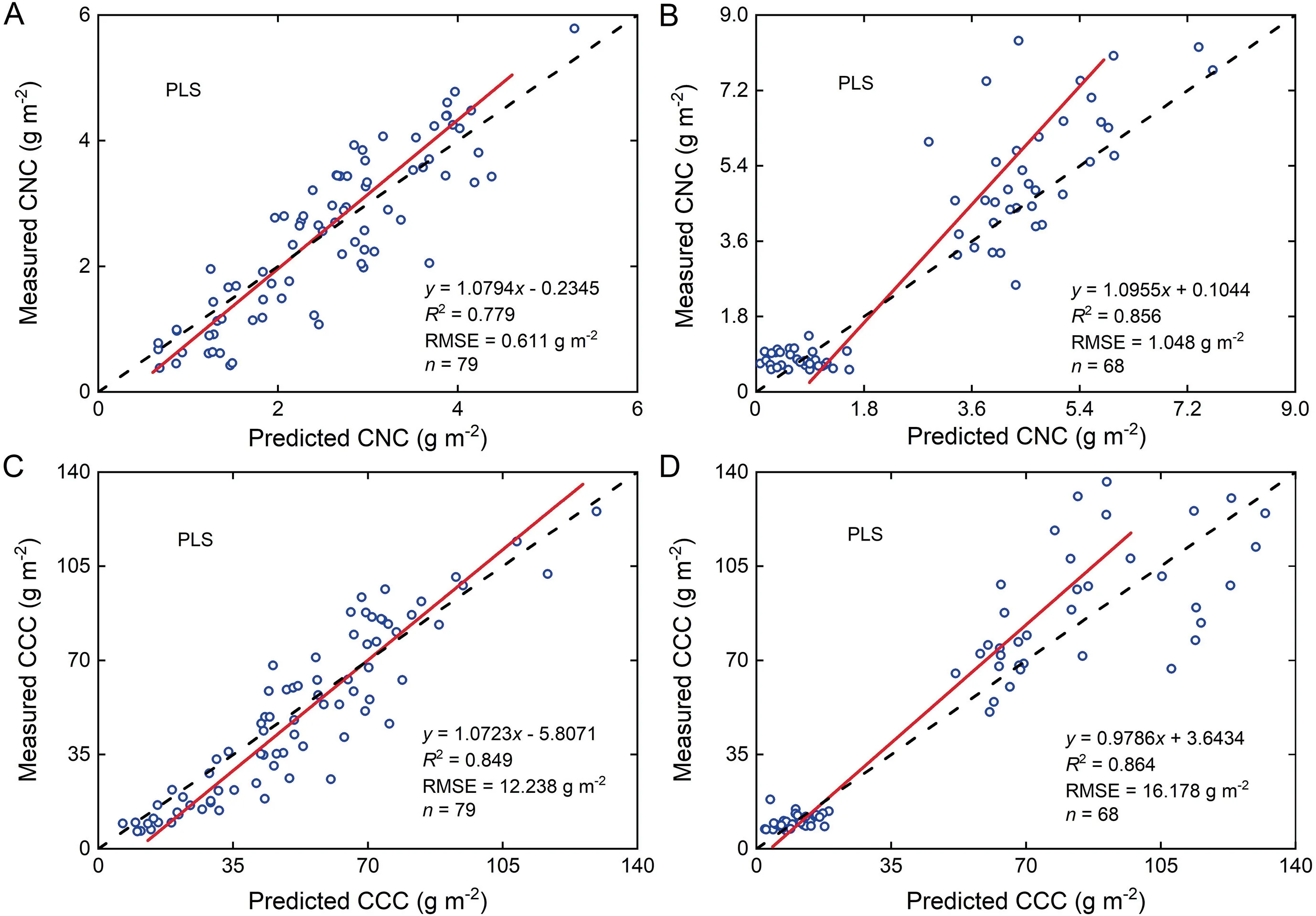
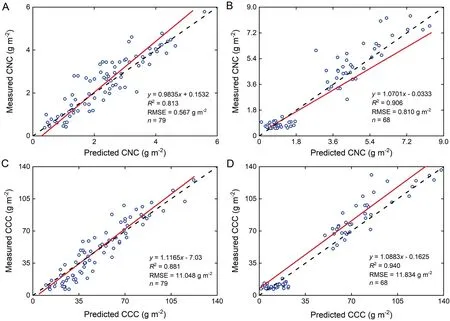
4) The threshold value hmaxwas determined using the maximum absolute value hiin the random variable matrix.When|hi| 5) The high absolute value of the reliability measure hiprovided valuable information for the PLS regression model.UVE-PLS was run until a new random variable matrix could not be calculated.The results of the UVE-PLS operations were compared,and the PLS regression model with the highest accuracy was retained. All data of each experiment were merged to establish and validate the estimation models of CNC and CCC.The datasets for water and nitrogen regimes were analyzed separately.The data from 2019 were used in constructing the calibration models of CNC and CCC.The calibration models were validated using the data from 2018.Statistical results obtained with calibration and validation datasets are shown in Table 3.VIs and wavelet coefficients were adopted for CNC and CCC estimation using linear and nonlinear (quadratic,exponential,power,and logarithm) regression models.All spectral parameters (VIs and wavelet functions) were used for constructing PLS and UVE-PLS regression models.The pre-diction performance of the models was evaluated using the coefficient of determination (R2),and root mean square error (RMSE),calculated as follows: Table 3 Statistical results of maize CNC and CCC under water and nitrogen regimes. where yiand yi′are respectively the measured and predicted values for sample i,is the mean,and n is the number of samples used for calibration or validation. VI coefficients were calculated to characterize the relationship of VIs with CNC and CCC(Table 4).Using two-by-two combinations of spectral wavebands,DVI,RVI,and NDVI were strongly correlated with CNC and CCC under the water and nitrogen regimes (Fig.4).The strongest correlations,of approximately 0.9,with CNC and CCC were obtained with NDVI.The correlations between RVI and CNC or CCC were slightly lower than those of NDVI.GNDVI showed a higher correlation (r >0.8) with CNC and CCC than mND705.Difference and normalized values calculated using red and blue edge areas based on the first derivative spectrum yielded higher correlations with CCC and CNC than those of the red and yellow edge areas.Among all VIs under the water regimes,the strongest correlations with CNC (r=0.883) and CCC (r=0.923) were found at NDVI(800,736)and NDVI(807,742).Under the nitrogen regimes,the strongest correlations with CNC(r=0.908)and CCC(r=0.886)were found at NDVI (800,740) and NDVI (816,745). The correlations between wavelet coefficients and CNC(or CCC)under water and nitrogen regimes were calculated(Table 5).A correlation matrix diagram (Fig.5) illustrates the correlations between wavelet coefficients and CNC or CCC.No marked differences in correlation were found between wavelet coefficients and CNC or CCC,although the rbio 3.1 of the wavelet function showed a weaker relationship than the other wavelet functions.Under the water regimes,the sym 8 of the wavelet function showed the strongest correlation with CNC and CCC,and the correlation coefficients were 0.905 (463 nm,scale 160) and 0.921 (461 nm,scale 157),respectively.Under the nitrogen regimes,the strongest correlation of CNC was generated at bior 3.3 (r=-0.904,743 nm,scale 19),and the strongest correlation of CCC was generated at db 9(r=-0.876,490 nm,scale 127).The feature wavebands were obtained and distributed in the red edge region,and some were distributed in the blue wavebands. Linear and nonlinear models of CNC and CCC were constructed with VIs or wavelet coefficients.PLS regression models were determined by combining all the spectral parameters with the calibration dataset from 2019.Table S1 shows that VIs and wavelet coefficients had significant linear and nonlinear relationships with CNC and CCC,among which linear and logarithm functions showed lower accuracy than other functions.However,the prediction accuracy of PLS regression models after the combination of all the spectral parameters was slightly superior to those of the linear and nonlinear models.The best models were selected to estimate CNC and CCC from Table S1,as shown in Fig.6.Under water regimes,the power function of CNC showed the highest R2(0.876) and lower RMSE (1.194 g m-2) when the NDVI (800,736)was used.The NDVI (807,742) was used for estimating the CCC with the highest R2(0.906) and lowest RMSE (20.717 g m-2) for the exponential function.The PLS regression models of CNC and CCC did not result in the highest R2value,but the lowest RMSE values were calculated as 0.905 g m-2and 15.122 g m-2,respectively.Under nitrogen regimes,CNC and CCC were accurately estimated using the PLS regression model,with R2values of 0.853 (CNC)and 0.844 (CCC) and RMSE values of 0.783 g m-2(CNC) and 12.324 g m-2(CCC),respectively.Accordingly,the PLS regression model was adopted as an effective method for estimating the CNC and CCC of maize. The estimation models of CNC and CCC described above were validated with the validation dataset from 2018.Table S2 shows that the validation accuracy of the estimation models differed.The best validation results were shown in Fig.7,with 1:1 scatterplots of predicted against measured values.Under water regimes,the PLS regression models of CNC and CCC showed the best performance,with R2values of 0.779 (CNC) and 0.849 (CCC) and RMSE values of 0.611 g m-2(CNC)and 12.238 g m-2(CCC).Under nitrogen regimes,the best performance was also observed in the PLS regression models for CNC (R2=0.856,RMSE=1.048 g m-2) and CCC (R2=0.864,RMSE=16.178 g m-2).Whether in a water ornitrogen environment,the PLS regression model markedly improved the validation accuracy of CNC and CCC estimation. Table 4 Correlations between VIs and CNC or CCC under water and nitrogen regimes. Table 5 Correlations between wavelet coefficients and CNC or CCC under water and nitrogen regimes. Fig.4.The correlation coefficient(r)matrix diagram between VIs and CNC or CCC.Correlation coefficient values are represented by the colors and depths of pixels.A deeper color represents a higher correlation.CNCW and CCCW indicate respectively CNC and CCC under water regimes.CNCN and CCCN indicate respectively CNC and CCC under nitrogen regimes. Fig.5.The correlation coefficient (r) matrix diagram for wavelet coefficients with CNC or CCC.Correlation coefficient values are represented by the colors and depths of pixels.A deeper color represents a higher correlation.CNCW and CCCW indicate respectively CNC and CCC under water regimes.CNCN and CCCN indicate respectively CNC and CCC under nitrogen regimes. The threshold hmaxwas used in selecting informative spectral parameters for establishing a UVE-PLS regression model,as shown in Table S3.Informative spectral parameters and the prediction accuracy of UVE-PLS regression models varied.Compared with linear,nonlinear,and PLS regression models,the UVE-PLS regression models showed higher prediction accuracy,with lower RMSE values.Fig.8 shows the stability and prediction accuracy of the CNC and CCC estimation models.The dotted lines indicate thresholds.The reliability measure of the real variable was used for comparison with the threshold.Spectral parameters were considered uninformative and eliminated when|hi| The validation results of the UVE-PLS regression models for CNC and CCC were visualized by 1:1 scatterplots of predicted and measured values (Fig.9).Under water regimes,the best UVE-PLS regression models for CNC and CCC were achieved,with R2values of 0.813 (CNC) and 0.881 (CCC) and RMSE values of 0.567 g m-2(CNC) and 11.048 g m-2(CCC).Under nitrogen regimes,the best UVE-PLS regression models for CNC and CCC were achieved,with R2values of 0.906 (CNC) and 0.940 (CCC),and RMSE values of 0.810 g m-2(CNC)and 11.834 g m-2(CCC).The validation accuracy of the UVE-PLS regression models for CNC and CCC was higher than that of the PLS regression models. Fig.6.Prediction accuracy of calibration models for CNC and CCC under water and nitrogen regimes.(A)and(C)indicate respectively CNC and CCC under water regimes.(B)and (D) indicate respectively CNC and CCC under nitrogen regimes.DVI,difference vegetation index;RVI,ratio vegetation index;NDVI,normalized difference vegetation index;mND705,modified normalized difference 705;GNDVI,green normalized difference vegetation index;SDr/SDb,the ratio of red and blue edge areas;SDr/SDy,the ratio of red and yellow edge areas;(SDr -SDb)/(SDr+SDb),the normalized value of red and blue edge areas;(SDr -SDy)/(SDr+SDy),the normalized value of red and yellow edge areas;PLS,partial least squares;R2,coefficient of determination;RMSE,root mean square error. Fig.7.Predicted and measured plots of calibration models with the validation dataset for CNC and CCC.(A)and(C)indicate respectively CNC and CCC under water regimes.(B) and (D) indicate respectively CNC and CCC under nitrogen regimes.R2,coefficient of determination;RMSE,root mean square error;PLS,partial least squares. Fig.8.Stability(hi)and prediction accuracy of UVE-PLS regression models for CNC and CCC under water and nitrogen regimes.(A)and(C)indicate respectively CNC and CCC under water regimes.(B)and(D)indicate respectively CNC and CCC under nitrogen regimes.1-13(14-26)of x-axis is DVI,RVI,NDVI,db 9,sym 8,bior 3.3,rbio 3.1,mND705,GNDVI,SDr/SDb,SDr/SDb,(SDr -SDb)/(SDr+SDb),(SDr-SDy)/(SDr +SDy)in the real variable(random variable),respectively.R2,coefficient of determination;RMSE,root mean square error. Fig.9.Predicted and measured plots of UVE-PLS regression models with the validation dataset for CNC and CCC.(A)and(C)indicate respectively CNC and CCC under water regimes.(B) and (D) indicate respectively CNC and CCC under nitrogen regimes.R2,coefficient of determination;RMSE,root mean square error. The canopy spectral reflectance of maize is affected by canopy structure and ambient environment,and VIs can eliminate noise to some extent [44].The VIs of the two-by-two combinations of spectral wavebands,especially RVI and NDVI,showed high correlations with CNC and CCC (Table 4).This finding is consistent with those of a previous study [45].The sensitive wavebands in DVI,RVI,and NDVI for estimating CNC and CCC were distributed mainly in the red edge region.In previous studies [25,46],the red edge wavebands were more sensitive to chlorophyll.No marked differences in correlation were found for CNC or CCC with RVI and NDVI because the sensitive wavebands used were similar.However,the wavebands selected by DVI were different from those selected by RVI and NDVI,and the correlation was also weaker.We accordingly speculated that DVI might be more readily affected by stress conditions.The sensitive wavebands of CCC were obtained in the range of 730 nm and 750 nm and were found to be possibly related to the biomass of maize leaves,given that the red edge and NIR regions were more sensitive to biomass [47].Decreasing nitrogen content in a maize plant can lead to a poor foliar photosynthetic system and lower chlorophyll content,reduced photosynthetic and photoassimilation rates,and lower LCC [3].This decrease in nitrogen content may explain the finding that the sensitive wavebands of CCC were in the red edge region. The rbio 3.1 of the wavelet functions showed a weak relationship,whereas the db 9,sym 8,and bior 3.3 showed excellent performance in signal reconstruction and dimensionality reduction.Although multiple wavelet functions and decomposition scales were used in optimizing wavelet coefficients,no significant difference was observed among the correlations of the wavelet functions(db 9,sym 8,and bior 3.3) with CNC and CCC.We speculate that the relationship of the wavelet functions with CNC and CCC achieved a stable and optimum status.The spectral wavebands of CNC and CCC calculated by the CWT method were distributed mainly in the red edge region.Under water and nitrogen regimes,the blue wavebands were obtained with the db 9 and sym 8 of wavelet functions and showed the highest correlation with CNC and CCC (Table 5).Water shortage reduced the biomass and LAI of maize[48],and sym 8 of the wavelet function was the most sensitive to CCC under water regimes.The relationship between wavelet functions and leaf carbon status was associated with wavelet property [34] and may be affected by the maize growth environment.Increased nitrogen promotes the synthesis of chlorophyll in maize leaves[49],and the red edge region was extremely sensitive to chlorophyll content.This is why the sensitive wavebands of CNC and CCC under nitrogen regimes extracted by the wavelet functions were in the red edge region. In many studies[20,50,51],VIs have been used to establish estimation models for crop nitrogen content.VIs of SDr/SDband FD742estimated wheat nitrogen status under various cultivation conditions[52],broad wavebands with low accuracy were used to calculate these VIs,a practice that was not conducive to the extraction of sensitive wavebands and practical ground monitoring applications[21].In the present study,high-precision spectral wavebands were used to calculate the VIs of two-by-two combinations.Datasets acquired under multiple cultivation environments were analyzed separately to estimate CNC and CCC using VIs.The CNC and CCC estimation models showed stable modeling and verification accuracy.NDVI of one study based on the red edge and NIR wavebands was better than the optimized red edge absorption area index based on the red edge and green wavebands for estimating LNC[53],showing superior estimation performance.High signal-to-noise ratio spectral wavebands were removed,and the interference of watersensitive wavebands for CNC and CCC estimation models was ignored in developing the VIs.Because water-sensitive wavebands would interfere with the estimation of the CNC and CCC,the CWT method was used to remove the water spectrum [12],increasing the calculation workload of the model and weakening the ability to estimate CNC and CCC.Under water regimes,higher R2was observed for the exponential function of CCC with the expression(SDr-SDb)/(SDr+SDb).The highest prediction accuracy of soybean LCC was obtained with the expression (SDr-SDy)/(SDr+SDy) [9],indicating that the VIs of the red edge area with the derivative spectra are helpful for estimation of leaf carbon status. Net primary productivity(NPP)is an indicator used to evaluate vegetation ecosystems and carbon cycling [54].Satellite remote sensing,such as by MODIS and Landsat,is often used to estimate NPP on a large scale or even globally [55,56].However,it was difficult to accurately assess the terrestrial carbon cycle from high-altitude satellite images using NDVI [57].The modeling and evaluation of NPP were more complex than those of CCC,and meteorological factors weakened the reliability of the NPP model.In the present study,VIs were used to achieve superior estimation performance for maize CCC,directly monitor carbon status in the field,and provide data support for diagnosing large-scale carbon status. The validation results illustrated that the CWT method is superior to VIs in the dimensionality reduction and optimization of spectral reflectance data.The PLS regression models were stable and showed reliable performance (with the lowest RMSE) in estimating maize leaf carbon and nitrogen status.A previous study[44] also demonstrated that the prediction accuracy of linear and random forest regressions was slightly inferior to that of PLS regression.However,PLS regression models contained more spectral parameters,resulting in more complex and slower operations.On the one hand,more spectral information increases the risk of overfitting[38];on the other hand,loss of valid information inevitably affects the stability of the models [34]. Fig.10.Standardized regression coefficients of UVE-PLS for CNC and CCC estimation under water and nitrogen regimes.(A)and(B)indicate respectively CNC and CCC under water regimes.(C) and (D) indicate respectively CNC and CCC under nitrogen regimes.DVI,difference vegetation index;RVI,ratio vegetation index;NDVI,normalized difference vegetation index;GNDVI,green normalized difference vegetation index;(SDr -SDb)/(SDr+SDb),the normalized value of red and blue edge areas;(SDr -SDy)/(SDr+SDy),the normalized value of red and yellow edge areas.(For interpretation of the references to color in this figure legend,the reader is referred to the web version of this article.) Each variable undeniably influenced the PLS model,but uninformative variables impair models and weaken their prediction performance [58].When the UVE program was run,several artificial random variable matrices were generated,resulting in the calculation of several thresholds for selecting informative spectral parameters (Table S3).The magnitude of the threshold had no obvious relationship with the uninformative variables and the prediction accuracy of the PLS regression model,because the calculated artificial random variable matrices were independent.Standardized regression coefficients are often used to indicate the importance of corresponding spectral parameters [59].The higher the absolute value of the standardized regression coefficient,the more noticeable was the influence of the spectral parameters on the model.We plotted the standardized regression coefficients of UVE-PLS with the highest prediction accuracy for CNC and CCC (Fig.10).RVI and NDVI were always selected,especially in terms of nitrogen regime,and RVI and NDVI generally corresponded to high absolute values of standardized regression coefficients and greatly contributed to the PLS regression model.Under water regimes,the sym8 of the wavelet function was the most contributive to the PLS model of CNC and CCC.In calculating the correlations between wavelet coefficients and CNC and CCC,we found that sym 8 showed positive correlations with CNC and CCC(Table 5),and RVI and NDVI showed positive correlations with CNC and CCC (Table 4).Given that the standardized regression coefficients were vector values,the value of the standardized regression coefficient can reflect a positive or negative correlation of spectral parameters with CNC and CCC in the PLS regression model.However,correlation analysis describes the correlation between two quantitative variables.For the PLS regression analysis,owing to the influence of the newly added variables (spectral parameters)on the dependent variable(CNC or CCC),the value of the standardized regression coefficients might change.We could not judge whether the spectral parameters were positively or negatively correlated with CNC and CCC.For example,DVI and CNC were positively correlated under water regimes,but the standardized regression coefficient showed a negative value because other spectral parameters participated in the PLS regression analysis and changed the vector values.Additionally,variables with very low absolute values of standardized regression coefficients and their contributions tended to cancel out [59].Standardized regression coefficients were used to select relevant variables to establish PLS regression models [60].Thus,the prediction accuracy of PLS regression models was collectively determined with informative spectral parameters and the magnitude of standardized regression coefficients.No obvious relationship of variable selection with stress conditions (water and nitrogen) has been found. The predicted and measured values of CNC and CCC under nitrogen regimes showed clustering in scatterplots (Fig.9B and D).We analyzed the reason for this clustering in scatterplots,as shown in Fig.11.Two reasons may have caused it:First,the validation dataset was sampled in few growth stages(V6 and R2 stages).The sampling intervals between the two stages were too long.Second,before the V6 stage of maize,the plant’s nitrogen absorption and utilization rate were low,and dry matter accumulation was slow,resulting in low canopy carbon and nitrogen content.However,after the V6 stage,more nitrogen fertilizer promoted the rapid growth of maize plants,and dry matter accumulation and nitrogen accumulation increased.Thus,canopy carbon and nitrogen contents at the R2 stage were increased,and were much higher than at the V6 stage.Although the clustering in scatterplots appeared under nitrogen regimes,the values were relatively evenly distributed on both sides of the 1:1 line.The R2of the models did not decrease as a result.However,the RMSE of models was increased owing to the clustering of the data. Drought in maize would reduce nitrogen absorption and dry matter accumulation at the V6 and R2 stages.During drought stress,maize plants were sheltered from the rain in automatically controlled rain shelters,and insufficient light further slowed the growth and development of plants.Finally,canopy carbon and nitrogen contents were slightly higher at the R2 stage than at the V6 stage.Although the sampling interval between the two stages was too long,there was no data clustering phenomenon.We infer that more growth stages should be considered for the enrichment of validation data.Optimizing and adjusting the sampling intervals are essential for improving the accuracy of the model.The field experiment for nitrogen regimes in this study involved two maize cultivars.The difference between the cultivars in the calibration and validation datasets may account for some errors.In contrast,only one cultivar was tested in the field with multiple water regimes.More maize cultivars should be used to evaluate CNC and CCC estimation models in future. Fig.11.Maize CNC(A)and CCC(B)at V6 and R2 stages for validation dataset(Exp.1 and Exp.2).WW,well-watered;MD,mild drought;ID,intermediate drought;SD,severe drought;N1,60 kg ha-1;N2,120 kg ha-1;N3,240 kg ha-1. In this study,CNC and CCC estimation models under water and nitrogen regimes were more accurate when established separately.These models can be used by agronomists to estimate the nitrogen and carbon content of maize.However,it is difficult to apply these estimation models to evaluating field water and nitrogen levels in practical production.Future research should be performed to test the estimation models with independent datasets,increasing their reliability and stability under a range of water and nitrogen regimes.It is possible that canopy water content or nitrogen nutrition index can help to evaluate field water and nitrogen levels.At the same time,we need to separate water from nitrogen nutrition levels and develop models that will yield more accurate diagnosis of water and nitrogen levels.The Sichuan region has a unique subtropical monsoon climate with overcast and rainy conditions that can interfere with the collection of spectral reflectance data.Thus,the application of the model is restricted by region.Development of a calibration formula might standardize spectral reflectance data and estimation models influenced by climatic conditions. Canopy hyperspectral reflectance effectively monitored the nitrogen and carbon status of maize crops and provided information for determining appropriate nitrogen fertilizer and precision management approaches in the field.VIs and wavelet functions were correlated with CNC and CCC under water and nitrogen regimes.VIs and wavelet functions accomplished the extraction of sensitive wavebands from canopy spectral reflectance in the 350-1000 nm spectral range,distributed mainly in the red edge and NIR regions.Under water and nitrogen regimes,the PLS regression models for CNC and CCC yielded prediction accuracy superior to that of linear and nonlinear models.To improve the prediction accuracy of the models and simplify the estimation models,we validated the UVE-PLS regression models of CNC and CCC,resulting in the highest accuracy under water and nitrogen regimes.We conclude that UVE is a reliable and stable method for establishing PLS regression models to estimate the CNC and CCC of maize under water and nitrogen regimes.In future,datasets from more cultivars and growing regions should be used for evaluating the robustness of UVE-PLS regression models for CNC and CCC estimation. CRediT authorship contribution statement Zhonglin Wang:Conceptualization,Data curation,Investigation,Writing -original draft.Junxu Chen:Data curation,Formal analysis,Investigation,Software.Jiawei Zhang:Data curation,Investigation,Methodology,Validation.Xianming Tan:Data curation,Formal analysis,Investigation.Muhammad Ali Raza:Investigation,Writing -review &editing.Jun Ma:Resources,Writing -review &editing.Yan Zhu:Resources,Writing -review&editing.Feng Yang:Conceptualization,Project administration,Writing -review &editing.Wenyu Yang:Resources,Supervision. Declaration of competing interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Acknowledgments The research was supported by the National Key Research and Development Program of China(2016YFD0300602),China Agricultural Research System (CARS-04-PS19),and Chengdu Science and Technology Project (2020-YF09-00033-SN). Appendix A.Supplementary data Supplementary data for this article can be found online at https://doi.org/10.1016/j.cj.2021.12.005.
2.4.Data application

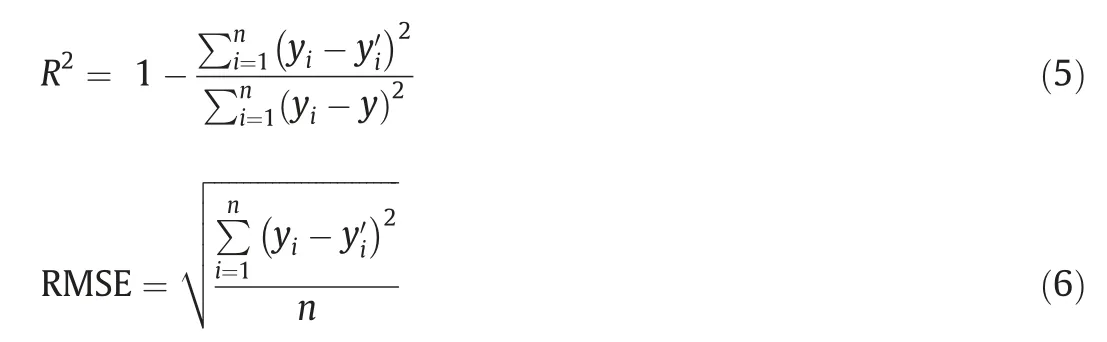
3.Results
3.1.Relationship of VIs with CNC and CCC
3.2.Relationship of wavelet coefficients with CNC and CCC
3.3.Accuracy of CNC and CCC monitoring with VIs and wavelet coefficients
3.4.Validation of estimation models of CNC and CCC


3.5.Variable selection and prediction accuracy of the UVE-PLS regression models
3.6.Validation accuracy of the UVE-PLS regression models for CNC and CCC

4.Discussion
4.1.Sensitive wavebands of CNC and CCC using VIs and wavelet functions
4.2.Estimation of CNC and CCC based on spectral parameters
4.3.Selection and importance of informative spectral parameters for UVE-PLS regression models
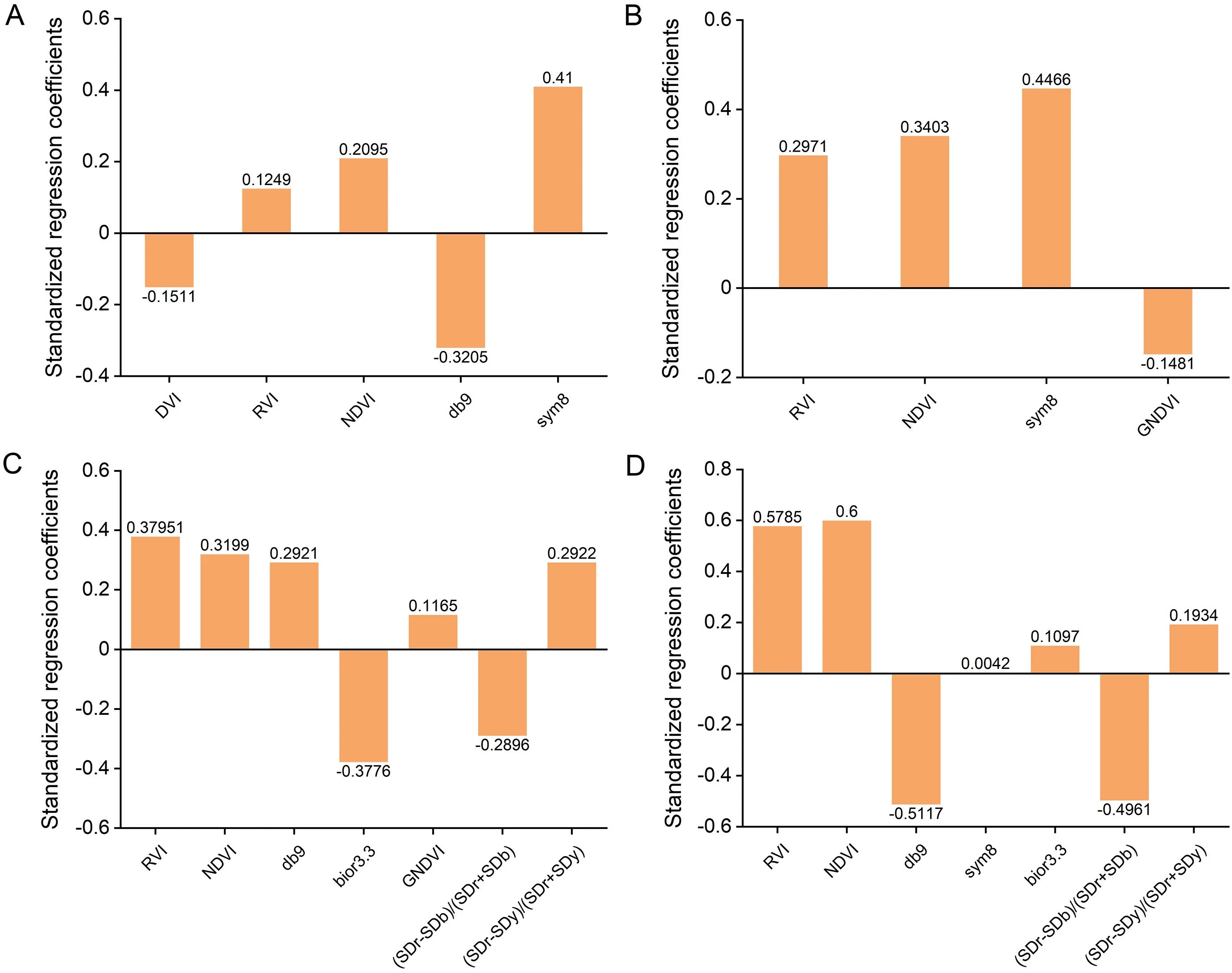
4.4.What is the reason for clustering in scatterplots?
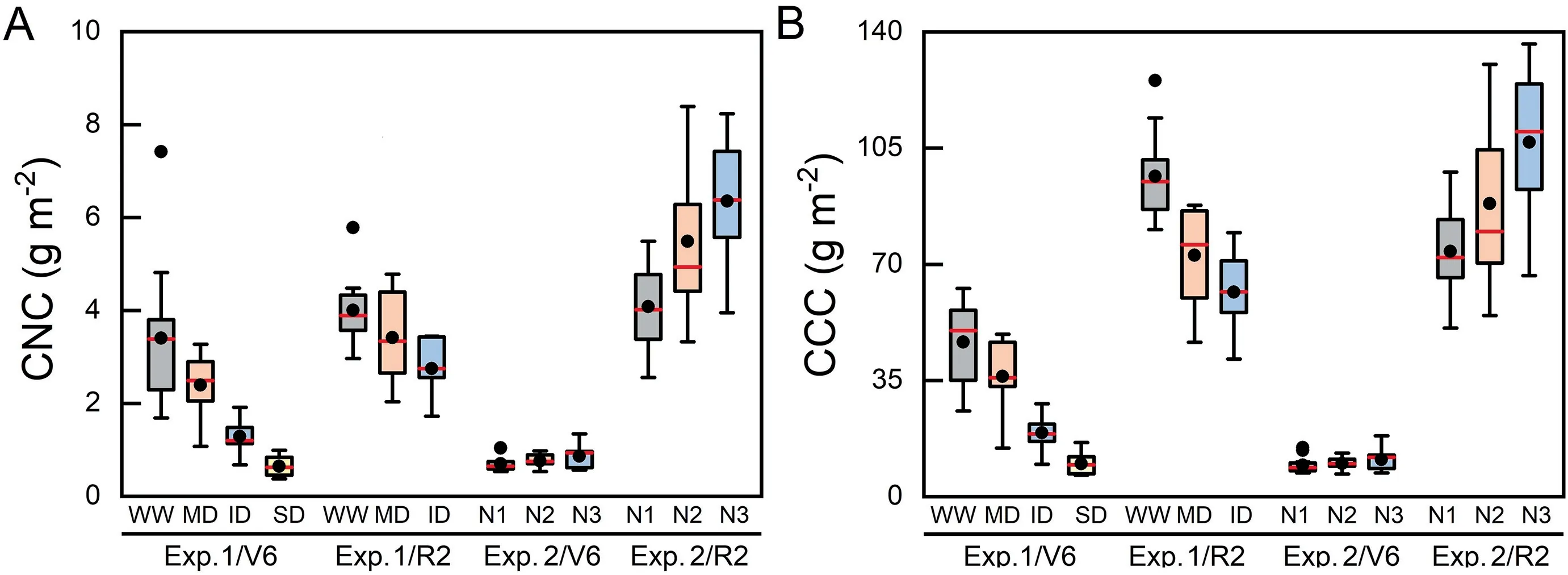
4.5.Model application and challenges
5.Conclusions
- The Crop Journal的其它文章
- Automatic segmentation of stem and leaf components and individual maize plants in field terrestrial LiDAR data using convolutional neural networks
- Leaf pigment retrieval using the PROSAIL model:Influence of uncertainty in prior canopy-structure information
- The continuous wavelet projections algorithm: A practical spectral-feature-mining approach for crop detection
- Field estimation of maize plant height at jointing stage using an RGB-D camera
- Quantifying the effects of stripe rust disease on wheat canopy spectrum based on eliminating non-physiological stresses
- Estimation of spectral responses and chlorophyll based on growth stage effects explored by machine learning methods

