Eu2+掺杂A2CaPO4F(A=K,Rb)格位占据和发光性质的第一性原理研究
乔 政,马 健,营 逍,宁利新
(安徽师范大学 物理与电子信息学院,安徽 芜湖 241000)
1 引 言
高效稳定可控的新型发光材料的研发一直是业界关注的焦点[1-5]。最近,A2CaPO4F∶Eu2+(A=K,Rb)荧光粉由于出色的发光性能和应用前景而受到广泛关注[6-10]。特别是组分可变RbxK2-xCaPO4F∶Eu2+荧光粉,在单一波长(380 nm)的近紫外光激发下,其发射光谱随着组分变化可覆盖整个可见光区域,从而实现发光颜色调控。尽管研究人员已从实验角度对其晶体结构和发光性能进行了大量研究,但由于发光中心Eu2+离子占据相应格位时存在电荷补偿的情况,其确切的占位情况仍有待进一步确认。荧光粉的发光性质在很大程度上取决于发光中心配位环境,为进一步精准调控光谱和优化荧光粉发光性能,准确了解荧光粉中发光中心离子格位占据情况及发光离子占据格位局域结构就显得尤为重要[11-16]。
在通过掺杂离子实现发光的荧光粉中,由于掺杂离子的价电子数、离子半径等与基质中被替代的原子不同,在掺杂时会引起基质晶体结构畸变。尤其当掺杂离子价电子数与基质中被替代的离子价电子数不同时,为了使整个晶体保持电中性,需要进行电荷补偿。在没有共掺杂电荷补偿离子时,会形成与掺杂离子占据格位电荷相反的缺陷,如空位缺陷、反位缺陷等。电荷补偿造成的缺陷会改变发光格位局域结构,从而改变荧光粉发光性质。电荷补偿的多样性和不确定性增加了实验上研究发光机理的难度。A2CaPO4F∶Eu2+(A=K,Rb)荧光粉就是这种情况,基质晶体中有碱金属(K/Rb)和碱土金属(Ca)两种格位可供Eu离子占据。当正二价的Eu离子占据碱金属离子格位时,多出了一个正电荷。此时其电荷补偿途径可以是碱金属离子空位(V′K/V′Rb,使用Kröger-Vink符号标记缺陷[17])、碱金属离子取代碱土金属离子(K′Ca/Rb′Ca)、O取代F(O′F)等。而相同电荷补偿还可能在晶体中出现不同分布情况,因此在实验上很难准确阐明发光机理,确定发光格位局域结构。而这时可以用DFT第一性原理计算来帮助解决问题[18-20]。
Rb2CaPO4F晶体属于正交晶系,Pnma点群(No.62),有两个9配位Rb格位(RbO7F2)和一个6配位Ca格位(CaO4F2)[8-10,21]。在先前Daicho和Li等的文章中认为K2CaPO4F属于单斜晶系,P21/m点群(No.11),有4个9配位的K格位(KO7F2)和两个6配位的Ca格位(CaO4F2)[6-7]。但由于其倾斜角度很小(90.22°~90.32°),Ca1/Ca2格位配位结构相似,K1/K2格位配位结构相似,K3/K4格位配位结构相似,且400 K时,K2CaPO4F会发生相变,转变为正交晶系。最近,Cai、Wang和Wu等的实验文章认为其与Rb2CaPO4F一样属于正交晶系,Pnma点群(No.62)[8,10,21]。本文通过DFT计算发现,对于单斜晶系的K2CaPO4F,Eu2+占据Ca1和Ca2格位的缺陷形成能十分接近,且正交晶系的K2CaPO4F在能量上比单斜晶系更稳定。为与最近实验文章保持一致,本文将K2CaPO4F作为正交晶系处理,如图1所示。
本研究工作采用以超单胞模型为基础的密度泛函理论,对A2CaPO4F∶Eu2+(A=K,Rb)体系不同电荷补偿机制下的缺陷形成能进行计算,并根据缺陷形成能计算结果,利用SCF自洽场(ΔSCF)结合限制性布居方法对发射光谱进行格位指认[22-25]。在此基础上,还对Eu2+占据格位的基态及激发态配位环境和电子结构进行分析,讨论了配位环境与光谱之间的联系,并对实验观察到的现象进行解释。期望本文计算结果可以为实验上进一步优化类似荧光粉的发光性能提供参考。
2 计算方法
对A2CaPO4F(A=K,Rb)晶体采用2×2×1超单胞进行模拟,超单胞中含有16个Ca原子、32个A原子(A=K,Rb)、16个P原子、16个F原子和64个O原子,共144个原子。利用Vienna Ab-Inito Simulation Package(VASP)软件包,采用广义梯度近似下的Perdew-Burke-Ernzerhof(GGA-PBE)泛函进行周期性DFT计算,采用PBE+U(U=2.5 eV)方法处理Eu-4f电子[26-30]。在计算中,Ca原子3s23p64s2组态中电子、K原子3s23p64s1组态中电子、Rb原子4s24p65s1组态中电子、P原子3s23p3组态中电子、F原子2s22p5组态中电子、O原子2s22p4组态中电子及Eu原子4f75s25p66s2组态中电子被作为价电子处理。价电子与离子实之间相互作用使用投影扩充波(PAW)方法描述[31]。使用共轭梯度算法进行晶体构型优化,收敛能量设为10-6eV,作用在每个原子上的Hellmann-Feynman力大小设置为小于0.1 eV·nm-1。考虑到采用的超单胞含有原子个数较多,在布里渊区积分中只用一个k点Γ采样,并且将平面波截断能设置为420 eV以确保计算收敛。
缺陷形成能大小能够直接反映特定缺陷形成的难易程度或缺陷体系稳定性。电中性缺陷的缺陷形成能ΔEf可以表示为:
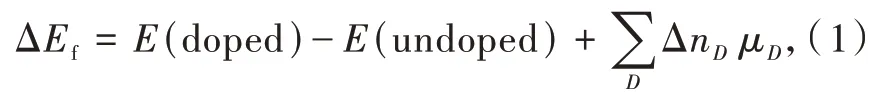
E(doped)和E(undoped)分别是掺杂晶体和未掺杂晶体的超单胞总能量。ΔnD是掺杂晶体相对于未掺杂晶体移除或添加D(=Ca,Rb,K,P,Eu,O,F)原子的个数(移除时,ΔnD>0;添加时,ΔnD<0)。μD是相应D原子的化学势。
在热力学平衡条件下,公式(1)中的原子化学势μD满足下面的关系式:
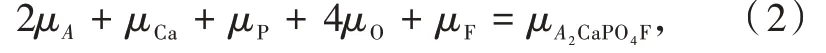
其中μA2CaPO4F为A2CaPO4F(A=K,Rb)晶体中每个化学式单元对应的总能量。考虑到材料合成的还原条件,对D=Ca,Rb,K,P,Eu时,可用体相金属中单原子能量近似表示μD的值。即用与上述相同收敛标准和16×16×16 k点网格计算得到Rb、K、P、Eu(双原子晶胞)和Ca(单原子晶胞)的能量。
在K2CaPO4F中,μF和μO可由以下关系式得到:
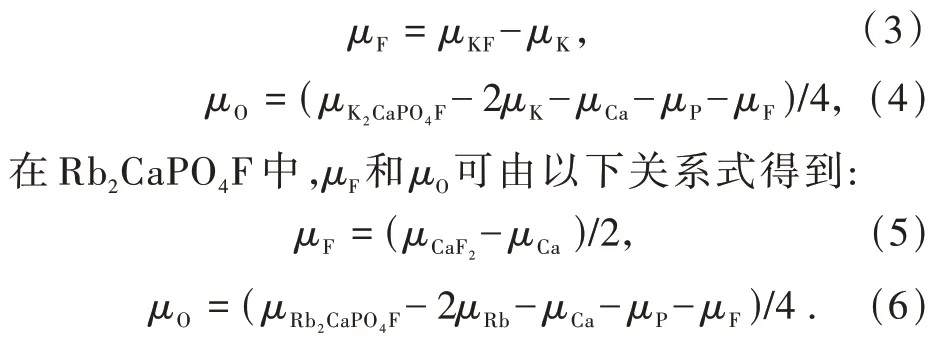
采用ΔSCF结合限制性布居方法计算光学跃迁能量。对于2~5 eV范围内的光学跃迁,该方法计算得到的跃迁能量与实验值相比误差通常在0.3 eV以内,可以对发射峰进行有效指认[32-33]。通过移去Eu2+能量最高的一个基态4f电子,同时在Eu2+能量最低的5d轨道上填充一个电子的方式得到激发态构型(设置5d电子与4f电子自旋方向相同),并对激发态构型进行完全结构弛豫。对光学跃迁能量的计算,遵循Frank-Condon原理,如图2所示[34-37]。即通过计算基态平衡构型(Q0)下激发态(E)和基态(G)的总能量差得到吸收光能量(Eabs);通过计算弛豫后的激发态平衡构型(Q0+ΔQ)下的激发态(E*)和基态(G*)总能量差得到发射光能量(Eem),具体关系式如下:
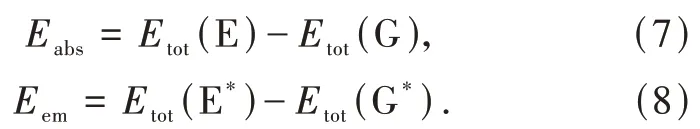
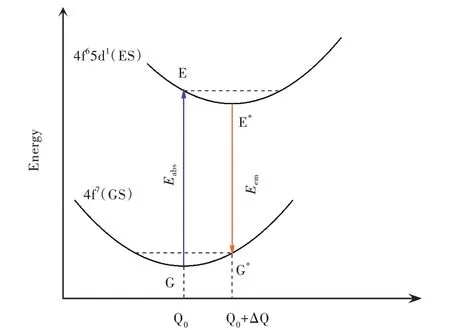
图2 光学吸收和发射能量的位形坐标原理示意图Fig.2 Schematic configuration coordinate diagram illustrating the calculated optical absorption and emission energies
3 结果与讨论
3.1 格位占据
为了得到Eu2+在A2CaPO4F(A=K,Rb)中的格位占据情况,使用PBE+U(U=2.5 eV)泛函对不同电荷补偿方式下Eu2+占据在A2CaPO4F(A=K,Rb)的Ca、A格位的缺陷形成能进行计算,结果如图3所示。
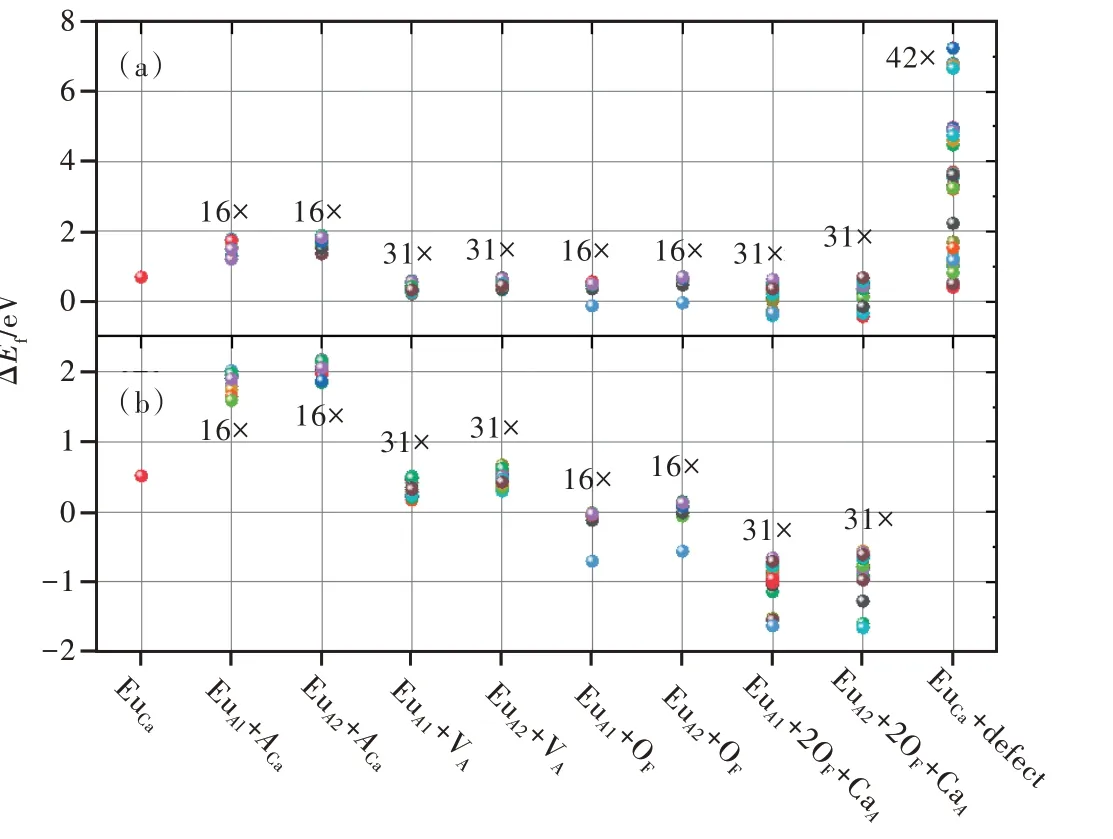
图3 计算得到的Eu2+在K2CaPO4F(a)和Rb2CaPO4F(b)不同格位占据方式的缺陷形成能(ΔEf)。图中还标注了Ω×来表示每种占据方式计算的构型数量。Fig.3 Calculated defect formation energies(ΔEf)for symmetrically distinct substitutions in K2CaPO4F(a)and Rb2CaPO4F(b).The number of configurationΩ×for each substitution is denoted.
由于Eu2+占据A格位时电荷不匹配,考虑了Eu·A+V′A、Eu·A+A′Ca、Eu·A+O′F和Eu·A+2O′F+Ca·A这四种组合方式进行电荷补偿。对于Eu·A+V′A这一组合,对Eu占据A1或A2格位时其他31个A原子格位依次出现V′A空位缺陷的情况全部进行 了 计 算,共 计 算 了124种 构 型。对Eu·A+A′Ca这一组合,计算了Eu占据A1或A2格位、同时16个Ca原子格位依次被A原子所取代的情况,共64种 构 型。对Eu·A+O′F这 一 组 合,计 算 了Eu占据A1或A2格位、同时16个F原子依次被O原子取代作为电荷补偿的情况,共64种构型。除上述三种电荷补偿方式外,还特别计算了Eu·A+2O′F+Ca·A这 一 组 合,即Eu占 据A原 子 格 位,与 其配位的2个F原子全部被O原子取代,同时一个Ca原子占据A原子格位作为电荷补偿。对Eu占据A1或A2格位,计算了其余31个A原子依次被Ca所取代的情况,共124种构型。
为了更好地解释计算结果,图4给出了A2Ca-PO4F(A=K,Rb)中A原子格位和F原子格位位置关系示意图。在晶体中,每个F原子格位分别与2个A1原子格位和2个A2原子格位配位。图4中,A11、A12、A13分 别 表 示3个 不 同A1原 子 格 位;A21、A22、A23分别表示3个不同A2原子格位。缺陷形成能计算结果表明,对于K2CaPO4F∶Eu2+,能量上最为稳定构型为Eu·K11+2O′F+Ca·K1(2Eu·K11+2O′F+Ca·K13)和Eu·K22+2O′F+Ca·K12(Eu·K22+2O′F+Ca·K13),其 次为Eu·K22+2O′F+Ca·K11、Eu·K11+2O′F+Ca·K22、Eu·K11+2O′F+Ca·K21(Eu·K11+2O′F+Ca·K23),接 着 为Eu·K22+2O′F+Ca·K21(Eu·K22+2O′F+Ca·K23)、Eu·K11+O′F和Eu·K22+O′F。这 里 所有OF缺陷均与Eu占据格位相邻。而其他构型缺陷形成能较高,出现几率很低。对于Rb2CaPO4F∶Eu2+,能量上最为稳定构型为Eu·Rb22+2O′F+Ca·Rb11和Eu·Rb11+2O′F+Ca·Rb22,即作为电荷补偿的Ca·Rb缺陷与两个O′F缺陷都相邻。而在K2CaPO4F中,能量最稳定构型的Ca·K缺陷只与一个O′F缺陷相邻。
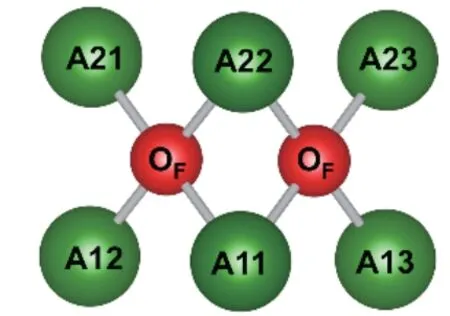
图4 晶体中A(A=K,Rb)原子格位和F原子格位位置示意图Fig.4 Schematic position diagram of A(A=K,Rb)sites and F sites in crystal
使用ΔSCF方法对缺陷形成能最低的几种构型的激发和发射光能量进行计算。计算结果如表1所示。对于K2CaPO4F∶Eu2+,显然实验上观察到的较强的662 nm(1.87 eV)发光峰和较弱的565 nm(2.20 eV)发射峰都来自于Eu·K+2O′F+Ca·K的组合。电荷补偿CaK的位置不同造成发光能量的差异。而较弱的497 nm(2.49 eV)发射峰来自Eu·K+O′F的 组 合。对 于Rb2CaPO4F∶Eu2+,Eu·Rb22+2O′F+Ca·Rb11和Eu·Rb11+2O′F+Ca·Rb22对 应 其 位 于484 nm(2.56 eV)附近的主发射峰,而在主发射峰长波方向的较弱发光为Eu·Rb22+2O′F+Ca·Rb12和Eu·Rb11+2O′F+Ca·Rb21等构型产生。
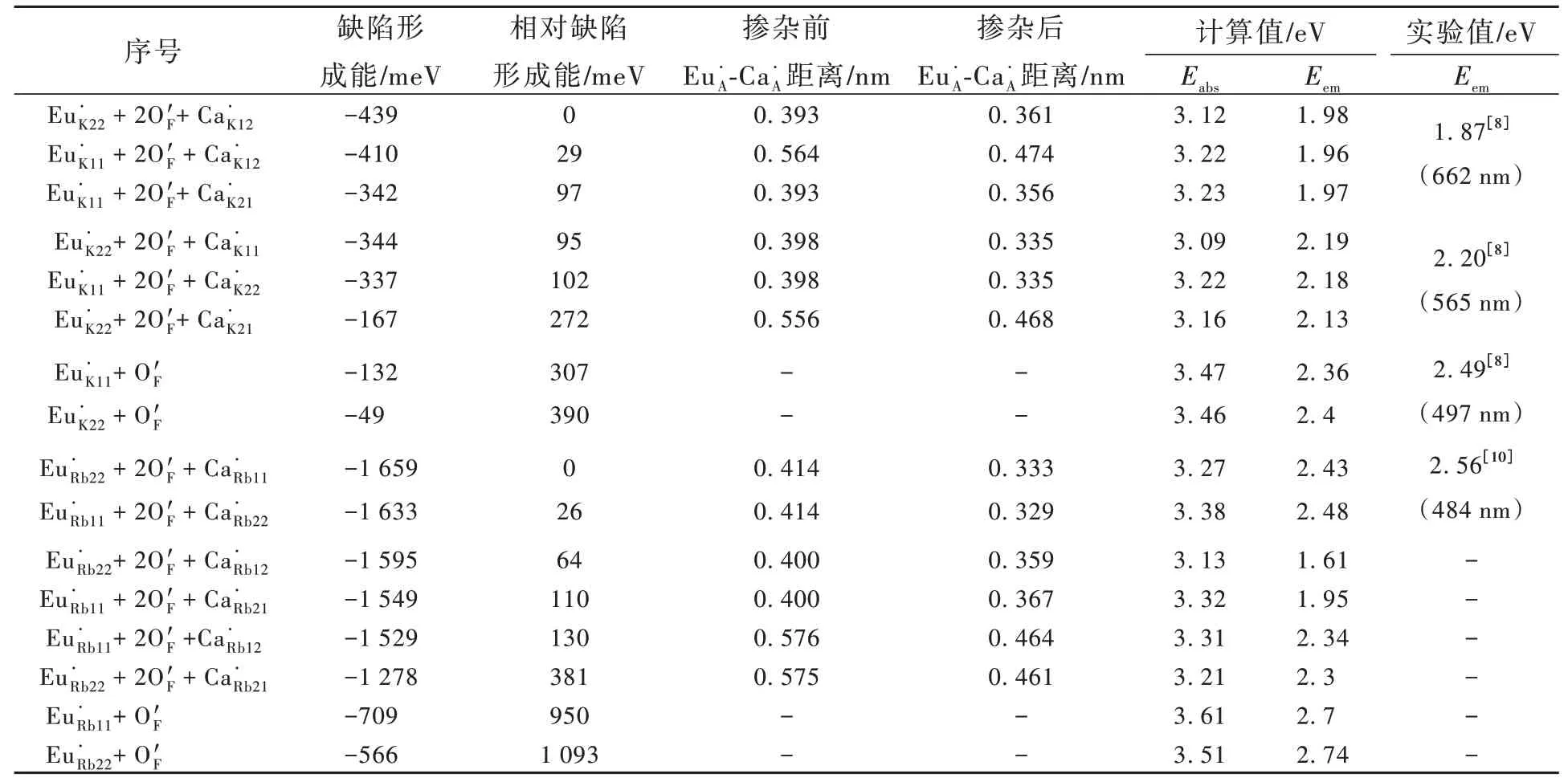
表1 A2CaPO4F∶Eu2+(A=K,Rb)缺陷形成能和光学跃迁能量计算值Tab.1 Calculated defect formation energies and optical transition energies in A2CaPO4F∶Eu2+(A=K,Rb)
考虑到Ca格位也有两个F原子与其配位,为进一步研究在K2CaPO4F∶Eu2+中Eu2+占据Ca格位的可能,对Ca格位相邻F原子或O原子被替代的情况 进行计算。共考虑了EuCa+O′F+Ca·K、EuCa+O′F+F·O、EuCa+2O′F+2Ca·K、EuCa+2O′F+2F·O、EuCa+F·O+O′F、EuCa+F·O+V′K、EuCa+F·O+K′Ca这7种情况。考虑到超单胞中O原子均位于PO4多面体内,F原子很难占据O格位,且Eu2+占据Ca格位不存在电荷不匹配的情况,所以并未计算所有该类构型,而是按Eu2+占据格位和电荷补偿距离最近、适中、最远的原则,对每种组合取6个与EuCa距离不同的电荷补偿构型作为代表,共计算了42种不同构型。计算结果示于图3(a),其能量最低的缺陷形成能相比Eu·K22+2O′F+Ca·K12构型高842 meV,在实验上很难观察到其发光。
基于PBE+U泛函优化得到的K2CaPO4F∶Eu2+的全部231种构型和Rb2CaPO4F∶Eu2+的全部189种构型的超单胞晶格参数如图5所示。掺杂前后a、b、c三个方向上的晶格参数误差分别不超过0.86%(0.53%)、0.59%(0.33%)和0.60%(0.73%),这说明Eu2+掺杂及相关电荷补偿对超单胞晶格变化的影响可以忽略[38-39]。
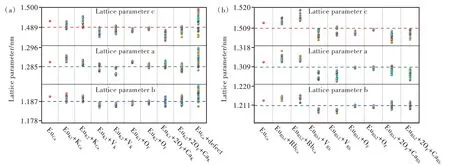
图5 计算得到的Eu2+在K2CaPO4F(a)和Rb2CaPO4F(b)不同格位占据方式下的晶格参数,图中虚线表示未掺杂晶体的晶格参数。Fig.5 Calculated lattice parameters for symmetrically distinct substitutions of Eu2+in K2CaPO4F(a)and Rb2CaPO4F(b).The lattice parameters of the undoped crystal are denoted with dashed line.
3.2 局域结构
荧光粉的发光性能在很大程度上取决于发光中心配位环境,在确定A2CaPO4F∶Eu2+(A=K,Rb)的格位占据情况后,接下来对Eu2+占据格位的局域结构进行简单分析。
图6(a)为DFT计算得到的Eu·K11+2O′F+Ca·K12构型的Eu2+占据格位局域结构,对应于662 nm发射峰。基态平衡构型下两个Eu—OF键长相对未掺杂时有明显收缩,这可归因于Eu2+与O2-之间有效正负电荷比K+与F-之间的更大,从而增大了静电引力。同时由于补偿电荷Ca·K与O′F10相邻,Eu—OF10键长收缩程度较Eu—OF4略小,这也是Ca2+与O2-之间静电吸引比K+与O2-之间更大的缘故。因为补偿电荷Ca·K到O′F10的距离与Ca·K到O′F4的距离不同,导致整个Eu·K11+2O′F+Ca·K12的配位结构呈各向异性变化,从而增强了晶体场分裂。而激发态平衡构型下,Eu占据格位进一步扭曲,不同Eu—O键长的变化幅度并不相同。这是由于Eu占据格位畸变较大,Eu处于偏离占据格位中心的位置,激发态下Eu-4f电子被激发到5d轨道使Eu离子半径增加,Eu向格位中心位置移动。这一过程会产生大的斯托克斯位移(Stokes shift)[40-42]。
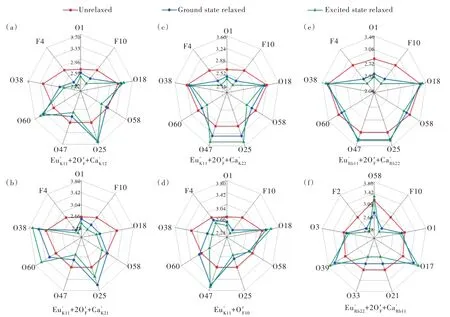
图6 DFT优化得到的Eu·K11+2O′F+Ca·K1(2a)、Eu·K11+2O′F+Ca·K2(1b)、Eu·K11+2O′F+Ca·K2(2c);Eu·K11+O′F10(d)、Eu·Rb11+2O′F+Ca·Rb2(2e)、Eu·Rb22+2O′F+Ca·Rb1(1f)取代格位的未掺杂、Eu2+的基态和激发态局域结构。Fig.6 Unrelaxed,relaxed ground-state,and relaxed excited-state local structures of Eu2+in the Eu·K11+2O′F+Ca·K1(2a),Eu·K11+2O′F+Ca·K2(1b),Eu·K11+2O′F+Ca·K2(2c),Eu·K11+O′F1(0d),Eu·Rb11+2O′F+Ca·Rb2(2e),and Eu·Rb22+2O′F+Ca·Rb1(1f)substitutions with the DFT method.
图6(b)为Eu·K11+2O′F+Ca·K21构型的Eu2+配位结构,与图6(a)相比,Eu—OF10键长略长,这可能是缺陷Ca·K所处K2格位的K—F键长比K1格位更短导致的。图6(c)为对应565 nm发射峰的Eu·K11+2O′F+Ca·K22构型Eu2+配位结构,相比图6(a)和图6(b),Eu占据后配位结构变化要规则得多。这是由于补偿电荷Ca·K到O′F4和O′F10的距离相同,占据格位的局域结构对称变化。这会产生较弱晶体场分裂,并抑制激发态弛豫,导致斯托克斯位移较小。图6(d)为对应497 nm发射峰的Eu·K11+O′F构型Eu2+配位结构。由于只有F10被O取代,F4未被取代,Eu·K11+O′F的配位结构发生了很强的扭曲,产生较强晶体场分裂。由于O2-取代F-可以提高晶体共价 性,可 以 预 期 在Eu·K11+O′F中,5d1权 重 能 级 位 移相对Eu·K+2O′F较小,从而 使Eu·K11+O′F中 的 激 发 光和发射光能量相比Eu·K+2O′F都有所增大。Eu占据K2格位的整体情况与Eu占据K1格位类似。
对于Rb2CaPO4F∶Eu2+,Eu占据格位局域结构与K2CaPO4F∶Eu2+类似。图6(e)、(f)给出了对应484 nm发射峰的Eu2+配位结构,此时缺陷Ca·Rb到两个O′F缺陷距离相等,Eu占据格位的局域结构呈现对称变化,产生较弱晶体场分裂和较小斯托克斯位移。
3.3 电子性质
了解晶体内的能带分布情况可以帮助理解荧光粉的发光行为。图7(a1)为使用PBE泛函计算得到的K2CaPO4F晶体的电子态密度图,把价带顶设置为导带则主要由Ca-d电子态构成。在费米能级之上约横坐标的0 eV位置。价带顶由O-p电子态主导,而4.46 eV处出现的小峰构成了导带边,主要由K-s电子态和O-s电子态杂化形成。Rb2CaPO4F晶体的电子态密度图的特征与K2Ca-PO4F十分相近(图7(b1)),价带顶同样是由O-p电子态主导,导带主要由Ca-d电子态构成。二者主要的差别在于,由Rb-s电子态和O-s电子态杂化形成的导带边的小峰比费米能级高4.52 eV,略大于K2CaPO4F中的情况。这说明在晶体中,K—O键的共价性略高于Rb—O键,使晶体中K—K间距(0.351 nm)比Rb—Rb间距(0.352 nm)略小,并由此导致K2CaPO4F的导带相比Rb2CaPO4F更宽,而带隙略小于Rb2CaPO4F[25]。
图7(a2)和7(a3)、图7(b2)和7(b3)分别为使用PBE+U泛函计算得到的K2CaPO4F∶Eu2+中出现几率最高的Eu·K22+2O′F+Ca·K12构型电子态密度图和Rb2CaPO4F∶Eu2+中出现几率最高的Eu·Rb22+2O′F+Ca·Rb11构型电子态密度图。在二者的基态,分别于3.24 eV和2.89 eV处出现由Eu-4f电子构成的小峰(图7(a2)、(b2))。而在基质价带顶上方,出现一些O-p电子态主导的连续的小峰,且在K2Ca-PO4F∶Eu2+中多于Rb2CaPO4F∶Eu2+中,这主要是由O′F缺陷产生的,K2CaPO4F∶Eu2+中更加离散的缺陷态分布表明了Eu·K格位附近更强的结构畸变。
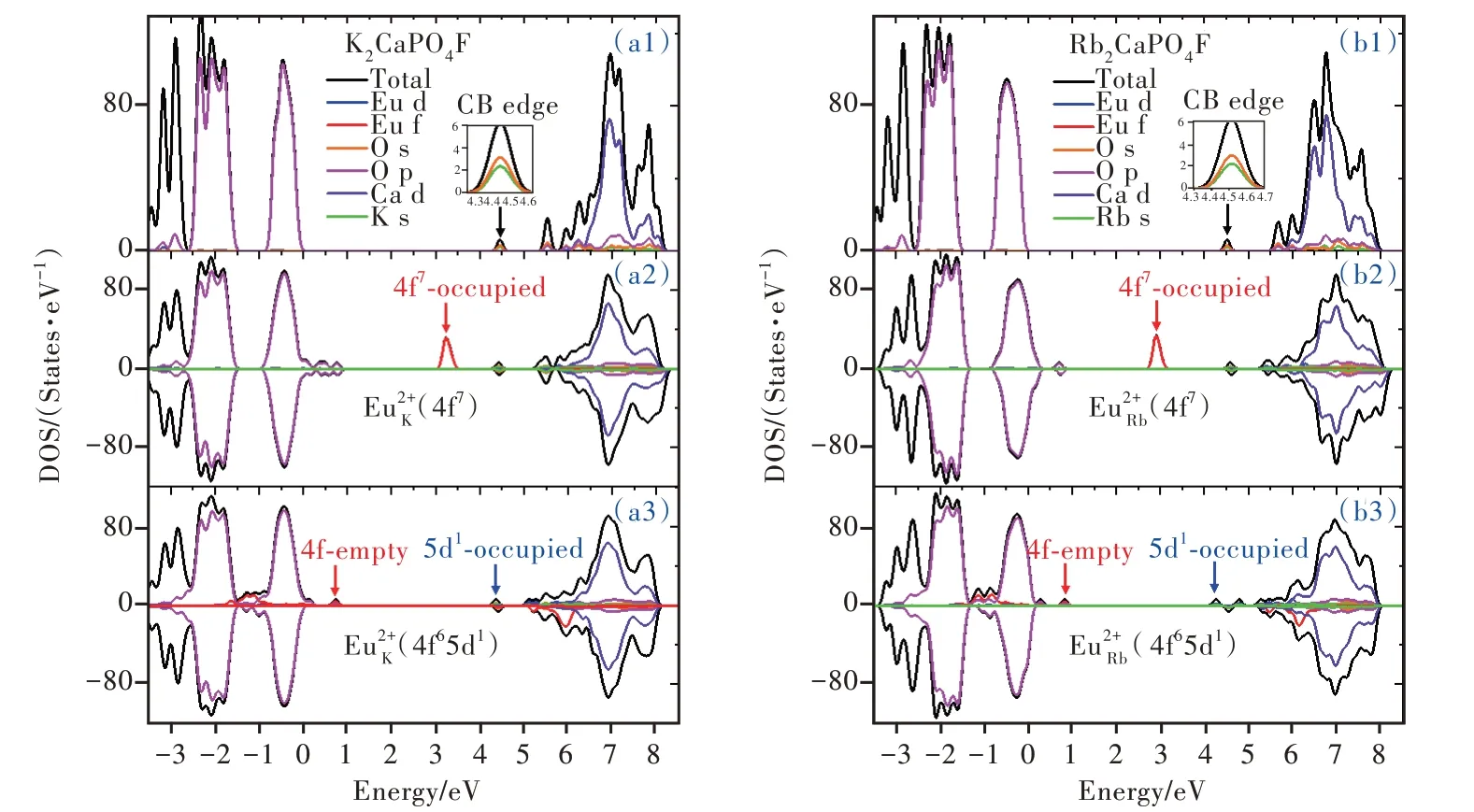
图7 DFT计算得到的未掺杂K2CaPO4F晶体(a1)、未掺杂Rb2CaPO4F晶体(b1)、Eu2+掺杂K2CaPO4F晶体(Eu·K22+2O′F+Ca·K12构型)((a2)~(a3))、Eu2+掺杂Rb2CaPO4F晶体(Eu·Rb22+2O′F+Ca·Rb11)((b2)~(b3))的总电子态密度和分波电子态密度。(a2)、(b2)基态构型下的Eu2+的4f7基态电子态密度;(a3)、(b3)激发态构型下的Eu2+的4f65d1激发态电子态密度。Fig.7 DFT-calculated total and orbital-projected DOSs for the pure K2CaPO4F crystal(a1),pure Rb2CaPO4F crystal(b1),Eudoped K2CaPO4F crystal in the most stable Eu·K22+2O′F+Ca·K12 substitution((a2)-(a3))and Eu-doped Rb2CaPO4F crystal in the most stable Eu·Rb22+2O′F+Ca·Rb11 substitution((b2)-(b3)).Eu2+in the 4f7 ground state with ground-state geometry in panel(a2)and(b2),Eu2+in the 4f65d1 excited state with excited-state geometry in panel(a3)and(b3).
在基态平衡构型下,利用DFT限制性布居方法,在Eu-4f轨道上加入一个空穴,同时在能量最低的Eu-5d轨道上放入一个电子,计算得到激发态电子态密度图,如图7(a3)、(b3)所示。此时分别在两个体系的4.36 eV和4.27 eV处出现由Eu-5d占据轨道占主导的小峰,而非占据的Eu-4f轨道靠近价带顶,占据的Eu-4f轨道进入价带。激发态下Eu-4f轨道和Eu-5d轨道能级位置相比基态时降低,是由于相比4f能级,5d能级离原子核更远。当4f电子被激发到5d轨道上时,对于5d轨道,有效核电荷数增大,导致5d轨道向下移动。对于4f轨道,外层的5d电子对其产生库伦斥力,同样降低了其轨道位置。
3.4 讨论
DFT计算结果表明,无论是K2CaPO4F∶Eu2+在660 nm附近的发光还是Rb2CaPO4F∶Eu2+在480 nm附近的发光,都是由Eu·K/Rb+2O′F+Ca·K/Rb这一格位占据组合产生的。发射光波长的巨大差异主要是因为电荷补偿缺陷Ca·K和Ca·Rb所处的位置不同。在K2CaPO4F∶Eu2+中,Ca倾向于占据只与一个O′F缺陷相邻的K格位,从而增加Eu占据格位的局域结构各向异性,使Eu极大地偏离了配位多面体的中心位置,增强了晶体场分裂,并产生了较大斯托克斯位移。而在Rb2CaPO4F∶Eu2+中,Ca倾向于占据与 两 个O′F都相邻的Rb格 位,对Eu占 据 格位的局域结构畸变相对影响较小,从而产生较弱的晶体场分裂,并抑制激发态弛豫,产生较小斯托克斯位移。
造 成K2CaPO4F∶Eu2+和Rb2CaPO4F∶Eu2+中 缺陷Ca·K和Ca·Rb所处位置不同的主要原因是Ca2+、Eu2+、K+、Rb+这四种离子的离子半径差异。相同配位数下,Ca2+离子半径最小,Rb+离子半径最大(6配位时,Ca2+0.100 nm,Eu2+0.117 nm,K+0.138 nm,Rb+0.152 nm)。而O2-的半径(4配位时为0.138 nm)大 于F-(4配 位 时 为0.131 nm)[43]。因 此 在Rb2CaPO4F∶Eu2+中,Ca·Rb只有与两个O′F都相邻,才能尽可能抵消Ca2+和Rb+较大离子半径差异造成的晶体结构畸变。
实验上发现对于K2CaPO4F∶Eu2+荧光粉,除了在660 nm附近存在发射峰,减小激发光波长,还可以在480 nm附近发现较强发光。根据DFT计算结果,这一发光中心对应的为Eu·K+O′F格位占据组合。尽管缺陷形成能计算结果表明,Eu·K+O′F的相对缺陷形成能比Eu·K+2O′F+Ca·K中最稳定的构型高约300 meV。但考虑到Eu·K+O′F的构型数量比Eu·K+2O′F+Ca·K更多(Eu·K+O′F构型简并度更高),同时对于在还原气氛中合成的实验晶体来说,Eu·K+O′F构型所需的O原子数量更少,更有利于在晶体中出现该类占据。而对于Rb2CaPO4F∶Eu2+,Eu·Rb+O′F相 对 缺 陷 形 成 能 比Eu·Rb+2O′F+Ca·Rb高 出超过950 meV,在实验上很难观察到相应发射峰。
在2019年Li等的文章中[7],实验人员发现不同合成温度得到的K2CaPO4F∶Eu2+荧光粉在360 nm波长光激发下发光性质不同。1 173 K和1 223 K温度下合成得到的晶体在660 nm(1.88 eV)附近发光较强,在480 nm(2.60 eV)附近发光很弱。但是1 273 K温度下合成得到晶体的660 nm和480 nm两个发射峰强度相当。这是由于合成温度较低时,缺陷形成能差异在Eu占据几率分布中发挥主导作用,缺陷形成能较低的Eu·K+2O′F+Ca·K的出现几率更高。合成温度升高后,形成能大小在Eu占据几率分布中的作用减小,而构型数量(简并度)在Eu占据几率分布中的作用增强,所以形成能较高,构型数量更多的Eu·K+O′F出现几率显著增加。同时还原气氛下,合成温度升高,会减少多余的O原子,使得Eu更多以Eu·K+O′F的方式占据。
4 结 论
为了明确A2CaPO4F∶Eu2(+A=K,Rb)荧光粉的格位占据情况及发光机理,本文采用DFT+U泛函对不同电荷补偿机制下的缺陷形成能进行计算,并根据缺陷形成能计算结果,结合ΔSCF方法,对发光中心进行格位指认。计算结果表明,Rb+和K+离子半径的差异导致发光格位第二配位层的Ca(·AA=K,Rb)缺陷分布倾向不同,进而影响发光性质。K2CaPO4F∶Eu2+的660 nm附近发射峰和480 nm附近发射峰都为Eu占据K格位所产生,前者的电荷补偿方式为与Eu占据格位配位的两个F原子都被O原子取代,且缺陷Ca·K与两个O′F缺陷中的一个相邻;后者的电荷补偿方式为与Eu占据格位配位的两个F原子中的一个被O原子取代。Rb2CaPO4F∶Eu2+的480 nm发光为Eu占据Rb格位所产生,其电荷补偿方式为与Eu占据格位配位的两个F原子都被O原子取代,且缺陷Ca·K与两个O′F缺陷都相邻。在格位指认的基础上,还对Eu占据格位基态与激发态配位环境及电子结构进行分析,发现K2CaPO4F∶Eu2+中Eu占据格位的剧烈局域结构畸变是斯托克斯位移增大的主要原因。同时揭示了实验上不同合成温度下得到的K2CaPO4F∶Eu2+发光性质不同的本质。期望本工作可以为实验上优化该类荧光粉的发光性能、精准调控光谱提供帮助。
本文专家审稿意见及作者回复内容的下载地址:http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220148.

