基于深度神经网络-近似线性网络混合模型的 电力系统状态估计方法

宋雨露， 樊艳芳， 刘雨佳， 刘牧阳， 白雪岩

(新疆大学电气工程学院， 乌鲁木齐 830017)

状态估计是能量管理系统的重要组成部分，它根据量测冗余度来降低量测误差，以期得到电网在该时刻的运行状态[1]。提高状态估计时效性和准确性有利于准确了解系统当前状态及其状态变化趋势、保证电力系统的安全性和经济性，可以预防停电事故。2020年，中国提出“2030年前实现碳达峰、2060年前实现碳中和”，构建以新能源为主体的新型电力系统，推动实现碳达峰、碳中和[2]。在电力系统升级改造的过程中，存在潮流分布的不确定性剧增、电网电压波动频发等问题，这些问题使得实时大规模电力系统状态估计(power system state estimation, PSSE)显得越来越重要。从其他方面来看，随着电网建设不断提速，智能化程度不断提高，数据采集系统的终端采集频率提高、数据误差减少，为状态估计提供了海量优质的数据集，为利用深度学习算法提供了数据基础[3]。

加权最小二乘(weighted least square, WLS)状态估计法和最小绝对值(weighted least absolute value, WLAV)状态估计法[4]是目前最常用的状态估计法。WLS状态估计法是线性估计，受异常值扰动影响大，且在求解过程中存在时效性差、精确性差、复杂度高等问题。利用神经网络强大的函数逼近能力，将传统高斯-牛顿(Gauss-Newton, G-N)算法中的迭代过程转化为神经网络的计算，提高了速度和精度[5]。文献[6-7]提出了利用前馈神经网络(feedforward neural network, FNN) 实现电力系统的状态估计的方法，即使用历史数据和模拟样本数据对模型进行离线训练，完成训练的FNN模型就可以实现电力系统的实时状态估计，训练过程中系统参数向量矩阵只需要进行有限次的运算，就可以得到比较理想的结果；但是该方法没有考虑数据精度不高和数据缺失的影响，也没有针对模型隐藏层数的增加问题进行探讨。Mestav等[8]提出了一种贝叶斯状态估计器，将贝叶斯准则与深度神经网络相结合，并实现了实时的网络状态的最小平均平方误差估计；但该估计器的鲁棒性较差。Haday等[9]提出了一种联合卷积神经网络(convolutional neural network, CNN)和循环神经网络(recurrent neural network, RNN)混合模型的电力系统状态估计方法。该方法利用 CNN估计电压幅值，利用RNN估计电压相角；但由于RNN是根据时间序列进行分析的，CNN则没有这个预设条件，故两者分别产生估计结果的统一化是一个新的问题。

综上，基于神经网络的电力系统状态估计方法还有很大的发展空间。为提高电力系统实时状态估计的精度和计算效率，实现从传统的物理建模方式向“物理建模+数据驱动”方式的转变，现提出一种基于深度神经网络-近似线性网络(deep neural network-proline network, DNN-PN)模型的电力系统状态估计方法。该方法首先利用数据采集与监控系统(supervisory control and data acquisition，SCADA)系统和相量量测单元(phase measurement unit, PMU)生成混合历史量测数据；然后将数据通过粒子滤波算法，利用序列重要性重采样，生成总的样本集，其中80%作为训练样本用以离线训练DNN-PN混合网络模型；最后将另外20%作为测试样本输入已建立的模型中，通过前向传播和反向计算获得系统状态估计的结果，并通过仿真实验验证在实时状态估计的精度和计算效率。

1 基本状态估计模型

对于每个时刻t，状态估计的任务是从含有噪声的系统向量Zt得到系统状态向量xt。具体而言，系统测量值满足模型[10]，即

Zt=f(xt)+ξt

(1)

式(1)中：Zt为n维实时量测向量；xt为m维状态向量；f(·)为量测函数；ξt为量测噪声，其中还包括建模误差。状态估计的首要问题是对f(·)进行建模。

传统电力系统状态估计算法通常先进行物理建模，然后将原始量测量数据带入潮流计算，获得电力系统当前的最优估计值。此时式(1)中的Zt包括支路功率量测、节点注入功率量测、节点电压幅值量测，xt包括节点电压幅值和相角。WLS状态估计法以残差的加权平方和的最小值作为约束条件，且受初始值和异常值扰动影响大，在求解过程中存在时效性差、精确性差、复杂度高等问题。

2 算法模型原理

2.1 神经网络DNN

DNN由输入层、输出层以及多个隐含层全连接构成，其数学原理包括前向传播和反向传播，两部分交替进行。前向传播阶段：隐含层将前一层的输出作为后一层的输入；反向传播阶段：通过随机梯度下降把结果迭代优化，使得损失函数取到极小值，从而求得网络的最佳参数，包括线性传递系数ω和偏置常数d。损失函数通常根据目标进行选择，采用对异常值敏感，且具有很好鲁棒性的均方根误差(root mean square error, RMSE)作为目标函数进行优化[11]，表达式为

(2)

(3)

η为步长，一般取大于0的值；Ai(i∈[0，N])为由量测向量生成的 内部输入；Sη(x)为软阈值算子，也称激活函数，一般采用ReLU函 数，可以匹配相关特征和更好地实现数据拟合，具体形式见式(4)； 对第i次外循环中的第k次内循环而言，为此时的线性传播系数图1 DNN网络的结构Fig.1 Structure of DNN network

其余参数设置规则如下。

(4)

(5)

(6)

式中：μi和Bi分别为第i次外循环的控制系数和伪量测；I为外部循环的总次数；i和k的取值范围分别为[0,I]和[1,3]。但是对于单一的DNN模型来说随着神经网络层数的增多，优化函数越来越容易陷入局部最优解的陷阱中，并且梯度消失现象更加严重。

2.2 近似线性网络

(7)

(8)

经过推导可以将式(7)化简为套索问题，解决此类问题可以用快速迭代收缩阈值算法(fast iterative shrinkage-thresholding algorithm，FISTA)[15]。逐次在正值区间内取k值进行递归计算，式(7)就可以转化为式(9)。

(9)

在上述图1所提的模型中，通过设置适当的参数μi和步长η解出收敛于式(8)的电压序列{Vi}。在实际应用中，图1所示的模型往往需要进行k次内迭代来逼近式(7)中的最优解。此外，每次外环迭代都需要计算伪量测Bi，这些都限制了它的大规模实时应用。通过输入参数与中间层的跳跃连接，设置超参数、激活函数，利用神经网络的前向计算和反向传播等方式来解决上述不足。

3 DNN-PN混合网络模型

神经网络拥有容错性低、可以并行处理海量数据、自适应性强等优点，保证了它可以高效地处理非凸函数，以得到满足最小正则化和松弛成本的取值[16]。将传统的电力系统状态估计与神经网络融合到一起，为大数据时代新型电力系统的发展做出有力支撑。分步骤建立深度神经网络DNN和近似线性网络PN的混合模型，首先构造电力系统状态估计的模型，然后根据确定性线性近端技术设计近似线性网络模型，最后结合深度神经网络技术构建DNN-PN混合网络模型。

3.1 电力系统状态估计模型的基本参数

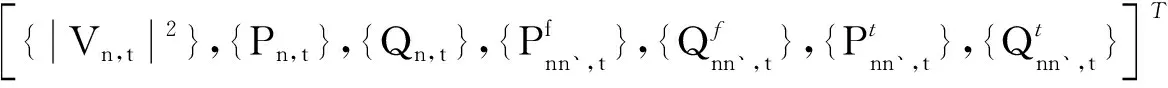
(10)

可以通过设置具体指示性参数来标记相应总线和线路的位置。

3.2 量测数据融合

现有的电力系统状态估计常根据SCADA系统数据，检索未知的系统状态。由于SCADA的采样周期一般为秒级，且不同量测点的量测装置一般不同步[17]。因此仅基于SCADA的监控数据已经不能满足当今新型电力系统对数据的要求。而电源管理单元(power management unit，PMU)的数据采样周期一般为毫秒级，可实现对信号采样的同步处理，但是由于成本和兼容性等问题PMU没有实现全域范围内的覆盖[18]。

进行量测数据的混合先是进行量测断面时间的对齐；其次，将刷新频率低的SCADA量测数据转换成与刷新频率高的PMU量测数据同步的伪量测；再次，通过赋予两者不同的权重来解决PMU和SCADA数据精度差异的问题；过程中将赋予高精度的PMU数据高权重，相对应地赋予SCADA数据低权重。最后通过量测变换的方法，建立融合量测系统。在现有数据的基础上，通过这种形式增加系统的冗余度，从而提高电力系统状态估计的精度。

3.3 粒子滤波

对比传统的高斯-牛顿法存在的对初值的依赖和梯度爆炸等问题，基于贝叶斯模型的粒子滤波状态估计是用样本均值代替求导运算，进而获得系统状态的最小方差估计，尽可能地实现最优估计[19]。针对电力系统条件不确定情况下的状态估计，可采用基于粒子滤波的序列重要性采样(sequential important sampling，SIS)的方法，并对之进行重采样。

重采样的思路是：在保持粒子数目不变的前提下，为了保障估计性能，舍弃权重小的粒子，用一些新的粒子来取代它们[20]。方法是将权重大的粒子进行复制，在权重大的粒子里面根据权重所占的比例进行分配。

(11)

(12)

将序列重要性采样的结果经过重采样，设置粒子的权重，得出的式(13)所示的状态后验分布更符合电力系统状态估计的实际需要。

(13)

3.4 DNN-PN的状态估计

为了充分利用神经网络和原始近似线性网络各自的优势，因此搭建的网络模型是一种将神经网络与传统物理模型相结合的混合算法模型。DNN-PN模型采用基于物理方程的迭代方式保证模型能进行海量数据训练和测试、加快处理速度、避免过拟合，弥补了以往仅仅用大量数值迭代计算来解决优化问题的不足。经过适当训练，模型中即使DNN网络隐藏层数很少，也能达到更好的效果。利用图2构建DNN-PN模型实现状态估计的具体流程。

图2 DNN-PN混合模型的结构Fig.2 Structure of DNN-PN hybrid model

是由真实值代入生成的外部输入，表达式为

(14)

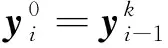
(15)

(1)直接将输入Z连接到中间层/输出层实现跳跃连接。

(2)每层具有的隐藏神经元是一致的。

通过比较分析，这些跳跃连接能够有效地训练DNN网络。此外这些跳跃连接也是隐藏层数固定的DNN网络具有近似线性能力的关键。

在DNN-PN混合网络中，需要调整的超参数包括I、k和y，同样也是近似线性网络PN模型所需要调整的参数。为了分辨不同的网络如何影响性能，默认使用ReLU为激活函数，以达到控制变量的目的。

图3是DNN-PN混合网络用于电力系统状态估计两种模式的运行流程图。离线训练阶段：利用SCADA和PMU的历史融合数据，分析系统注入复功率的概率分布；再通过贝叶斯估计中的粒子滤波算法，利用序列重要性重采样，生成注入复功率的样本数据集，进而产生离线训练阶段的DNN-PN混合网络的训练样本，训练深度学习网络。在线状态估计阶段：根据从离线训练阶段获得的网络结构参数建立网络；再将实时PMU数据通过在线的DNN-PN混合网络实现状态估计。由深度学习的数学原理进行分析，DNN-PN混合网络利用反向传播算法训练生成网络架构，然后使用训练好的DNN-PN混合网络通过前向传播计算实现电力系统状态估计。

图3 DNN-PN状态估计方法的结构Fig.3 Structure of DNN-PN state estimation method

4 算例分析

4.1 数据集设置

为验证本文方法的准确性和时效性，进行仿真验证，数据集由2012年的负荷数据来生成。将负荷数据标准化来匹配系统中的功率需求，MATLAB中的MATPOWER工具箱可以将标准化的负荷数据作为输入，代入交流功率方程中，求解出真实电压Vt，并得到测量值Zt。

电力系统状态估计中，涉及的量测量众多，数值和量纲也有较大的差异。为了减少上述因素对近似线性网络输出的影响，提高估计结果的精度，需要对网络的输入输出数据进行归一化处理。统一将所得数据集的80%作为训练集，剩下的20%作为测试集。

4.2 实验设置

所有的算法都是在Ubuntu18.04系统上进行训练的，处理器为Intel® CoreTMi5，内存为16 GB，显卡为NVIDIA GeFeorce MX350 2G。 在系统上搭建了基于Anaconda的Python的编译环境，同时安装了Pycharm作为编译软件进行调试，软件框架结构为基于Keras深度学习工具的Tensorflow-gpu框架。Cuda和Cudnn利用GPU的并行处理的算力优势可以加速深度学习的进程。

实验所用的神经网络用tensor进行训练，算法的权重由基于反向传播的优化算法Adam，配置参数设置如表1所示。

表1 Adam参数设置Table 1 Adam parameter settings

表1中， 学习速率或称为步长的设置通常需要多次调试，才能得到比较理想的结果；β1和β2分别为第一次和第二次估计的指数衰减率；容许误差值需要选取极小的常数，取值会影响迭代次数。并设置了丢弃法(dropout)和早停机制来防止过拟合。训练时每200个epoch为一个循环周期，epoch表示所有数据送入网络模型完成一次前向计算及反向传播的过程。为了减少因为训练算法引入权重所造成的随机性，所有的网络独立地训练和测试20次。在训练和测试阶段，设置近似线性网络的初始值为，k=3进行模拟。利用控制变量法，选择DNN-PN混合网络， 6层FNN算法，高斯-牛顿算法和LSTM算法具有相同的深度。所有神经网络中，每层隐藏单元的数量需要等于输入的维数，如此IEEE118节点系统的维数为118×2=236。

4.3 结果分析

实验使用IEEE118节点系统构成测试算法估计性能的测试系统，利用负荷数据进行仿真得到多维度潮流数据作为真实值，在多维度潮流数据中加入量测噪声来模拟实际量测值。这样共计生成了18 528个电压量(包括幅值、相角)，其中14 822个用于对模型进行离线训练，其余3 706个用以测试其性能。所得到的DNN-PN混合网络与其他算法的估计结果对比如图4所示。

在节点500～550处，数据截面50和数据截面100的电压真实值以及由DNN-PN混合网络、高斯-牛顿法、6层FNN和LSTM获得的估计值见图4(a)和图4(b)。在同一节点时DNN-PN混合网络相对于高斯-牛顿法，对状态估计模型精度和鲁棒性都有所提升，且在电压幅值方面提升比较明显。对图4(c)和图4(d)进行分析可知，在数据截面500上，节点1～节点50处DNN-PN混合网络的估计值相对于高斯-牛顿法的估计值提升比在数据截面550上节点50～100处的大，这是由于随着训练的进行，高斯-牛顿法也能比较好地拟合真实值；但是随着规模的扩大，DNN-PN混合网络在时间成本上的优势会越明显。故将从误差分析和时间成本分析两方面进行定量分析，进一步说明了DNN-PN混合网络的优越性。

图4 IEEE118节点系统状态估计结果对比Fig.4 Comparison of status estimation results of IEEE118 bus system

4.3.1 误差分析

对于t时刻，开发的PSSE方案接收测量向量Zt的状态向量Vt∈R2N。然而，当Zt中存在数据缺失时，其性能就很受影响，这在SCADA和PMU融合的数据系统中很常见，比如出现仪表或通信故障等问题。为了模拟这其中的一些情况，本实验所有节点的测量值Zt都添加高斯白噪声，其中设定功率和电压的标准偏差分别为0.02和0.01。DNN-PN混合网络、高斯-牛顿法、6层FNN和LSTM等几种算法经过3 706个测试数据的测试，其50次测试平均后电压幅值和相角的平均绝对误差(mean absolute error, MAE)和均方根误差(RMSE)如表2所示。

表2 IEEE118节点系统状态估计结果Table 2 IEEE118 bus system state estimation result

在预设条件下由表2易知，DNN-PN混合网络在于其他算法的比较时，均呈现出很好的性能。在该测试系统增加高斯白噪声的情况下，本文方法在电压幅值和电压相角上的估计误差较高斯-牛顿法分别降低了17.4倍和9.1倍。高斯-牛顿法应用的最小二乘法先要设置初始值，而初始值的设置影响迭代的次数，在其进行多次迭代以后，常常不能收敛到真实电压值，还会由于目标函数的非凸性，往往存在多个最优解。在添加高斯白噪声的测试系统进行的仿真实验中，本文方法依然精度较高，证明了在实际系统中其具有很好的鲁棒性。

4.3.2 时间成本分析

表3给出了不同状态估计算法进行50次状态估计的平均估计时间和训练时间。

表3 各种算法状态估计的测试时间Table 3 Test time of state estimation of algorithms

由表3可以很明显地看出，传统的高斯-牛顿法很难满足目前状态估计在线应用的实时性要求；而所提出的DNN-PN混合网络模型的状态估计方法利用神经网路的前向传播和反向传播计算代替了传统的迭代计算，基于GPU的并行计算取代了串行计算，所需要的时间很短，估计效率在此种规模的电力系统中具有很大优势。在仿真测试中，本文方法的计算效率和训练效率相比于高斯-牛顿法分别提升了55.7倍和36.5倍，随着系统规模的增大，优势越来越明显。LSTM算法由于存在输入门、遗忘门和输出门，使得计算参数变多，这些导致其计算速度较慢。

5 结语

提出了一种基于DNN-PN混合网络模型的电力系统状态估计方法。通过理论推导与仿真分析，可以得出下结论。

(1)DNN的结构里引入PN使得下层神经元与上层神经元建立起直接的通信，保证能充分利用数据，不陷入局部最优解的问题；激活函数ReLU的运用使得梯度消失得到了解决，且对非线性问题有很好的性能。

(2)整个电力系统状态估计分为离线训练阶段和在线状态估计阶段，在线阶段将融合数据进行预处理之后，将数据送入离线阶段训练好的神经网络结构和权重建立的网络，利用神经网络可以高效地处理非凸函数，获得最小正则化和松弛成本的取值。

(3)相较于传统的高斯-牛顿法，DNN-PN混合网络在降低电压幅值与电压相角估计的均方根误差和减少时间成本等方面有了很大的进步；相对于其他的神经网络算法，计算的准确性和鲁棒性等方面也有一定的竞争力，有望在真实场景下进行应用。