钻井岩屑回注作业中裂缝扩展规律

李斌， 严海源， 严卫杰， 雷克， 石成辉， 张贵磊， 张帅， 冯永存*

(1.中海油田服务股份有限公司， 廊坊 065201； 2.中国石油大学(北京)石油工程学院， 北京 102249)

随着页岩气以及海洋油气的大力开发，油基岩屑等固相污染物的产量急速上升，给油田现场污染物处理带来巨大挑战[1]。此外，在面对日益严苛的环保要求下，传统处理方法效率低、成本高的问题日益突出。而岩屑地下回注封存技术(以下称为岩屑回注技术)已经被证实是高效、低成本处理油基岩屑的重要手段。

岩屑回注技术是将岩屑充分研磨后与海水或油田废水充分混合，通过添加化学药剂使其成为稳定的浆体，然后利用高压泵组以水力压裂的方式注入目标地层，实现油基岩屑等污染物的永久封存。岩屑回注技术与水力压裂技术的明显区别在于岩屑回注作业需要间歇施工，所产生的诱导裂缝与水力压裂裂缝不尽相同。因此，若以水力压裂裂缝扩展规律描述岩屑回注裂缝扩展存在较大误差，导致岩屑回注施工设计失败，最终导致岩屑回注作业过程中裂缝穿透隔层沟通其他储层或地下含水层，造成不可逆的污染。因此，准确描述岩屑回注过程中裂缝的几何形态和延伸规律是岩屑回注作业设计的重要组成部分[2-3]。而裂缝扩展的三维几何形态(缝高、缝长、缝宽)的影响因素众多[4-5]，其中回注过程中主要以施工参数为主。因此，综合考虑在非线性流固耦合条件下，建立合适的回注裂缝扩展模型来预测上述过程，成为中外学者广泛研究的方向。

传统的水力压裂过程是基固体力学与流体力学复杂的非线性流固耦合过程。Nordgren[6]应用有限元数值求解方法建立流固耦合模型，研讨施工参数对于水力压裂裂缝扩展的影响；Victor等[7]基于流固耦合理论以及断裂力学理论，建立了水力压裂二维模型;2018年，Brice等[8]、Anthony等[9]基于常见的KGD模型与PKN模型分析了裂缝长度、簇间距、水平应力差、压裂次序对于裂缝几何形态分布影响。为了进一步描述裂缝扩展前缘附近的多尺度结构，Papanastasiou[10]考虑注入液在裂缝内流动和裂缝扩展的非线性耦合，建立了裂缝扩展计算模型，将有限差分法与有限元法相结合，模拟了该模型下的裂缝扩展形态。2019年，沈国军等[11]基于扩展有限元法(extended finite element method，XFEM)裂缝扩展分析方法和压裂液对油页岩裂缝扩展的影响模型,采用Abaqus数值模拟软件,对吉林省汪清地区的油页岩进行了不同黏度和不同排量压裂液条件下的裂缝扩展仿真模拟。李小龙[12]基于地层流-固耦合方程，建立XFEM模型，利用最大主应力准则、最大能量释放率准则判断裂缝起裂与扩展过程，量化分析了不同参数对裂缝形态的影响规律，并对影响因素进行了灰色关联分析，最后通过大型真三维物模实验在一定程度上验证了数模结果的正确性。2020年，高振南等[13]基于流体相态特征和储层应力敏感规律，开展流体渗流-多孔介质变形动态耦合研究及评价，研究在在不同回注制度下的裂缝扩展区域。李明辉等[14]基于全局黏聚区模型建立大斜度井3条裂缝同时扩展的有限元数值模拟，对不同井斜角、原位应力差条件下的裂缝注入点压力、裂缝形态进行研究。2021年，赵发寿等[15]基于稳定渗流理论,结合回注井储层物性和回注井动态数据,建立回注井渗流模型,研究回注井极限注入量、剩余可注入量、可回注年限对裂缝扩展前缘的影响。并通过常规容积法计算对比分析,最终进行计评估回注井极限回注量,掌握回注井极限回注量,避免因回注井回注能力问题造成停产的风险。2021年，Aziaov等[16]提出研究油滴和固体颗粒共注入的研究，用于预测乳液回注过程中渗透率降低的模型。讨论了影响裂缝扩展的物理参数以及液滴与孔壁之间的物理化学相互作用。这些研究推动了对于裂缝扩展的认识，但为了得到准确的结果，回注作业裂缝扩展模型必须正确地解决断裂前缘附近不同尺度下的有限水力裂缝的扩展问题[17-19]。又因为不同渐近区域的范围随着岩石和注入特性的变化而变化，因此在某些情况下需要非常精细的网格，从而导致数值计算变得很困难，现场实用性较差。

实际上，岩屑回注作业数值模拟是将液体从稳定点源以恒定速率间歇性注入地层的过程，需要考虑岩石弹性变形、回注液在裂缝间流动以及水力裂缝扩展的复杂过程。为了保证上述回注作业安全高效地运行，不发生海底泄漏或伤害地下水资源和油气资源等事故，因此，研究其裂缝扩展规律很有必要。

现提出一种基于开源程序PyFrac[20-22]实现岩屑回注过程中水力裂缝延伸的数值模拟方法，建立符合岩屑回注作业数值模型，实现岩屑回注裂缝扩展仿真模拟。该方法将稳定运动的水力裂缝的近尖端渐近解与裂缝的有限离散化耦合起来，通过求解近端水力压裂渐近解，避免近端多尺度结构数值求解，采用快速迭代法确定裂缝断裂前缘位置。因此，与其他断裂传播算法相比，创新性地采用更加精确单元中心有限体积方法离散化方程及求解，使求解过程更加迅速，且在网格密度较低的情况下保证较高的精度，即在相对粗糙的网格上也能获得高精度的数值解。

1 数学模型

岩屑回注作业中诱导裂缝数值模拟是经典的流固耦合问题，其中涉及岩石变形、裂缝间流体流动和裂缝扩展。通过PyFrac二次开发后的数值模型求解三维平面线弹性水力裂缝问题，以下简要说明数值模型中的控制方程、缝间流体流动类型、边界条件。

1.1 岩石弹性变形方程

对于纯张开型平面裂缝，将介质动量的准静态平衡简化为一个单一的超奇异边界积分方程，该方程涉及裂缝宽度ω和牵引矢量的法向分量。在均匀各向同性材料中，注入区域的平面断裂(随时间演化)进一步简化为

T(x,y,t)-σo(x,y)=

(1)

式(1)中：T为牵引力的法向分量， MPa;σo为远场原地压应力的法向分量，MPa;E′为材料平面应变模量，GPa；x′、y′分别为材料在牵引力矢量的法向分量作用下，随时间变化的坐标位置；ω为裂缝宽度，mm。

因此，式(1)解释了断裂张开度ω不是负值。更准确地说，在回注裂缝形成过程中，裂缝可能会闭合，因此会存在一个残余孔隙，该孔隙的张开度是压裂过程中裂缝的最大张开度与所在位置维持粗糙度所需裂缝宽度的最小值。进一步推导可得，当裂缝在指定位置打开时，裂缝面法向上的牵引力与流体压力相等。

(2)

式(2)中：ωa为裂缝张开的最小值，mm；ωr为维持粗糙度所需的裂缝宽度，mm；p为注入流体压力，MPa。

1.2 流体流动方程

回注作业裂缝内的流体流动可以近似看作润滑流，润滑流假设适用于裂缝扩展。基于流体质量守恒和动量守恒定律，计算裂缝的平均宽度，裂缝的质量守恒方程为

∂t(ρω)+∂Si(ρωVi)+2ρνL=ρQint(t)δ(x-xinj)

(3)

式(3)中：xinj为注入点坐标；Vi为裂缝平均宽度对应的流体速度，m/s；νL为流体从裂缝面泄漏到周围介质的速度(即裂缝壁处垂直于裂缝面的流体速度)，m/s；ρ为注入流体的密度，kg/m3；下角标Si表示在断裂面的方向。

守恒方程右侧的点源Qint模拟了回注浆液从井筒注入的情况，对于回注施工的实际井筒尺寸而言，随着裂缝尺寸的不断扩展，井筒的尺寸可以忽略不计。

由式(3)推导得，弱可压缩流体的裂缝平均宽度点处质量守恒方程可简化为

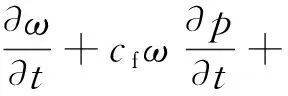
(4)

式(4)中：q为裂缝内的流体流量，m3/s;Q为流体注入速率，m3/s;cf为流体压缩系数。

因此，对于润滑流体的流动，裂缝平均宽度对应点处的动量平衡符合泊肃叶定律，是指通过细管稳定流动的流体速度随细管半径变化而变化，与细管的长度和黏度系数成反比，当流动过程中出现湍流时，流体流量q表达式为

(5)

(6)

式(6)中：flaninar=64/Re为层流流动时的范宁摩擦因数；Re为雷诺数；ReDeq为等效层流雷诺数；ωR为维持粗糙度所需的裂缝长度，mm；μ为流体的黏度，Pa·s;g为重力加速度常数，9.8 m/s2。

式(6)用于检测裂缝内部的层流向湍流转变的过程。对于这种二维或三维扩散方程具有与时间相关的边界条件，涉及耦合流体压力与水力压裂的问题，对建模提出了重大挑战。最常见的解决方案是利用卡特漏失方法，该方法有两个主要假设。第一个假设是水力裂缝的传播速度远远快于特征扩散速度；第二个假设是流体净压力远小于原始有效应力，即忽略此假设下的流体净压力。因此，使用卡特漏失模型评估流体漏失速度，表达式为

(7)

式(7)中：CL为卡特漏失系数，m/s0.5；t为流体渗流时间，s；t0为流体渗流的初始时间，s。

1.3 裂缝扩展准则

一般认为压裂流体前端和裂缝尖端存在一个未知长度的滞后带。基于PyFrac的基本假设，即原法向压应力σo足够大时，压裂流体前端与裂缝尖端重合。因此，裂缝前缘的裂缝宽度不为零时，垂直于流体前缘的流体通量分量也消失，即

(8)

式(8)中：C(t)为t时刻的裂缝前缘位置；n(xc,t)为其对应的法线方向，xc为笛卡尔坐标系下裂缝尖端的法向坐标。

数值计算模型假设岩石是理想线弹性体，不考虑岩石非线性弹性变形与塑性变形，采用线弹性断裂力学中的断裂韧性建立裂缝扩展准则。认为裂缝尖端的应力强度因子等于岩石的断裂韧性时，裂缝开始扩展。基于上述假设，裂缝的传播条件如下。

(9)

式(9)中：V(xc)为局部裂缝传播速度，m/s;KIc为岩石断裂韧性，MPa·m0.5；KI为岩石局部应力强度因子，MPa·m0.5。

1.4 数值模型建立

利用二次开发后PyFrac创建尺寸为40 m×20 m，网格数量为71×45的矩形主控制区域(图1)。沿x轴和y轴方向对断裂面进行有限离散化，网格单元被划分为注入通道单元和水力尖端单元。以靠近水力尖端单元为测量点，将有限离散化与水力尖端渐近解耦合对上述非线性控制方程进行数值求解。该模型结合了裂缝前缘附近稳定移动水力裂隙的近尖端渐近解，即通过识别水力压裂尖端单元与其内部的注入通道单元来实现尖端裂缝宽度的求解。更准确地说，是通过得到裂缝宽度增量与尖端压力的全新解法。该计算模型可更准确地得到回注作业中裂缝宽度与流体压力。

前文提及民宿运营模式发生了变化，亦可解释如下：第一阶段，民宿主将自家房间租给游客使用，是先有物质基础与场所氛围，继而产生相应的精神共鸣，人们向往这种共鸣的现象推动了第二阶段的民宿发展；第二阶段的民宿是目的性的发展其精神共鸣，再通过改造或新建来获得形式。根据现在民宿在旅游界大热的情况可以判定游客乐于接受被民宿主（或设计师）设定好的精神共鸣。

此模型中地层参数固定，分别为：岩石弹性模量为3.5×1010Pa、泊松比为0.4、岩石断裂韧性为5×105Pa·m0.5、平面应变模量为1.76×1011Pa、地层最小水平主应力为1.56 MPa、盖层最小水平主应力为7.56 MPa、漏失系数为10-5m/s0.5。在此基础上开展回注施工参数对裂缝扩展影响的数值模拟研究。主要研究不同施工排量、液体黏度和间歇时间对裂缝扩展的影响。

图1 数值计算模型示意图Fig.1 Schematic diagram of numerical simulation model

2 数值模拟结果与讨论

2.1 回注速度对裂缝宽度的影响

根据回注作业间歇注入的特点，模拟中设置回注液黏度为1.1 Pa·s、密度为2.4 g/cm3。模拟总时间为500 s，间歇时间为100 s，其中共有3个注入时段，分别为0～100 s、200～300 s和400～500 s。按照回注速度划分共进行了4组回注模拟，每组回注液注入速度分别为10-4、5×10-4、10-3、5×10-3m3/s。图2给出了在上述模拟过程裂缝宽度的变化；图3是裂缝最大宽度随注入速度的变化；图4是裂缝形状随注入速度和注入时间的变化，其中，以图4(a)注入时间499 s为参照标准，为不同回注液注入速度组设置了不同的回注时间，此处的时间设置需要考虑回注层性质等因素。

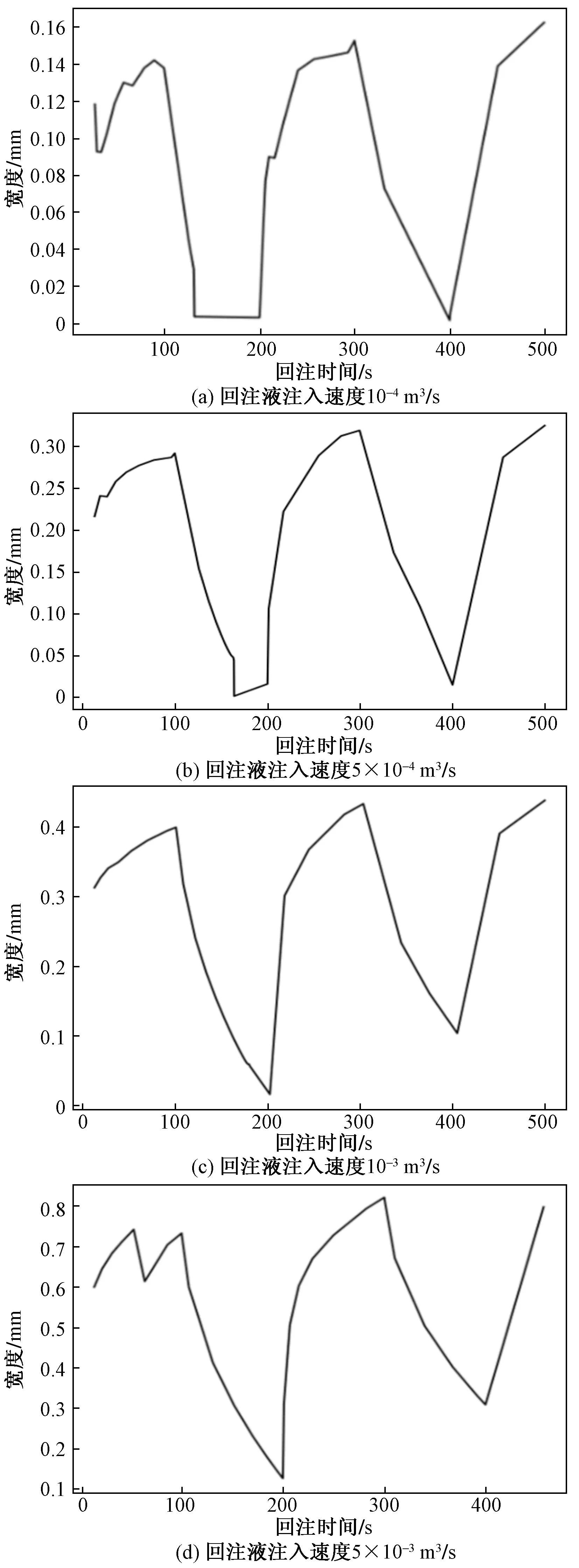
图2 裂缝宽度随注入速度和注入时间的变化Fig.2 Variation of crack width with injection rate and injection time

图3 裂缝最大宽度随注入速度和注入时间的变化Fig.3 The maximum width of the crack varies with the injection rate and injection time

图4 裂缝形状随注入速度和注入时间的变化Fig.4 Variation of crack geometry with injection rate and injection time

图5给出了在不同注入速度条件下，缝口压力的变化情况，反映了再次回注过程中液体克服地层应力，进一步打开裂缝的难易程度。

裂缝模拟结果表明，在总注入时间相同的情况下，裂缝宽度和长度与注入速度呈正相关。当回注速度由0.000 5 m3/s增大到0.005 m3/s时，裂缝宽度由0.32 mm增大到0.8 mm，裂缝半长由3 m增加到24 m。同时，裂缝扩展压力与随着注入速度增大而不断增大，而流体压力由于回注作业具有间歇性，在每两个注入段之间，存在一段压力降落期。但是如图5所示，在相同注入流速下，不同注入段中最大注入流体压力基本维持不变，变化幅度不超过±0.1 MPa。

上述模拟研究了同一施工方案下，注入速度恒定条件下的裂缝宽度与流体压力随注入速度和注入时间的变化。然而，实际回注施工在同一施工方案中常存在变排量注入情况。针对此特点，开展变注入速度条件下的裂缝扩展数值模拟研究。利用与前文相同的模型，保持其余地质条件不变，分别开展相同的注入总量条件下，注入速度递增(0.000 1、0.000 3、0.000 5 m3/s)和注入速度递减(0.000 1、0.000 3、0.000 5 m3/s)的裂缝扩展模拟。图6和图7分别给出了此条件下的裂缝宽度和流体压力变化情况。

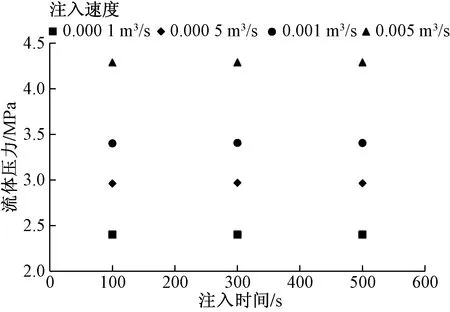
图5 缝口压力随注入速度和注入时间的变化Fig.5 Variation of fluid pressure at the fracture mouth with injection rate and injection time

图6 变注入速度条件下的裂缝宽度变化Fig.6 Change of crack width under the condition of variable injection rates

图7 变注入速度条件下裂缝压力的变化Fig.7 Fluid pressure change under the condition of variable injection rate

结果表明，在裂缝打开初期，裂缝的瞬时宽度与注入速度呈正相关关系，因此初始裂缝宽度差异明显。在整个模拟过程中，递增与递减注入条件的裂缝宽度与流体压力交叉上升。但是，对全注入时段的裂缝打开程度计算分析发现，在总注入量相同的情况下，回注速率对裂缝宽度和裂缝压力的影响很小。

2.2 回注液黏度对裂缝宽度的影响

岩屑回注作业中，回注液黏度是衡量注入液的重要指标，也是影响裂缝扩展的重要参数。回注液黏度变化影响裂缝内压力梯度，进而影响地层岩石变形，对最终裂缝扩展形态产生显著影响。采用上述模型，在地层参数不变、注入总时间为500 s、间隔时间为100 s、注入速度为0.001 m3/s条件下，分别进行4组黏度(0.003、0.004、0.005、0.006 Pa·s)下的数值模拟。图8和图9分别为缝口宽度和缝口压力随回注液黏度变化图。

图8 注入时间500 s时缝口宽度随流体黏度的变化Fig.8 The fluid pressure changes with the viscosity of the reinjection fluid at 500 s

图9 注入时间500 s时缝口压力随流体黏度的变化Fig.9 The fluid pressure changes with the viscosity of the reinjection fluid at 500 s

2.3 回注间隔时间对于裂缝宽度的影响

在岩屑回注作业中，回注作业的间隔时间也是影响裂缝扩展的重要因素，在回注间歇期裂缝内流体滤失到地层中，裂缝内压力降低，地应力恢复平衡。采用上述模型，地层参数不变，液体黏度为0.003 Pa·s，注入速度为0.001 m3/s，每段注入时间为100 s，在回注总量相同的基础上,进行回注间隔分别为50、100、200 s的裂缝扩展模拟。图10为不同时间间隔裂缝宽度变化；图11是不同时间间隔裂缝形状图，其中，图11中显示的时间是在调整回注间歇时间后，整个回注模拟的总时间，分别对应间歇时间50、100、200 s，如图11(a)399 s表示100 s(注)+50 s(歇)+100 s(注)+50 s(歇)+100 s(注)=400 s，其余组时间同上。

图10 不同时间间隔注入条件下裂缝宽度变化Fig.10 Variation of crack width with different time intervals of fluid injection

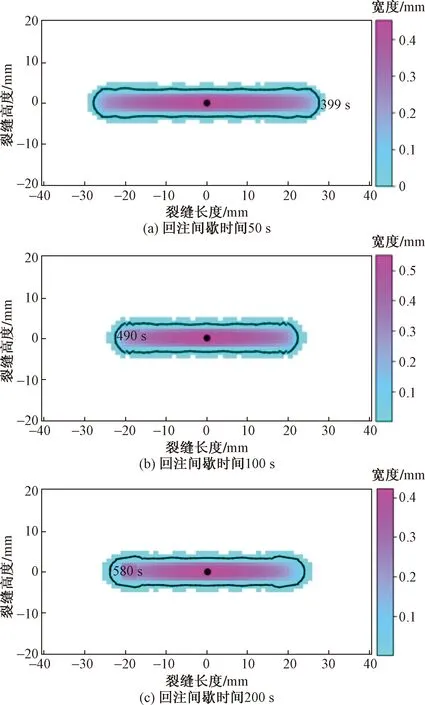
图11 不同时间间隔裂缝长度模拟图Fig.11 Variation of crack geometry with different time intervals of fluid injection

通过上述模拟结果发现，间歇回注为裂缝内部流体提供了滤失时间，降低了裂缝内部压力，间歇时间越长，裂缝内液体滤失越彻底，压力下降幅度越大。回注间歇时间50 s与回注间隔时间200 s相比，裂缝最大宽度几乎一致。在总注入量相同的情况下，时间间隔越大，裂缝闭合情况越明显，但是裂缝扩展的最大宽度几乎不变。相较于无间隔时间的压裂注入而言，一定的时间间隔允许携带岩屑的高黏度回注液能够在地层中充分展布，说明了间歇回注适合岩屑回注作业。

此外，实际岩屑回注施工过程中，间歇时间并不完全相同。因此，进一步模拟同一施工过程中不同间歇时间下的裂缝扩展。设计了两组对照实验模拟，基准参考是100 s间歇时间，以50、100、150 s三段逐步增大间歇时间的方式进行模拟，在保持总回注量一致的方式进行回注作业。图12为不同回注时间间隔下裂缝宽度的变化。

图12 不同回注时间间隔下裂缝宽度的变化Fig.12 Variation of fracture width under different reinjection time intervals

通过裂缝模拟结果表明，在保持回注总量一致的条件下，通过逐步增大回注时间间隔，发现裂缝扩展的最大宽度几乎没有发生变化，裂缝扩展的最大宽度因为回注间歇时间不同而错峰出现。但是由于回注时间间隔的不同，在间歇回注压力恢复期的裂缝最小宽度差异明显，回注间歇时间越大，裂缝闭合宽度越小。

2.4 实验验证

为了验证该裂缝扩展模型的准确性，进行了岩屑回注室内模拟实验，制作并使用全直径岩心，以水力压裂的方式间歇多次泵入交联悬浮液，实验结果与数值模拟结果进行对比分析。

实验1为定注入速度的回注模拟实验，实验方案与结果见表1。上述实验为使用10 mPa·s的低黏度悬浮液以定注入速度即可压出裂缝(图13)，可以看到裂缝周围发生滤失，说明岩心悬浮液滤失量较大，由图14悬浮液注入时程曲线可以看出，曲线有两个最高点，说明悬浮液造缝后，继续进行了第二次造缝，随后进入延伸阶段，延伸压力波动变化，形成的裂缝形态不平整，在第一次注入段最高缝口压力达到4.2 MPa，之后两次回注段的最大缝口压力基本维持不变，图15数值模拟结果与实验结果吻合度高，说明该实验条件下模型的可靠性。

图13 岩心裂缝破裂模式Fig.13 Fracture mode of core fracture injection

表1 实验地层参数及实验方案Table 1 Experimental formation parameters and experimental scheme

实验2是变注入速度的回注模拟实验，注入速度逐段增加，实验方案见表2。保持注入液性能不变，仅仅改变注入速度，实验结果如图16所示，发现岩心外表面形成一条明显的可见裂缝，裂缝从岩心顶部到底部完全贯穿。岩心仅形成一条裂缝，裂缝形态较规整，破裂模式主要为拉伸型破坏。悬浮液滤失范围较大，裂缝滤失范围呈漏斗状。因此增大线性胶悬浮液黏度可以使裂缝形态更规整，易形成有利于充填支撑剂的有效裂缝。随着注入速度的增大，每个注入段的缝口压力随之增大，由图17实验悬浮液注入时程图与图18数值模拟中流体压力随着回注时间的变化对比分析发现，缝口压力增长趋势是一致的，也符合所讨论的注入速度与缝口压力的关系，说明了该数值模拟是具备实际参考意义的。

图14 实验悬浮液注入时程图Fig.14 Time course diagram of experimental suspension

图15 数值模拟中流体压力随着回注时间的变化Fig.15 The change of fluid pressure with reinjection time in the numerical simulation

图16 岩心裂缝破裂模式Fig.16 Fracture mode of core cracks

图17 实验悬浮液注入时程图Fig.17 Time course diagram of experimental suspension injection

图18 数值模拟中流体压力随着回注时间的变化Fig.18 The change of fluid pressure with reinjection time in the numerical simulation

表2 实验地层参数及实验方案Table 2 Experimental formation parameters and experimental scheme

3 结论

基于开源PyFrac进行二次开发，建立岩屑回注数值模型，对岩屑间歇注入过程中施工参数对裂缝的影响进行了研究，得到如下结论。

(1)注入参数对裂缝宽度和长度的影响分为两方面，注入速度对裂缝起裂宽度和长度变化有明显影响，注入速度越大，裂缝宽度越大，裂缝长度越长。在回注作业中，在合适的地层条件与地面管线和注入设备配合下,较大的注入速度有助于裂缝扩展延伸。在总回注量相同的情况下，回注液注入速度对岩石变形的影响很小，裂缝扩展宽度、裂缝扩展压力与注入速度之间关系不大，但对最终裂缝宽度影响明显，注入速度越小，最终裂缝长度越小，有利于在同一地层内注入更多浆液。

(2)注入液黏度对裂缝扩展形态有显著影响。增大回注液黏度，裂缝宽度与裂缝扩展压力也随之增大，此时裂缝长度变短，裂缝宽度变宽，相对较大的注入液黏度有利于限制裂缝扩展范围。

(3)间歇回注是岩屑回注作业的一个显著特点。一定的回注时间间隔可以帮助高黏度的回注液在地层中展布；但在回注量相同的情况下，间隔时间越长，裂缝宽度越小，裂缝扩展的最大宽度几乎不变；相比于无间歇回注，间歇回注裂缝宽度变短，裂缝扩展压力降低，保证了安全高效的回注作业，证明间歇回注适合岩屑回注作业施工。

(4)通过回注模拟实验与数值仿真研究对比分析，实验结果与数值模拟吻合度较高，证明了回注数值模型具备现实指导意义。

(5)上述结论展示了岩屑回注作业中裂缝扩展与回注施工参数的关系，但是对于地层参数等其他参数对裂缝的影响，还有待进一步研究。