多工况下兆瓦级海上风电齿轮箱均载性能优化设计

陈岩松，朱才朝，谭建军，宋朝省，宋海蓝

(重庆大学 机械传动国家重点实验室，重庆 400044)

为了应对日益严重的世界能源危机，风能作为一种最具发展潜力的绿色可再生能源，引起了世界各国广泛关注。风电齿轮箱是支撑风电机组高效开发风能资源的关键传动部件，但在时变风速作用下，百米级大尺寸、大柔性叶片与塔筒的耦合变形会使风电齿轮箱的输入载荷产生明显的随机特性，容易恶化齿轮箱行星级均载性能[1-2]，增大故障失效率[3]，因此开展多工况下风电齿轮箱行星级均载性能优化研究对提高风电机组运行安全具有重要的意义。

1 风电齿轮箱系统动力学建模

1.1 风电齿轮箱结构及传动原理

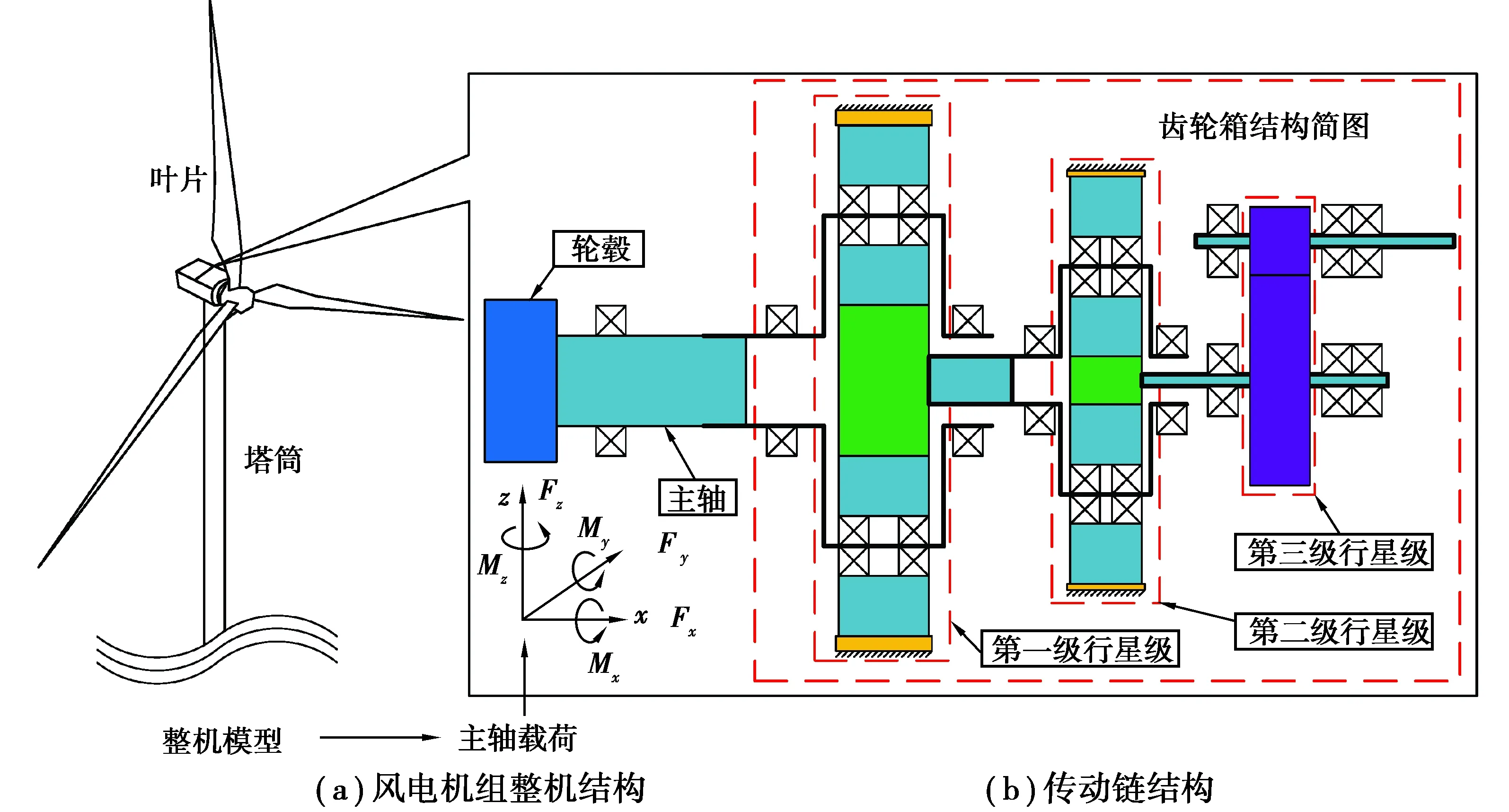
图1 风电机组结构图Fig. 1 Structure of wind turbine

表1 风电齿轮箱传动结构参数

1.2 风电齿轮箱系统动力学模型

1.2.1 外部激励

风速频率表示在风电机组20年运行期间内，相同平均风速总时长与测量时长的百分比值，是反映风场平均风速统计特性的重要参数。根据某风场风速统计数据[15]，采用双参数威布尔分布对风速频率进行拟合，其概率密度函数为

(1)

式中，k=8.426，c=1.708。

对应的分布函数为

(2)

式中：u为风速；k为形状参数；c为尺度参数。

考虑风切变效应，轮毂高度处的风速

(3)

式中：zhub为轮毂处高度；uhub为轮毂处风速；z为欲求的风速离地面高度。

采用Kaimal模型计算湍流风，湍流风在空间3个分量的谱为

(4)

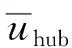
(5)

式中，Λu为湍流尺度系数。

空间中k,h2点处风速相关模型表示为

(6)

式中：PCoh(f)为空间相干度；Sk,k(f)和Sh,h(f)分别为k和h处的功率谱；Sk,h(f)为空间k和h处的互功率谱；f为频率。

1.2.2 内部激励

齿轮啮合是齿轮箱内部激励的主要来源之一。如图2所示，笔者采用齿轮分片法，将齿轮沿齿宽方向划分为若干薄片，用弹簧单元表示一对薄片齿的啮合，其啮合刚度通过ISO 6336标准[17]计算。齿轮副法向啮合刚度函数为抛物线模型，最大值在节点处，计算公式为

图2 轮齿分片示意图Fig. 2 Schematic diagram of gear slicing

cmax=c′CR，

(7)

式中：c′为单齿啮合刚度；CR为轮齿结构系数。

单齿啮合刚度的计算公式为

c′=cthCMCBcosβ，

(8)

式中：cth为理论单齿啮合刚度；CM为理论修正系数；CB为基本齿条系数；β为螺旋角。

理论单齿啮合刚度cth定义为

(9)

(10)

式中：zn1和zn2分别为主动轮和从动轮的当量齿数；x1和x2分别为主动轮和从动轮的变位系数。

齿轮时变啮合刚度函数可以表示为

(11)

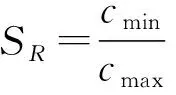
传动误差计算公式为

(12)

式中：φ10和φ20分别为主动轮和从动轮进入啮合时刻的初始转角；φ1和φ2分别为主动轮和从动轮转动的位移角；N1和N2分别为主动轮和从动轮的齿数。

1.2.3 齿轮箱系统动力学模型

采用SIMPACK建立风电齿轮箱系统动力学模型如图3所示。采用模态缩减法计算部件柔性变形[18-19]，其中，柔性体节点平移速度为

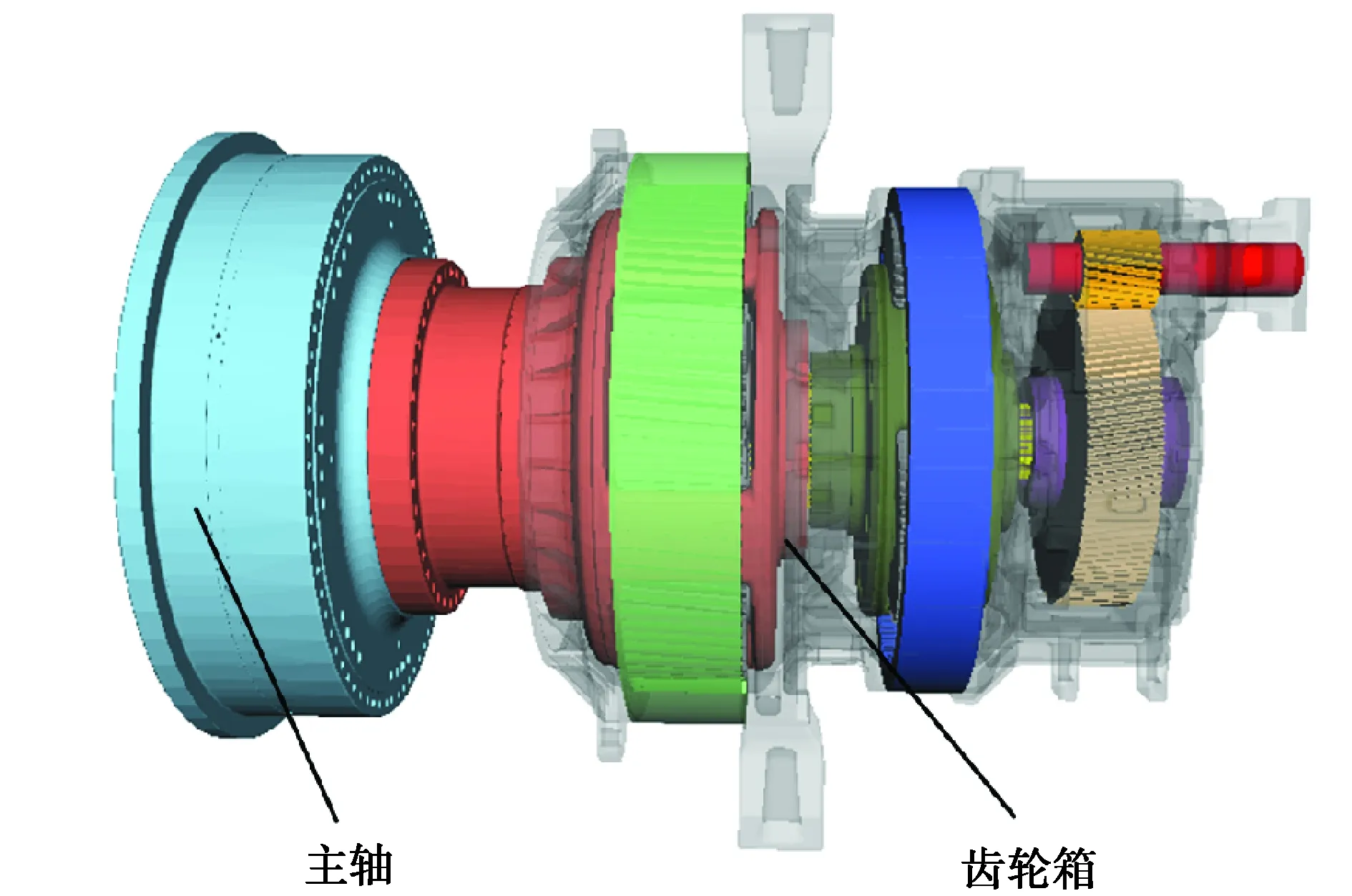
图3 SIMPACK齿轮箱系统动力学模型Fig. 3 Gearbox dynamic model of SIMPACK

(13)

式中：r为柔性体节点位移；GAB为局部参考到惯性参考的转换矩阵；s和u分别为柔性体变形前和变形后的节点位移；I为节点惯性张量；Φ为节点模态矩阵；ξ为节点广义坐标矩阵。

柔性体节点角速度为

GωJ=GωB+GωP，

(14)

式中：GωB为物体的角速度；GωP为由于物体变形引起的角速度。

基于公式(13)和式(14)，可得柔性体动能表达式为

(15)

式中，ρ,V,m和m分别为部件的密度、体积、节点质量和质量矩阵。

柔性体势能包括重力和弹性势能，其表达式为

(16)

式中：x为部件参考系相对于惯性参考系的位移；A为转换矩阵；g为重力加速度；q为模态坐标系；K为广义刚度矩阵。

基于式(15)和式(16)，可得风电机组齿轮箱系统动力学方程为

(17)

式中：D为模态阻尼矩阵；fg为广义重力；ψ为代数约束方程；λ为拉格朗日算子；Q为广义力。

2 风电齿轮箱均载优化

2.1 设计变量

齿轮修形一般包括齿廓修形和齿向修形。如图4(a)所示，针对齿廓修形，采用齿顶修缘，包括最大修形量e、修形长度λ和修形曲线3个要素。其中，修形曲线采用抛物线。如图4(b)所示，齿向修形则采用修鼓形方式。由于风电齿轮箱第一级行星级容易受到非扭载荷的作用，造成其动态性能较差[20]，因此重点优化第一级行星级齿轮修形参数，共计9个优化变量，如表2所示。

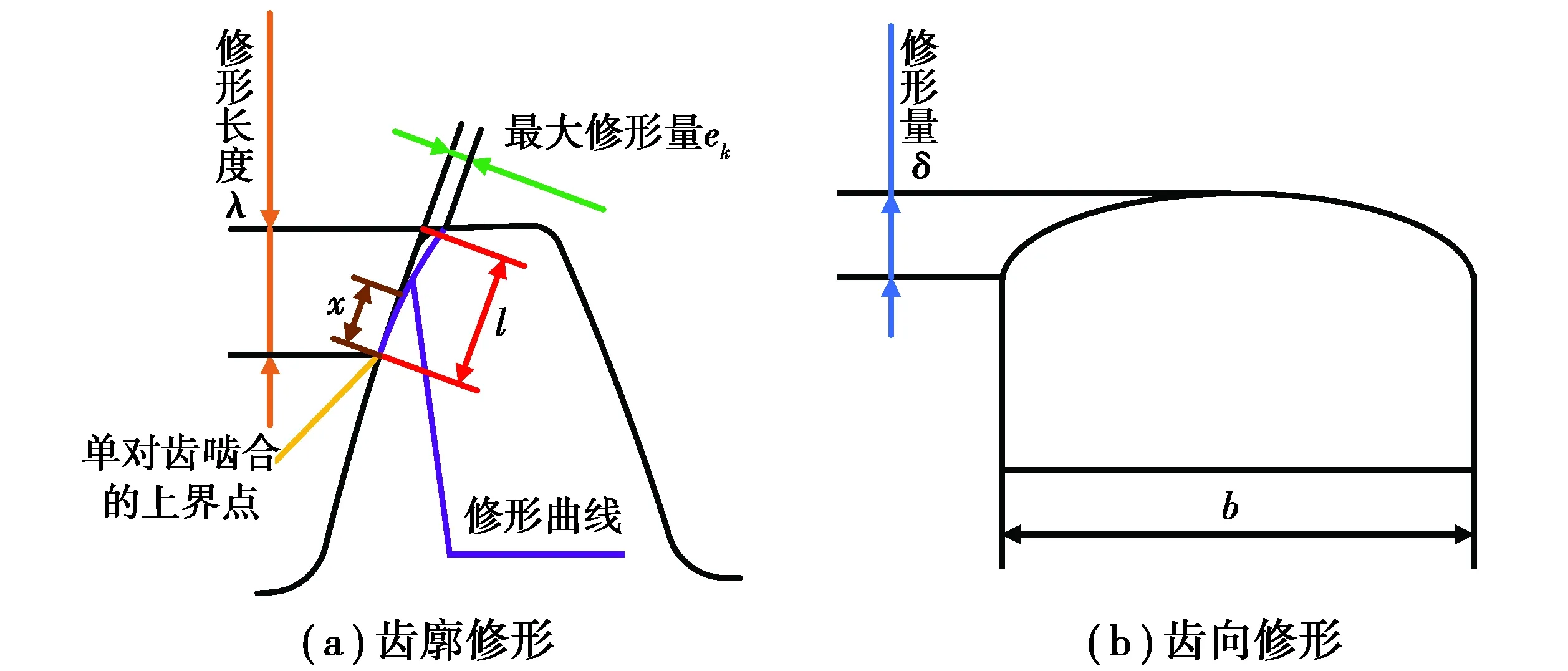
图4 齿轮修形示意图Fig. 4 Schematic diagram of gear modification

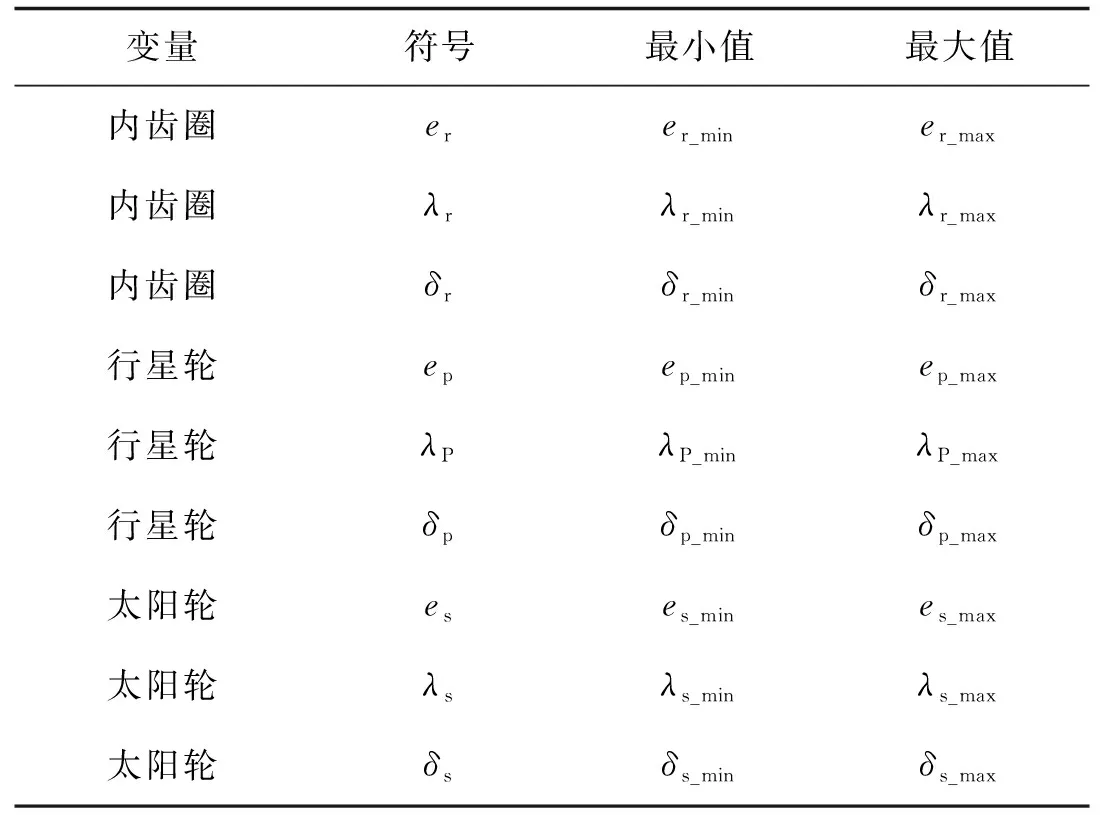
表2 优化变量参数表

2.2 约束条件

基于式(18)～式(19)计算齿廓修形参数[21]

(18)

式中：最大修形量ek=fKT+fm；fKT为弹性变形，加工误差fm=fpb+1/3ff，fpb为基节误差，ff为齿形误差。l为沿单对齿啮合的上界点至啮合始点长度。x为啮合位置坐标(原点在界点处)。

λ=Pb(εα-1)，

(19)

式中：λ为修形长度；Pb为齿轮基节；εα为齿轮端面重合度。

基于式(20)计算齿向修形参数[21]

(20)

式中：δ为鼓形量；Ft为啮合圆周力；b为齿宽。

分别选取式(18)～式(20)计算值的70%和130%作为表2中修形参数的最小值和最大值。

2.3 优化目标

如式(21)所示，对n种风速工况下行星级均载系数求和，并将其最小值作为优化目标。

minf∑=k1f1+k2f2+…+knfn，

(21)

式中，ki(i∈[1,n])为第i种工况对应的权重值，基于式(22)计算得到。fi(i∈[1,n])为第i种工况下行星级均载系数。

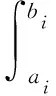
(22)

式中，f(u)为风速概率密度函数，可由公式(1)计算得到。ai和bi分别为该风速工况下的风速区间的下界和上界。

采用拉丁超立方抽样方法，对表2中9个优化变量进行抽样组合，然后将每一种抽样组合作为齿轮箱系统动力学模型(式(17))中第一级行星级齿轮修形参数的输入，并计算行星级均载系数[22-23]。最后，采用支持向量机回归(SVR)[24]重构第i种风速工况下齿轮修形参数与均载系数之间的映射函数，即可得式(21)中fi，其中fi(i∈[1,n])。

假设x是第i种风速工况下的9个齿轮修形参数，f(x)则是对应的均载系数，利用SVR可以构建x和f(x)之间的非线性关系为

f(x)=wTφ(x)+b，

(23)

式中：f(x)表示预测值；φ(x)表示非线性映射函数；w和b是系数[25]。

图5所示为在多风速工况下风电齿轮箱行星级均载特性优化流程。

图5 风电机组多工况优化流程Fig. 5 Flow chart of multi-operating condition optimization of wind turbine

首先，根据风速频率曲线(式(1))生成具有n种风速工况，并作为风电机组整机模型的外部激励，进而计算主轴与轮毂连接处六自由度载荷(Fx，Fy，Fz，Mx，My，Mz)；然后，将每一种风速工况下计算得到的主轴与轮毂连接处六自由度载荷作为齿轮箱系统动力学模型的载荷输入，计算不同齿轮修形参数组合(表2)下的行星级均载系数，并利用SVR构建修形参数与均载系数之间的映射关系；最后，将n种风速工况下行星级均载系数进行加权求和，以其最小值作为优化目标，采用遗传算法求解最优的齿轮修形参数。

在一台CPU主频为2.9G Hz的计算机上使用SVR进行齿轮修形参数寻优所需要的计算时间约10 min。而采用SIMPACK动力学模型进行一次计算需耗时20 min。由此可见，文中提出的优化方法可以大幅提高优化效率。

3 结果与讨论

3.1 外部激励分析

如图6(a)所示，从风电机组切入至切出风速区间5～23 m/s，间隔3 m/s，共计取n=7组风速工况，并利用式(22)计算对应的风速频率，作为式(21)中工况的权重值。参照IEC 61400-1标准，湍流强度设置为0.14[16]，可得额定风速(11 m/s)下u、v和w3个方向的湍流风速，如图6(b)所示。

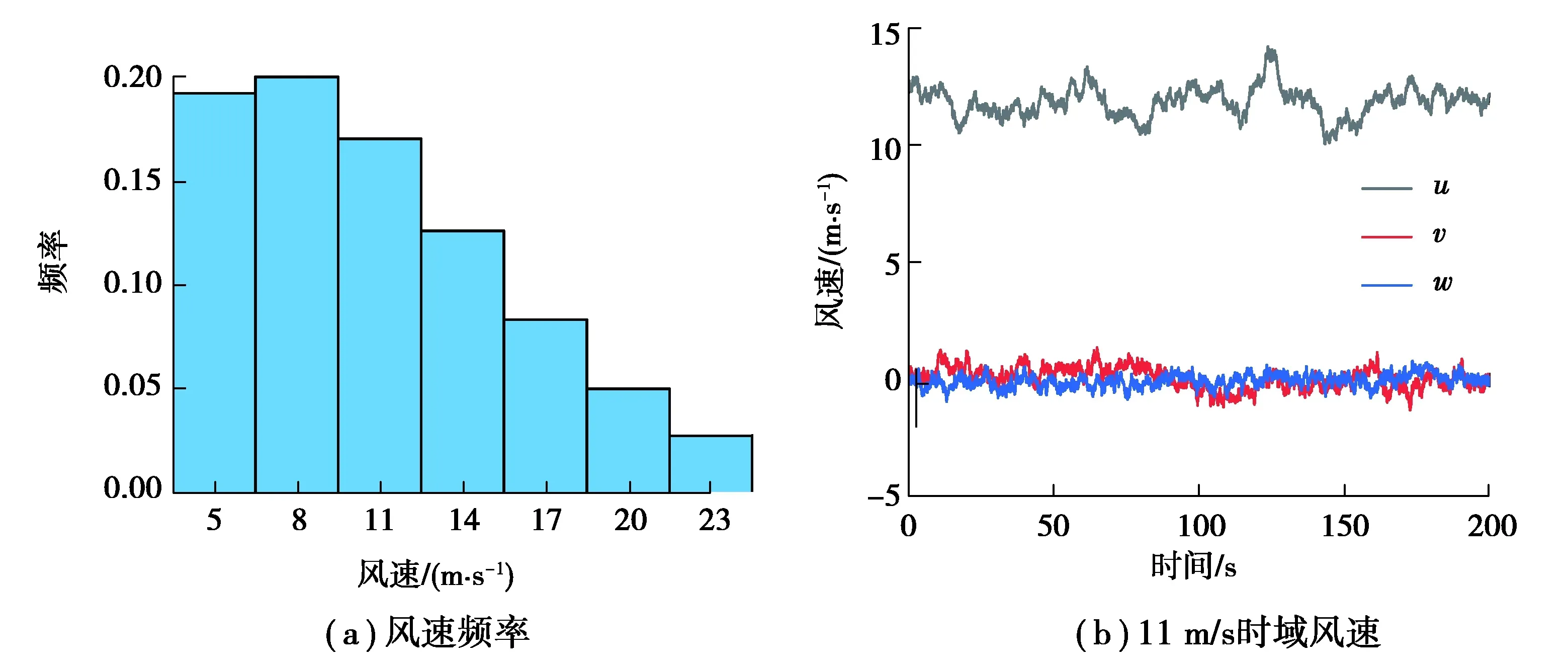
图6 风速频率及时域风速Fig. 6 Wind speed frequency and time domain wind speed

图7所示为7种风速工况下主轴与轮毂连接处的六自由度载荷。从图中可以看出，在额定风速以下，随着风速的增加，气动转矩也逐渐增大，但非扭载荷与气动转矩的比值显著下降；在额定风速以上时，由于变桨系统开始运行，此时主轴处气动转矩近似恒定，而非扭载荷与气动转矩的比值逐渐增大。

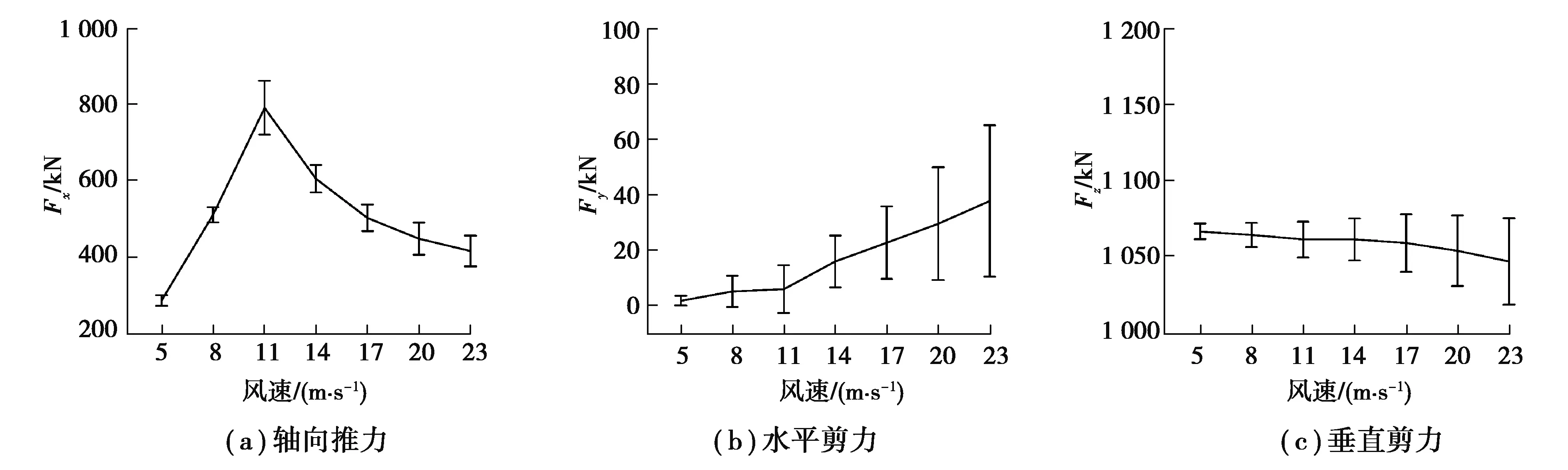
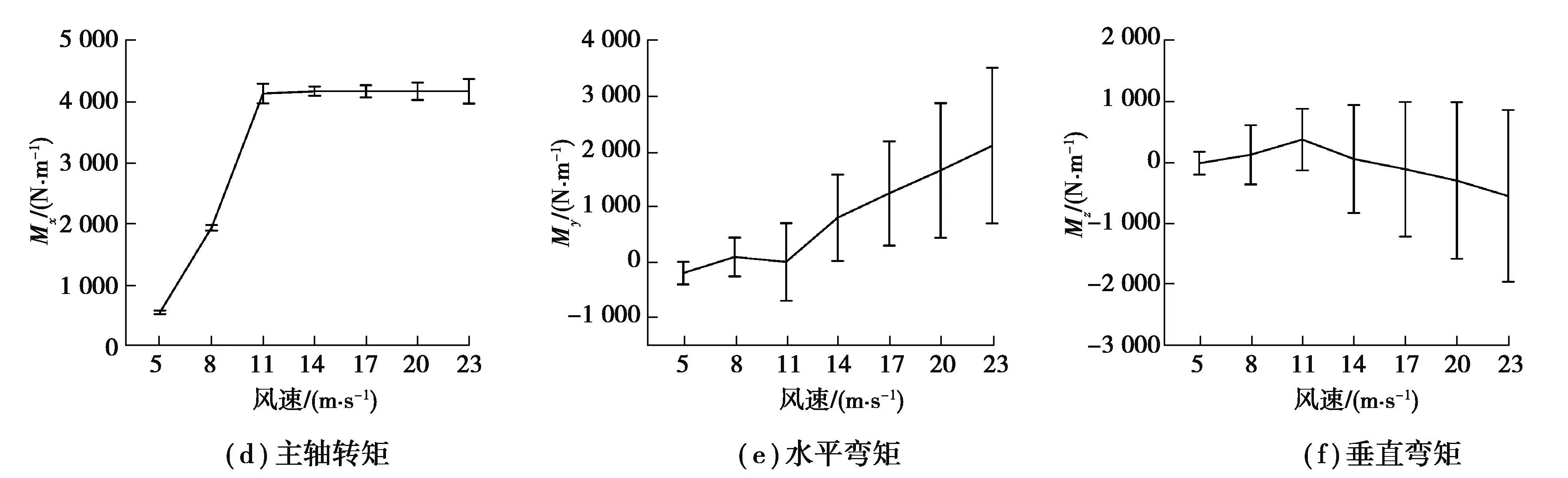
图7 不同风速下主轴载荷Fig. 7 Mainshaft load under different wind speeds

3.2 内部激励分析

笔者仅针对第一级行星级齿轮开展修形优化设计，图8所示为非扭载荷对齿轮箱行星级齿轮副传动误差的影响。从图中可以看出，随着风速的增加，传动误差幅值也逐渐增大；当考虑非扭载荷时，传动误差幅值略有增大。

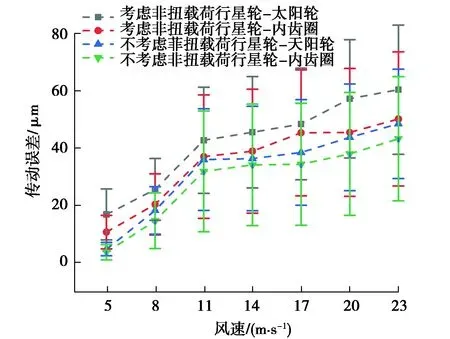
图8 非扭载荷对传动误差影响Fig. 8 Influence of non-torque load on transmission error

图9 不同风速下优化前后行星级传动误差Fig. 9 Planetary gear transmission error before and after optimization under different wind speeds

图10所示为额定风速工况下行星级齿轮副时变啮合刚度优化前后对比。从图中可以看出，优化后的齿轮副啮合刚度激励(波动)显著减小。图11所示为不同风速工况下行星级齿轮副啮合刚度激励优化前后对比。从图中可以看出，齿轮副啮合刚度激励受风速工况的影响不大，整体变化较为平缓。但优化后的行星级啮合刚度激励显著降低。

图10 行星级优化前后齿轮副时变啮合刚度对比Fig. 10 Comparison of time-varying meshing stiffness of planetary gears before and after optimization

图11 不同风速下行星级齿轮副啮合刚度激励Fig. 11 Meshing stiffness of planetary gears under different wind speeds

3.3 齿面载荷分析

图12 额定风速下优化前后齿面载荷分布Fig. 12 Load distribution of tooth surface before and after optimization under rated wind speed

3.4 均载性能分析

通过行星轮和内齿圈动态啮合力计算均载系数k1，同时利用行星轮轴承力计算均载系数k2[24-25]，分别如式(24)和式(25)所示。

(24)

(25)

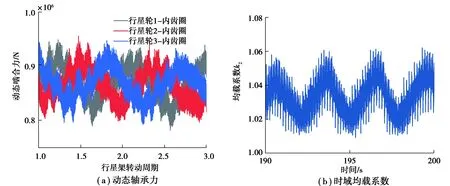
图13 额定风速下行星轮-内齿圈动态啮合力及均载系数k1Fig. 13 Dynamic meshing force and load sharing coefficient of planet-ring gear under rated wind speed

图14 额定风速下行星轮轴承力及均载系数k2Fig. 14 Dynamic bearing force and load sharing coefficient of planet gear under rated wind speed

利用式(26)计算行星轮上、下风向轴承力差值与轴承力额定值的百分比p。

(26)

式中：Fupwind和Fdownwind分别为行星轮上、下风向轴承力；Frated为额定的行星轮轴承力。

图15所示为第1个行星轮上、下风向轴承力差值。从图中可以看出，当不考虑非扭载荷时，行星轮1上、下风向轴承力差值较小，而考虑非扭载荷后，行星轮1上、下风向轴承力差值显著增大，但随着风速的增加，其差值又逐渐减小。其主要原因是在低风速工况时，气动转矩较小，行星轮轴承力也较小，此时行星轮轴承力易受到非扭载荷的影响[2,19]，而在额定风速及以上时，气动转矩为额定值，此时行星轮轴承以承担扭矩载荷为主。优化后的行星轮上、下风向轴承力差值明显减小，偏载现象得到明显改善，与图12结果相符。

图15 优化前后行星轮1上下风向轴承力Fig. 15 Upwind and downwind bearing force of planet gear 1 before and after optimization

图16所示为优化前后的行星级均载系数k1和k2对比。从图中可以看出，不考虑非扭载荷时，行星级均载系数随着风速的增加而增大，在达到额定风速后保持不变，但考虑非扭载荷后，随着风速的增大，行星级均载系数先减小再增大。结合图7可知，在额定风速工况以下时，随着风速的增加，气动转矩也逐渐增大，但非扭载荷与气动转矩的比值显著下降，因此行星级均载系数逐渐减小，均载性能提高。当达到额定风速后，主轴处气动转矩近似恒定，但非扭载荷与气动转矩的比值逐渐增大，导致行星级均载系数增大，均载性能降低。优化后的行星级均载性能在不同风速工况下均有所提升，在额定风速及以上时均载优化效果较好。

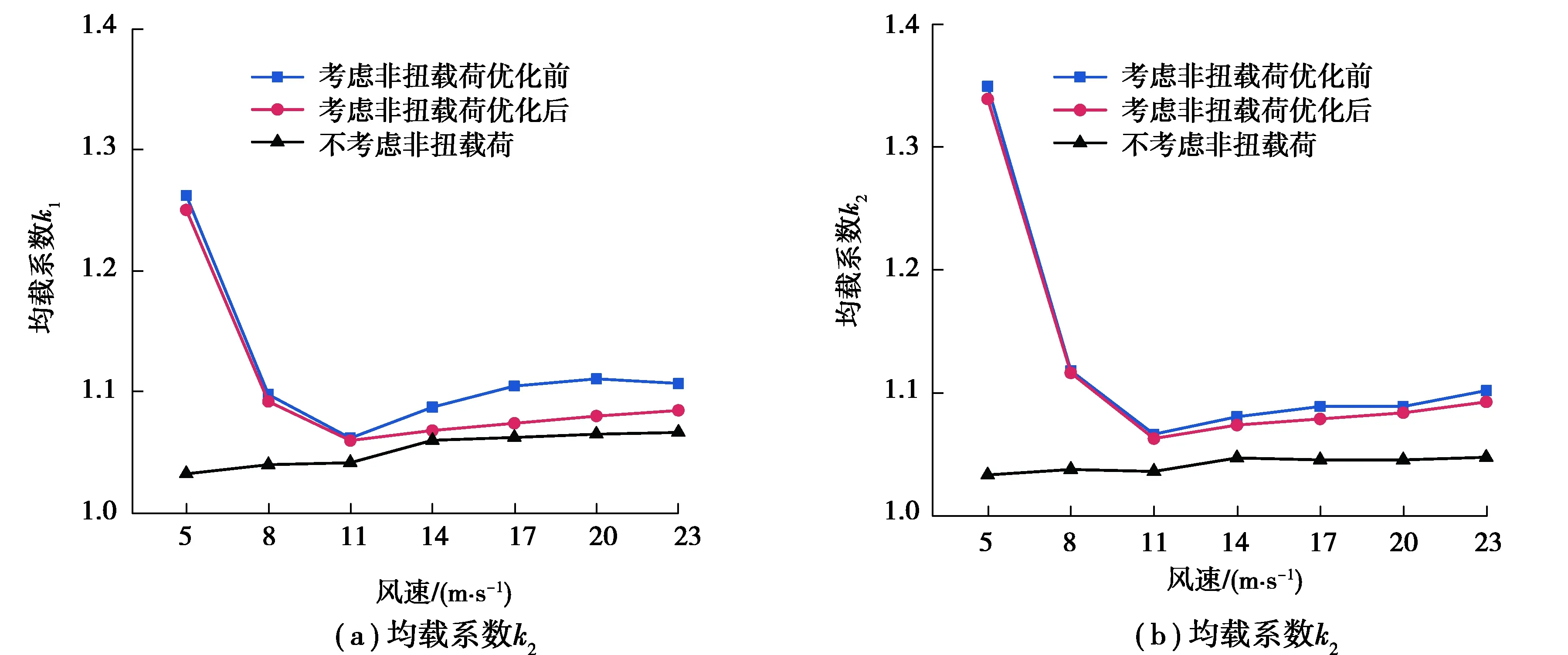
图16 优化前后行星级均载系数对比Fig. 16 Comparison of load sharing coefficient of planetary stage before and after optimization

4 结 论

该文考虑不同风速工况下风电齿轮箱时变输入载荷的影响，结合风电齿轮箱系统动力学模型，构建了多风速工况下风电齿轮箱行星级均载性能优化模型，以齿轮箱行星级均载系数综合最小为优化目标对行星级齿轮副进行修形优化设计，对比了不同风速工况下优化前后风电齿轮箱运行性能，得出以下结论：

1) 在额定风速以下时，随着风速的增加，非扭载荷与气动转矩比值显著减小，而在额定风速及以上时，在变桨控制作用下其比值逐渐增大。较大的非扭载荷占比会造成行星级齿轮和轴承产生明显的偏载。

2) 不同风速工况下，优化后的行星级齿轮副传动误差和啮合刚度波动幅值均显著降低，并且齿面载荷分布均匀，行星轮上、下风向轴承的偏载现象得到有效改善。

3) 随着风速的增加，非扭载荷占比变化会使行星级均载系数先减小再增大，并且优化后的行星级均载性能在不同风速工况下均有所提升，在额定风速及以上时均载优化效果较好。