时间分数阶的非饱和渗流数值分析及其应用*

朱帅润，李绍红，钟彩尹，吴礼舟

（1.重庆交通大学 山区桥梁及隧道工程国家重点实验室，重庆 400074；2.上海交通大学 土木工程系，上海 200240；3.西南交通大学 地质工程系，成都 610031）

引 言

非饱和渗流问题广泛存在于岩土工程、边坡工程以及地下水科学等领域[1-5].经典的Richards 方程[6]可以描述孔隙介质中的非饱和渗流过程.由于水力传导系数与土水特征曲线的非线性特征，Richards 方程的解析解通常是较难获得的[7-8]，因此，Richards 方程的数值求解得到了很大程度的发展[9-10].数值求解过程中，一般会对Richards 方程进行数值离散，通常采用的数值离散方法包括有限差分法[11-12]、有限元法[13]和有限体积法等[14].例如，吴梦喜[15]发展了求解Richards 方程具有更好数值稳定性的一般有限元算法.Liu 等[11]采用有限差分法数值离散了分层非饱和土中的渗流方程.Zambra 等[16]构造了在空间和时间上具有很高精确度的有限体积法，用于求解非线性Richards 方程.通过上述数值方法获得的线性方程组需要迭代求解，此时Picard 法是最为实用和简便的[17-19].

近年来，很多学者从扩散现象的角度出发研究地下水在非饱和土体中的输运过程，发现其并不满足经典的Fick 扩散定律，也就是反常扩散过程[20].反常非饱和渗流本质上也是一种非Markov 过程，数值计算时则需要考虑渗流过程中的时间相关性或空间相关性[21].最近，关于分数阶方程已有很多研究和进展.例如，Pachepsky 等[22]提出了广义的Richards 方程，相比于整数阶方程，时间分数阶Richards 方程可以有效地表明土壤水分运移现象中存在的记忆效应.Gerasimov 等[23]结合时间分数阶扩散方程更好地拟合了烧制黏土砖吸水和在水泥砂浆中入渗的实验数据.Gerolymatou 等[24]对实验得到的具有适当初始值和边界值的分数阶Richards 方程进行了数值求解，并将模型结果与硅土砖中的水分入渗实验数据进行了对比，得到了较好的拟合结果.王睿等[25-26]采用conformable、Caputo 导数推导了含水率格式的分数阶Richards 方程，并与文献[27]的实验数据进行了对比研究.上述研究大多是对含水率格式的Richards 方程求解并与砖块水分入渗实验数据对比，因此，结合土柱入渗实验，分析非饱和入渗过程中孔隙水压力随时间的变化规律，能够为相关的岩土、边坡工程提供有力支撑.

本文结合Caputo 导数得到了具有更广泛渗流意义的时间分数阶Richards 方程，采用有限差分法进行数值离散并迭代求解，以及对分数阶参数和土水特征曲线进行了敏感性分析.最后，结合土柱入渗实验数据，并与经典Richards 方程的数值结果对比，对提出的时间分数阶Richards 方程的拟合效果进行了验证.

1 时间分数阶Richards 方程的数值近似

Richards 方程可以被用于描述多孔介质中的非饱和渗流问题，其沿垂直方向z的一维压力水头（h）格式的Richards 方程可以表示为[28-29]

式中，h为压力水头；K(h)为相对于z方向的水力传导系数；C(h)为容水度，其定义为C(h)=∂θ/∂h.在考虑入渗过程中的时间相关性时，时间分数阶Richards 方程的表达如下：

式中，γ为关于时间导数的阶次.当γ=1时，式（2）即退化为标准形式下的Richards 方程（1）.首先，对式（2）的求解，我们采用有限差分法进行数值离散，做网格剖分，令η，Δz分别为时间和空间离散步长，关于模拟时间被分为M等分，关于z轴上的长度被分为N等分，即

对于式（2）的右侧分数阶导数项需采用Caputo 分数阶导数定义[21]：

Γ(·)为Gamma 函数.式（5）中出现的压力水头导数的积分可以直接用数值微分公式逼近，其推导如下：

式（6）可以进一步简化为

对式（2）的左侧进行有限差分离散，有

其中

联立式（7）、（8）可得式（2）的离散格式如下：

式中，k为迭代步数，A为对称的三对角矩阵，h和b均为列向量.对于Picard 法的迭代求解过程，首先需要在每次迭代时导出线性方程组（12），然后使用基本的求解方法（例如Gauss 消元法、共轭梯度法）求解线性方程组[30].求解线性方程组后，式（12）中的系数矩阵A需要使用新的解向量hm,k+1进行更新，进而再次求解新的线性方程组.最后，前后两次解向量的相对误差满足如下迭代容差时，迭代过程终止：

ε为迭代容差，本文中均设置为10-8[31].

此外，有许多数学模型可以描述上述非饱和土中的水力传导系数和含水率与压力水头之间的数学关系[32-35].其中，Gardner 提出了如下指数模型[32]：

式中，Ks为饱和水力传导系数；θs和 θr分别为饱和含水率和残余含水率；α为土性相关的模型拟合参数.用van Genuchten[33]和Mualem[34]（VGM）模型来描述水力传导系数和含水率是比较经典的：

式中，有效饱和度Se=1/[1+(|αh|)n]m；α，n和m均为与土性相关的模型拟合参数，m=1-1/n.

Fredlund-Xing（FX）模型描述的土水特征曲线如下[35]：

2 数值分析与应用

2.1 参数敏感性分析

基于上述时间分数阶Richards 方程的离散格式，使用MATLAB（版本：R2014a）开发了有关非饱和渗流的程序.为了验证分数阶阶次对非饱和渗流的影响，考虑三种土水特征曲线（SWCC）用于模拟在水平均质非饱和土中降雨入渗的一维瞬态流.数学模型如图1所示，土层的厚度假设为L=10 m，其中饱和的水力传导系数设置为Ks=6.0 × 10-2m/h[36].模型的边界条件如下：

图1 均质非饱和土的一维入渗模型Fig.1 The 1D infiltration model for homogeneous unsaturated soil

式中，h0代 表初始干燥土壤的压力水头值，并假设除去边界点的初始条件为h(z,t=0)=-10 m.

总模拟时间设置为2 h，空间步长 Δz=0.1 m，时间步长η=0.01 h，阶次γ 分别取为0.5，0.8，1.0，1.2 和1.5.我们在此示例中选择沙质土壤，采用了Lu 和Likos[37]的实验数据.使用三种数学模型对实验数据进行了拟合，如图2所示，可以看出三种模型拟合得到的SWCC 在趋势走向上基本一致，Gardner 模型在高基质吸力值处拟合不太好，VGM 和FX的确定系数R2分别为0.98 和0.99，在高基质吸力值处FX 模型拟合得更好.拟合参数包括土型相关的模型参数α，n，m，饱和含水率和残余含水率，如表1所示.

图2 SWCC的拟合曲线Fig.2 Fitting curves of the SWCC

表1 拟合参数Table 1 Fitting parameters

图3显示了t=2 h 时不同SWCC 形式下所计算的压力水头曲线，其中Gardner 和FX 模型的计算结果十分接近，在同一深度时两者均小于VGM 模型的计算值.在同一深度可以发现当γ＜1时，压力水头数值随着γ的减小有减小的趋势；当 γ＞1时，压力水头数值则随着 γ的增大有增大的趋势.此外，不同形式下阶次 γ对压力水头曲线的影响也存在明显差异，在Gardner 和FX 模型中压力水头值随着 γ的变化有较大的增幅（图3（a）、（b）），而在VGM 模型中压力水头值随着γ的变化增幅较小（图3（c））.这个结果表明了分数阶阶次γ 相对于1 越大，入渗速度越快，阶次γ 相对于1 越小，入渗速度越慢.

图3 不同模型和阶次γ 下获得的压力水头曲线： （a） Gardner 模型；（b） Fredlund-Xing 模型；（c） van Genuchten-Mualem 模型Fig.3 Pressure head curves obtained under different models and orders γ: （a） Gardner model; （b） Fredlund-Xing model; （c） van Genuchten-Mualem model

2.2 入渗实验与应用

入渗实验所用土壤为中国甘肃省天水市的次生黄土.土柱模型装置和实物如图4所示，降水模型箱为透明有机玻璃，有机玻璃柱高度为1.45 m，填土高度为1.25 m，外径20 cm，壁厚8 cm，距离土表面9 cm，14 cm，19 cm，24 cm，29 cm，39 cm，49 cm，59 cm，79 cm的侧壁分别开有9个小孔，用于埋设体积含水率和基质势传感器.在模型顶部距离设计填土高度顶部设计有一出水口，高度为2 cm，用于控制积水高度.供水装置主要由供水箱和滴水控制阀组成.供水箱材料为有机玻璃，分为内圆和外圆，高度均为10 cm，内圆外径20 cm，底部中心开有一个5 mm 圆孔，用于安装滴水控制阀，外圆外径30 cm，开有3 cm 排水管孔，试验中通过外环来调节内环水面，使供水箱水位始终保持同一高度，保证供水水压一致.滴水控制阀为医用输液管，可通过输液管控制阀调节恒定流量.

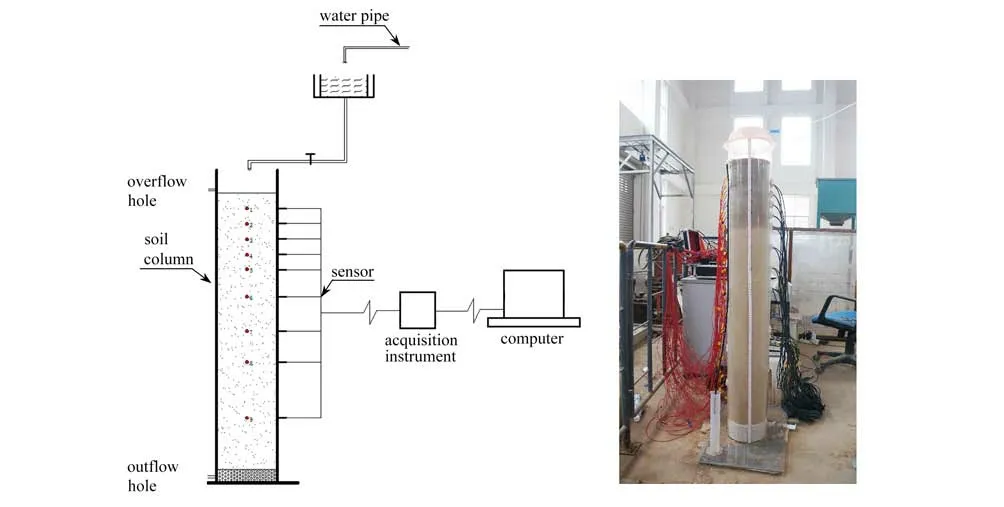
图4 土柱模型及供水装置Fig.4 The soil column model and the water supply device

水分测定装置由美国DECAGON 公司生产的EC-5 型体积含水率传感器（图5（a））、MPS-6 型基质势传感器（图5（b））以及EM50 数据采集仪（图5（c））构成.填土时将传感器探头埋入设计深度的土体内，并与数据采集仪进行连接，再通过USB 线连接到笔记本电脑，即可获得含水率和基质势数据.为了评价所提时间分数阶模型的拟合效果，选择了两个指标，即均方根误差（RSE）和相对误差（RE），分别表达为

图5 水分测定装置：（a） EC-5；（b） MPS-6；（c） EM50Fig.5 Moisture measuring devices: (a) EC-5; (b) MPS-6; (c) EM50

式中，hk为模型计算值，h*k为土柱实验中实测值，nn为测量的节点数.两个指标的值越小，表示模型的拟合效果越好.根据实验现场数据，模型的边界条件可以近似表达为式（22）、（23），初始干燥土壤的孔隙水压力h0=-260 kPa.通过现场入渗过程监测，饱和的水力传导系数为Ks=1.296 cm/d.根据实测含水率与基质吸力数据，采用VGM 和FX 模型拟合得到的土水特征曲线如图6所示，其确定系数R2分别达到了0.95 和0.98，说明FX 模型具有更好的拟合效果.此外，两种模型的相关拟合参数如表2所示.

图6 不同模型拟合得到的土壤水分特征曲线Fig.6 Soil moisture characteristic curves fitted by different models

表2 不同模型的拟合参数Table 2 Fitting parameters of different models

数值模拟中假设模型深度为60 cm，总模拟时间选择为160 h，空间离散步长 Δz=0.5 cm，时间步长为0.1 h.图7是采用VGM 和FX 模型得到的瞬态孔隙水压力的计算结果，当γ=1 时，两种模型描述的经典Richards 方程所获得的数值解与实测值均存在较大偏差，其中FX 模型得到的数值解（图7（c））相较于VGM 模型得到的数值解（图7（a））偏差更大；当 γ=0.97 时，VGM 模型描述的时间分数阶Richards 方程所获得的数值解可以与实测值吻合得很好（图7（b）），如表3所示，其均方根误差（RSE）和相对误差（RE）均有很大程度的降低.t=24 h时，FX 模型描述的时间分数阶Richards 方程的RSE 和RE 均小于 γ=1的数值，也就是拟合效果有所提高，但其数值解与实测值仍然存在较大偏差（图7（d））.

图7 比较不同SWCC 下不同阶次γ 获得的数值解： （a） VGM 模型，γ=1；（b） VGM 模型，γ=0.97；（c） FX 模型，γ=1；（d） FX 模型，γ=0.97Fig.7 Comparison of the numerical solutions obtained by different orders γ under different SWCC: （a） VGM model,γ=1; （b） VGM model,γ=0.97;（c） FX model,γ=1;（d） FX model,γ=0.97

表3 t=24 h的数值精度Table 3 Numerical accuracy at t=24 h

另外，由于黄土的入渗规律通常接近于经典Richards 方程，因此提出的时间分数阶Richards 方程中阶次γ的取值可以在区间[0.95,1.05]中选择.结果表明，实验中出现的反常扩散现象用VGM 模型的时间分数阶Richards 方程来进行描述是更加合理的，与实测数据具有更好的拟合效果.

3 结 论

本文基于非饱和渗流的Richards 方程，从反常扩散角度引入时间分数阶导数，结合Caputo 导数定义，得到了具有更广泛渗流意义的时间分数阶Richards 方程，并结合土柱入渗实验数据与其数值解进行了对比，得到了如下结论：

1） 时间分数阶Richards 方程具有广泛的适用性，当分数阶阶次γ=1 时，方程退化为经典的Richards 方程，可以描述经典的渗流过程；当分数阶阶次不等于1 时，则可以描述具有反常扩散性质的渗流过程，其中，当γ＜1时，压力水头数值随着 γ的减小而减小，非饱和渗流表现为次扩散，而当 γ＞1时，压力水头数值则随着 γ的增加而增加，表现为超扩散.

2） 从数值结果来看，不同土水特征曲线形式对分数阶阶次敏感程度是不同的，其中Gardner 和FX 模型中所计算的压力水头曲线随着阶次 γ的变化有较大的增幅，而在VGM 模型中所计算的压力水头曲线随着γ的变化有较小的增幅.通过土柱入渗实验，进一步验证了VGM 模型的时间分数阶Richards 方程具有更好的拟合效果，能够更好地描述地下水在非饱和土中的渗流过程.