雷达大下视角下地杂波特性分析

高 希 杜 勇 高晓明

(西安电子工程研究所 西安 710100)

0 引言

在历次战争中，制导武器逐渐成为战场上的焦点，发挥着至关重要的作用。而雷达能够在一定空域内搜索、识别和跟踪目标，常用于导弹制导系统，尤其是主动雷达可不分天气和时间，在较远距离处发现目标，广泛应用于诸多导弹系统中。但是雷达在打击目标过程中，除了会接收到目标信号外，还会接收到幅度高于目标的杂波信号，而且杂波复杂多变，易受环境因素的影响，如地形、风速等等，这些都严重影响着雷达的目标检测性能。

在早期研究中，由于距离分辨率过低，且在低下视角情况下，分辨单元内存在大量独立的随机散射点，但没有起支配作用的强散射点，此时认为杂波满足瑞利分布。但是在实际场景中，毫米波雷达由于分辨率提升，其接收到的杂波特性会由于载体平台姿态改变而变化，文献[2]研究了导弹俯冲飞行时非正侧视雷达下杂波的空时耦合关系，得出导弹在俯冲运动时带来的垂直速度分量会造成多普勒频移与距离相耦合的结论。文献[3]对导弹平飞和俯冲运动时的杂波空时耦合关系也进行了研究，得出相同的结论。

为研究大下视角下地杂波的特性，本文采用假设检验、分布拟合等方法对某毫米波雷达在大下视角下采集的实测地杂波数据进行分析，分析其分布特性，并对其相关性进行了研究，为后续大下视角下杂波抑制算法的研究提供了理论支撑。

1 杂波特性分析方法

杂波分布的研究从瑞利分布开始，随着雷达分辨率的不断提高，许多强散射点被分辨出来，杂波回波出现较大的拖尾效应，此时不再适合使用瑞利分布来描述杂波。于是，Geroge提出并使用对数-正态分布来拟合杂波的幅度特性，且取得了良好的拟合效果。但是由于对数-正态分布的拖尾过长，已不再适合描述瑞利和对数-正态分布之间的杂波，因此Sekine 等人提出了韦布尔分布模型来描述这部分杂波。幅度服从韦布尔分布的模型使用范围较广，适合描述地杂波、海杂波、气象杂波等。随着电磁理论的发展，Jackman通过研究杂波散射机理，得出了 K 分布模型，并对实测数据作拟合分析。K 分布模型在很大程度上反映了杂波的特性，且与实测数据具有良好的吻合性，因此成为杂波常用的分布模型。

这些常用分布的得出既需要通过理论推导，也需要经过实测新数据的验证，而通常需要对实测数据进行以下分析：相关性、时频特性，并使用幅度分布拟合以及假设检验的方法对杂波数据的幅度特性进行分析。

1.1 相关性分析

在时间和空间上，杂波具有一定的关联性，分别称为时间相关性以及空间相关性。其中，时间相关性通常指杂波在同一距离单元通过慢时间积累所展现出来的关联性；而空间相关性指单个快时间内不同距离以及方位单元之间的杂波所展现的关联特性。通过研究杂波的时间相关性和空间相关性，可以研究针对某一地形地貌和相关性来产生服从某一分布的杂波背景，以及在该背景下的杂波抑制和目标检测的算法。

1.2 幅度分布拟合

为了验证杂波数据到底服从经典模型中的哪一种分布模型，需要对杂波数据的幅度进行统计，画出对应的直方图。同时也分别画出与杂波数据具有相同统计特性(分布参数，特征矩)的理论模型的概率密度函数(Probability Density Function，PDF)，包括高斯分布、瑞利分布、对数正态分布、韦布尔分布、K分布。另外，也可从累积分布函数(Cumulative Distribution Function，CDF)出发，统计杂波数据和经典分布的CDF，来进一步说明杂波数据的幅度分布特性。

各种分布的统计特性，如分布参数，可通过最大似然估计法估计杂波参数得到，或者通过计算杂波数据的一阶矩和二阶矩得到，具体如表1所示。

表1 各分布模型的参数估计

1.3 假设检验

通过以上操作，我们只是粗略地选择出了所需杂波符合的概率分布模型，并对杂波模型的参数进行了估计，但没有进行深入的检验分析，因此需要检验模拟数据与理论模型是否一致或假设的分布与实测数据是否贴合。一般分析包括定性分析和定量分析，定性分析可使用直方图或概率密度图将拟合数据和理论模型进行直接对比；而定量分析则在一定假设条件下，计算拟合数据与理论模型的差距来直观对比，常用的方法有χ检验和K-S(Kolmogorov-Smirnov)检验。

131 χ检验

作为一种评判数据拟合优良度的检测方法，检验的检测性能通常被认为是介于质量函数或密度函数与直方图之间。检验既适应于连续分布，也适应于离散分布，在检测过程中都要对检验的统计量进行计算。首先，假设拟合分布的取值范围为[,)，我们将取值范围等间隔划分为个小区间，即[,)、[,)、…[-1,)，其中=，=，且可能取值=-∞，可能取值=+∞。然后，在连续情况下，使用预测分布的密度函数()计算，即

(1)

而在离散情况下，的计算公式为

(2)

其中()是质量函数。

如果定义一组观测样本为,,…,，而为零假设，即假设是一组随机变量，独立同分布，且服从()，()是预测分布的密度函数。同时规定为检测水平，那么可通过以下步骤进行检验：

1)统计出现在个区间的观测值个数，设其数目为，=1,2,…,；

2)对预测分布的观测值按概率出现在各个区间内的期望个数，=1,2,…,进行计算；

3)计算检验的统计值为

(3)

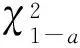
检验过程中最为关键的一点是确定变量的取值范围，即区间。目前，还没有一个明确的方法来选择区间，并对所有的预测分布和样本都有良好的效果。但是仍然可以通过以下原则来对区间进行选择：首先，一般尽可能选择使概率接近于相等的区间，最好情况下使每个区间的都相等。这样做可以让检验更加公平，只有当假设中的真实成分少于虚假成分时，才将其拒绝。其次，选择的区间应使期望的值保持在一定范围，一般≥5。此外，区间的数目应该在30或40以下。

132-检验

K-S(Kolmogorov-Smirnov)检验也可以用来检验数据拟合的优良度，但它通过比较拟合分布函数()与由样本数据值定义的经验分布函数来评估拟合的优良度。在K-S 检验过程中，我们并不需要对样本数据以任何方式进行重组，也就意味着不用再划分区间，也就没有了信息的损失。另外，K-S 检验还有一个特点，它对样本数据的数目没有限制。

在计算K-S检验的统计量之前，我们必须确定经验分布函数()。假设样本数据为,,……，那么经验分布函数()可定义为

(4)

对于所有实数，()是一个右连续的阶梯函数。若()是预测的分布函数，那么数据拟合优良度的评价方法可通过检验()和()之间的相似度来完成。若用来表示K-S检验的统计量，其数值反比于拟合优良度，即当越大时拟合优良度越差。当超过某一个限制点,1-(是显著水平，,1-为分位点)，就认为检验的零假设是错误的，而,1-的大小与假定的分布类型有关。

2 实测数据分析

采集毫米波雷达在大下视角情况下遭遇的地杂波数据作为实测数据，对其中第100帧和第280帧数据进行分析，先对其进行预处理，包括解包和脉冲压缩，脉冲压缩结果如图1所示，左侧为第100帧数据，右侧为第280帧数据。

图1 两帧数据脉压结果

采用动目标检测(MTD)对两帧数据的脉压结果进行分析，得到图3的结果。很明显，由于导弹速度与空间的耦合效应，与静止状态和低下视角下的地杂波相比，大下视角下的地杂波表现为一条斜线。杂波的频谱更宽，不同距离单元的杂波占据的多普勒通道不同，杂波的情况更为复杂，传统通过估计杂波中心去杂波的方法不再适用，杂波抑制的难度加大。

图2 两帧数据MTD结果

对这两帧数据进行PDF和CDF拟合，得到图3和图4的拟合结果。可以看出，大下视角下地杂波与韦布尔分布和正态分布更为接近，但不能说明具体与哪一分布相匹配，还需要通过假设检验进一步验证。

图3 第100帧数据拟合结果

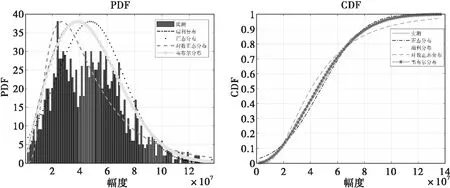
图4 第280帧数据拟合结果

两组数据的时间相关性和空间相关性结果如图5和图6所示。可以看出，大下视角下的地杂波具有秒级的时间相关性，每个雷达相参处理周期内每个距离是相关的；但大下视角下的地杂波的空间相关性很低，相邻距离单元之间相互独立，不存在相关性。

图5 第100帧数据相关性

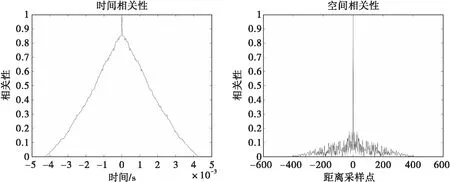
图6 第280帧数据相关性

采用卡方检验对PDF和CDF拟合结果进行进一步验证，结果如表3示。对这两帧数据采用5%显著水平进行检验，结果表明大下视角下的地杂波服从韦布尔分布，可见，虽然杂波背景都是戈壁区域，但由于雷达运动姿态的改变，在大下视角下，地杂波不再服从瑞利分布，杂波散射点不再保持同一水平，强散射点所占的比例增加，杂波分布由均匀变得不均匀，而传统的单元平均恒虚警检测器无法将这些强散射点抑制，这些都影响了雷达的目标检测性能。

表2 5%显著水平卡方检验结果

3 结束语

通过对大下视角下地杂波的实测数据进行分析，可以看出由于雷达运动姿态和照射区域地形的变化，地杂波回波中的强散射点出现的概率增大，整体上由均匀变得非均匀，逐渐偏离瑞利分布，服从韦布尔分布，导致传统的单元平均恒虚警检测器不再适用，应采用非均匀环境下的检测器，如排序类检测器、单元选大恒虚警检测器、智能检测器等。

这样，为非均匀杂波环境中的目标检测和杂波抑制算法提供了理论依据。在后续的杂波抑制算法设计中，可以重点研究非均匀杂波环境下的目标检测算法，为提高大下视角下雷达的检测性能提供理论支撑。