主动拦截防护系统坐标变换方法研究
刘昭涛 陈日明 黄家露
(中国北方车辆研究所 北京 100072)
0 引言
主动拦截防护系统是新一代坦克装甲车辆综合防护系统中的重要组成部分,其属于硬杀伤防护系统,用于在敌方反坦克弹药击中车辆前对其进行摧毁拦截。该系统主要由三部分组成:第一部分为超近程探测雷达,负责精确测量来袭目标的运动参数;第二部分为主控制器,负责外推来袭目标的弹道、计算拦截点并控制发射转台将拦截弹药对准来袭目标并进行点火发射;第三部分为转台及拦截弹药,负责响应主控制器的决策并可靠发射对来袭目标进行摧毁。
为了实现对坦克装甲车辆的全方位防护,通常需要在车体不同方位上安装多部超近程探测雷达。同时,为了实现精确拦截,发射转台需要控制拦截弹药发射的角度。因此需要对主动拦截防护系统的多部超近程探测雷达与发射转台进行坐标变换。
1 主动拦截防护系统中的坐标系
新一代坦克装甲车辆主动拦截防护系统的工作流程如图1所示。分布在车体四周的多部超近程探测雷达对周边空域进行边搜索边跟踪,当发现有来袭目标时立刻进行数据预处理并将航迹数据上报至主控制器;主控制器通过航迹数据进行威胁判断与决策,计算得到发射转台应该调转的方位角和俯仰角,以及相应拦截弹药的点火时刻并给出点火信号;拦截弹药在收到点火信号后进行发射,对来袭目标进行毁伤。

图1 主动拦截防护系统工作流程
以国外公开的主动拦截防护系统为例,其安装俯视示意如图2所示。

图2 主动拦截防护系统安装俯视图
由图2可以看出,主动拦截防护系统的四部超近程探测雷达和一部发射转台安装在坦克的炮塔上,可以随炮塔转动。四部雷达探测不同的区域,组合起来可以实现车体四周360°全覆盖;发射转台为随动式二维转台,可以控制拦截弹药在方位向和俯仰向进行转动,实现相应的拦截位置指向。
超近程探测雷达测量目标的坐标系为球面坐标系,其在直角坐标系下的关系如图3所示。其中轴方向为雷达阵面法线方向(方位角俯仰角均为0),轴方向为方位角90°方向,轴方向为俯仰角90°方向。

图3 雷达测量坐标系
设某一雷达(=1,2,3,4)测量点的距离为,方位角为,俯仰角为,考虑到轴方向为雷达方位角90°方向,可以得到雷达测量坐标系与空间直角坐标系的关系如式(1)所示。四部超近程探测雷达的测量球面坐标系的原点为相应雷达阵面法线的起点,其与空间直角坐标系的关系均为式(1)所示。
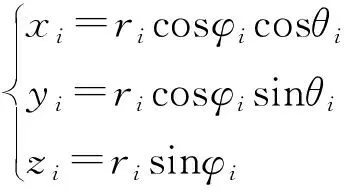
(1)
发射转台为二维转台,其瞄准坐标系亦为球面坐标系,可以规定发射转台旋转中心为0点,沿坦克炮管方向瞄准时为轴方向,发射转台旋转方位角90°(俯视沿炮管向左90°)为轴方向,发射转台俯仰角90°为轴方向。那么,发射转台瞄准坐标系一点的距离为,方位角为,俯仰角为,与其空间直角坐标系(,,)的关系亦为式(1)。数学上易得发射转台空间直角坐标系到其瞄准球面坐标系的关系如式(2)所示。

(2)
在主动拦截防护系统工作时,为了使发射转台精确地指向来袭目标的位置,需要将在雷达测量坐标系下的航迹数据变换到发射转台瞄准坐标系下,然后再进行滤波和外推。因此考虑先将雷达测量球面坐标系由式(1)变换到空间直角坐标系,然后通过坐标系的平移和旋转转换到发射转台的空间直角坐标系下,最后再由式(2)变换至发射转台的瞄准球坐标系下。
考虑直角坐标系下空间一点(,,),将其坐标系沿轴正方向平移一段距离,则其在新的坐标系中的坐标(′,′,′)可由矩阵形式(3)给出。

(3)
其中为沿轴平移的变换矩阵。类似的可以得出沿轴平移距离的平移变换矩阵,以及沿轴平移距离的平移变换矩阵如式(4)、式(5)所示。

(4)

(5)
考虑直角坐标系下空间一点(,,),以轴正方向为轴线,将其坐标系向右手法则确定的正方向旋转一个角度,则其在新的坐标系中的坐标(′,′,′)可由矩阵形式(6)给出。

(6)
其中为沿轴旋转的变换矩阵。类似的可以得出沿轴旋转角度的旋转变换矩阵,以及沿轴旋转角度的旋转变换矩阵如式(7)所示。

(7)

(8)
那么,某一空间直角坐标系中的一点=[1]经坐标的平移和旋转后,在另一空间直角坐标系中的坐标′一般形式为
′=
(9)
式(9)中坐标变换过程中相乘的矩阵可以定义为空间直角坐标系的变换矩阵。那么,只要确定了主动拦截防护系统中的每部超近程探测雷达与发射转台之间的坐标变换矩阵,就可以通过式(9)得到发射转台坐标系下的来袭目标航迹。
2 变换矩阵的求解
当主动拦截防护系统在车体上安装好之后,每部超近程探测雷达与发射转台的坐标变换矩阵就已经确定了。但系统安装在坦克装甲车辆上时,其各个方向的旋转量和平移量不容易准确测量得出,因此我们考虑用两个坐标系下测量若干个共同观测点坐标的方法确定不同雷达相对于发射转台的变换矩阵。将式(9)重新写成式(10)形式。
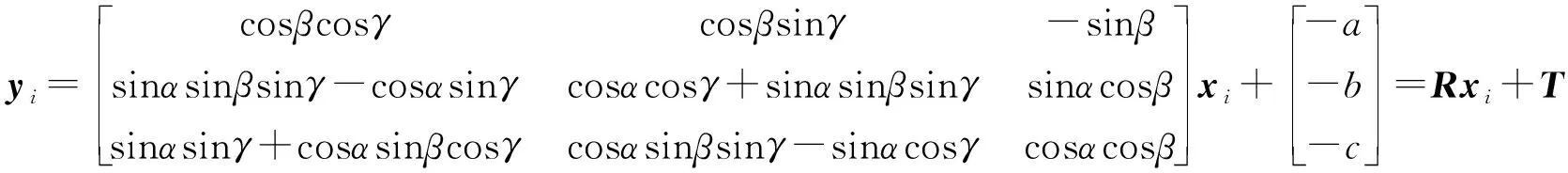
(10)
其中,为三阶旋转变换矩阵,为平移向量,=[]、=[′′′]分别为雷达坐标系和发射平台坐标系下对应点的坐标,则给出不共线的三组对应点坐标,即可确定坐标变换矩阵。
在工程实践中,我们可以利用目标模拟器在雷达远处产生一个固定目标,读取相应的雷达观测点的距离、方位角、俯仰角,并利用式(1)解算出其在直角坐标系中的坐标;同时,在发射转台上安装瞄准镜和测距仪,读取瞄准镜观测目标模拟器发射天线时转台的方位角与俯仰角,并利用测距仪测量转台到目标模拟器发射天线的距离,然后利用式(1)解算出其在直角坐标系中的坐标。这样就可以得到一组共同观测点的坐标和。超近程探测雷达与发射转台共同观测点的测量方法如图4所示。
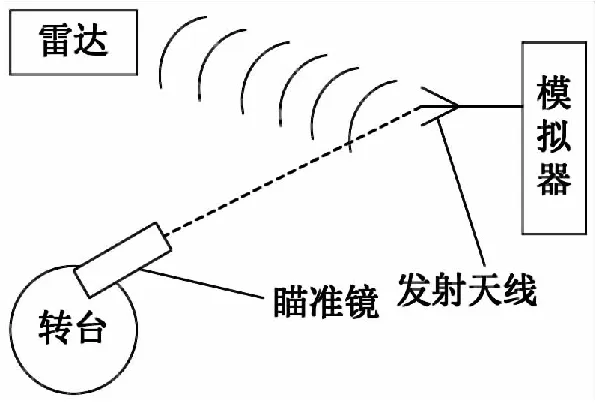
图4 共同观测点测量方法
由于实际测量中误差的引入,对每部雷达应取尽可能多的观测点,对式(10)进行最小二乘拟合,从而求解出坐标变换矩阵。此时,最小二乘问题如式(11)所示。
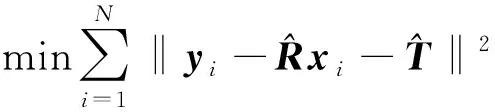
(11)
令
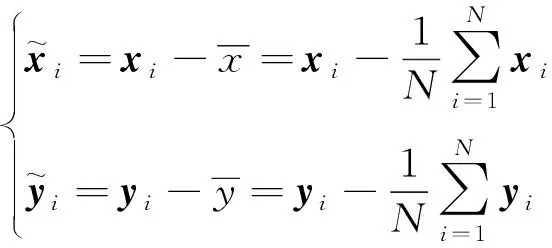
(12)
则根据最小二乘解的性质,式(11)等价于

(13)
令

(14)
则式(13)等价于最大化矩阵的迹为
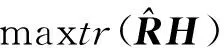
(15)
对奇异值分解为=,易得满足式(15)的旋转矩阵估计值为
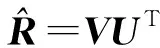
(16)
则平移向量估计值为

(17)
通过上述分析,我们可以总结出主动拦截防护系统坐标变换矩阵的求解方法如下:
1)在主动拦截防护系统安装完成后,利用目标模拟器,测出每部雷达与发射转台的若干组共同观测点;
2)用式(1)求得共同观测点分别在雷达和发射转台直角坐标系下的坐标值;
3)用式(16)~式(17)求出每部雷达相对于发射转台的坐标变换矩阵。
当主动拦截防护系统工作时,主控制器收到雷达上报的航迹数据,先用式(1)变换成相应的空间直角坐标系,再通过对应雷达的变换矩阵,利用式(10)求出来袭目标在发射转台直角坐标系下的坐标,最后用式(2)将其变换为发射平台瞄准球坐标系下的位置。当同时有两部雷达观测到来袭目标时,两部雷达通过各自的变换矩阵求得目标在转台坐标下的坐标值,然后再进行目标数据融合并进行数据处理。
3 实测数据
结合上节所述的方法,我们在某模拟平台上对某型主动拦截防护系统进行了数据实测。用目标模拟器对某一安装位置的超近程探测雷达与发射转台进行了3个共同观测点的测量,其测量值如表1所示。

表1 共同观测点测量值
利用上节述所方法可以求得旋转矩阵和平移向量。其中

(18)

(19)
随后,对主动拦截防护系统进行模拟目标探测试验,得到超近程探测雷达的目标测量值和经坐标变换后发射转台瞄准方向如图5所示。
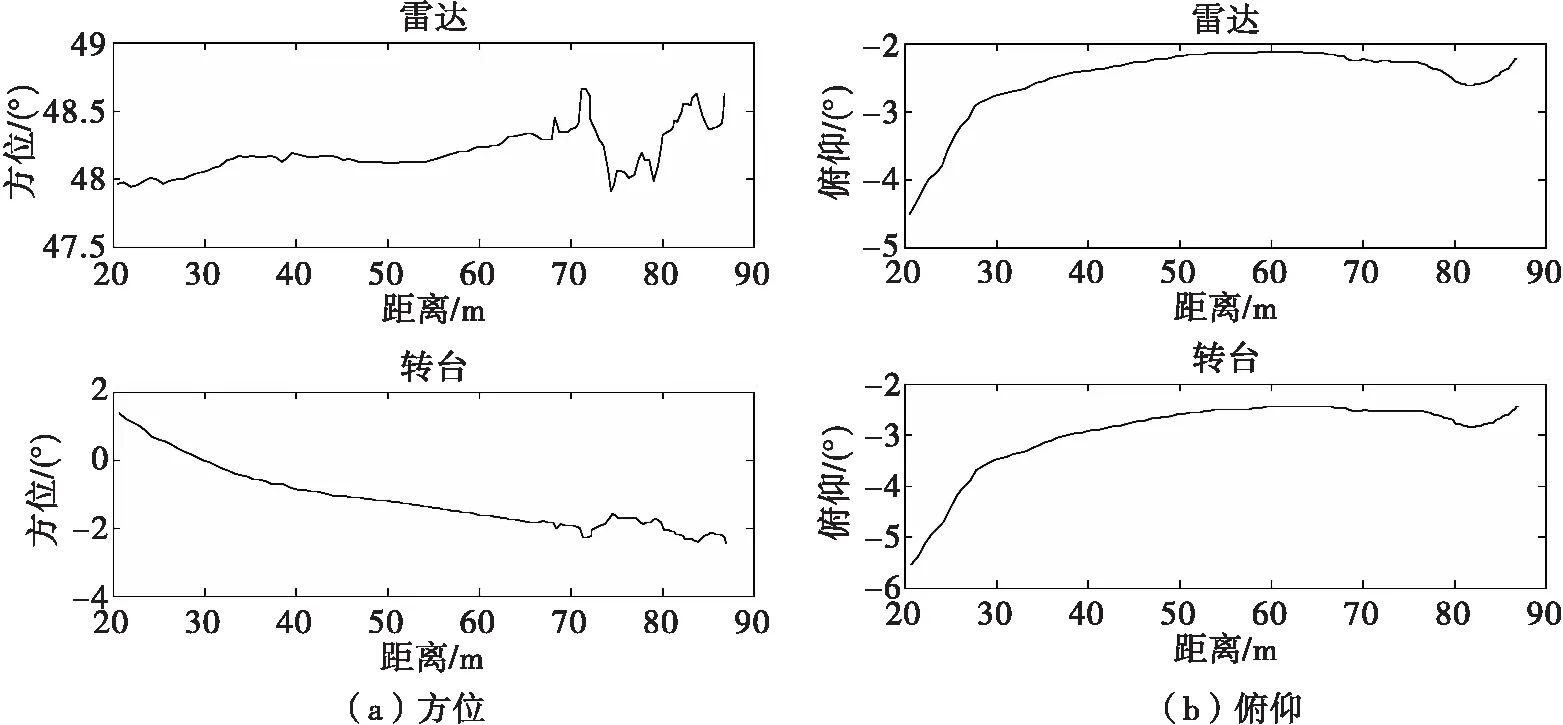
图5 雷达与转台的方位和俯仰
经实际测量,上节所述坐标变换方法能够使主动拦截防护系统发射转台可靠指向雷达上报的目标来袭方向。
4 结束语
坦克装甲车辆主动拦截防护系统是一个小型的超近程反导系统,其中多部超近程探测雷达与发射转台需要进行坐标变换以进行准确拦截。在分析了探测雷达和发射转台各自的坐标系后,对其坐标变换矩阵的公式进行了推导。并给出了实际工作中求解坐标变换矩阵的方法,以及主动防护拦截系统应用坐标变换的工作流程。该方法已经在某型主动拦截防护系统中得到了应用。

