基于塑性变形能与改进动量法的交通事故参数计算

陈家涌，吴新烨

（厦门大学 建筑与土木工程学院，厦门市交通基础设施智能管养工程技术研究中心，厦门 361005，中国）

车辆碰撞容易翻滚、爆炸等问题，从而造成重大的安全问题、经济损失。交通事故重建的目的是能够客观科学的对道路交通事故进行重现，提高交通事故判定的准确性、公正性、科学性，目前交通事故重建主要有动量法、能量法2 种模型。20 世纪90 年代，Ishikawa 基于碰撞中两车的动量、动量矩、恢复因数而建立了动量法模型来进行汽车交通事故重建[1-2]。Herman Stcffan 以Kudlich-Slibar 的模型开发了PC-Crash 软件，并基于动量理论引入切向、法向恢复因数来构建模型。

清华大学在国内较早开展了相关研究，李一兵发现了基于动量法的事故再现模型中计算结果的参数敏感性问题[3]以及事故再现估计速度不确定性的问题[4]。陈涛等人基于动量法模型对车辆碰撞事故中参数进行分析，得知在接近正面碰撞的工况下，碰撞方位角对结果的影响尤为重大[5]。郑月楠基于动量法模型，对碰撞后车辆运动轨迹计算过程进行优化，证明了基于动力学迭代求解碰撞后运动参数的可行性[6]。

陈昆山通过将Ishikawa 的动量法模型应用于一起无轨迹碰撞事故，并利用LS-DYNA 软件进行整车碰撞仿真，发现能够较好的对碰撞前车速进行反求[7]。张健基于动量法模型对实际事故案例展开研究，分析碰撞中心坐标、力学参数、转动惯量等参数的误差对碰撞前车辆运动参数的影响，并得到了事故重建中速度误差与上述几种参数之间的关系[8-11]。

王金刚较早的基于车辆能量网格与能量法模型展开研究，并将其应用于实际的交通事故还原中[12]。王旭东对车辆侧向碰撞事故中的车辆刚度系数误差展开研究，并提出了有效的解决方法[13]。刘志强[14]则将能量法模型应用于一起车辆侧向碰撞事故，发现模型的计算结果与Vangi[15]提出的推荐公式所得到的计算结果相吻合。

邹铁方利用PC-crash 软件设计正交实验，对交通事故重建中参数的敏感性进行了研究[16]。胡林等人通过Madyom 动力学软件对交通事故重建中人体头部的损伤差异性进行了探究[17]。

目前采用动量法模型进行事故重建时，选取碰撞前后的恢复因数遇到一定的困难，进而造成计算误差。本文通过对比碰撞过程中的能量损失与车体的塑性变形能，完成基于塑性变形能的车辆二维点碰撞动量法模型构建，从而有效避免切向法向恢复因数选取的主观性和不确定性，探究将车辆塑性变形能应用于车辆二维点碰撞动量法交通事故重建的可行性与有效性。

1 车辆二维点碰撞的力学分析

1.1 二维点碰撞模型的建立

在大部分碰撞事故中，碰撞前两车位置是错位的；大部分车辆在碰撞后都会有一定程度转动的情况，故车辆之间的碰撞一般为二维碰撞。本文探究车辆的一般二维点碰撞，利用车辆之间的动量、动量矩、切向法向恢复因数建立动量法模型[1-2]。

以两车的碰撞点为原点O，并以其切线（tangent,T）、法线(normal,N)方向建立直角坐标系。其中a1、b1、a2、b2分别为车1与车2 的质心在坐标系里的位置参数；车1 速度沿着T、N2 轴的速度分量为v10T、v10N，角速度为ω1；车2 速度T、N2 轴的速度分量为v20T、v20N，角速度为ω2。

车辆发生一般二维点碰撞示意图见图1。

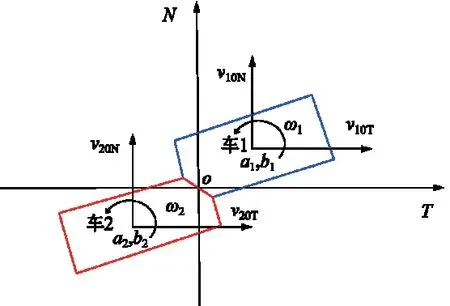
图1 车辆发生一般二维点碰撞示意图

车辆与车辆的碰撞过程分为碰撞前、碰撞中、碰撞后3 个过程，碰撞中过程持续时间极其短暂并产生较大的碰撞力，一般只有60～150 ms 左右。在短暂的时间内，两车完成速度上的交换，因此在碰撞中阶段往往可以忽略摩擦力做功、空气阻力作用、噪声发热等外力作用与能量损耗。

以车1、车2 为研究对象，通过动量定理可以得到：

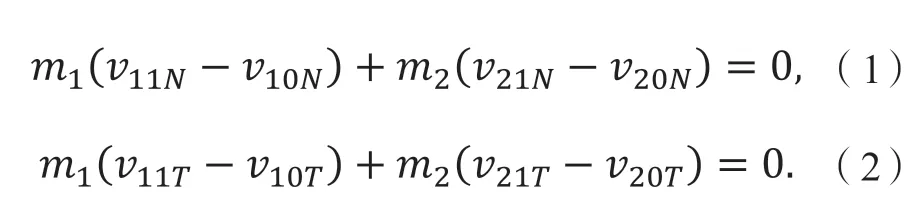
其中：mi为车身的质量(i=1，2，分别代表车1 和车2)，vijk为速度分量（j=0、1，分别代表碰撞前和碰撞后；k的取值为N轴或者T轴）。

以车1、车2 为研究对象，对坐标原点O取动量矩，通过动量矩定理可以得到：

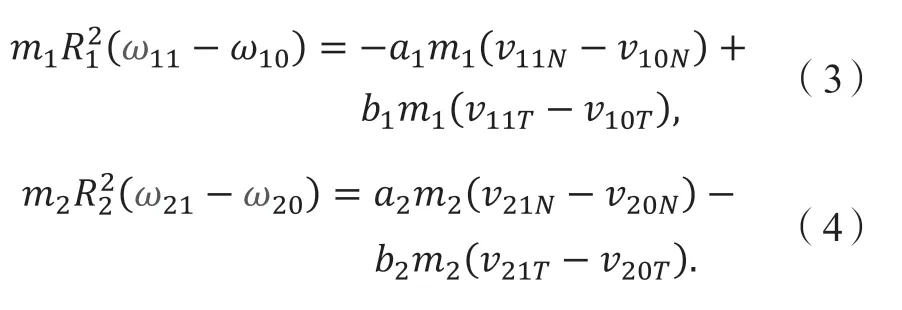
其中：ωij为车辆的角速度，R1、R2分别为车1 与车2 的转动半径，而车1 与车2 的质心位置在坐标系内的坐标分别为（a1,b1）、（a2,b2）。

1.2 引入切向与法向恢复因数对方程组重构

考察碰撞后的运动参数：相对变形速度（relative deformation speed，RDS）和相对滑动速度 (relative sliding speed，RSS)，以及碰撞前的运动参数：RDS0和RSS0，定义为：

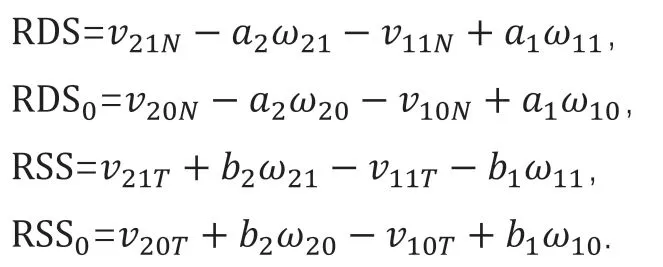
由于运动状态参数多于约束方程的个数，引进切向、法向恢复因数eN、eT对方程进行补充：

结合式（1）-（6），碰撞前后运动参数表达为

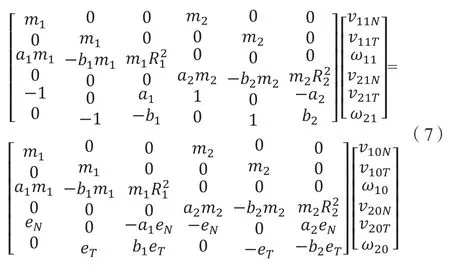
2 基于塑性变形能的动量法模型构建

2.1 碰撞过程中的能量变化及车辆的塑性变形能

因碰撞接触到碰撞分离的时间很短，故忽略空气动力、摩檫力等外界因素的影响。在2 车碰撞前，2 车的合动能达到最大。在碰撞中当2 车达到共同速度时，2车合动能的损失达到最大，此时弹性变形、弹性势能最大；而后随着2 车开始分离，弹性变形减少并且一部分弹性势能又转变为动能。2 车的合动能在碰撞过程中的能量变化如图2 所示。其中：Ein为2 车接触碰撞前的动能之和；Eout为2 车将要分离瞬间的动能之和。若令EL为2 车碰撞前与碰撞后损失(loss,L)的动能，则ELmax为整个碰撞中阶段的最大动能损失。

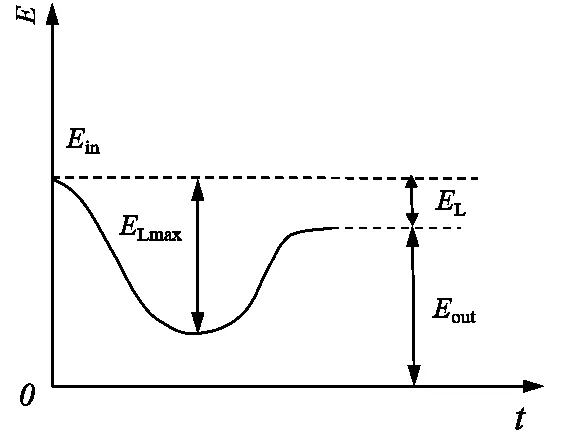
图2 车辆能量随碰撞过程变化图

显而易见：

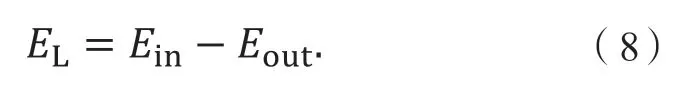
在实车碰撞实验中发现，车辆所受单位宽度上的碰撞力与车辆的变形量呈线性变化关系[18-19]：

其中：F为车体单位宽度上所受的碰撞力，其方向与宽度垂直；W为碰撞力对应的宽度，A为没有塑性变形时单位宽度上的碰撞力，B为斜率，C为车辆宽度上某位置的变形量。

常数A、B与车辆类型有关，美国国家公路交通安全管理局（National Highway Traffic Safety Administration，NHTSA）在对大量车辆碰撞实验的基础上，对所得碰撞试验数据进行线性回归统计得到的参数。该公式虽然因为较为简单应用广泛，但不适用于高速车辆碰撞的情况，在高速碰撞下常数A、B可能会有较为明显的下降[20]。

碰撞后车辆产生塑性变形如图3 所示。其中：Y为车身的长度方向；W为车身的宽度方向；C1—C6为车身宽度上5 等分各端点处的塑性变形值。

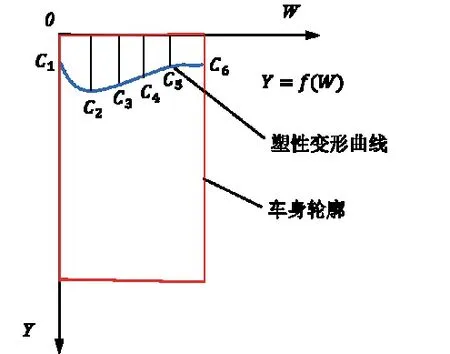
图3 车辆塑性变形示意图

对式（9）在车辆宽度以及塑性变形上进行2 次积分，可得到车辆的塑性变形能为

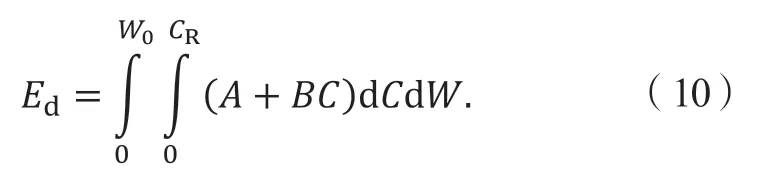
其中：C为宽度任一位置上的塑性变形，W0为车体宽度，而CR为车辆上的变形曲线。

在将车辆二维点碰撞模型与车辆塑性变形能公式两者结合以构建改进模型时，假设：

1）两车在碰撞后不发生二次事故，即车辆在碰撞后不发生翻滚、侧翻、倾覆等二次碰撞事故。

2）两车在碰撞过程中车辆质心高度差距较小，并且碰撞速度相对在中低速范围内，不产生竖向动能损失。

3）考虑到在碰撞前后两车的能量应守恒，可以认为两车碰撞过程中的最终能量损失EL就是两车的塑性变形能Ed，即：

2.2 车辆塑性变形能与动量法模型的结合

动量法模型中两车碰撞前后能量损失EL可通过两车碰撞前后动能差值计算[2]：

而且，γ1N、γ1T、γ2N、γ2T、mN、mT、m0为等效参数，R1、R2分别为车1 与车2 的转动半径。结合式（11）、（12），得到车辆变形C、碰撞前后恢复因数eN与eT、碰撞后运动参数RDS 与RSS 之间的关系：

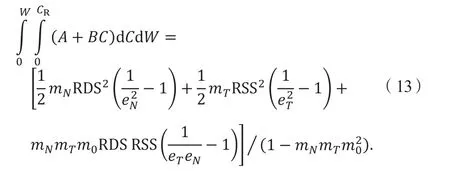
通过式（13）得到eN与eT的关系，并通过eN循环计算，并以此计算两车碰撞前后理论上的能量损失。由于忽略了碰撞中的能量损失，故理论计算的车辆能量损失与车辆的塑性变形能Ed相等，即：

3 数值模拟与验证

3.1 事故现场情况及碰撞后运动参数计算

某天下午一辆大众轿车由西向东行驶，此时一辆自东向西的长安轿车越过路中心线，两车相撞。根据痕迹，两车碰撞的角度非常大，接近于正面非对心碰撞，碰撞前两车都没有采取制动措施，事故现场如图4 所示[21]。

图4 道路交通事故示意图[21]

通过从该事故中测量到的相关数据[21]，得到车辆基本参数与车辆塑性变形量，通过平均塑性变形计算车辆塑性变形能Ed。通过式（11）算得Ed=119.4 kJ。将车辆相关参数列于表1，其中：C1—C6为车辆的变形量，W0为变形宽度。

表1 车辆基本参数与质心位置参数

2 车在碰撞后分离阶段，车辆运动参数、速度方向决定了2 车最终停止位置。基于车辆分离瞬间与车辆停止时2 车的质心位置，通过刚体动力学迭代得到2 车理论计算的停止位置。将理论计算停止位置、实际停止位置相对比，确定2 车碰撞后分离瞬间的运动参数[6]。计算流程图如图5 所示，并将计算结果列于表2。

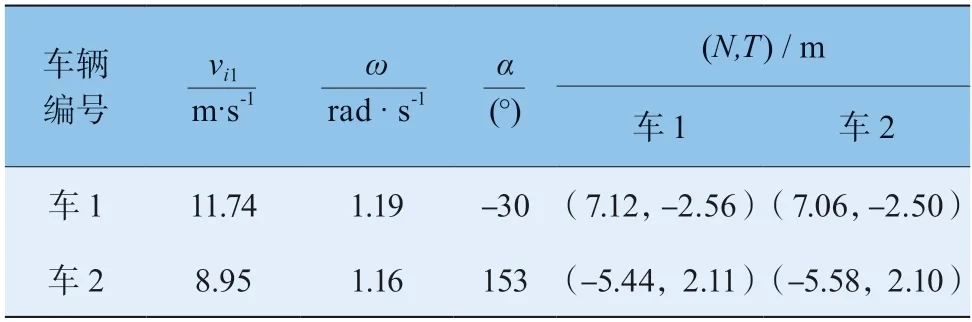
表2 碰撞后2 车运动参数计算

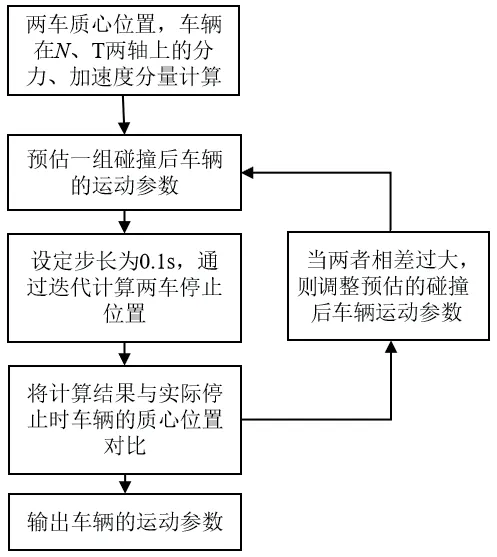
图5 碰撞后运动参数计算流程图

3.2 能量法模型计算

假设2 车对撞时只存在线速度，忽略角速度，利用水平方向能量守恒、碰撞冲量与n轴的夹角、以及塑性变形能Ed为约束条件，构建能量法计算模型[14，22]。计算可得：车1 和车2 碰撞前速度分别为52.6 km/h 和47.6 km/h。碰撞前后2 车能量损失为122.5 kJ，其与塑性变形能的相对误差为2.57%。

3.3 基于车辆塑性变形能的能量法模型计算

将车辆塑性变形能Ed作为约束条件，对于任个给定法向恢复因数eN，都能得到一组车辆碰撞前运动参数(vi0、ω)以及车辆的理论塑性变形能。通过循环计算，避免切向法向恢复因数选取的主观性和不确定性问题，可以得到相对准确的结果。计算流程如图6 所示。

图6 计算流程图

以车辆塑性变形能的动量法模型所得2 车碰撞前运动参数如下：车1 和车2 的速度分别为53.9 km/h 和46.5 km/h，角速度分别为0.26 rad/s 和-0.18 rad/s，碰撞前后两车能量损失为125.4 kJ，其与塑性变形能的相对误差为5.04%。

3.4 PC-crash 仿真结果

在PC-crash 软件内设置车辆质心高度、减速阶段减速度后，调整2 车碰撞前运动参数、碰撞点位置、碰撞角度、恢复因数等参数，使得PC-crash 仿真软件内车辆的停止位置与实际停止位置接近。2 车摩擦因数μ=0.7，反弹因数λ=0.1，其余参数设置列于表3，仿真与实际中车辆的停止位置如图7 所示。

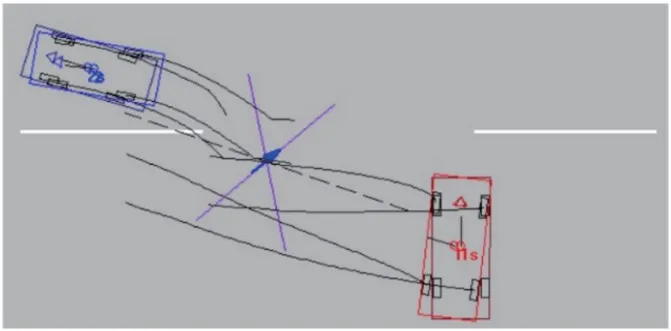
图7 PC-crash 仿真结果

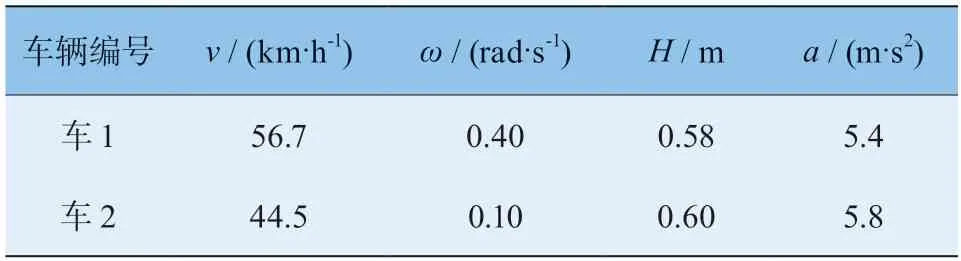
表3 PC-crash 中碰撞冲量及其他参数设置

PC-crash 软件仿真中，采用的是案例中的长安轿车与大众轿车，车高均在1.6～1.7 m 左右，2 车的质心高度基本相等。因此本文案例中采取的改进算法将情况设定在中低速度并忽略竖向动能损耗，对车辆碰撞瞬间前的运动参数进行计算是合理的。

通过测量PC-crash 软件中2 车停止时的质心位置坐标，其与实际2 车停止时的质心坐标相近，因此将PC-crash 软件的计算结果认为是2 车实际发生碰撞前的速度。仿真所得2 车停止时质心位置列于表4。

表4 PC-crash 计算2 车停止位置结果

3.4 数据分析

现将PC-Crash 软件模拟、能量法以及本文的基于塑性变形能的车辆二维点碰撞改进的动量法所计算得到碰撞后2 车运动参数汇总于表5，其中，δ为能量法、本文模型与PC-Crash 的速度相对误差。

表5 不同模型计算结果汇总表

可以看出：基于塑性变形能的车辆二维点碰撞动量法的计算结果与PC-crash、能量法计算模型得到的结果较为吻合，这说明：基于塑性变形能的车辆二维点碰撞动量法计算结果比较合理。

分析可知：基于塑性变形能的车辆二维点碰撞动量法能够一定程度提高计算精度。

有如下分析：

1）常规的能量法模型中，由于矩阵内多个方程之间可能存在线性相关、方程之间数量级相差过大，进而容易导致方程组的解存在病态现象[22-23]。在利用基于塑性变形能的车辆二维点碰撞动量法求解碰撞前运动参数之前，通过检验发现本案例中6 个方程在代数空间内得夹角较大，不存在因为方程间夹角较小而导致碰撞后运动参数、切向法向恢复因数对解的结果影响过大情况。

2）能量法模型忽略了正面碰撞过程中的角速度，导致两车碰撞前原本存在的微小转动动能转化为平动动能，进而导致2 车碰撞前线速度误差过大。基于塑性变形能的车辆二维点碰撞动量法在计算时考虑了碰撞前2 车可能存在的角速度，因此计算结果合理。

3）与其他模型相比，本文中提出的改进模型在计算车辆碰撞分离前瞬间的运动参数具有较好的结果，但改进模型在进行推导时未对2 车碰撞产生竖向动能的损耗进行探究。

4 结论

本文将车辆碰撞后的塑性变形能作为参数，引入到动量法模型中进行碰撞前的运动参数计算，构建基于车辆塑性变形能与改进动量法的交通事故参数计算模型。该计算模型可以避免切向、法向恢复因数选取的主观性以及不确定性等问题。由于改进模型在计算中考虑了2 车碰撞前的角速度，通过对比基于塑性变形能的车辆二维点碰撞动量法的计算结果与PC-crash软件仿真结果、能量法模型计算结果发现：改进模型的计算结果与PC-crash 软件仿真结果较为接近，改进模型的计算结果与能量法的计算结果相比，更加接近车辆正面非对心碰撞事故发生的情况。