新型波纹结构吸能盒耐撞性研究

罗 耿，赵剑南，陈 亮，柴成鹏，王 童，陈轶嵩*

（1.长安大学 汽车学院，西安710064，中国；2.湖南大学，汽车车身先进设计制造国家重点实验室，长沙410082，中国）

为了提高车辆被动安全性，高效吸能缓冲材料与结构已经引起研究人员广泛的关注。薄壁结构由于结构简单，能量吸收效果优异，变形模式稳定等突出优点备受青睐[1]，已在车辆吸能盒上得到了广泛的研究与应用[2-5]。早期关于薄壁结构的研究大多聚集于方管、圆管等规则薄壁结构。这类薄壁结构具有坍塌模式稳定、吸能效果好等优点。但是，这类简单薄壁结构往往初始峰值载荷过大，压溃力的波动过大，并不利于汽车安全性能的提升。因此，研究人员在管体上设计了触发结构，如设置凹痕、孔洞、折痕、波纹等。研究表明，触发结构可以使管体从预先设计的薄弱处被压溃，进而引导整个管体的变形进程；波纹相较于凹槽和孔洞等诱导结构在引导变形方面有着更为出色的表现，能使薄壁管的变形过程更为平稳[6]。对此，大量的研究工作围绕着波纹薄壁结构展开。如：A.Singace[7]通过实验的方式研究了波纹管能量吸收特性，结果表明引入波纹使得载荷—位移曲线更为平缓；D.H.Chen[8]首次使用有限元法研究了波纹对圆管变形模式的影响，结果表明波纹是影响变形模式和载荷—位移曲线的主要因素之一，波纹参数与结构吸能特性之间的关系也被详细讨论。WU Chengyin[9]提出了一种正弦波型波纹管，研究了正弦波的幅值和周期等参数对变形模式的影响，结构表明正弦波型波纹管可以有效降低初始峰值载荷；I.Takuma[10]研究发现波纹管的坍塌模式对波形曲率极为敏感。M.M.Nalla 研究了波纹数量和波纹位置对波纹管耐撞性的影响，发现与传统圆管相比初始峰值载荷降低了42.17%[11]。刘尧庆研究了TRB 波纹管结构参数对吸能特性的影响，研究发现过渡区厚度差对吸能效果影响最为明显[12]。此外，还有研究人员对纵向波纹管开展了研究[13-16]，对波纹管在轴向压缩载荷作用下的变形模式进行了详细地讨论，将波纹管的变形模式分为非稳定变形模式、混合模式、钻石模式和轴对称模式。

虽然波纹管的波纹设计已经较为完善，但是在其变形过程中，初始峰值载荷仍然较高，冲击过程仍不够平稳。为了解决上述问题，研究者们提出了一系列新型波纹结构。E.S.Alkhatib[17]在锥形管上设置波纹结构，结果表明冲击力显著降低。S.Rawat[18]、D.Agrawal[19]和姚曙光[20]分析了梯度波长或梯度幅值的正弦波纹对管能量吸收特性的影响，结果表明功能梯度波纹管比均匀波纹管表现出更好的耐撞性，特别是比吸能增加了21%～57%，平均冲击力增加了15%～45%。以上研究虽然采取种种方式以期使波纹结构的耐撞性更优，但波纹本质上仍是相互独立，耐撞性能仍有提升空间。

因此，基于以上研究，本文设计并提出了一种新型连续波纹管(equidistant continual corrugated tube，ECCT)铝合金吸能盒，并与传统等距离散波纹管(equidistant discrete corrugated tube，EDCT)进行了对比研究，详细分析波纹幅值、波纹数目、壁厚等结构参数对吸能特性与变形模式的影响，并开展基于耐撞性的多目标优化设计。

1 研究方法

1.1 EDCT 和ECCT 的几何模型

本文采用余弦函数来描述管的波纹形状：

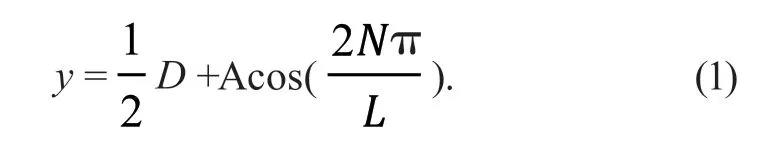
其中：x为距离坐标轴圆点的横向距离，N为波纹数量，A为波纹幅值，L为波纹管长度，D为波纹管直径。图1为A=2 mm，N=16 时的EDCT 波纹图样。

图1 EDCT 波纹图样(A=2 mm，N=16)在ECCT 结构中，采用螺旋线将波纹连接，螺旋线参数方程为：

其中：x、y、z分别为3 条坐标轴的坐标值，θ为与原点的横向距离，ECCT 如图2 所示。

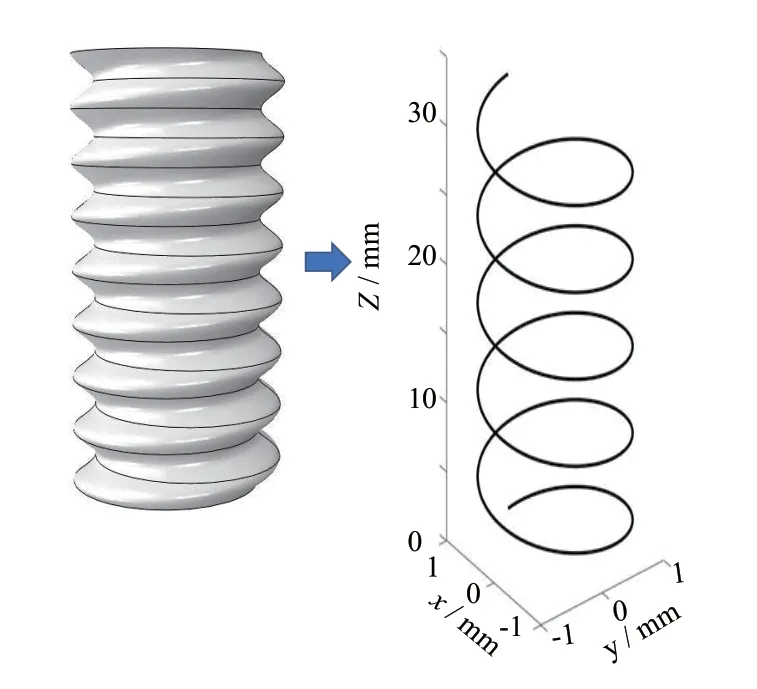
图2 ECCT 示意图

为了研究结构参数对薄壁管吸能特性和变形模式的影响，本文令波纹数在2～16 间变化（步长为2），波纹幅值在0.5～4 mm 间变化（步长为0.5 mm），波纹从离散到连续变化。这样三者相互组合，可以得到128 种不同参数的波纹管。为了方便叙述，采用A代表波纹幅值，N代表波纹数目，例如，A1N4-EDCT 代表幅值为1 mm，波纹数为4 的等距离散波纹管。本文中每个薄壁管的轴向长度L=100 mm，平均直径D=50 mm；如果未作说明，壁厚H=1 mm。

1.2 吸能指标

基于能量吸收结构在轴向压缩载荷作用下的载荷—位移响应，本文按参考文献[21]定义用于评价波纹结构耐撞性的指标。

总吸能（energy absorption,EA)代表碰撞过程中薄壁结构实际吸收能量，可由式(3)计算得出：

其中：F(δ)是瞬时压溃力，是压溃过程中位移δ的函数;δ是有效变形距离。

比吸能（specific energy absorption,SEA）表示结构单位质量吸收的能量，根据式(4)计算得到：

其中，m是能量吸收器的质量。

初始峰值载荷（initial peak crush force,IPCF）表示在冲击过程的有效压缩冲程期间薄壁管中的最大瞬时冲击力。

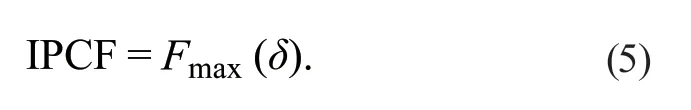
平均压溃力（mean crushing force,MCF）表示在整个变形行程中，载荷的平均水平。

其中δ代表有效行程。

冲击效率（crush force efficiency,CFE）等于平均压溃力与初始峰值载荷的比值。

承载波动系数（undulation of load-carrying capacity,ULC）是从能量角度评价冲击力波动程度的指标，其表达式如下：

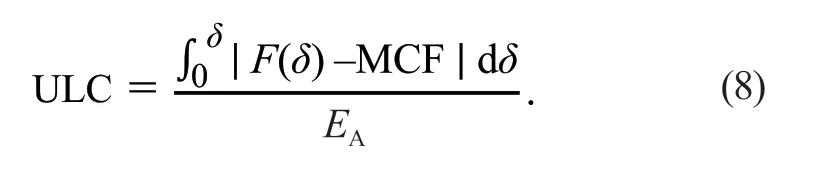
2 有限元模型的建立与验证

2.1 材料模型

本文中EDCT 和ECCT 选用铝合金AA6061-O，其材料参数见表1，选用有限元分析软件Abaqus 中的Elastic 和Plastic 材料模型。

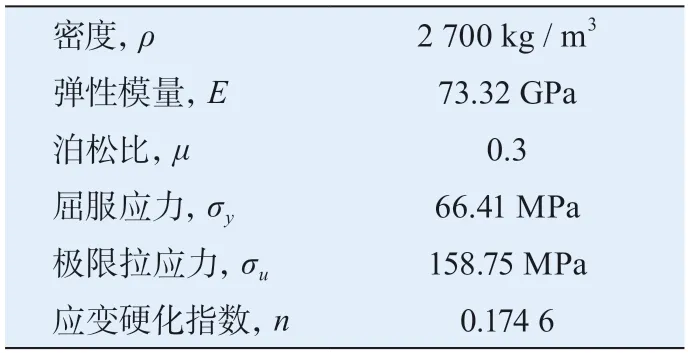
表1 AA6061-O 铝合金材料参数[22]

2.2 有限元模型的建立

使用有限元分析软件Abaqus 建立波纹管的有限元模型。为了在保证计算精度的前提下，尽可能地节省计算资源，经过网格尺寸灵敏性分析，全局网格尺寸选择为1 mm×1 mm。有限元模型由3 个部件组成：加载板、支撑板以及波纹管，其中加载板与支撑板为离散刚体，波纹管为壳单元。接触设置为通用接触，摩擦因数取0.3，如图3 所示。

图3 有限元模型

2.3 有限元模型的验证

关于波纹管的试验研究较少，本文根据马闻等[22]的填充波纹管建立了有限元模型并开展仿真，以验证本文模型的有效性。仿真与实验结果吻合良好，如图4和 图5 所示。通过载荷—位移曲线得到耐撞性指标见表2 所示，有限元仿真结果和试验结果误差均不超过5%，因此可以认为本文建立的有限元模型准确可靠。

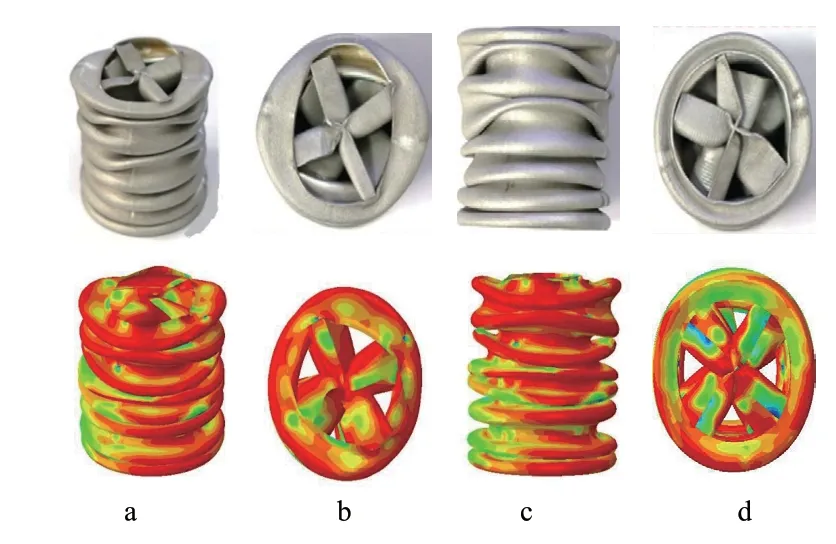
图4 变形模式对比[22]

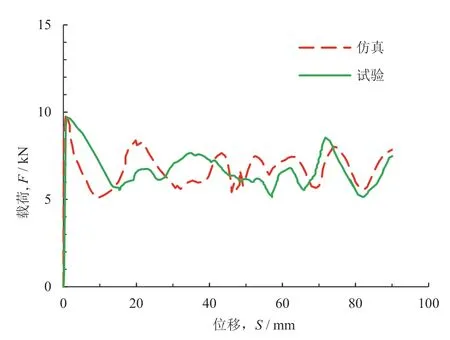
图5 有限元模拟和实验结果的力-位移曲线比较

表2 试验与仿真模型耐撞性参数

3 ECCT 的耐撞性研究

3.1 变形模式

对本文所建立的ECCT 开展准静态单轴压缩仿真，可将ECCT 的变形模式划分为2 大类：非稳定模式(图6)和稳定模式，稳定模式又包括混合模式(图7)、准轴对称模式(图8)和轴对称模式(图9) 3 种。在非稳定模式下，由于波纹幅值和数量较小，应力集中在波纹上，折叠半径与波纹波长不匹配，使得变形不稳定，ECCT 出现不同程度的倾斜。

图6 ECCT 的非稳定变形模式

当ECCT 发生混合变形时，规则褶皱先出现在结构的两端，而后不规则褶皱出现在结构的中部，如图7a 图所示。由于折叠半径与波纹波长较为匹配，2 个分量之间的干扰较小，此时ECCT 并没有出现失稳倾斜的情况，表明增加幅值和波纹数量可以提高ECCT在轴向冲击下的稳定性。当ECCT发生准轴对称变形时，中心轴线会出现弯曲，使得ECCT 的褶皱是倾斜后的轴向对称，如图7b 所示。准轴对称变形模式是由于ECCT 的波纹存在一定的倾角，从而分解冲击力。随着波纹幅值和数量的进一步增多，ECCT 波纹的倾角很小，波纹宽度与折叠半径相匹配，所以变形规则，其变形模式呈现出轴对称变形模式，如图7c 所示。

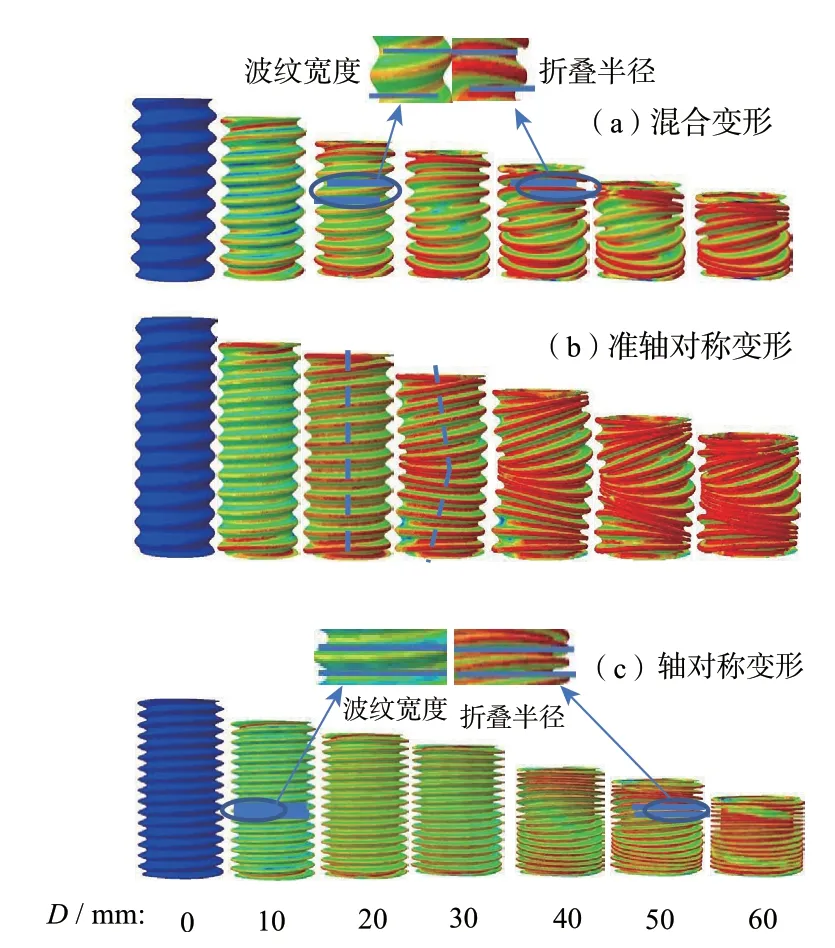
图7 ECCT 的各种变形模式

ECCT 的变形模式统计如图8 所示。由图可知，随着波纹幅值、波纹数量的增加，ECCT 的变形模式越来越规则。当波纹数量小于等于4 或波纹幅值小于等于0.5 mm 时，ECCT 的变形不稳定，其他情况下变形均稳定（除A4N8-ECCT 外）。

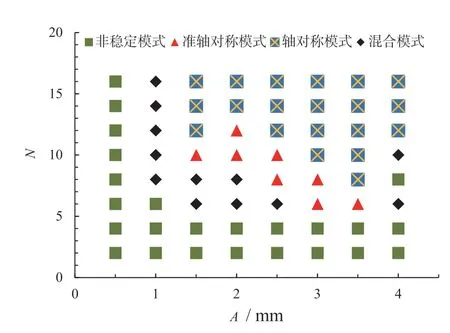
图8 ECCT 变形模式分布图

3.2 载荷-位移曲线

图9 为具有不同结构参数的ECCT 和EDCT 模型，在轴向压缩下其载荷—位移曲线。由图可知，在波纹幅值和数量较小时，曲线震荡明显，且震荡数量通常少于预设的波纹数量，对应的ECCT 都发生了不规则变形。随着波纹幅值和数量的增多，曲线震荡的频率变高，并明显多于预设的波纹数，且震荡的幅值变小，整条曲线更为平滑。特别地，当波纹幅值为4 mm，波纹数量大于等于10 时，ECCT 的载荷—位移曲线可以近似认为是光滑的曲线。对于非稳定变形而言，载荷—位移曲线波动的幅度较大。而且由于变形时发生了不同程度的倾斜，导致曲线的平台段很短，不利于能量吸收，如图9b 中的A4N4-ECCT。

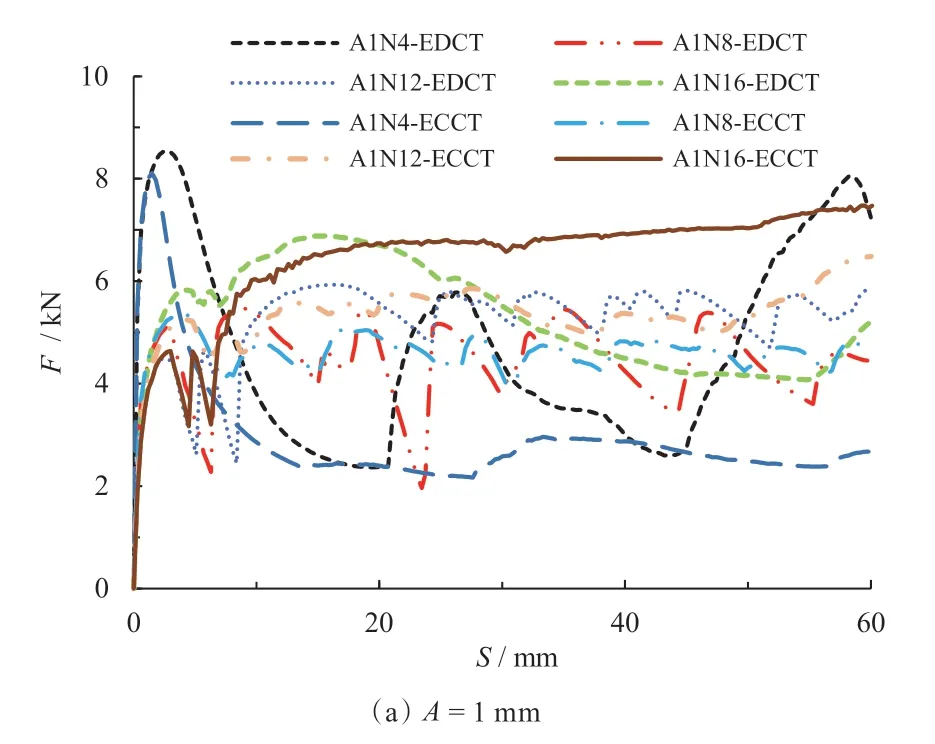
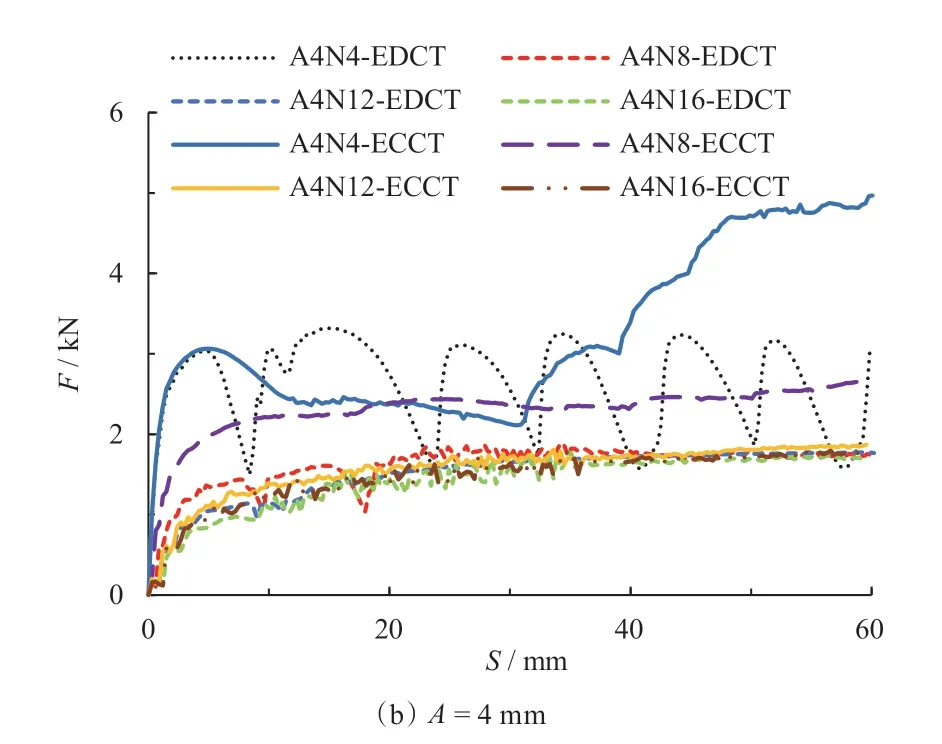
图9 EDCT 与ECCT 的载荷-位移曲线对比

3.3 耐撞性指标

由载荷—位移曲线可以计算ECCT 与EDCT 的各项耐撞性指标，如图10—图15 所示。首先对ECCT 的各项吸能指标进行分析。由图10 可知，ECCT 的IPCF随着波纹幅值和波纹数量的增加，快速下降。当A＞ 2 mm，增加波纹数量可以更显著地降低初始峰值载荷；当A＜ 2 mm，增加波纹幅值可以更显著地降低初始峰值载荷。这是因为波纹幅值和数量较小时，压溃过程接近于圆管，形成塑性铰所需的载荷大，所以初始峰值载荷大。

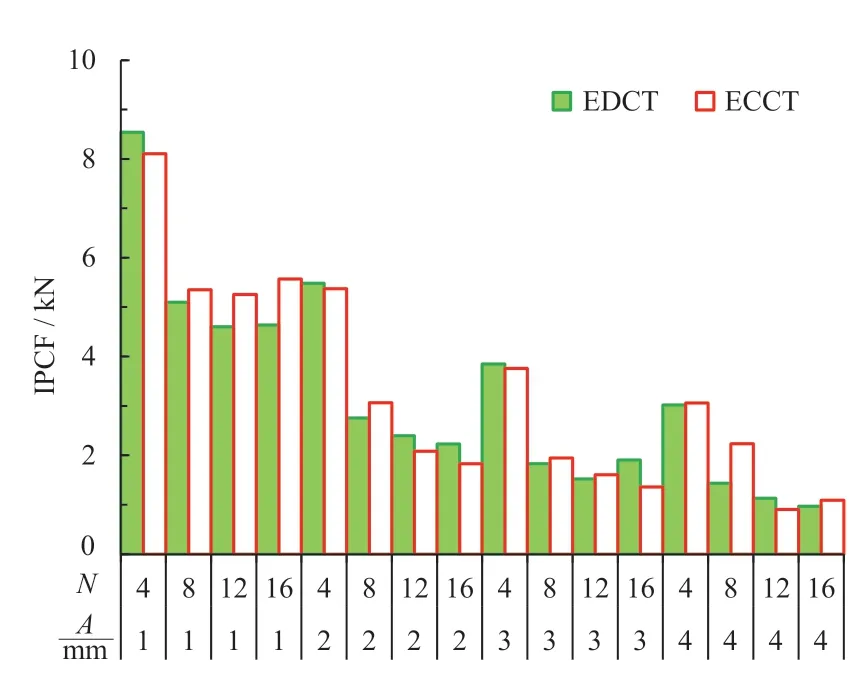
图10 不同参数ECCT 和EDCT 的IPCF

由图11 和图12 可知，随着波纹幅值和波纹数量的增加，ECCT 的EA和SEA 都在减小。这是因为波纹数的增加，改善了其变形模式，使得IPCF 大大降低，从而造成了EA和SEA 的减小。

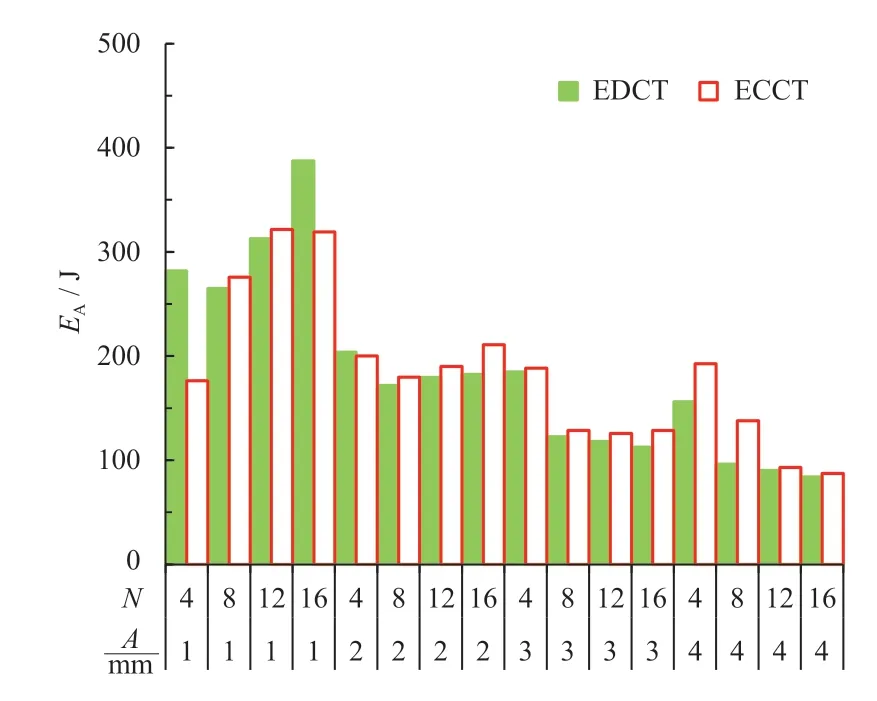
图11 不同参数ECCT 和EDCT 的EA

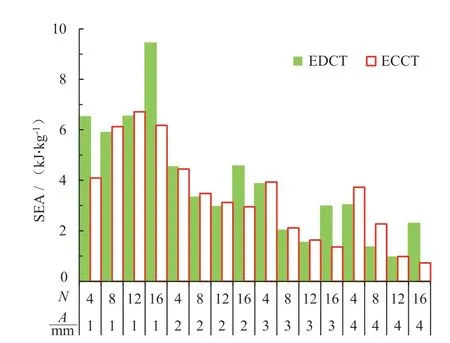
图12 不同参数ECCT 和EDCT 的SEA

由图13 可知，ECCT 的MCF 随着波纹数量和波纹幅值的增加在逐渐变小，其中波纹幅值对MCF 的影响较小，主要原因是波纹数量越多，ECCT 的变形越规则，MCF 越小。例如A4N12（1.550 kN）相比于A2N8（2.995 kN），MCF 降低了约48.3%。但当A=1 mm时，波纹数的增加并没有降低MCF，这是因为A1N4、A1N8-ECCT 出现了失稳现象，失稳后冲击力急剧降低。

图13 不同参数ECCT 和EDCT 的MCF

由图14 可知，ECCT 的CFE 随着波纹数量的增加而增大，随着波纹幅值的增大先增大后减小。由图14可知，ULC 随着波纹数量的增加先减小后增大，当数量等于8 时最小；波纹幅值对ULC 的影响不大。

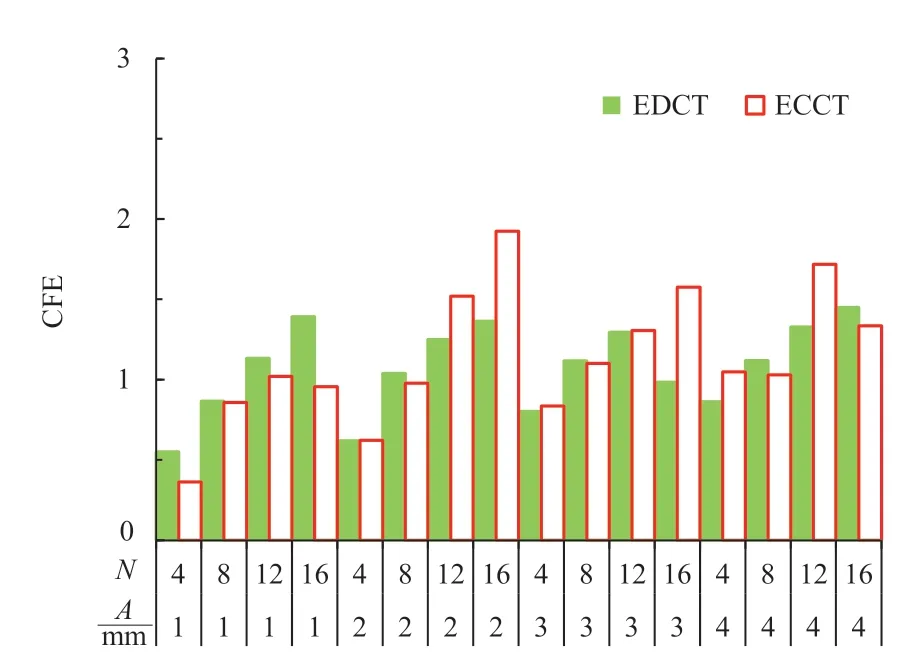
图14 不同参数ECCT 和EDCT 的CFE

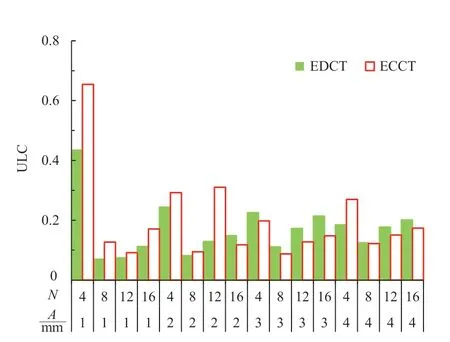
图15 不同参数ECCT 和EDCT 的ULC

进而，开展ECCT 和EDCT 的对比研究。由图10 可知，随着波纹幅值和波纹数量的增加，ECCT 的IPCF 普遍低于EDCT，大大提高了吸能稳定性；由图11 和图12 可知：大部分ECCT 的EA 和SEA 高于同参数的EDCT，表现出良好的吸能效果，但是仍有少数低于EDCT，这是因为此时ECCT 发生了不稳定变形。

由图13—图15 可以发现，ECCT 的MCF、CFE、ULC 略低于EDCT，其主要原因是ECCT 的IPCF 较EDCT 有了大幅度的提高，使MCF、CFE、ULC 的数值降低。综上所述，相同参数下的ECCT 耐撞性要优于EDCT。

3.4 厚度对耐撞性的影响

为了探究壁厚对ECCT 吸能特性和耐撞性的影响，本文选择变形模式为混合变形的A2N8-ECCT 作为研究对象，分别建立H=0.5、1.0、1.5、2.0 mm 4 种厚度的有限元模型，其变形过程如图16。由图16 可知：壁厚越小越容易发生倾斜。当壁厚由0.5 mm 增加到1.5 mm 时，变形模式未发生明显的变化。当壁厚增加到2.0 mm 时，变形模式从混合模式变为准轴对称模式。表明随着厚度的增加变形模式将逐渐改善，主要原因是随着壁厚的增加，ECCT 的应力分布也越来越均匀，从而改善了变形模式。

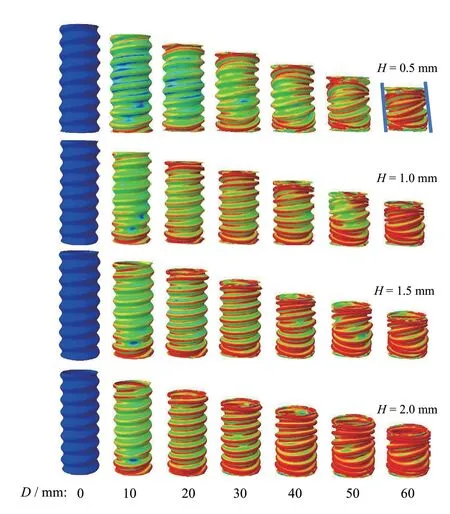
图16 不同厚度A2N8-ECCT 的变形

表3 为不同壁厚A2N8-ECCT 的耐撞性参数。由表可知IPCF、MCF、EA、SEA 会随着壁厚的增加而增大，ULC 会随着壁厚的增加先减小再增大。厚度对CFE 的影响很小，当厚度处于1.0～1.5 mm 之间时，CFE 更接近于1。

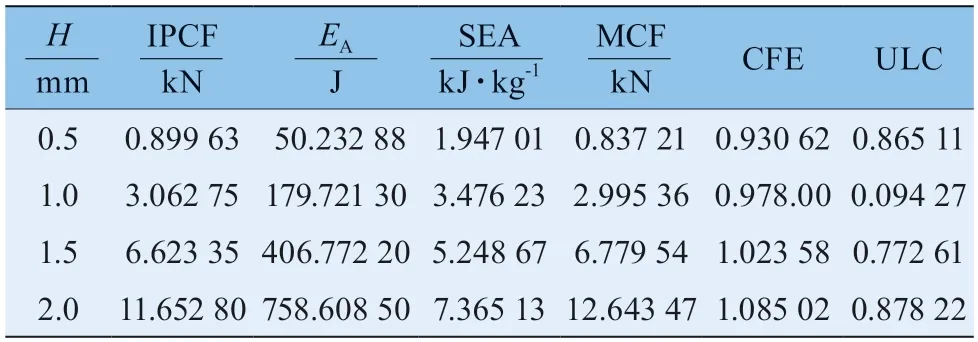
表3 不同厚度A2N8-ECCT 的耐撞性参数

4 多目标优化

4.1 多目标优化数学模型

有限元仿真和试验都只能对有限个模型进行研究，不能确定所设计的结构为最优设计。本文选取波纹幅值A、波纹数量N、壁厚H作为自变量，选取IPCF、SEA 作为目标参数，进行ECCT 的多目标优化以筛选出最佳的设计参数。本文选取的3 个设计变量的取值范围，具体见表4。

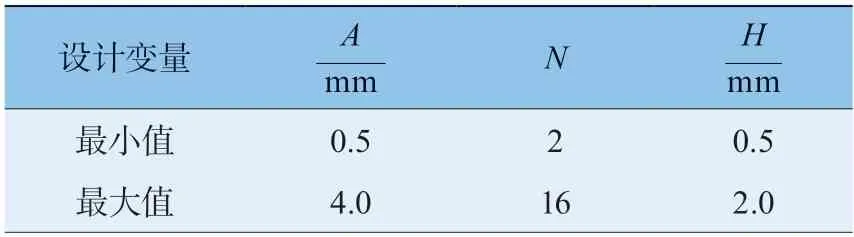
表4 ECCT 优化设计变量

多目标优化的数学模型见式(9)：

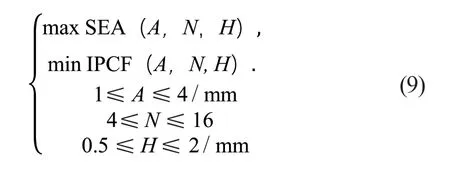
4.2 试验设计

通过试验设计，从样本空间中均匀随机的抽取用于构建代理模型的数据。常用的试验设计方法有正交试验设计、拉丁超立方设计等。当涉及的因素大于等于3，试验工作量大，采用正交试验设计可以实现以最少的试验次数达到与大量全面试验等效的结果。故而本文采用正交试验设计选择了30 组样本。根据样本建立了30 组仿真模型，并得到相关参数，各样本点及相应输出见表5 所示。

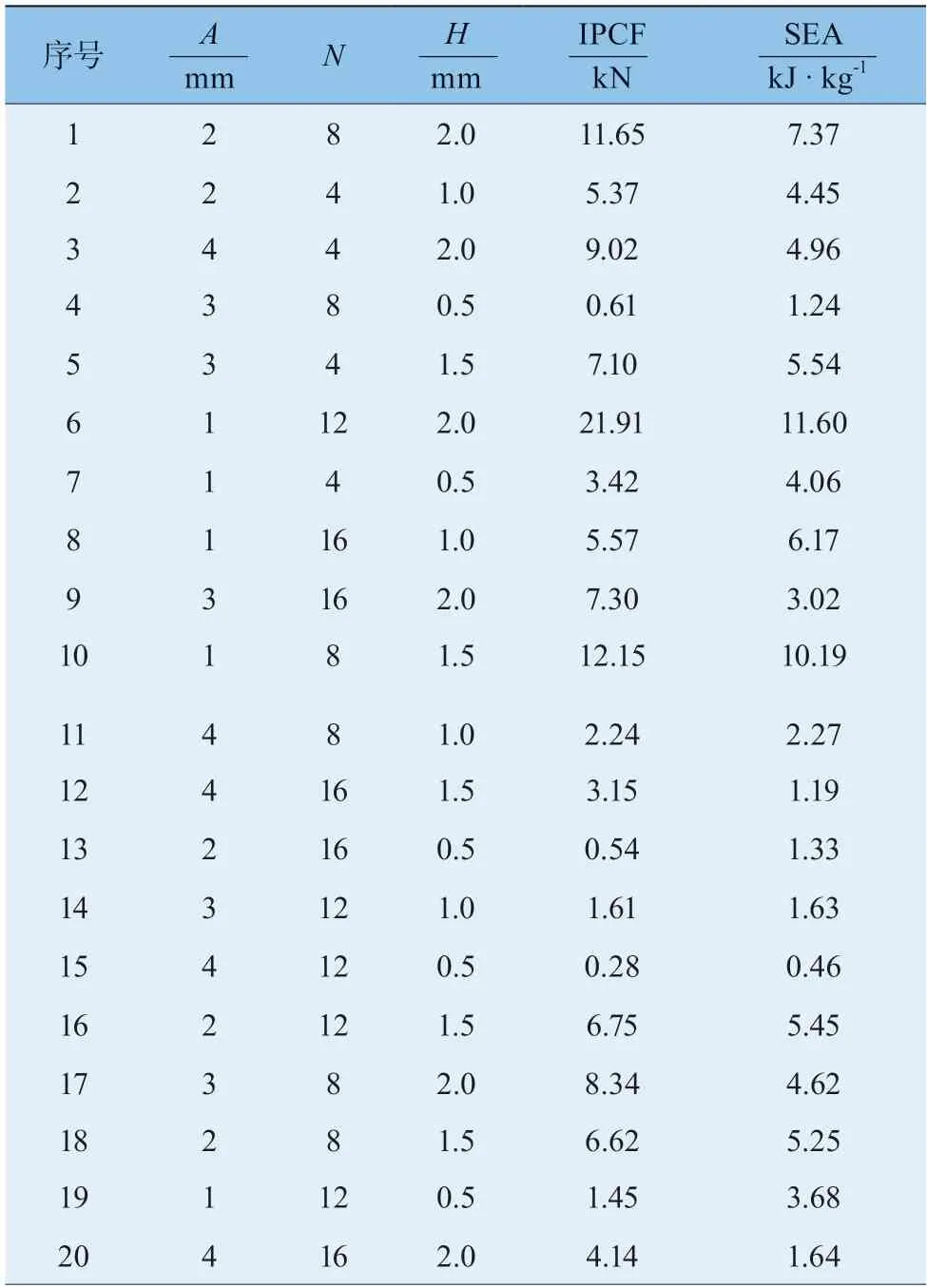
表5 设计变量样本点及相应输出响应

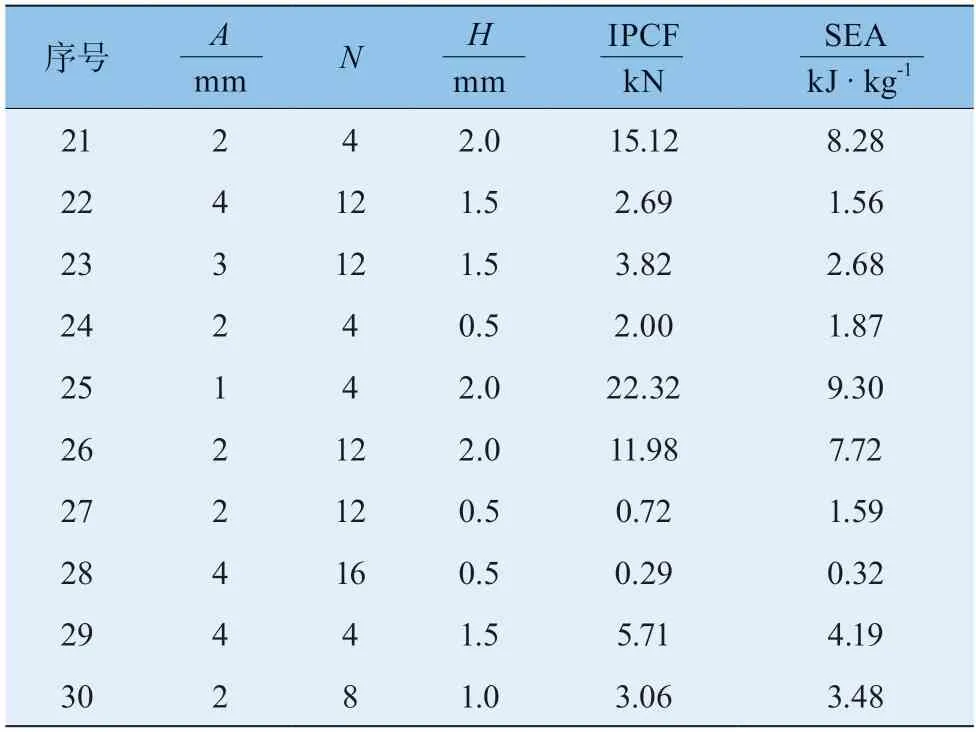
续表

4.3 响应面模型

常用的近似模型有响应面模型、RBF 模型和Kriging 模型等。其中响应面法通过多项式函数来拟合，因近似函数在空间中对应一个曲面，故而得名响应面模型。同时，响应面还具备试验次数少、周期短、精度高等优点。因此，本文选用响应面法拟合近似函数。此外，本文所研究的问题属于相对简单的非线性问题，所以选用二阶多项式函数来进行拟合，如式10。

其中：t是设计变量组成的向量，N是设计变量的数目，αi、αii、αij是待定系数。

将表5 中数据代入上式，即可求出目标参数的二阶多项式拟合函数。求得IPCF 和SEA 的待定系数，见表6。

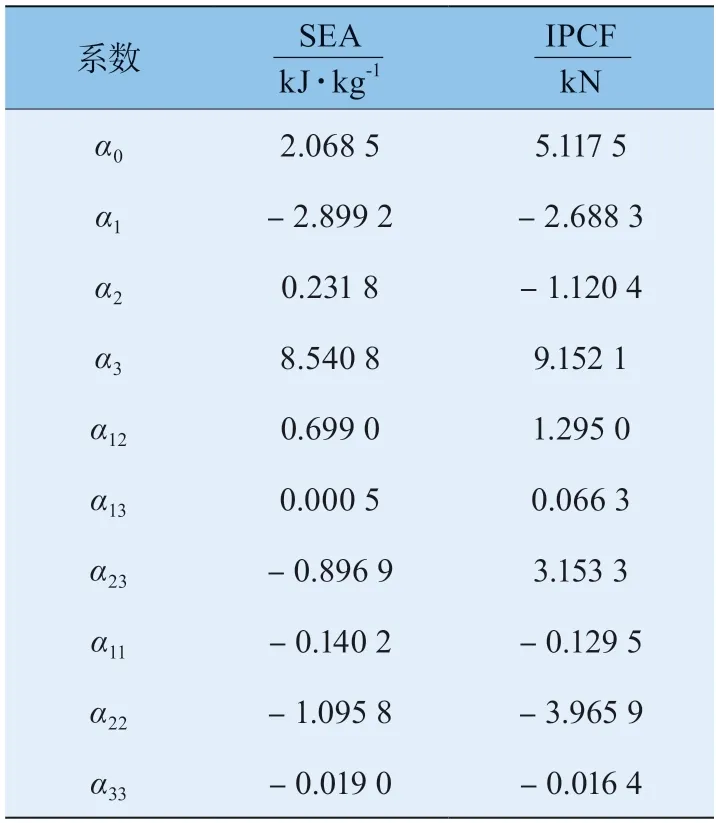
表6 二阶多项式响应面模型的系数

得到相应的响应面函数之后，还需要对其准确性进行检验。R2是用于评价响应面函数对样本点数据拟合精度的指标，其越接近1，表明误差越小，拟合函数精度越高。本文选用R2作为响应面模型精度的评价指标，即：

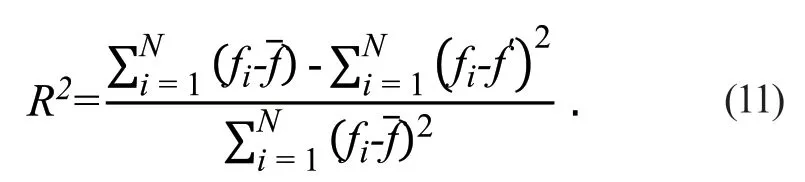
一般而言，R2＞ 0.9 即可认为响应面模型满足要求。由式(11)可得到SEA 和IPCF 的R2计算值分别为0.9733 和0.9752，可知响应面模型满足精度需求。

为了进一步验证响应面模型的精度，在样本空间中随机抽取2 个点(点I：A=0.5 mm,N=4,H=0.5 mm;点II：A=0.5 mm,N=4,H=0.5 mm)进行验证,其预测值与仿真结果对比见表7 所示，可以得出各样本响应值(α)与预测值(β)的相对误差(E)均小于10%，证明响应面模型满足精度要求。

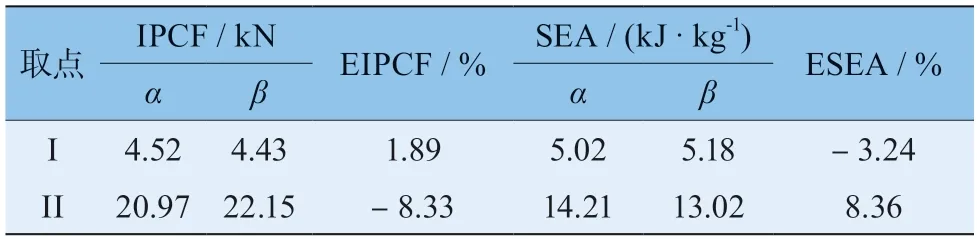
表7 随机抽样样本点响应值与预测值对比

4.4 优化结果

本文选用由Srinivas 和 Deb 在NSGA 基础上改进的NSGA-Ⅱ 算法[23]，其优点在于采用了快速非支配排序算法，大大降低了计算的复杂性，使Pareto 解集更为均匀，提高了算法的运算速度和鲁棒性。本文的Pareto 解集如图17 所示。根据实际需求在Pareto解集中选取的优化结果A=0.500 mm、N=15.927、H=1.383 mm。为了制造方便，将参数圆整为A=0.5 mm、N=16、H=1.38 mm，并以这组参数建立有限元模型以验证优化结果的准确性，两者结果对比见表8。

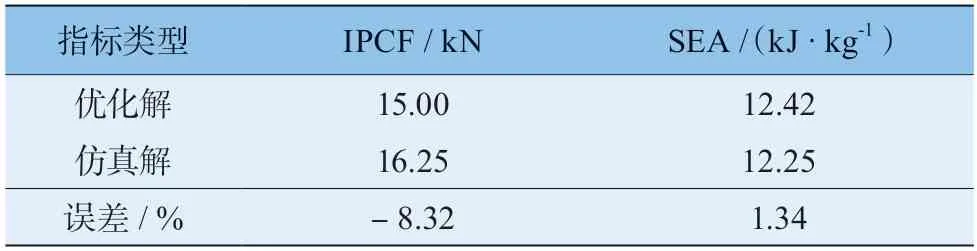
表8 优化得到的性能参数与仿真计算结果对比

图17 ECCT 多目标优化的Pareto 前沿解集

由表8 可得，有限元仿真结果与优化结果相比误差不超过10%，证明本文优化结果可靠。同时对比相同参数的ECCT 与EDCT，SEA 基本保持不变，IPCF降低了14.31%，见表9，表明本文所提出的新型波纹薄壁结构是一种高效吸能结构。

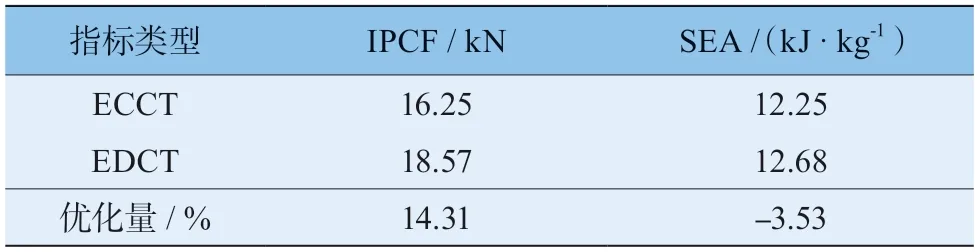
表9 相同优化参数的ECCT 与EDCT 对比

5 结论

本文提出并建立了新型连续波纹结构铝合金吸能盒，研究了在单轴压缩下，波纹结构参数对其变形模式和耐撞性的影响，最后开展了基于吸能盒耐撞性的多目标优化设计，得到如下结论：

1）当波纹幅值、波纹数量相等时，等距连续波纹管的初始峰值载荷、比吸能等性能指标均优于等距离散波纹管。

2）单轴压缩下，当波纹数量≥8 时，等距连续波纹管发生稳定变形，其变形模式可以分为3 种：混合模式、准轴对称模式、轴对称模式。

3）选取等距连续波纹管的波纹幅值、波纹数量和壁厚作为优化参数，初始峰值载荷和比吸能作为优化目标进行多目标优化。优化后，初始峰值载荷降低了14.31%，比吸能降低了3.53%。