小倾角LEO多星天基平台光学跟踪GEO精密定轨*

邵 瑞 宋叶志 叶 钊 曾春平 胡小工

(1 中国科学院上海天文台上海200030)

(2 中国科学院大学北京100049)

(3 航天东方红卫星有限公司北京100094)

1 引言

随着航天技术的飞速发展, 越来越多的空间目标进入太空, 人造卫星作为主要的空间目标在诸多领域发挥了不可替代的作用. 然而在人类进行空间活动的同时, 也产生了数量庞大的空间碎片. 这些空间碎片逐渐成为威胁航天资源的主要原因, 至今已发生了多次空间碰撞事件[1]. 面对日渐严峻的空间环境, 对空间目标的追踪、监测和精密定轨, 实现对其进行全面编目和管理显得尤为重要.

地球同步轨道目标由于其独特的轨道特性, 在通信、侦查、中继等领域发挥着重要的作用, 这也使得对地球静止轨道(Geostationary Earth Orbit, GEO)目标追踪观测提出了更高的要求[2]. 通过对GEO卫星的跟踪, 可以对其运行状态进行评估, 以达到预测恶意攻击和碰撞规避的目的. 现阶段对于GEO卫星所采用的主要监视手段按照观测方式主要分为天基和地基观测[3]. 传统的地基观测手段在观测过程中会受到空间介质的影响, 在测站分布上会受到政治因素的限制, 很难对境外GEO卫星进行跟踪测量, 而在一些航天任务中对GEO卫星监测的定轨精度与时效性都有一定的要求, 因此地基测控网往往较难满足相应的需求. 在以往的研究中, 黄勇等人利用VLBI (Very Long Baseline Interferometer)测轨数据以及C波段转发式测距数据对GEO卫星进行定轨分析, VLBI时延测量精度为3.6 ns, 定轨精度可达到10 m左右的量级[4]; 宋叶志等人利用多台站双频双程测距模式, 对风云四号卫星进行动力学轨道确定, 在非变轨期间精度优于20 m, 动量卸载期间, 采用估计经验力的方法, 定轨残差优于1 m[5]; 刘凯等人基于一发多收的转发模式对GEO卫星进行定轨, 结果精度可达到10 m[6]; 于涌等人利用地基单站CCD (Charge Coupled Device)漂移扫描光电技术, 对同步轨道目标进行测定轨, 在多圈观测的情况下, 定轨精度优于50 m[7].

天基空间目标监测常用的手段有光学、红外以及雷达3种, 其中红外探测作用距离短, 雷达探测的技术难度较大, 光学技术相比前两种技术更为成熟, 因此可以更好地运用于天基监测. 较之于地基测控技术, 天基光学探测具有功耗更小、作用距离远、观测不受位置和天气的影响等特点, 同样口径的望远镜, 探测能力比地基更强, 没有背景天光的影响, 因此天基探测未来会成为空间目标监测的一个重要的发展方向. 国外在天基光学监测投入了大量的科研精力, 取得了丰厚的研究成果. 美国自上世纪90年代起开始在卫星上安装SBV (Space-Based Visible)相机, 并在之后对卫星进行更新换代, 提升对空间目标, 尤其是GEO卫星的监测能力[8–11]. 欧空局(European Space Agency, ESA)Flohrer等人对低轨平台监测GEO卫星的可行性进行了研究和论证[12]. 将天基光学测角资料用于卫星轨道确定的研究在国内较少. 李冬等人在文献[13–14]中, 利用两个短弧段的天基测角资料实现了对GEO卫星空间目标的轨道确定.

本文基于小倾角低地球轨道(Low Earth Orbit, LEO)多星组网天基平台, 利用光学跟踪GEO卫星对其进行精密定轨, 平台的轨道通过其他途径获取. 首先对平台和目标进行光学的可视性分析,介绍星载CCD天文定位的原理, 进而给出利用光学测角资料进行轨道确定的方法, 最后对系统进行仿真, 对算法进行验证分析.

2 天基平台的空间目标可视性分析

光学CCD相机在对空间目标进行观测时, 会受到诸多空间环境的限制, 同时也会受到自身照相设备硬件条件的限制, 在仿真过程中需要考虑相机作用距离的影响, 根据平台和目标的相对位置即可解算两者之间的距离, 根据距离阈值进行筛选; 还需考虑地球遮挡与地光条件、地影条件以及太阳光影响[15–16]; 此外平台载荷的扫描区域由载荷的视场决定, 本次仿真采用的视场类型为带状视场, 设相机视场角度为θ1、θ2, 其中θ1张角垂直于平台轨道面,θ2位于轨道平面内, 只有同时满足两个条件,空间目标才能出现在星载相机的视场内.

首先判断目标是否出现在垂直轨道面的θ1/2的视场内, 天基平台所在轨道面的法向量为:

其中hs为平台轨道的法向量,rs为平台的单位位置矢量,vs为平台的单位速度矢量, 本文所有矢量皆在地心天球坐标系下描述. 空间目标到天基平台的位矢与天基平台轨道面法向量之间的夹角为

其中robj为目标的单位位置矢量, 空间目标到天基平台的位矢与天基平台轨道面之间的夹角为:

当|λ2|≤θ1/2, 满足空间目标出现在垂直轨道面的视场内.

使用的球面三角法判断空间目标是否出现在轨道平面内的视场, 球面三角法的原理如图1所示.

图1左侧是地心、平台、目标以及目标在平台轨道面投影的空间图, 右侧是平台、目标以及目标投影在天球上构成的球面三角.O为地球质心,为平台位置的单位矢量,为目标位置的单位矢量,在平台轨道面内的投影. 由于∠BOA为α, 则弧为α; ∠COB为β, 则弧为β; ∠AOC为γ, 则弧为γ, 在球面三角中∠BAC为90°. 利用球面三角解法可得当|γ|≤θ2/2, 满足空间目标出现在位于轨道面的 视场内.

图1 球面三角法求解示意图Fig.1 Schematic diagram of spherical trigonometry

3 天基光学测角轨道改进方法

3.1 观测量类型及其观测方程

CCD是一种广泛运用于照相天体测量的光电转换固体器件, 常用于一些大型望远镜和星载光学设备上, 对红外光和可见光十分灵敏, 具有成像几乎无畸变、像素稳定等优点. 利用CCD成像中的空间目标和背景恒星的相对位置, 通过计算其理想坐标, 得到其赤经和赤纬.

大气折射主要发生在40 km以下的高度, 而本文的仿真平台和目标所处高度皆高于此, 因此大气折射对观测的影响基本可以忽略. 由于光线传播到卫星需要一定的时间, 在光线传播的同时, 平台卫星与目标卫星都处于运动状态, 需要进行光行时改正.

利用修正后的观测量, 建立如下观测方程:

其中μ、δ分别为赤经和赤纬, (x,y,z)、(xs,ys,zs)分别为目标卫星和观测平台在天球参考系下的坐标分量.

3.2 统计定轨批处理方法

对于静止卫星的轨道计算所采用的策略以及动力学方法如表1所示, 其中ITRS为国际地球参考系(International Terrestrial Reference Frame);IAU为国际天文学联合会(International Astronomical Union); JGM为联合引力模型; DE表示Development Ephemeris, 是美国喷气推进实验室推出的系列星历; RTN表示轨道坐标系; QR表示正交三角; KSG为积分器发明人Krogh Shampine Gordon的缩写; POD为精密定轨(Precise Orbit Determination).

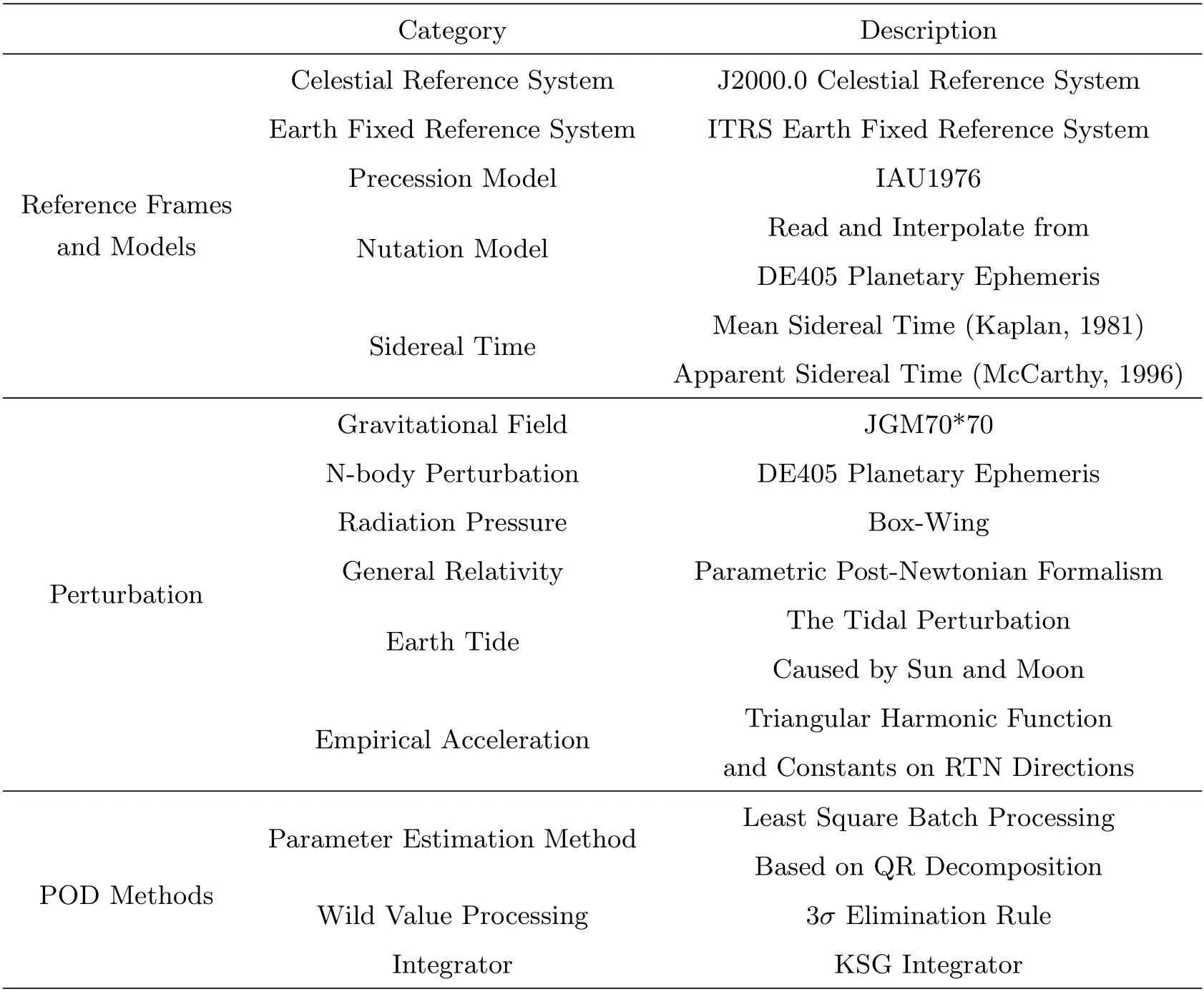
表1 摄动力以及定轨策略Table 1 Perturbations and strategies of orbit determination

设在tj时刻有一组观测量Yj，j为某个时刻下标:

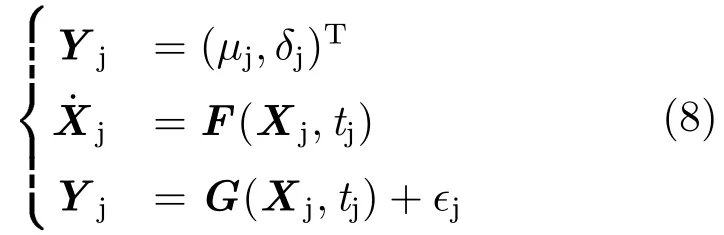
其 中μj,δj为tj时 刻 赤 经 赤 纬 观 测 量，Xj=(rp)是空间目标在tj时刻的状态矢量，r为空间目标的位置矢量，˙r为空间目标的速度矢量，p为待估参数，包括大气阻力系数、太阳光压系数等。F(Xj,tj)是和状态量相关的力学参数以及速度等。G(Xj,tj)是tj时刻观测量的真值，ϵj为测量误差。假设某一时刻参考状态为X*，将动力系统在X*线性化展开并略去二次以上高阶项整理可得：

其中O为观测值，C为理论值，X0是待估状态量，ΔX为待估状态量的改正值。为测量矩阵，具体表达形式可参考Tapley等[17]在书中的描述，采用数值解时，可以把对轨道动力学方程和状态转移矩阵的微分方程同步积分。

卫星精密定轨的工作是采样大量观测数据Y j求解条件方程, 给出待估状态量的改正值,从而得到改进的历元状态量. 其过程是一个迭代过程, 将每次得到的改进历元状态量作为估计量重复前面的过程, 直至满足精度为止.

4 定轨仿真校验

仿真算例中LEO组网的轨道为小倾角轨道, 轨道面和GEO卫星轨道面几乎重合, 组网轨道的高度为900 km, 测角精度分别为5′′和3′′, 轨道平台3个方向的振幅为5 m, 数据采样率为3 s. 每个平台星载CCD相机的视场角为16°×2°, 镜头指向沿径向背离地心.

4.1 双星LEO组网对GEO卫星进行轨道跟踪测定

定轨弧段为(UTC, 协调世界时): 2020年10月22日4点至2020年10月22日16点, 下文各个结果分析图的横坐标时间对应的年、月、日为2020年10月22日, 在图中省去.

初始历元(2020年10月22日4时)两颗LEO平台和GEO卫星的初轨信息如表2所示, 其中a为轨道半长轴、e为轨道离心率、i为轨道倾角、ω为近地点幅角、Ω为升交点赤经、M为平近地点角.

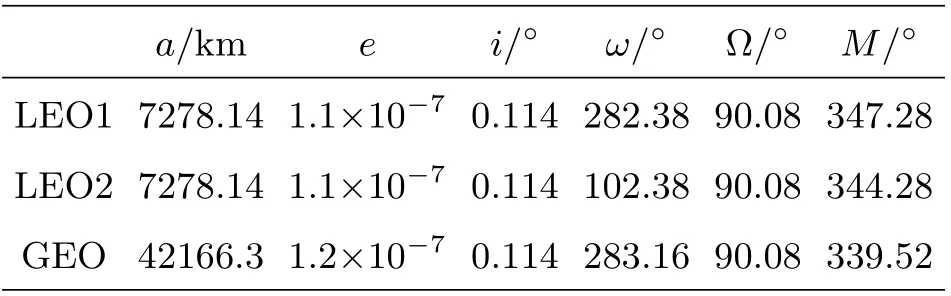
表2 双星LEO平台与GEO卫星初始星历Table 2 Initial ephemeris of two LEOs and GEO

根据仿真条件生成仿真数据, 利用仿真数据进行定轨, 在测角精度为5′′的情况下, 12 h弧段台站1和台站2的观测残差如图2所示, 图2上半部分为台站1、2观测数据的赤经残差, 右上角1、2为台站序号. 下半部分为观测数据的赤纬残差, 横坐标是观测时间(UTC协调世界时), 纵坐标是残差范围(后续残差图介绍定义同理).

图2 12 h观测的台站1、2定轨残差Fig.2 POD residuals of stations 1, 2 with 12 h observation

由图2可以看出, 残差与仿真噪声大体相等. 图3给出了两颗小倾角LEO平台对GEO卫星跟踪定轨结果和仿真轨道在RTN轨道坐标系下的比较结果, R为径向, T为迹向, N 为轨道面法向. 图3上半部分为位置的偏差, 下半部分为速度的偏差, 横轴为观测时间, 纵轴为偏差范围. 轨道精度大致在千米量级(RMS, 均方根偏差, 后续轨道重叠精度图介绍定义同理). 在测角精度为3′′的情况下, 定轨结果和仿真轨道的对比如图4所示, 轨道精度大约为800 m左右.

图3 双星LEO对GEO卫星定轨与仿真轨道比较Fig.3 Overlap of GEO POD by two LEOs and simulation orbit

图4 当测角精度为3′′时, 双星LEO对GEO卫星的定轨结果与仿真轨道的比较Fig.4 Overlap of GEO POD by two LEOs and simulation orbit under the condition of 3-arcsecond measurement accuracy

4.2 3星LEO组网对GEO卫星进行轨道跟踪测定

定轨弧段同双星LEO组网, 初始历元3颗LEO平台和GEO卫星的初轨信息如表3所示.

表3 3星LEO平台与GEO卫星初始星历Table 3 Initial ephemeris of three LEOs and GEO

根据仿真条件生成仿真数据, 利用仿真数据进行定轨, 在测角精度为5′′的情况下, 12 h弧段台站1、台站2和台站3的观测残差如图5所示.

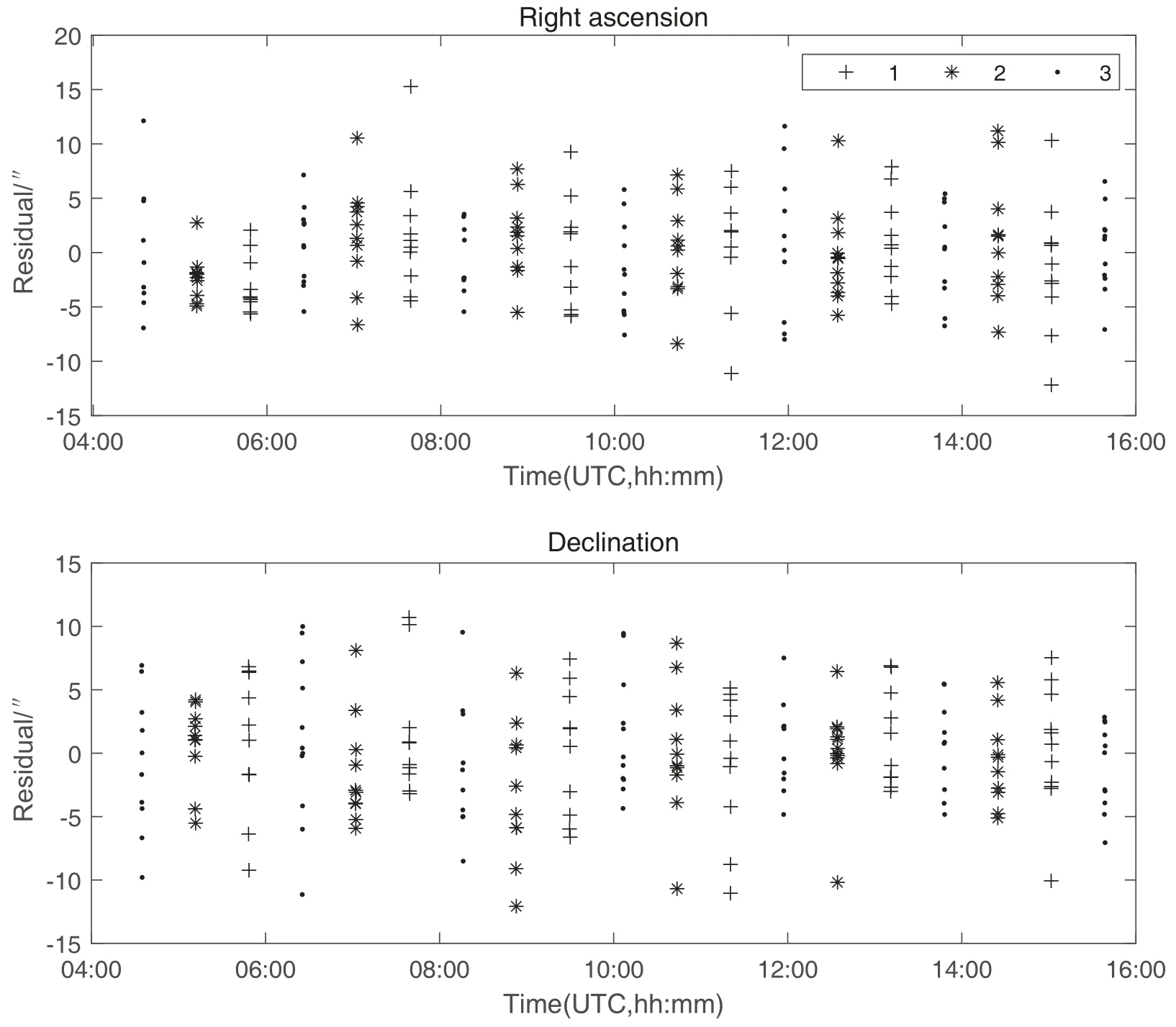
图5 12 h观测的台站1、2、3定轨残差Fig.5 POD residuals of stations 1, 2, 3 with 12 h observation

图6给出了3颗小倾角LEO平台对GEO卫星跟踪定轨结果和仿真轨道在RTN轨道坐标系下的比较结果. 由图6可以看出, 定轨精度大约在600 m量级. 在测角精度为3′′的情况下, 定轨结果和仿真轨道的对比如图7所示, 此时轨道精度大约为350 m左右.

图6 3星LEO对GEO卫星定轨与仿真轨道比较Fig.6 Overlap of GEO POD by three LEOs and simulation orbit

图7 当测角精度为3′′时, 3星LEO对GEO卫星的定轨结果与仿真轨道的比较Fig.7 Overlap of GEO POD by three LEOs and simulation orbit under the condition of 3-arcsecond measurement accuracy

4.3 4星LEO组网对GEO卫星进行轨道跟踪测定

定轨弧段同双星LEO组网, 初始历元4颗LEO平台和GEO卫星的初轨信息如表4所示.

表4 4星LEO平台与GEO卫星初始星历Table 4 Initial ephemeris of four LEOs and GEO

根据仿真条件生成仿真数据, 利用仿真数据进行定轨, 在测角精度为5′′的情况下, 12 h弧段台站1、台站2、台站3和台站4的观测残差如图8所示.

图8 12 h观测的台站1、2、3、4定轨残差Fig.8 POD residuals of stations 1, 2, 3, 4 with 12 h observation

图9是4颗小倾角LEO平台对同一个GEO卫星跟踪定轨结果与仿真轨道在RTN坐标系下的比较,由图9可以看出, 精度大约在百米量级以内. 在测角精度为3′′的情况下, 定轨结果和仿真轨道的对比如图10所示, 轨道精度大约为50 m左右.

图9 4星LEO对GEO卫星定轨与仿真轨道比较Fig.9 Overlap of GEO POD by four LEOs and simulation orbit

图10 当测角精度为3′′时, 4星LEO对GEO卫星的定轨结果与仿真轨道的比较Fig.10 Overlap of POD GEO by four LEOs and simulation orbit under the condition of 3-arcsecond measurement accuracy

通过对以上3个仿真算例的结果进行分析可以看出各个台站的残差水平接近仿真噪声. 轨道重叠图中的位置和速度差异主要体现在R方向上, 这主要是由观测资料的类型造成. 本文使用的观测资料是天文定位的结果, 属于角度观测量, 对R方向的约束较弱, 因此R方向偏差较大. 随着观测平台数量的增加, 由于从不同方向对目标进行测量, 因此空间几何结构有一定变化, 在数目较多时, R方向的误差不一定总是最大. 另外在仿真过程中也会受到其他诸如组网和目标的初始位置构型等因素影响, 因此会在结果上产生一定差异.

本文还对5颗和6颗的平台组网对GEO卫星定轨进行了仿真. 在相同的定轨时长下, 5颗组网, 观测精度5′′, 定轨精度为59.0368 m; 观测精度3′′, 定轨精度为35.0557 m. 6颗组网, 观测精度5′′, 定轨精度为54.0379 m; 观测精度3′′, 定轨精度为30.0036 m. 各数量平台在不同测角噪声下的定轨精度如表5所示.

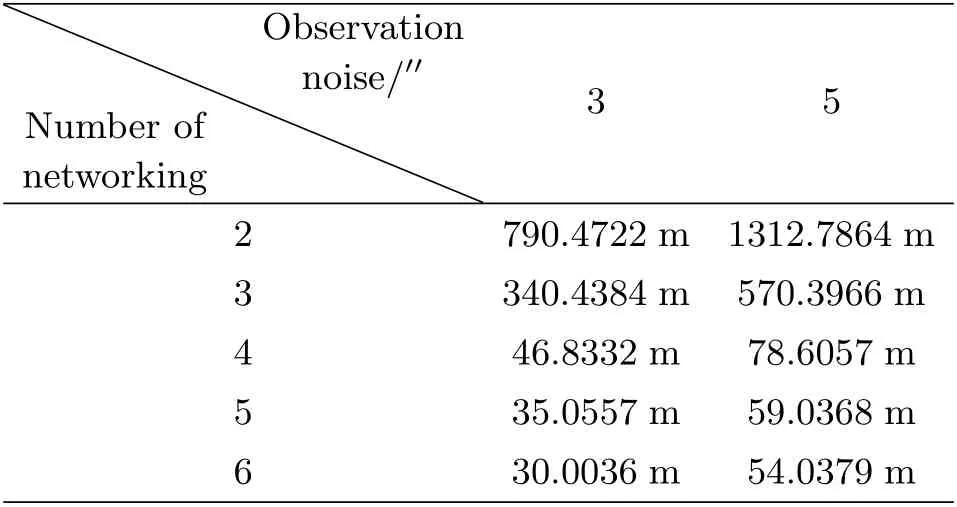
表5 定轨结果统计Table 5 POD results statistics

5 总结

本文对星载CCD相机跟踪观测空间目标进行模拟. 通过光学可视性分析, 对模拟的观测数据进行筛选, 利用筛选得到的数据, 采用数值方法进行空间目标的轨道确定. 平台皆为小倾角的LEO卫星, 采用不同数量的LEO平台组网, 在不同测量精度下定轨, 得到的结论如下:

(1)对于同一测量精度(5′′)而言, 在平台数量较少的情况下, 两颗LEO平台组网定轨12 h, 轨道精度大约是千米量级; 3颗LEO平台组网定轨12 h, 轨道精度约为600 m; 4颗LEO平台组网定轨12 h, 轨道精度在百米以内. 在组网数量少的情况下, 定轨精度随着组网数量的增加得到了较大的提升, 验证了多星组网天基光学定轨的可行性. 在平台数量累计到5星组网的情况下, 相同定轨条件下定轨精度为59.0368 m; 6星组网的情况下, 定轨精度为54.0379 m, 随着组网中平台数量的增加, 精度的提升幅度逐渐减小;

(2)当LEO平台组网中平台数目一定时, 测量精度对定轨精度的影响较大, 测量精度从5′′提升至3′′, 定轨精度也相应提升了近一倍. 验证了通过提升测量精度来提升定轨性能的可行性. 在实际工程中, 平台的轨道可以通过地面测控站或者星载GNSS接收机进行观测获取, 两种技术已经相对成熟, 且精度较高. 地基CCD观测虽然具有低成本、操作简单等有优势, 但是在对GEO卫星进行观测时, 由于GEO卫星相对地面不动, 因此会造成测站与目标之间的几何构型变化甚微, 而LEO星载平台可以很好地解决这个问题. 在未来, LEO星载平台在卫星测控领域可能会有很好的应用前景.