基于深度学习的LAMOST星系星族参数测量*
王丽丽 张龙威 杨光军 张俊亮 刘 聪
(1 德州学院计算机与信息学院德州253023)
(2 德州学院能源与机械学院德州253023)
1 引言
星系是一个由恒星、气体和尘埃等物质共同构成的巨大系统. 一条星系的光谱是由千亿颗恒星的累积光而形成的, 记录了星系成员星的年龄和金属丰度等相关信息, 对星系的各种物理参数进行分析, 可以推导星系的恒星形成历史和物理化学演化历史. 推导星系中的星族成分主要有3大类方法: 基于线指数的方法、星族合成方法和机器学习或深度学习方法.
基于线指数的星族成分分析方法使用了特定谱线的强度或等值宽度,例如Lick指数[1].根据线指数对年龄或金属丰度的敏感性[2], 我们可以使用线指数示踪某元素的丰度, 也可以度量平均年龄和金属丰度. 这种方法的优势是对消光或流量定标不敏感, 而且可以打破星族成分的简并. 然而, 线指数只使用了整个观测光谱范围之内的几个特征谱线, 而且由于星系光谱运动学致宽且光谱分辨率不够高,很多谱线会混杂在一起不易分辨, 给测量增加了难度. 使用光谱数据测量星族年龄和金属丰度最常用的方法是星族合成方法, 其基本思想是将光谱模板与待测光谱进行拟合来推导星系的星族成分, 这种方法使用了光谱上尽可能多的信息. 使用全谱进行模板匹配的算法层出不穷, 例如STARLIGHT[3]、PPXF[4](penalized pixel-fitting)和FIREFLY[5](Fitting IteRativEly For Likelihood analYsis)等.这些算法的研究对象是光谱的积分特征, 所以依赖于待测光谱和模板光谱的连续谱形状. 如果光谱的流量定标不准确, 使用模板匹配方法得到的星族参数值可能存在较大的不确定性.
随着大规模巡天工程的开展, 天文数据呈现一种爆炸性的增长. 面对如此海量、高维的天文数据, 基于机器学习、数据挖掘等方法为数据的处理和分析提供了有效思路和途径. 机器学习或深度学习技术广泛应用于星系或恒星参数的测量[6–9]. 基于机器学习或深度学习的参数测量方法的基本原理是使用具有已知物理参数的训练样本, 生成统计模型来预测这些参数在目标数据集中的分布. 例如文献[6]使用星系的红移、光度和颜色数据利用随机森林算法估计星系的恒星质量和恒星形成率, 文献[7–8]构建了一个栈式自编码深度神经网络, 测量Sloan Digital Sky Survey (SDSS)的恒星大气物理参数, 并与神经网络、支持向量机等算法比较, 结果表明深度神经网络预测精度更高, 文献[9]使用深度神经网络和强化学习测量星系和暗物质晕的物理参数. 但是基于深度学习技术使用光谱数据测量星系年龄和金属丰度的文献比较少.
LAMOST (Large Sky Area Multi-Object Fiber Spectroscopic Telescope)[10–11]是我国研制的一种大型光学望远镜. 截至2020年6月, 包含先导巡天及正式巡天7 yr的LAMOST Data Release 7(DR7)数据集向国内研究人员及国际合作者发布, 共发布光谱10640255条, 其中包括恒星光谱9881260条、星系光谱198393条、类星体66406条、未知天体光谱494196条. 使用LAMOST星系数据,研究人员进行了星系对[12]、双峰发射线星系[13]等方面的研究. 另外, 有文献测量了LAMOST星系的星云发射线[14]和速度弥散[15], 并发布相应的增值星表. LAMOST星系的星族成分测量方面的相关研究较少, 主要困难在于LAMOST光谱的流量没有得到很好的校准. LAMOST巡天中光谱数据处理采用相对流量定标方法, 因选用标准星的红化具有一定的不确定性, 进而在流量定标时影响了光谱连续谱形状[14]. 传统的星族合成方法测量星族参数时依赖于待测光谱和模板光谱的连续谱形状. 所以如果使用星族合成方法推导LAMOST星系光谱的星族成分, 得到的结果可能会存在较大的误差. 在我们前期工作中[16], 提出了一种基于小尺度特征的模板匹配方法对LAMOST星系估计平均年龄和金属丰度, 误差在0.2 dex左右. 该方法将LAMOST光谱的连续谱从全谱中扣除后, 使用小尺度特征(主要是吸收线特征)与模板谱进行非线性拟合来推导星族参数. 这种方法使LAMOST星系星族参数测量不受连续谱的影响, 但模板匹配过程中采用非线性拟合方法, 计算量较大, 时间复杂度比较高.
本文结合LAMOST星系光谱特点和深度学习方法的优势, 提出的参数估计方法使用卷积神经网络构建回归模型, 推导LAMOST星系的年龄和金属丰度, 实现参数的自动估计. 该方法直接使用LAMOST星系光谱的全谱信息进行有监督的深度学习, 不需要对光谱连续谱进行处理来避免流量定标导致的连续谱不准确问题, 具有很好的应用价值.
2 方法
我们提出的LAMOST星系星族参数自动估计的工作流程如图1所示.
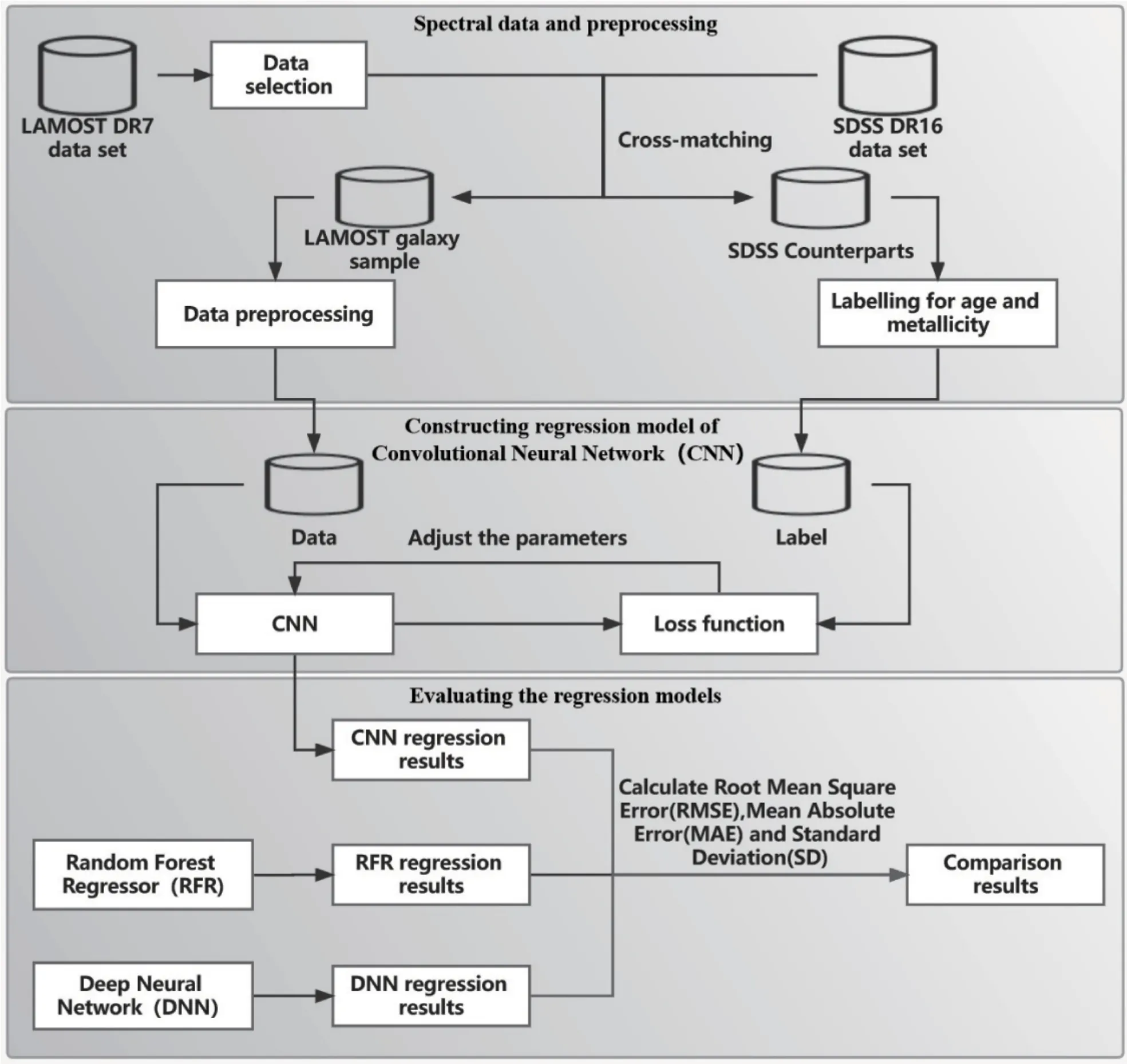
图1 LAMOST星系星族参数估计的工作流程Fig.1 Framework of estimating stellar population parameters for LAMOST galaxies
(1) LAMOST数据筛选与数据预处理. 首先,我们从LAMOST DR7中选择星系光谱作为研究对象, 挑选满足一定信噪比和红移条件的光谱. 将筛选得到的LAMOST星系光谱与SDSS Data Release 16 (DR16)发布的光谱数据(大家公认其连续谱比较准确)进行交叉, 用SDSS同源光谱的年龄和金属丰度来标记深度学习中LAMOST光谱真实参数值.对于LAMOST星系样本光谱进行退红移和重采样,作为输入送入卷积神经网络中, 对于使用SDSS同源光谱得到的年龄和金属丰度作为标签送入网络中;
(2)卷积神经网络回归模型的构建与训练. 构建卷积神经网络对步骤(1)中得到的LAMOST星系样本及其标签进行训练;
(3)卷积神经网络回归模型的评估与对比. 使用均方根误差、平均绝对误差和标准差等评价指标来衡量卷积神经网络的预测效果. 另外, 将该网络模型与随机森林回归模型和深度神经网络进行对比评价.
2.1 数据筛选与预处理
LAMOST DR7中包括星系光谱约19万条, 首先按照条件: r波段信噪比S/Nr≥5并且红移z <0.3筛选光谱数据, 这样可以提高分析样本的质量,并且保证主要谱线特征([OIII]λ5007、Hβ、Hα、[NII]λ6585)在LAMOST的观测波长范围内. 为了标记LAMOST星系光谱的年龄和金属丰度, 我们将LAMOST 星系光谱与SDSS DR16发布的光谱数据进行交叉. 为了减小同一天体的LAMOST观测光谱和SDSS观测光谱的信噪比差别, 按照两者信噪比之差小于等于3的条件筛选交叉得到同源光谱.最终得到约2万条LAMOST光谱及其同源SDSS光谱. 对于这些LAMOST光谱进行退红移, 然后对光谱进行重采样, 波长范围3800–7000 ˚A, 采样间隔为1.5 ˚A. 这些处理后的LAMOST光谱作为实验样本建立深度学习回归预测模型.
2.2 年龄和金属丰度的标记
本文的目标是对筛选得到的约2万条LAMOST光谱建立回归预测模型,估计星系的年龄和金属丰度, 那么首先需要标记这些样本的两个物理参数的真实值. 我们使用经典的全谱匹配方法PPXF[4]对这些LAMOST光谱的同源SDSS光谱计算其年龄和金属丰度, 作为LAMOST星系物理参数的真实值. PPXF的原理是利用模型谱拟合观测谱, 这个模型谱是由多个不同年龄、不同金属丰度的简单星族(Simple Stellar Population,SSP)组合而成.在本文工作中, SSP取自Vazdekis等人在2010年[17]提出的基于经验恒星光谱库MILES (Medium resolution INT Library of Empirical Spectra)的模型谱, 我们选用36条SSP, 其中包含了9个年龄(Age= 0.06、0.12、0.25、0.5、1.0、2.0、4.0、8.0、15 Gyr), 4个金属丰度(Z=-1.71、-0.71、0、0.22 dex, 标准化到太阳金属丰度尺度: lg (Z/Z⊙),其中Z⊙表示太阳金属丰度,Z⊙= 0.019 dex). 使用这些模型谱对SDSS星系光谱进行拟合, 最终得到了最佳拟合所对应的加权平均的年龄和金属丰度,将这些年龄和金属丰度作为LAMOST光谱年龄和金属丰度的真实值.
2.3 卷积神经网络设计
深度学习是一种具有很强特征学习能力的技术, 尤其是在计算机视觉和语音识别等应用领域中都表现得非常突出. 它采用了权值共享的方式, 减少了权值的数量使得网络容易优化, 自动从数据中学习特征, 并可以将结果向同类型数据进行泛化.深度学习被广泛地应用于天文领域, 提供了大数据时代解决问题的新思路[18–19]. 本文将卷积神经网络应用于星系星族参数的回归预测研究.
回归预测模型属于有监督学习, 通过训练大量的有标签星系光谱, 从而获得识别无标签光谱物理参数(年龄和金属丰度)的能力, 因此它可以比较准确地给出星系光谱的物理参数. 该模型由8个卷积层、4个池化层、1个全连接层组成, 其网络结构图如图2所示.
在图2中卷积层(Convolution)和池化层(Max-Pool)上方显示了形如a@b*c的数字, 其中a表示卷积核的个数,b*c表示数据为b×c维, 全连接层(Dense)和输出层(Output)上方显示了形如b*c, 表示数据为b×c维.网络的输入是LAMOST星系光谱,每条光谱是2134×1向量,输出是光谱的年龄和金属丰度预测值. 卷积层中的卷积核的数量增加后又减少, 前2个卷积层中有16个长度为3的卷积核, 经过池化层后输入到2个卷积层(具有64个长度为3的卷积核), 再经过池化层输入到2个卷积层(具有128个长度为3的卷积核), 最后再经过一层池化层输入到2个卷积层(具有64个长度为3的卷积核). 经过前面若干次卷积和池化后, 数据进入全连接层和输出层, 最终得到年龄和金属丰度的预测值.

图2 卷积神经网络结构图Fig.2 Architecture of CNN
卷积层的激活函数是线性整流函数(Rectified Linear Unit,ReLU),其表达式为f(x)=max(x,0),其中max是取最大值的函数,x为上一层网络的输出. ReLU给神经元引入了非线性因素, 这样可以逼近任何非线性函数, 使神经网络更好地应用于非线性的光谱参数测量中. 该模型采用Adam优化器, Adam是一种自适应并且稳定的算法, 综合了动量梯度下降学习的稳定及其学习率随着训练次数和维度的变化而变化的特点. 损失函数采用均方误差损失函数(Mean Squared Error, MSE), 损失函数MSE用来衡量的是真实值与预测值的差异. 训练模型时评价函数采用决定系数R2(coefficient of determination),度量训练过程的回归效果,当R2接近1表示预测值和真实值非常接近.
3 实验与结果分析
实验在一台处理器Intel®CoreTMi7-10700F CPU@2.90 GHz×16, 内存32 GB的电脑上进行.
实验样本包括约2万条LAMOST光谱, 按照2:8划分测试集和训练集,Strain={(x(i),yi),i=1,··· ,N}表示训练集, (x(i),yi)是一个训练样本, 其中x(i)= (,··· ,)是n维向量, 表示第i条光谱的流量,yi表示与x(i)对应的物理参数(年龄和金属丰度)的真实值,N表示训练集中所包含的光谱数量.Stest={(x(i),yi),i=1,··· ,M}表示测试集,M表示测试集中所包含的光谱数量.
3.1 模型的评价标准
我们使用测试集评价深度学习模型的预测效果, 本文采用均方根误差(RMSE)、平均绝对误差(MAE)和标准差(SD)这3种评价指标, 定义如下:

3.2 结果分析
3.2.1 卷积神经网络回归预测结果分析
采用上述设计的卷积神经网络结构对实验样本进行训练, 训练后的模型对测试数据集的预测结果如图3所示. 图3左边子图是真实年龄和预测年龄的对比图, 右边子图是真实金属丰度和预测金属丰度的对比图. 两图中黑色虚线均表示真实值和预测值相等. 真实值和预测值的3种评价指标RMSE、MAE和SD位于图的左上角. 从图3中可以看出, 预测结果比较好, 基本上没有系统偏差, 均方根误差、平均绝对误差和标准差都在0.16 dex以内. 由此可见, 使用我们设计的卷积神经网络回归模型对LAMOST光谱测量星族年龄和金属丰度与传统的星族合成方法得到的值基本一致. 这表明对于流量定标不准确的星系光谱数据, 有监督的深度学习方法可以比较准确地测量出其物理参数.
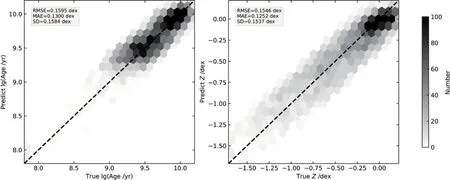
图3 卷积神经网络模型预测结果. 左边子图是年龄的预测值与真实值的对比, 右边子图是金属丰度的预测值与真实值的对比. 注意, 图中去掉了3σ以外的点.Fig.3 Results of CNN. The left panel is the comparison of age between predicted values and true ones, and the right panel is the comparison of metallicity between predicted values and true ones. Note that points out of 3σ are clipped in each panel.
本文方法的预测精度(0.16 dex)优于文献[16]提出的基于小尺度特征的模板匹配方法(0.2 dex),并且信噪比低至5时本文方法对年龄和金属丰度的误差在0.18 dex (此结果来自下一节实验), 而文献[16]在信噪比低至5时的年龄误差为0.25 dex, 金属丰度误差为0.3 dex, 由此可见本文方法在低信噪比时明显优于文献[16]. 另外, 我们在相同实验设备配置下测量两种方法的用时, 结果表明本文方法的时间复杂度明显低于文献[16]: 本文方法对上述2万条LAMOST光谱训练模型并且预测参数共耗时约3 h, 而使用文献[16]方法得到1条光谱的星族参数就需要约1 min. 本文方法的用时大部分在模型训练上, 一旦模型训练好了, 后续的参数估计用时非常少. 由此可见, 本文方法在计算上具有很大优势.
3.2.2 卷积神经网络回归模型的适用性分析
我们对上述卷积神经网络回归模型的适用性分别从信噪比和星系类型两个方面展开. 首先, 分析模型对不同信噪比光谱的预测效果. 按照r波段信噪比区间[5, 10)、[10, 15)、[15, 20)、[20, 25)、[25,30)、[30,-)将测试集分为6部分,对该模型进行测试. 预测值与真实值的差别随着信噪比的变化如图4中实线所示. 可以看出, 随着信噪比的增大, 误差呈下降趋势, 年龄和金属丰度误差在信噪比为5时最大, 在0.18 dex以下. 这一测试结果表明该模型在不同信噪比下均有比较好的预测效果.
图4中虚线表示测试集样本的年龄和金属丰度的内禀弥散随信噪比的变化. 如前所述, 年龄和金属丰度的标签值是由PPXF拟合LAMOST同源的SDSS光谱得到的, 为了求两个参数的内禀弥散, 我们对每一条SDSS光谱按照其误差分布重新采样100次, 然后用PPXF重复测量, 取标准差作为年龄和金属丰度的内禀弥散值. 从图4可以看出, 随着信噪比的增大, 年龄和金属丰度的内禀弥散呈下降趋势, 除了信噪比为5时两个参数的内禀弥散略大(低于0.07 dex), 其他情况下内禀弥散均低于0.05 dex. 而且随着信噪比的增大, CNN的预测误差(实线)越来越接近内禀弥散(虚线), 说明对于高信噪比光谱, CNN的预测值越来越接近给定的标签值.

图4 卷积神经网络模型预测误差随着信噪比的变化. σ(ΔAge)表示年龄(lg (Age))的预测值和真实值差别的标准差, σ(ΔZ)表示金属丰度(Z)的预测值和真实值差别的标准差.Fig.4 Dispersion of the differences of the stellar population parameters predicted by CNN as a function of S/Nr. σ(ΔAge)represents the standard deviation of the differences between predicted age (lg (Age)) and true ones, and σ(ΔZ) represents the standard deviation of the differences between predicted metallicity (Z) and true ones.
接下来我们分析该模型对于不同类型星系的预测效果. 首先按照文献[14]提出的分类策略, 根据Hα是否是发射线将星系数据分成吸收线星系(absorption-line galaxies)和发射线星系(emission-line galaxies), 然后基于BPT图采用Kauff-mann等[20]和Kewley等[21]提出的经验分割线, 将发射线星系分为star-forming (SF)、composite和AGN 3类. 表1给出了模型对这4类星系光谱进行预测得到的年龄和金属丰度值和真实值的差别. 可以看出, 模型对于不同类型星系的参数预测值与真实值基本一致, 误差在0.18 dex左右, 其中对吸收线星系的预测误差最小, 对AGN预测误差略大. AGN预测误差相对较大可能是因为AGN训练样本数量较少(占总样本数的3%), 因而构建CNN模型时AGN的特征学习不全面导致的.

表1 卷积神经网络回归模型对不同类型星系的参数预测结果Table 1 Prediction results based on CNN for different types of galaxies
3.2.3 卷积神经网络与其他机器学习算法的比较
为了验证卷积神经网络在星族参数学习中的优势, 我们使用另外两种机器学习算法: 随机森林回归模型和深度神经网络, 对比3种算法对星族参数的预测效果.
DNN也可以称为多层感知机(Multi-Layer Perceptron, MLP), 是一种全连接的神经元结构,第j(j= 1,··· ,K -1,K表示网络总层数)层的任意一个神经元一定与第j+1层的任意一个神经元相连. 这里使用的DNN的网络结构有输入层、输出层和3个隐藏层, 其中每个隐藏层的神经元均为1024个, 输入层和输出层与卷积神经网络设计一致: 输入LAMOST光谱即2134×1向量, 输出为年龄和金属丰度.
随机森林回归模型(RFR)属于Bagging类算法, 集成了多个决策树. 在训练阶段, 算法使用bootstrap采样从输入数据中选择多个不同的子数据集对多个不同决策树进行依次训练; 在预测阶段, 算法将内部多个决策树的预测结果取平均值作为最终随机森林回归模型的预测结果. 本文随机森林回归算法中设置ntree=100,即决策树个数为100.
将随机森林回归模型和深度神经网络用于本实验样本中, 数据集划分与卷积神经网络一致, 3种算法的评价指标值如表2所示. 可以看到年龄和金属丰度两个参数的3个评价指标中卷积神经网络算法最小, 说明卷积神经网络预测结果的离散程度比其他两个算法小, 它在星系星族参数的评估精度上有着较大的优势.
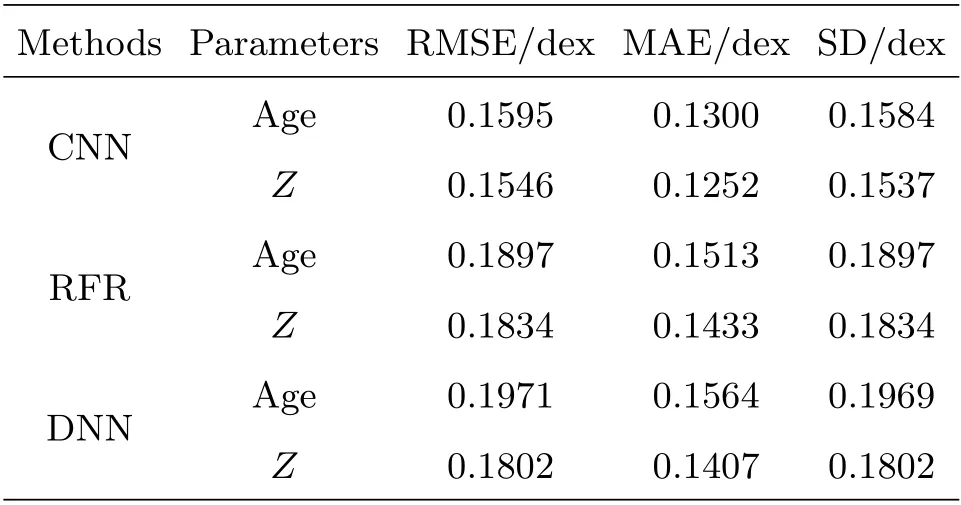
表2 卷积神经网络、随机森林回归模型和深度神经网络的结果对比Table 2 Comparison of experiment results based on CNN, RFR and DNN
4 总结与展望
本文使用了卷积神经网络对2万条LAMOST星系光谱进行回归分析, 实验显示卷积神经网络对年龄预测的RMSE、MAE和SD分别为0.1595、0.1300、0.1584, 对金属丰度预测的RMSE、MAE和SD分别为0.1546、0.1252、0.1537, 并且随着光谱信噪比的增大, 预测误差越来越小. 另外, 将本文建立的卷积神经网络回归模型与随机森林回归模型和深度神经网络的预测结果进行比较, 从总体来看优于其他两种模型, 说明卷积神经网络模型对星系的星族物理参数(年龄和金属丰度)的预测效果更好. 我们将此深度学习模型用于LAMOST新的巡天星系光谱上, 实现星系年龄和金属丰度的自动测量. 在下一步的工作中, 我们将继续完善深度学习模型. 例如在深度学习的模型构建时我们使用PPXF 全谱匹配方法计算SDSS光谱的年龄和金属丰度作为LAMOST同源光谱的真实值, 而这种方法得到的真实值是存在一定误差的, 可以尝试使用星族模板直接合成模拟光谱及其内禀参数值作为训练数据来构建星系参数回归模型. 另外, 使用深度学习方法除了估计星系的年龄和金属丰度外, 我们还计划对星系其他参数如速度弥散、恒星形成率等进行回归预测.

