雄安新区vS30经验估计研究

张 肖,张 合,刘思宇,刘书峰

(1.昆明理工大学 公共安全与应急管理学院,云南 昆明 650500;2.雄安新区震灾预防中心,河北 雄安新区 071700;3.河北省震灾风险防治中心,河北 石家庄 050021)

0 引言

规划建设雄安新区是千年大计、国家大事。河北雄安新区位于京津冀地区核心腹地,该地区覆盖层厚,对地震波有明显的放大作用,且周边曾发生过1679年三河—平谷8级地震、1966年邢台6.8级地震和1976年唐山7.8级地震。雄安新区地下管廊较多,可达地下三层。建筑物由于其所在工程场地土层浅部特征的不同,在地震中受到的破坏程度也不同。场地条件是影响地震动特征和结构震害的重要因素,因此研究场地条件对地震动的影响和震害评估意义重大。由于土层的等效剪切波速(vS)与场地放大效应具有良好相关性[1],因此土层等效剪切波速成为研究场地条件、进行场地分类的首选参数,是工程项目建设抗震设计的重要参数。

我国现行的建筑抗震设计规范[2]中,场地分类采用20 m深度的等效剪切波速vS20和覆盖层厚度共同确定,将场地类型分为四类。而美国、欧洲、新西兰等国家和地区的抗震设计规范则以vS30为参数进行工程场地类别判断和地震动衰减关系计算,其中美国建筑抗震设计规范(简称NEHRP)[3],依据vS30将场地分为五类。这种差异使我国相关专业的科研人员在选择、对比和应用国外研究成果时会遇到场地分类和参数不统一等诸多问题;另外,研究表明,上覆30 m土层对地震动峰值影响显著,大于30 m的土层影响明显减弱[4-5]。随着我国经济的发展,建筑结构类型发生了变化,超高层建筑、大跨度桥梁日益增多,这些结构占地大、自振周期长,而所涉及的场地条件很可能有较大差别;且随着中国扩大开放,有些工程需要同国际相关标准对接,因此仅仅计算vS20已不再满足很多工程建设需求,开展vS30研究显得尤为迫切,也符合我国现在国情。

然而,由于相关技术限制、场地环境问题、超出设置的速度阈值和预算约束等条件的制约[6],很多地区的钻孔深度不足30 m,因此如何合理准确地应用不足30 m的近地表剪切波速剖面估算等效剪切波速vS30成为十分重要和迫切的问题。随着工程地震的发展,国内外学者基于众多剪切波速剖面达到30 m深度的场地数据,采用回归分析拟合出vS30和vSz(z<30 m)的经验关系,以用于当钻孔深度未达到30 m时估算vS30值[6-9]。而这些估算模型是否适用于雄安新区有待进一步验证。

本文选取雄安新区起步区区域性地震安全性评价工程中435个钻孔,分别计算出20 m和30 m深度内的等效剪切波速,分析vS20和vS30的相关性。结合常速度外推模型(以下简称BCV模型)、速度梯度外推模型(以下简称Boore 2004和Boore 2011)、双深度参数模型(以下简称Wang 2015)进行vSE30计算,研究各估算模型的可靠性和适用性。

1 区域数据资料

雄安新区位于河北省中部,地势平坦,区域内皆为平原区,自西北向东南略有倾斜,海拔高度5～26 m。区内主要河流有大清河、小白河及漕河等,区内大部分平原为这些河流洪积、冲积或泛滥作用形成,为冲洪积平原。平原区中第四纪总厚度一般为600 m以上,覆盖层厚度很大。

本文收集2020—2021年雄安新区起步区区域性地震安全性评价项目中435个钻孔资料,这些钻孔终孔深度均大于30 m,波速资料和土层信息完整,钻孔终孔深度最小80 m,最大100 m。图1为钻孔位置分布图,图2为钻孔深度统计分布图。从图2可以看出,终孔深度主要集中在85～92 m间。雄安新区钻孔均达到30 m以上,因此可以按式(1)、(2)直接计算vS30[2]。

图1 钻孔位置分布图(引用河北省地震局工程院图件)Fig.1 Spatial distribution of boreholes

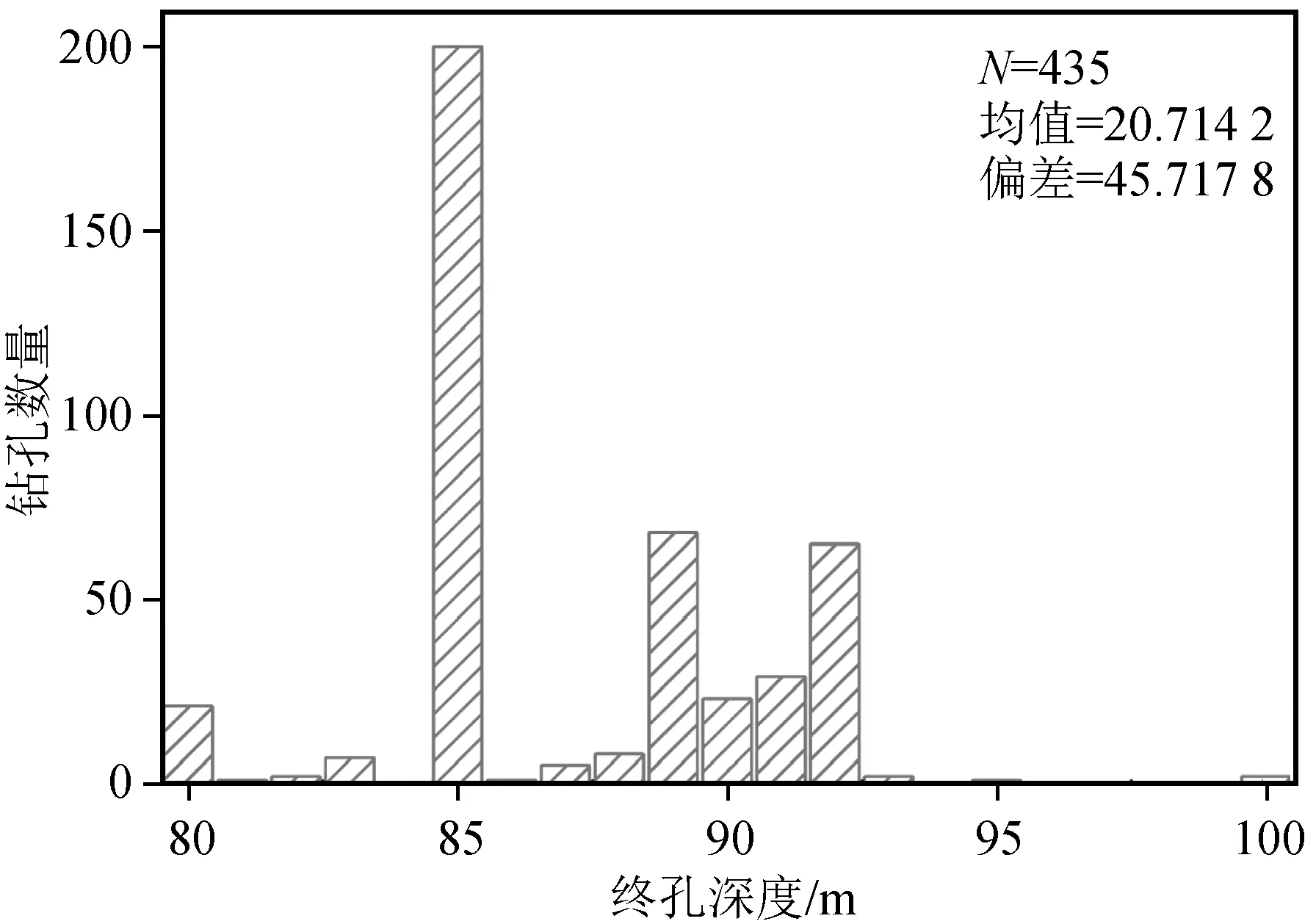
图2 不同深度终孔数量分布图Fig.2 Number of boreholes at different depths

(1)

(2)

式中:t(30)为剪切波速在地表至30 m深度的传播时间(s);dz为某一土层的厚度(m);vSz为该土层的剪切波速(m/s)。

由于我国场地类别是按vS20的等效剪切波速和覆盖层厚度进行划分的,因此在进行场地划分时根据美国国家地震减灾计划(NEHRP)基于vS30定义的场地分类进行划分(表1)。

表1 美国抗震规范场地类别划分标准Table 1 The site classification standard of American seismic code

根据公式(1)、(2)计算20 m和30 m深度的等效剪切波速,分析vS20和vS30的相关性(图3),并结合表1和vS30实测值进行场地类别划分。vS20和vS30的关系式为:y=1.118 07x-0.898 71,相关系数r=0.865 7,较接近于1,说明二者相关性较好,且vS30比vS20大10%左右。基于 NEHRP进行场地分类,雄安新区起步区均为D类场地。

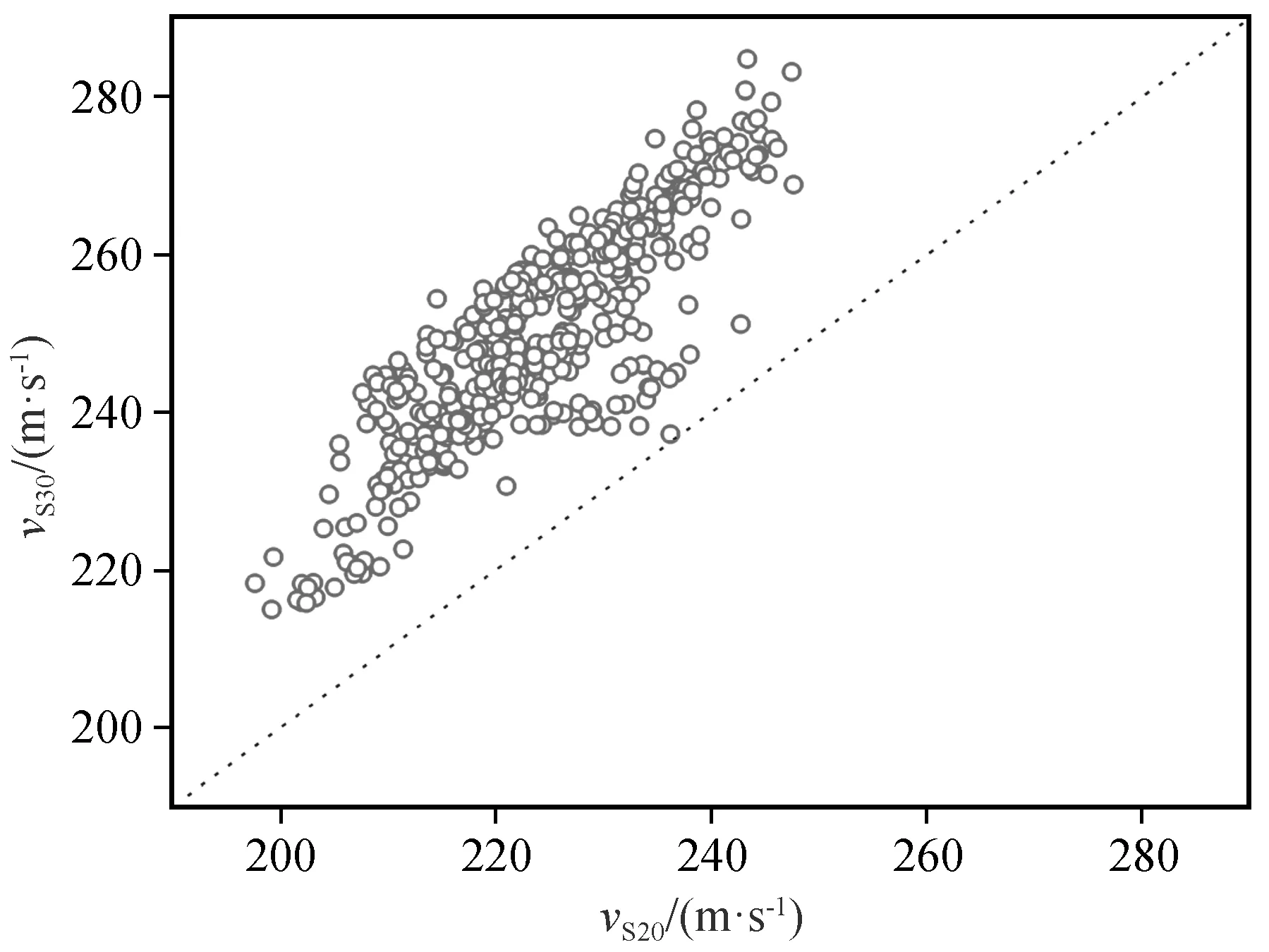
图3 vS20和vS30的对应关系图(虚线代表1∶1分割线)Fig.3 Relation of vS20 to vS30(Dashed lines represent the 1∶1 curve)

2 vS30经验估算方法

当钻孔测井深度大于30 m时可以直接计算vS30。但很多地区可能会存在钻孔深度未达到30 m,此时如何获得vS30国内外众多学者对此进行了研究,并尝试给出多种不同的估算模型。比较有代表性的有常速度模型、速度梯度外推模型、双深度参数模型。本文采用这3种模型计算vSE30,并与vS30进行相关性分析,判断vS30估算模型的适用性。

(1) 常速度外推模型

地表到深度z的平均剪切波速vSz的计算公式为:

(3)

其中:到深度z处的走时t(z)为:

(4)

式中:z通常是指速度模型底部的深度;vSz是指某土层的剪切波速度。

如果钻孔探测井深度仅达到了z(小于30 m),则30 m等效剪切波速估算值vSE30可以通过以下公式进行推算[10]:

(5)

式中:veff为深度z到30 m的等效速度。为了计算方便,将钻孔最底层的波速值代替等效速度。

(2) 速度梯度外推模型

Boore 2004利用式(6)对某一深度处平均剪切波速vSz和vSE30之间的对数线性统计关系模型建立了加州地区剪切波速经验关系[7]:

lgvSE30=a+blgvSz

(6)

式中:vSz为不同深度处的平均剪切波速;a和b均为回归系数[7]。

Boore 2011对日本KiK-net钻孔数据研究发现,对于一个给定深度的vSz,得出的vS30总是系统地高于加州、土耳其、欧洲等地区,说明场地速度梯度变化是存在区域差异的。Boore 2011中给出两组方程,其中第一组适用于当对场地类别一无所知时使用,而另一类需考虑E类场地(NEHRP场地分类中,当vS30<180 m/s时为E类场地)。式(7)中的二次回归方程计算日本地区的剪切波速经验关系[6]:

lgvSE30=c0+c1lgvSz+c2(lgvSz)2

(7)

式中:c0、c1及c2均为日本地区回归系数[6]。

Boore 2011认为通过目视可以确定某场地划分为E类(这些地点通常被泥浆和淤泥所覆盖,如在河口和河流三角洲附近)。鉴于E类场地的独特性,Boore 2011推导出所有站点(包括E类)的vSz回归方程,但对于E类场地使用了虚拟变量,拟合方程如式(8)[6]:

lgvSE30=c0EδE+c0+c1lgvSz+c2(lgvSz)2

(8)

式中:对于E类场地,δE=1,否则,当为其他场地时,δE=0。KIK-Net 场地的系数和残差标准差参见文献[6]。

(3) 双深度参数模型

Wang 2015则用两个不同深度z1和z2的(本文称之为深度组合)等效剪切波速为参数,提出了一个估算vSE30的新方法。首先假定到深度z处的平均剪切波速计算公式为[9]:

lgvSz=lga+blgz

(9)

式中:a和b都是回归系数。

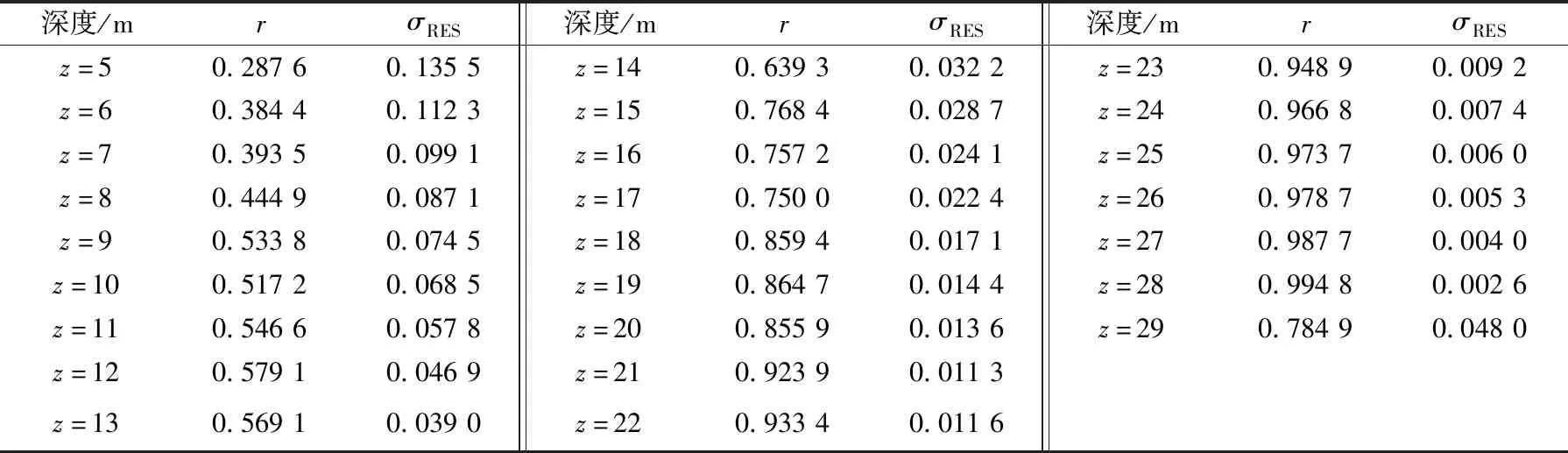
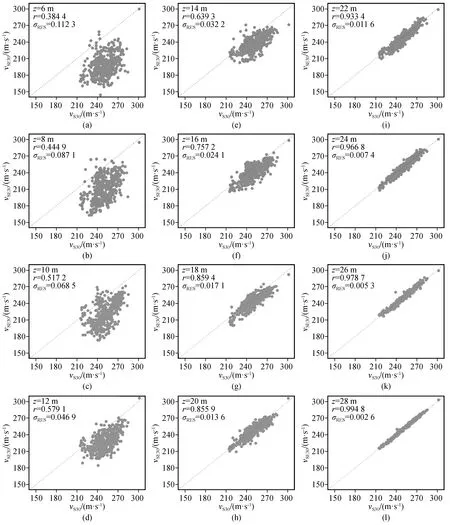
已知在两个不同深度的平均剪切波速vS(z1)和vS(z2),且z1

(10)

(11)

将式(10)、(11)代入,则vSz的计算公式为:

lgvSz=lgvS(z2)+

(12)

令z=30 m,则vSE30可由式(12)计算出。

由于式(12)是一个简单的外推函数,用于计算深度z处的vSz不需要任何回归分析来确定式(9)中的系数a和b。

(4) 可靠性分析

要判断哪种经验估计公式更适合雄安新区区域场地,需要将3种估算模型得出的vSE30和测量值vS30进行可靠性和相关性分析。皮尔森相关系数r及二者的残差标准差σRES可由式(13)、(14)计算得出[9]:

(13)

(14)

式中:xi、yi分别为估算值vSE30和测量值vS30;N为雄安新区起步区区域性地震安全性评价中钻孔总数。

3 vSE30估算模型可靠性分析

利用雄安新区435个钻孔资料,通过上述3种估算模型,结合不同深度计算vSE30,并与实测计算值vS30做相关性分析,获得皮尔森相关系数和残差标准差,最后比较这3种估算模型的适用性。

通过BCV模型计算雄安新区起步区435个钻孔在不同深度(5～29 m)时,外推得到的30 m深度处的等效剪切波速vSE30,并将其与vS30进行比较,绘出6、8、10、12、14、16、18、20、22及24 m散点图(图4),并计算vSE30和vS30的皮尔森相关系数和残差标准差(表2)。

表2 BCV模型法vS30与vSE30的相关系数及残差标准差Table 2 Correlation coefficient and residual standard deviation of vS30 and vSE30 from BCV model

图4 不同深度下BCV模型得到的vSE30和vS30对比图Fig.4 Comparison between vSE30 and vS30 from BCV model at different depths

通过BCV模型计算出vSE30和vS30的相关性有如下特征:

(1) 当z<29 m时,随着深度的增加,vSE30和vS30的皮尔逊相关系数会增大,残差标准差会减小;当深度20 m

(2) 当钻孔剖面深度较小时,vSE30和vS30的离散性较大,且偏离1∶1分割线较远,随着深度的增加,vSE30和vS30的离散性越来越小,当达到28 m时基本分布于1∶1分割线上。

应用速度梯度外推模型、双深度参数模型计算雄安新区vSE30,获得各模型的皮尔逊相关系数和残差标准差(表3、表4);采用速度梯度外推模型、双深度参数模型计算得到的vSE30与vS30的相关性(图5)。

图5 不同深度下不同模型vSE30和vS30对比图Fig.5 Comparison between vS30 and vSE30 from different models at different depths

表3 速度梯度外推模型vSE30与vS30相关系数及残差标准差Table 3 Correlation coefficient and residual standard deviation of vS30 and vSE30from models of Boore 2004 and Boore 2011

表4 双深度参数模型vSE30与vS30相关系数及残差标准差Table 4 Correlation coefficient and residual standard deviation of vS30 and vSE30 from model of Wang 2015

用各估算模型计算出的vSE30与vS30之间的相关性有如下特征:

(1) 对于速度梯度外推模型给出的各类vS30经验估算模型,皮尔逊相关系数都会随着钻孔剖面深度的增加而增加,残差标准差会随之减小。当z≤23 m时,应用Boore 2011方程计算的皮尔逊相关系数大于Boore 2004,当z≥24 m时,应用Boore 2004和Boore 2011公式计算的皮尔逊相关系数均相等。

(2) 速度梯度外推模型中,考虑不同参数情况下皮尔逊相关系数均相等,说明无论选择Boore 2011中哪个参数进行讨论均不会对皮尔逊相关系数造成影响,而对于残差标准差的值,则需考虑E类场地<不考虑场地分类<非E类场地。

(3) 双深度参数模型中,随着深度组合(z1、z2)中某一个或两个值的增加,皮尔逊相关系数会随之增大,而残差标准差则会减小。当深度组合(z1、z2)中某一个值或两个值接近30 m时,皮尔逊相关系数越大,则残差标准差越小。深度组合(20、25 m)的皮尔逊相关系数达到0.979 3。

(4) 当式(12)中z2等于式(6)～(8)中的z时,即:将双深度参数模型中深度组合(5、10 m)、(10、15 m)、(15、20 m)、(20、25 m)分别与速度梯度外推模型中10、15、20、25 m作相应比较。除了深度组合(5、10 m)与10 m对比时,皮尔逊相关系数和残差标准差略差外,双深度参数模型的皮尔逊相关系数均比速度梯度外推模型方法得到的值要大,残差标准差也均小于速度梯度外推模型。

4 各估算模型的优势和局限性

任何经验模型都有优势和局限性,通过vSE30和vS30之间的相对误差(Rerror)来进行研究[9]。方法如下:

(15)

相对误差Rerror越小,说vSE30和vS30越接近,该方法也越有优势。

由于BCV模型在雄安新区适用性相对较差,因此在进行模型评价时暂不予考虑。根据雄安新区起步区435个钻孔数据,结合速度梯度外推模型不同深度(10、15、20、25 m)与双深度参数模型(5、10 m;10、15 m;15、20 m;20、25 m)4个深度组合的vSE30相对误差见表5、图6。通过对比可以发现:

图6 各估算模型相对误差柱状图Fig.6 Histogram of the relative error of vSE30 estimated by each model

表5 各模型估算出的vSE30的相对误差范围Table 5 The relative error range of vSE30 estimated by each model

(1) 无论对于哪种模型,随着深度的增加,vSE30的相对误差会逐渐减小,当深度达到25 m时,相对误差均达到10%以内。

(2) 速度梯度外推模型中,Boore 2004 方程估算出的4个深度的vSE30相对误差在0.02%～19.86%。

而Boore 2011中,不考虑场地分类的相对误差在0.09%～29.05%,考虑E类场地的相对误差在0.01%～21.61%,考虑非E类场地的相对误差在0.09%～48.95%;双深度参数模型估算出的4个深度组合的vSE30相对误差在0%～26.56%。Boore 2011考虑E类场地相对误差明显小于其他两个参数相对误差。速度梯度外推模型略小于双深度参数模型的vSE30相对误差。

5 讨论和结论

5.1 讨论

(1) BCV模型中，当钻孔剖面的深度z满足：z≤20 m 时皮尔逊相关系数较小；20 m

(2) 速度梯度外推模型中，当z≤23 m时应用Boore 2011模型计算的皮尔逊相关系数大于Boore 2004；当z≥24 m时Boore两个模型计算的皮尔逊相关系数均相等，但Boore 2004 计算所得残差标准差要小于Boore 2011，Boore 2011模型中，考虑不同参数情况下皮尔逊相关系数均相等。说明无论选择中哪个参数进行讨论，对皮尔逊相关系数无影响，而残差标准差的值则为：考虑E类场地<不考虑场地分类<非E类场地。

Boore 2004 方程估算出的4个深度的vS30相对误差在0.02%～19.86%范围内，而Boore 2011中，不考虑场地分类的相对误差在0.09%～29.05%范围内，考虑E类场地的相对误差在0.01%～21.61%范围内，考虑非E类场地的相对误差在0.09%～48.95%范围内。

因此，结合皮尔逊相关系数、残差标准差和相对误差综合考虑，在雄安新区场地Boore 2004 略优于Boore 2011。

双深度参数模型中，随着深度组合(z1、z2)中某一个值或两个值接近30 m时，皮尔逊相关系数越大，残差标准差越小。深度组合(20、25)的皮尔逊相关系数达到0.979 3；当将双深度参数模型中深度组合(5、10)、(10、15)、(15、20)、(20、25)分别与速度梯度外推模型中10、15、20、25作相应比较。除了深度组合(5、10)与10 m对比时皮尔逊相关系数和残差标准差略差外，双深度参数模型的皮尔逊相关系数均比速度梯度外推模型方法得到的值要大，残差标准差也均小于速度梯度外推模型。

双深度参数模型估算出的4个深度组合的vS30相对误差在0%～26.56%范围内。因此，无论是皮尔逊相关系数、残差标准差还是相对误差分析，均发现双深度参数模型明显优于其他模型，所以该模型更适用于雄安新区场地。

5.2 结论

本文给出的结果表明，双深度参数模型比BCV模型、速度梯度外推模型的效果更适用于雄安新区。这是由于地质和岩土工程的原因，剪切波速随着深度的增加而增加，而BCV方法直接用钻孔最底层z处的波速按常数外推至30 m，低估了vS30。

速度梯度外推模型是基于大量场地的钻孔剖面资料通过回归分析来确定模型相关系数，由于场地间的差异性，该模型不可避免地存在偏差。Boore 2004是基于加利福尼亚、土耳其和欧洲的场地数据获得的经验模型，而Boore 2011适用于日本KiK-net台网，所以推断雄安新区场地可能与加利福尼亚、土耳其等场地有相似处。

双深度参数模型是采用不同深度两个已知剪切波速，基于直线斜率的对数域里的线性外推函数,该模型不需要大量场地数据进行拟合回归，因此更适合雄安新区。