地震作用下双层土裂缝边坡稳定性分析

梁承龙,刘 芳

(广西交通职业技术学院 土木建筑工程学院,广西 南宁 530012)

0 引言

长期以来土坡稳定性是岩土工程中的一个热门问题,许多学者对此做了大量研究[1-3]。极限分析以其便捷的运算被广泛应用于土坡稳定性研究。极限分析通过构建运动许可的速度场直接求解极限状态下的极限荷载,所求的极限荷载是不小于真实值的上限解。最早由Drucker等[4]提出极限分析理论,随后Chen[5]运用极限分析理论详细研究了岩土体边坡的稳定性,并证明出二维土坡最危险滑动面是一条对数螺旋线。

裂缝边坡普遍存在于实际工程之中,研究表明裂缝的存在会降低边坡稳定性。Utili[6]综合研究了裂缝深度和位置对边坡稳定性的影响。Michalowski[7]论述了孔隙水压力及裂缝形成对边坡稳定性的影响。Zhao等[8]分析了地震作用下边坡稳定性并得出地震效应将大幅度降低边坡稳定性。罗强等[9]探讨了坡顶超载对均质土坡稳定性的影响。基于非线性Mohr-Coulomb屈服准则,Li等[10]分析了孔隙水作用下裂缝边坡稳定性;李得健等[11]研究了地震效应下裂缝边坡稳定性。然而,实际中土体表现出某种程度的各向异性以及非均质性,上述研究都是针对均质土坡,因此得出的结果较为保守同时也会造成一定的经济损失。Chen[5]给出了非均质和各向异性土坡的稳定系数。栾茂田等[12]进行了阻滑桩加固非均质各向异性土坡稳定性分析并得出最优加固位置。夏元友等[13]提出了水平条分极限分析方法研究非均质性及各向异性锚固边坡抗震稳定性。王珍等[14]采用拟合多项式近似描述对数螺旋线对非均质边坡稳定性上限分析评价研究。

以上研究均针对土体黏聚力的非均质性和各向异性,而实际工程中往往存在不同土层,且由于工程的需要会形成诸多的人工边坡,边坡土体内摩擦角不再为固定值。基于传统极限分析所推导出的对数螺旋线滑动面要求破坏土体保持恒定内摩擦角,即不考虑内摩擦角的非均质性,导致无法针对此类边坡进行稳定性分析。孙志彬等[15-16]提出离散运动学机构,以“点到点”逐步生成滑动面用以解决边坡稳定性分析中内摩擦角非均质性问题。Qin等[17-19]基于离散运动学机构采用拟动力法考虑地震力作用下边坡稳定性。侯超群等[20]针对分层多级复杂边坡进行稳定性分析。

上述研究中鲜有对分层土裂缝边坡的稳定性进行研究,因此本文基于极限分析上限定理和离散运动学机构,以双层土边坡为例,研究地震力作用下裂缝边坡稳定性问题,通过二分法和优化算法相结合求解边坡临界高度和安全系数,并与传统上限法对比验证本文计算方法的有效性,探讨了双层土的分布变化对裂缝边坡的稳定性以及裂缝深度和位置的影响规律。

1 离散运动学机构

与传统上限法不同,本文中边坡破坏时滑动面不再预先假设为对数螺旋线滑动面,而是根据“点到点”生成一系列离散点逐步构成滑动面,同时离散点生成过程也符合边坡破坏过程:边坡发生破坏时,先由坡趾附近发生剪切破坏,滑动面再由下向上、由外向内逐渐延伸至坡顶[21]。图1所示为边坡离散运动学机构模型。以边坡发生坡底破坏为例建立直角坐标系,坐标原点为D(0,0)。边坡坡趾为C并建立坡角为β、坡高为H的边坡模型。由此可知,当D与C重合时边坡破坏由坡底转向坡趾,即β′=β。

如图1所示,给出“点到点”生成滑动面具体过程。

图1 裂缝边坡离散机构Fig.1 Discrete kinematic mechanism of cracked slope

根据所建立的直角坐标系,由变量θ0和r0确定破坏土体的旋转中心O坐标(xO,yO):

(1)

式中:r0为O到D的距离;θ0为OD与水平方向的夹角。以固定角度增量Δθ=0.1°由左向右逐个生成所有离散点,同时也保证了滑动面生成的准确性[15]。破坏土体视为刚体且土体满足Mohr-Coulomb屈服准则。已知滑动面上一点Pi,对应角度为θi,由相关联流动法则可以得到Pi处的速度vi与滑动面Pi+1Pi方向的夹角为内摩擦角φi,与滑动面Pi+1Pi单位外法线Ni方向成π/2+φi:

(2)

(3)

(4)

式中:ω为角速度。根据向量关系并结合式(1)～(4),可由Pi坐标(xi,yi)得到Pi+1坐标(xi+1,yi+1):

(5)

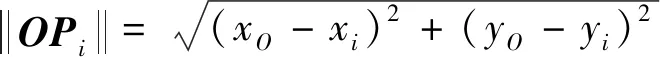
(6)

由于本文考虑坡顶处存在垂直张拉裂缝,因此引入变量d来描述裂缝的深度。因此,裂缝深度为H-d。当Pi的纵坐标yi大于等于d时,采用线性插值法调整点Pi坐标使之纵坐标满足yi=d,与之对应的横坐标:

xi=ΔD+xc

(7)

式中:ΔD为D到C的距离;xc为裂缝到C的横向距离。由于是垂直裂缝,在裂缝面上生成的离散点横坐标保持不变,纵坐标增量Δy可由几何关系得到:

Δy=(xi-xO)·[tan(θi+Δθ)-tanθi]

(8)

当Pi的纵坐标yi大于等于边坡高度H时停止离散点的生成。若yi>H,则采用线性插值法调整点Pi坐标使之纵坐标满足y=H。

2 离散上限法求解内外功率

极限分析上限定理可描述为对任一满足运动许可的破坏机构,令外功率等于内能耗散率,便可求得不小于真实值的极限荷载上限解。因此,根据构建的离散运动学机构,需分别求出外功率包括破坏土体ABCDE重力做功功率和地震力做功功率以及由土体沿破坏面所产生内能耗散率。其中,采用拟静力法考虑地震力作用。如图2(a)所示为内外功率计算简图,图2(b)为双层土体参数,其中γ1、c1和φ1分别为上层土的土体重度、黏聚力和内摩擦角;γ2、c2和φ2分别为下层土的土体重度、黏聚力和内摩擦角。根据Qin等[17]所述,将坡底破坏区域分成三个区域:区域Ⅰ、区域Ⅱ和区域Ⅲ。以区域Ⅲ为例求解四边形块体PiPi+1Qi+1Qi外功率和内能耗散率。

图2 计算简图Fig.2 Calculation diagram

在坡面上分别生成与Pi(xi,yi)和Pi+1(xi+1,yi+1)相同纵坐标的Qi(x′i,y′i)和Qi+1(x′i+1,y′i+1),由几何关系得:

(9)

(10)

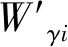
Wγi=ωγiAi(xGi-xO)

(11)

(12)

式中:γi为重心Gi处的土体重度;Ai由海伦公式求得;kv和kh分别为地震竖直加速度系数和地震水平加速度系数。

同样的方法求得三角形PiQiQi+1重力做功功率W″γi和地震力做功功率W″ei,因此,四边形块体PiPi+1Qi+1Qi的外功率Wi可表示为:

Wi=W′γi+W″γi+W′ei+W″ei

(13)

其内能耗散率Di可表示为:

(14)

式中:ci为Pi+1Pi中点对应的土体黏聚力。对于区域Ⅰ和区域Ⅱ,N(xN,yN)为滑动面最低点,NN′代替边坡坡面,此时由Pi(xi,yi)和Pi+1(xi+1,yi+1)所得到Qi(x′i,y′i)和Qi+1(x′i+1,y′i+1)分别为:

(15)

(16)

将求得的Qi和Qi+1替换至区域Ⅲ便可求得相应的外功率和内能耗散率。因此,令外功率等于内能耗散率可得到边坡临界高度Hcr:

∑Wi=∑Di

(17)

式中:∑Wi为外功率之和;∑Di为内能耗散率之和。实际工程中,边坡安全系数更受工程师的青睐。结合强度折减法,将土体实际抗剪强度c和φ折减到土体处于极限平衡状态下的抗剪强度cd和φd,折减系数为安全系数FS:

(18)

式中:c和φ分别为实际土体的黏聚力和内摩擦角;cd和φd分别为处于极限平衡状态下土体的黏聚力和内摩擦角。结合式(17)和式(18),相应变量分别为r0、θ0和d,通过二分法和优化算法迭代求解出边坡临界高度Hcr和安全系数FS[15,20]。

3 对比验证与分析

3.1 验证

为了验证上述离散运动学机构和计算方法的正确性,将本文中的土坡退化成均质土坡计算所得结果与传统上限法结果进行对比。表1和表2分别给出了由传统上限法和离散上限法所求得的边坡临界高度Hcr安全系数FS的对比。由表1和表2可知,两种方法计算结果非常接近,且本文结果略小于传统上限法所得结果,即本文结果的优越性且更加接近于真实值,从而充分验证了本文构建的离散的优越性机构和计算方法的有效性。

表1 边坡临界高度Hcr对比Table 1 Comparison between the critical height Hcr of different slopes

表2 边坡安全系数FS对比Table 2 Comparison between the safety factor FS of slopes

3.2 地震力的影响

以文献[23]中的算例为模型对双层土裂缝边坡的稳定性进行研究,具体模型参数如图3所示。由图4可知,本文所得安全系数小于文献[23]的结果,且临界滑动面处于更深处。由于上下土层的内摩擦角不同,在土层分界处滑动面出现明显的变化。在地震力作用下,边坡安全系数降低,破坏面向边坡内部移动,表明边坡破坏范围增大,从而破坏程度更加严重。同时,可以从图4和图5中看出,上层土的滑动面变化较为明显,原因在于上层土的黏聚力与内摩擦角较小,从而土体的抗剪强度较低,在受到地震力的作用下更容易破坏;图5所示,当考虑坡顶存在裂缝时,随着地震力的增大裂缝深度略微加深,裂缝位置逐渐远离坡面。

图3 模型参数Fig.3 Model parameters

图4 无裂缝边坡临界滑动面Fig.4 Critical sliding surface of slope without cracks

图5 裂缝边坡临界滑动面Fig.5 Critical sliding surface of cracked slope

3.3 深度系数的影响

将上下土层分界处高度与边坡高度比值定义为深度系数Δ,探究其对边坡安全系数及裂缝深度和位置的影响。如图6和图7所示,随着深度系数Δ的增大,边坡安全系数FS增大,但增大的幅度逐渐减小。对于无裂缝边坡而言,当Δ≥0.8时,边坡安全系数FS基本保持不变。而对于裂缝边坡,边坡安全系数在Δ>0.8有所减小。同时,随着地震力作用的增大,安全系数FS随之略微降低。由此可知,在上软下硬双层土中,边坡安全系数对深度系数的变化较为敏感。当深度系数较小时,由上层软土主导,边坡整体抗剪强度较低,导致安全系数较低;随着深度系数的增大,下层硬土占比增加,从而整体提高边坡的稳定性,因此安全系数增加。图8给出不同参数组合下裂缝边坡安全系数随深度系数增大的变化。由图8可得,无论是双层土坡的特性是上软下硬或是上硬下软,都存在一个特定的深度系数Δ*,使得边坡安全系数达到最值。例如,在本文算例中,对于上软下硬双层土坡,当Δ*=0.8时安全系数达到最大值。而对于上硬下软双层土坡,当Δ=Δ*时安全系数取到最小值。同时结合图6和图8可以得到,Δ*的取值与坡顶是否存在裂缝和坡角无关。

图6 深度系数对不同坡角边坡安全系数的影响Fig.6 Effect of depth coefficient on the safety factor of slope with different slope angles

图7 深度系数对裂缝边坡安全系数的影响Fig.7 Effect of depth coefficient on the safety factor of cracked slope

图8 不同参数组合下深度系数对裂缝边坡安全 系数的影响Fig.8 Effect of depth coefficient on the safety factor of cracked slope under different combinations of parameters

图9和图10给出了双层土的抗剪强度变化对安全系数的影响。从图9和图10中可以看出,随着上层土抗剪强度增大,同一深度系数Δ下边坡安全系数FS增大。且随着Δ的增大,FS逐渐趋向于均质土坡的安全系数。原因在于Δ的增大改变了上下土层厚度的占比,对于上软下硬双层土,下层厚度增加,边坡整体抗剪强度增大,FS随之增大;相反,对于上硬下软双层土,边坡整体抗体强度减小,进而FS减小。

图9 不同黏聚力比下深度系数对裂缝边坡安全系数的影响Fig.9 Effect of depth coefficient on the safety factor of cracked slope under different cohesion ratios

图10 不同上层内摩擦角下深度系数对裂缝边坡安全系数的影响(φ2=20°)Fig.10 Effect of depth coefficient on the safety factor of cracked slope under different internal friction angles of upper layer (φ2=20°)

图11给出了深度系数Δ对裂缝深度和位置的影响。由图11可知,随着深度系数Δ的增大,裂缝深度整体呈现减小趋势,裂缝位置逐渐靠近坡面;在Δ≥0.8时,裂缝深度出现突增,裂缝位置也随之突变靠近坡面,此时裂缝穿越至下土层;原因在于当Δ<0.8时,裂缝深度未触及到上下土层分界处,上下土层共同提供抗剪强度,此时边坡稳定性随着下层硬土比例增加而提高,裂缝深度降低;当Δ≥0.8时,下层硬土增加比例显著减缓,边坡逐渐趋向于均质边坡,裂缝向下延伸至下方土层,上层土不再提供抗剪强度。除此之外,随着坡脚β的增大,裂缝的范围逐渐靠近坡面。

图11 深度系数对裂缝深度和位置的影响Fig.11 The effect of depth coefficient on depth and location of the crack

4 结论

本文基于极限分析上限定理,构建了地震作用下双层土裂缝边坡离散破坏机构,采用“点到点”生成临界滑动面,分析了地震作用下土体非均质性对裂缝边坡稳定性的影响;结合拟静力法和强度折减法求解得到边坡临界高度和安全系数上限解,探讨了土体非均质性和双层土深度系数对边坡稳定性及裂缝深度和位置的影响,得到以下主要结论:

(1) 裂缝的存在会降低边坡的稳定性,且随着地震力的增大,边坡安全系数显著降低,临界滑动面加深,从而加剧了边坡失稳。对于上软下硬双层土边坡,临界滑动面的变化有所不同:经过下层土的滑动面基本保持不变,而经过上层土的滑动面随地震力的增大变化明显,逐渐远离坡面。

(2) 随着地震力的增大,裂缝深度略微增大,裂缝位置逐渐远离坡面。对于具体的双层土边坡,无论是否考虑坡顶存在裂缝,均存在一个特定的深度系数Δ*使得边坡安全系数达到最值,且其与坡顶是否存在裂缝和坡角无关。在本文算例中,对于上软下硬双层土坡,Δ*=0.8,边坡安全系数达到最大值。当Δ<Δ*,裂缝处于上层土中且裂缝深度随着Δ的增大而减小;当Δ≥Δ*,裂缝将穿越至下层土,裂缝深度由最小值发生突增。