兰州重塑黄土抗拉强度冻融特性与衰减模型研究——基于轴向压裂法

吴旭阳,任明洋,黄俊杰,梁庆国,王 园

(1.河南城建学院土木与交通运输学院,河南 平顶山 467036;2.兰州交通大学土木工程学院,甘肃 兰州 730070;3.河南城建学院材料与化工学院,河南 平顶山 467036)

0 引言

随着我国西部大开发战略的实施,在黄土地区建设高速公路,不可避免地要进行大量开挖,在季节性冻土分布区,太阳辐射和地表状况有明显的日变化和季节性变化,土体的冻结与融化反复进行,将会对土体的物理力学性质产生重要影响[1-2]。已有研究表明,冻融循环作用对黄土黏聚力[3-4]及无侧限抗压强度[5]具有弱化作用,对内摩擦角影响不大[6-7]。随着冻融循环次数的增加,黄土冻结过程中冰晶冻胀力破坏土体结构[8-10],融化时结构不可恢复,反复冻融是造成土体强度弱化主要原因。从微观角度来看[11-12],随着冻融次数的增加,土体孔隙中的大孔径先减少,后增多;小孔径先增多,后减少,最后向5～10 μm范围内集中。另外,冻融循环会造成土样原孔隙扩展、伸长、分叉、贯通[13],黄土的原始胶结结构逐渐被破坏[14],颗粒重新排列,土的结构越来越疏松,颗粒之间原始固有胶结逐渐减弱,造成黏聚力不断降低。综合黄土冻融特性的研究成果来看,黄土的抗剪强度、无侧限抗压强度、压缩性[15]、孔隙特征分布、微观结构特性、湿陷性[16]等方面备受研究人员关注,并取得了可喜研究成果,对季节冻土区黄土路基冻融病害防治具有重要指导意义。然而对于黄土路堑边坡剥落病害,最主要是由坡面黄土在冻融条件下强度劣化引起[17],且大部分学者[17-20]都从抗剪强度冻融弱化的角度出发去阐释边坡剥落的机理,而边坡剥落通常发生在表层,在这个过程中,黄土边坡的剥落灾害是在表层黄土颗粒拉-剪耦合作用下发生,黄土的抗拉强度在冻融过程中的弱化也起到了关键作用,但是目前关于黄土抗拉强度冻融特性的研究鲜有报道。另外,对原状黄土路堑边坡来说,坡面不同程度的剥落病害极大地影响了黄土边坡的整体稳定性[18],极有可能导致边坡整体发生滑移而影响公路的正常使用,对过往的行人和车辆也是一种潜在的危险[19],同时剥落也降低了坡面的美观程度,不符合现代公路建设“安全、环保、舒适、和谐”的要求。所以,对黄土抗拉强度冻融衰减特性的研究可以为边坡剥落病害提供更合理的解释,研究成果也能够为工程防治措施提供更好的指导建议。

1 试验材料及试验方法

1.1 土样来源及物理特性

试验用黄土取自兰州市和平镇路堑边坡,该边坡高约80 m。有研究表明,季节性冻黄土区域内最大冻深一般在1 m以内,故此次试验用土取自坡顶平缓位置,地下2 m深度处未经冻融过的黄土。该地区为Q3黄土,土质呈褐黄色,塑限15.36%,液限28.67%,塑性指数13.30,最优含水量16.5%,最大干密度1.75g·cm-3,颗粒密度2.72 g·cm-3。颗粒级配采激光测分仪测定结果如图1所示。

图1 颗粒级配曲线Fig.1 Particle-size distribution curve

1.2 试验方法及试样制备

1.2.1 试验方法

抗拉强度采用轴向压裂法间接测定[图2(b)],试样直径控制为6.18 cm,高度6.25 cm,加载柱为直径1.545 cm,高度2 cm的刚性圆柱,轴心对中环采用内直径为1.55 cm,厚度0.2 cm的铝制空心圆环,抗拉强度试验在GTS万能试验机上进行[图2(a)],通过刚性加载柱施加轴向荷载,加载速率控制为1.0 mm/min,抗拉强度计算公式为[21-22]:

图2 GTS万能试验机试验过程Fig.2 Test process using the GTS universal testing machine

(1)

式中:σt为抗拉强度(kPa);P为荷载(N);K为与土壤类别性质相关的参数,本试验取1[23];b为试样半径(cm);H为试样高度(cm);a为加载圆柱半径(cm)。

1.2.2 试样制备

试样制备采用静压制样法。首先,控制含水量分别为:11%、13%、15%、17%、19%,相同含水量下控制干密度分别为:1.55 g·cm-3、1.60 g·cm-3、1.65 g·cm-3、1.70 g·cm-3、1.75 g·cm-3;冻融循环次数分别设计为0次、1次、3次、5次、7次、11次、15次,每个试样设计一个平行样,取其测定值的平均值作为最终抗拉强度值,试验依次共完成350个样品。将制好的试样用保鲜膜紧贴试样包裹,而后用宽胶带绕缠密封[图2(c)],防止在冻融过程中水分散失,最后设定冻结12小时融化12小时为一次冻融循环,冻结过程将试样置于-16 ℃冷冻恒温冰箱中[图2(d)],融化过程置于室温(25 ℃)自由融化(由于试验期间为6月至9月之间,室外温度相对较高,满足融化过程需要),待冻融循环次数达到目标要求,即进行抗拉强度试验。

2 试验结果与分析

2.1 抗拉强度与冻融循环的关系

2.1.1 冻融循环对抗拉强度-贯入深度特性的影响

文中贯入深度指上下加载柱沿试样轴线的相对位移。以含水量15%，干密度1.60 g·cm-3的试样为例,由图3可看出,抗拉应力随贯入深度的增大而增大,达到峰值强度后有一陡降过程,陡降幅度达到其抗拉强度的1/3,而后随贯入深度的增加呈上凸型逐渐减小,这是因为加载柱下方楔形体形成后相对移动过程中与劈裂面土颗粒相互摩擦作用引起,该过程残余抗拉强度主要由摩擦强度组成,就其强度值而言,未冻融的黄土抗拉强度最高可达16.9 kPa,冻融一次降低幅度最大,降为13.1 kPa,而后冻融3次以后抗拉强度降到最低且基本趋于稳定,稳定于12 kPa左右。对于其抗拉强度随贯入深度发展关系而言,图4可看出,抗拉强度随贯入深度的增加先由A点线性增大至B点,而后BC段相对平缓,而后由C点近似线性增至峰值抗拉应力D点(抗拉强度),在此过程中,AB段可认为弹性阶段,即刚性柱与试样接触并压缩的初始阶段,BC段为加载柱上下方土体逐渐压缩挤密[21],即楔形体形成阶段,在此之前试样轴向加载抗力主要由形成楔形体过程中的剪切力承担,C点之后,楔形体形态基本形成,并沿轴线相对运动,从而产生劈裂力,CD段主要试样主要在楔形体作用下处于受拉状态,D点达到抗拉强度,从试样随贯入深度变化的形态来看,试样在达到抗拉强度之前,外边没有明显裂纹出现,当达到抗拉强度D点时,试样表面初始裂纹出现,而后裂纹迅速扩张,同时伴随拉应力急剧减小至E点,此时试样上下裂纹贯通,在此之后(EF段)拉应力随贯入深度呈现上凸型减小,这是由于此时试样内部抗力主要有楔形体楔形剪切面与颗粒摩擦产生,此过程中的试样残余抗拉强度已经非常小。F点以后抗拉应力随贯入深度的增大呈下凹式减小,并伴随试样拉裂纹宽度逐渐增大,最终至试样完全破裂为两瓣或者三瓣,轴向压裂法测定黄土抗拉强度试验结束。

注:DR为冻融次数图3 不同冻融循环次数下拉应力与贯入深度Fig.3 Relationship between tensile stress and penetration depth under different freeze-thaw cycles

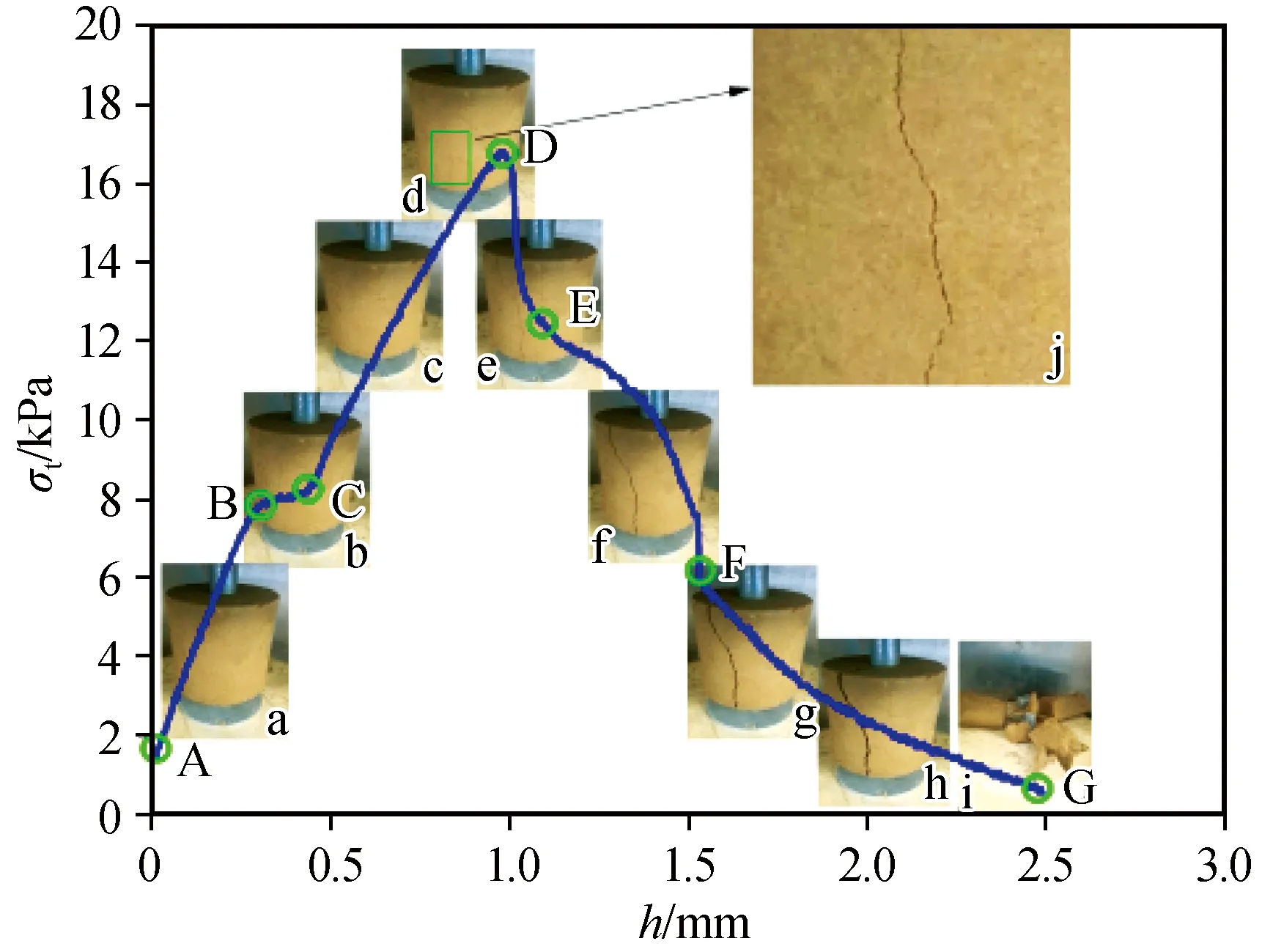
图4 试样随贯入深度的破坏过程Fig.4 Failure process of specimen with penetration depth

2.1.2 冻融循环对抗拉强度的影响

取不同含水量及不同干密度下350个试样抗拉强度随冻融循环变化的试验数据,取平行试验平均值作为该试样真实抗拉强度值,共175个数据点,根据同一干密度进行分组,每组每个含水量下不同冻融循环次数为一单组如图5所示。干密度1.55 g·cm-3时抗拉强度随冻融循环次数的增加衰减程度较小,基本没有变化,随着干密度的增大,冻融作用逐渐显著。

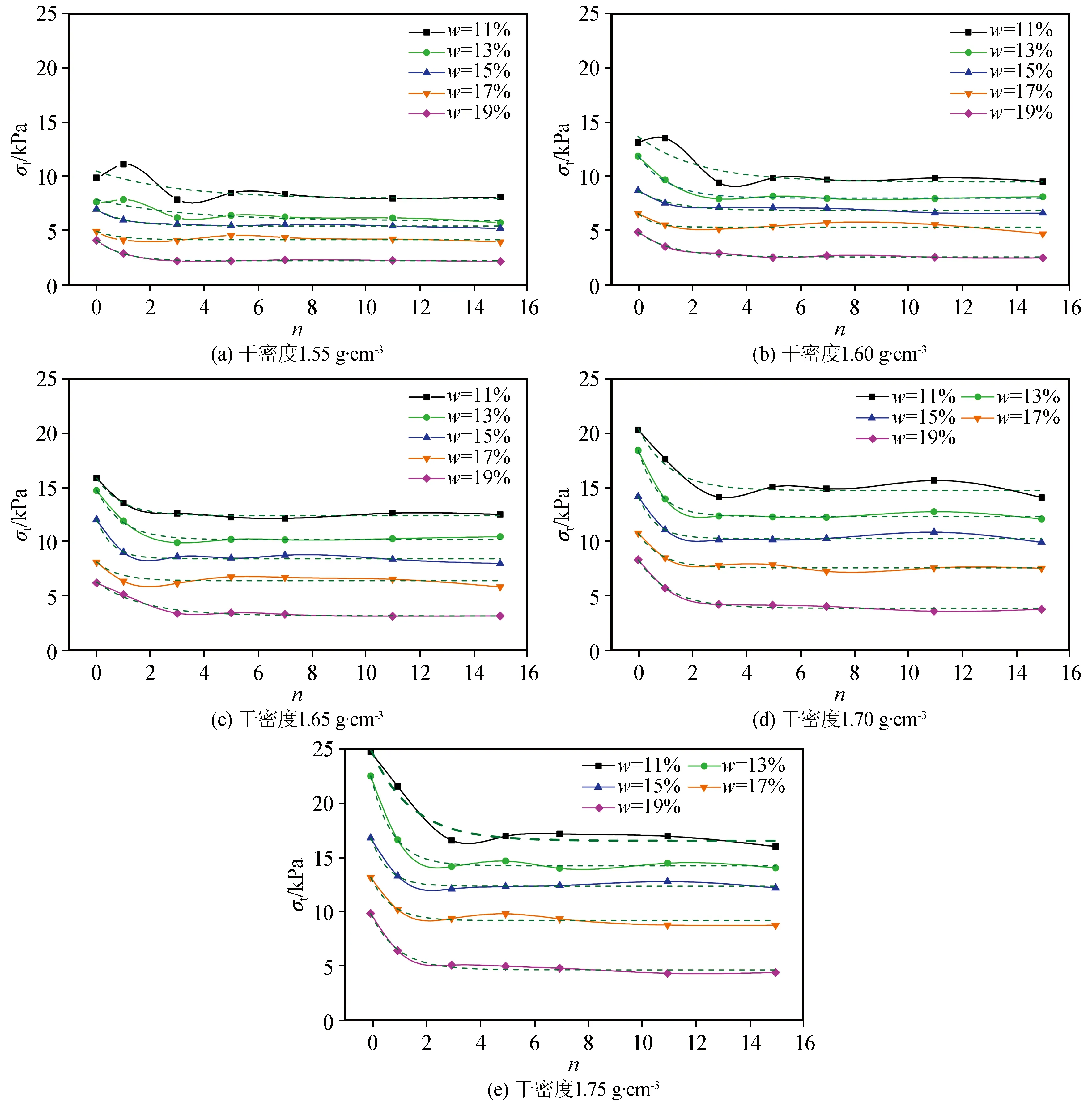
图5 不同干密度下冻融循环次数(n)对抗拉强度的影响Fig.5 Effect of freeze-thaw cycles (n) on the tensile strength under different dry densities

干密度为1.55 g·cm-3含水量11%和13%及干密度1.60 g·cm-3含水量11%条件下试样在冻融一次时抗拉强度最高,在经历三次冻融循环时抗拉强度减小至最低值,由此说明冻融作用对黄土颗粒间抗拉接触黏结具有弱化作用,冻融循环四次以后其抗拉强度基本稳定。对于含水量相对较大(w=15%、w=17%、w=19%)的黄土抗拉强度在经历1次冻融循环后强度呈衰减状态,且在基本均是在3次冻融作用时强度降至最低,而后随冻融作用的增加变化幅度不大,这是由于含水量较大时颗粒之间的孔隙相对较小,土颗粒外侧水膜厚度较大,颗粒间分子引力及颗粒间的接触黏结强度均较大,也就是说颗粒骨架较强,故其未冻融时的抗拉强度较大,在冻结过程中,初始含水量可能达到或者大于土样起始冻胀含水量,土样会在冻结过程中发生冻胀,由于外部温度低,内部温度高,从而引起水分由试样中心向外缘冻结面迁移,在此过程中土样自身原有颗粒间黏结结构遭到破坏,大颗粒团簇结构会破碎,颗粒之间裂隙增多,间距增大,颗粒与颗粒之间的排列方式发生改变,在融化过程中,冰融化成水,体积减小形成孔隙,在水分迁移力作用下部分土颗粒会在融化过程中填充这些孔隙,然后有大量孔隙无法填充,这是造成黄土冻融衰减的主要原因,故在冻融1次、3次作用下其抗拉强度均呈减小状态,含水量15%的土样在超过3次冻融循环后其抗拉强度随冻融次数的增多或略微增大或持续减小,然而就其强度大小而言,基本趋于稳定。不同含水量及干密度下黄土抗拉强度随冻融循环次数均呈指数衰减关系,指数衰减方程为:σt=ae(-n/b)+c,具体系数如表1所列。

表1 各干密度与含水量下抗拉强度随冻融循环的指数衰减系数Table 1 The exponential attenuation coefficient of tensile stren-gth with freezing-thawing cycles under different drydensities and different water contents

2.2 冻融循环对抗拉强度衰减率的影响

冻融循环下强度衰减率通过下式计算:

(2)

式中:Ψ为冻融衰减率(%);σ0为未冻融时的强度值(kPa);σn为冻融n次时的强度值(kPa)。

由抗拉强度不同含水量不同干密度在经历各次冻融循环后的衰减程度可看出(图6),抗拉强度衰减率在3次冻融时达到最大,而后在5次冻融后有所提高,最终稳定。其中干密度1.55 g·cm-3的抗拉强度衰减率在经历多次冻融后相对最小,最终稳定于20%左右；而干密度1.60 g·cm-3、1.65 g·cm-3、1.70 g·cm-3、1.75 g·cm-3冻融衰减率则在一次冻融时衰减程度最大,可达15%～20%,3次冻融时衰减率最大,可达30%以上。含水量19%时,冻融作用对其强度衰减程度影响较大,随着冻融次数的增加强度衰减率持续增大,最终可达50%左右。图6(e)可看出含水量较高时冻融作用对其强度影响不大,这是由于含水量超过临界值后其强度本身就很低,而经历冻融作用后从其强度值方面看确实变化不大,但是如果从其衰减程度上看,其衰减率时最高的,由此可见,含水量越大,冻融作用越明显。

现将不同含水量不同干密度下抗拉强度在多次冻融循环后的最大衰减率列于表2中,可看出,不同含水量下抗拉强度最大衰减率的方差与变异系数均相对较小,由此可将黄土按照含水量不同而区分其最大冻融衰减率,即用同一含水量下不同干密度在多次冻融循环后的最大衰减率的平均值作为该含水量下的一般最大冻融衰减率。由表1可知,含水量11%,13%、15%、17%时抗拉强度最大衰减率在30%左右,而当含水量19%时,抗拉强度最大衰减率较大在52%左右。

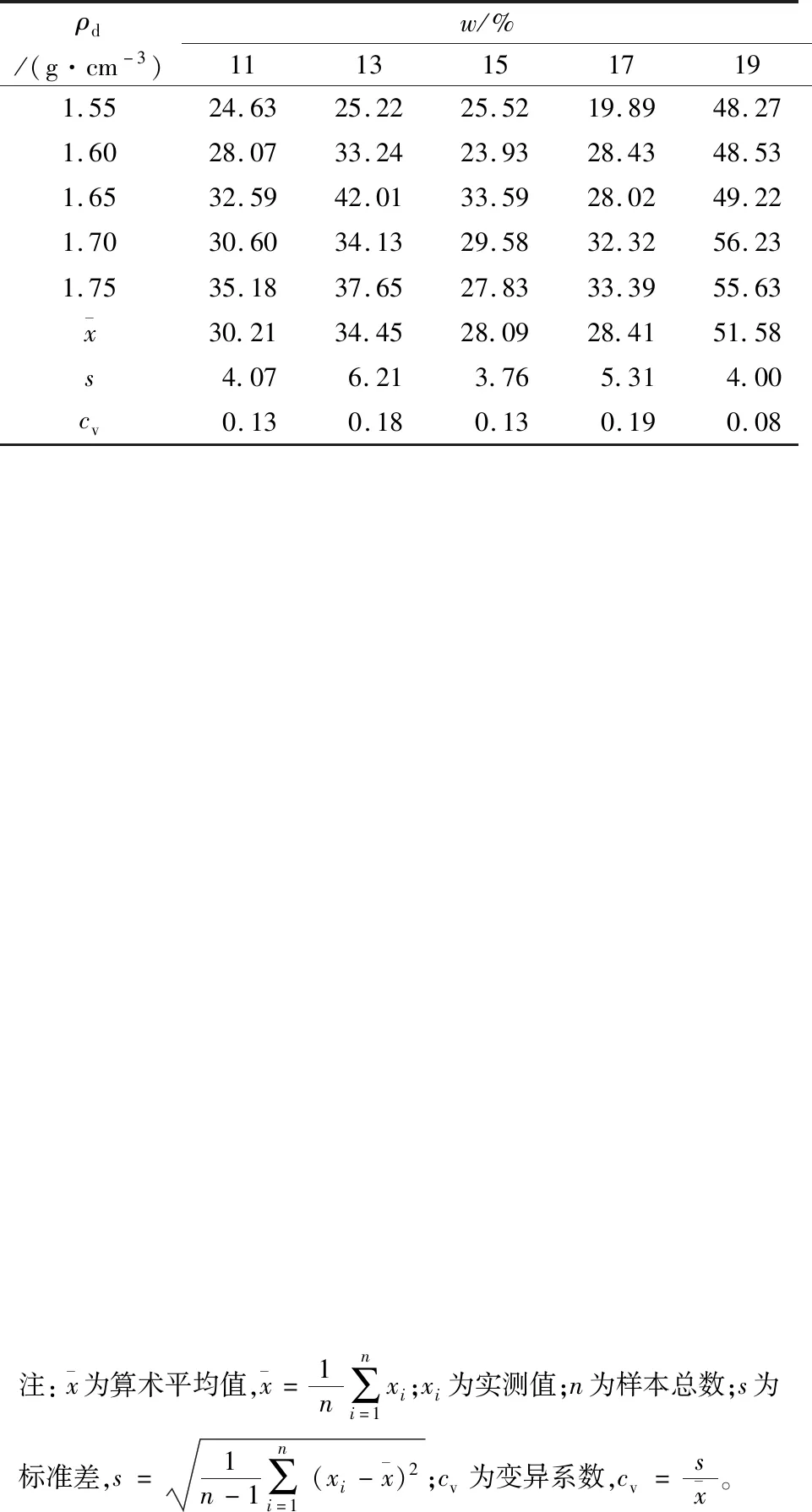
表2 不同含水量及干密度的最大冻融衰减率Table 2 Maximum freezing-thawing attenuation rate under different water contents and different dry densities

2.3 黄土抗拉强度冻融衰减模型

2.3.1 单因素抗拉强度冻融衰减模型

为探究不同含水量与相同冻融循环条件下其抗拉强度衰减率的关系,现对已有数据进行如下处理:首先将同一含水量相同冻融次数不同干密度的强度衰减率取平均值,用来近似反映在某一含水量及冻融循环次数下的强度衰减率,而后通过该平均值结合不同含水量及冻融循环次数进行整理,结果如图7所示,含水量19%时,每次冻融造成的抗拉强度衰减率均最大。1次冻融时,含水量11%的抗拉强度衰减率最小,接近5%,含水量13%、15%、17%的抗拉强度衰减率比较接近,接近18%。冻融3次后不同含水量衰减程度差异表现出来,其中含水量13%、15%、17%时抗拉强度衰减率随含水量的增大而减小,含水量11%的抗拉强度衰减率处于第三位,19%含水量时抗拉冻融衰减率最大。15次冻融循环时,11%、13%、15%、17%含水量下冻融衰减率基本处于30%左右,19%含水量下冻融衰减率处于52%。由以上分析可知,含水量19%时与其他含水量的强度冻融衰减率在不同冻融循环次数下有较大差异,故将19%含水量的强度衰减率单独指数衰减拟合。将11%、13%、15%、17%含水量下随冻融循环次数的强度衰减率进行全部数据指数衰减拟合,得出的拟合结果如图7所示,并将拟合参数列于表3中。通过拟合方程来近似反映黄土不同含水量下强度衰减率随冻融循环次数的增加而变化的量化规律。由表3中拟合参数可看出,参数a与c的绝对值相差不大,差值平均为0.6%,故将a与c的绝对值简化为等值,即冻融循环对黄土强度衰减率的影响可通过下式描述:

表3 不同含水量下冻融衰减率的拟合参数Table 3 Fitting parameters of freezing-thawing attenuation ratio under different water content

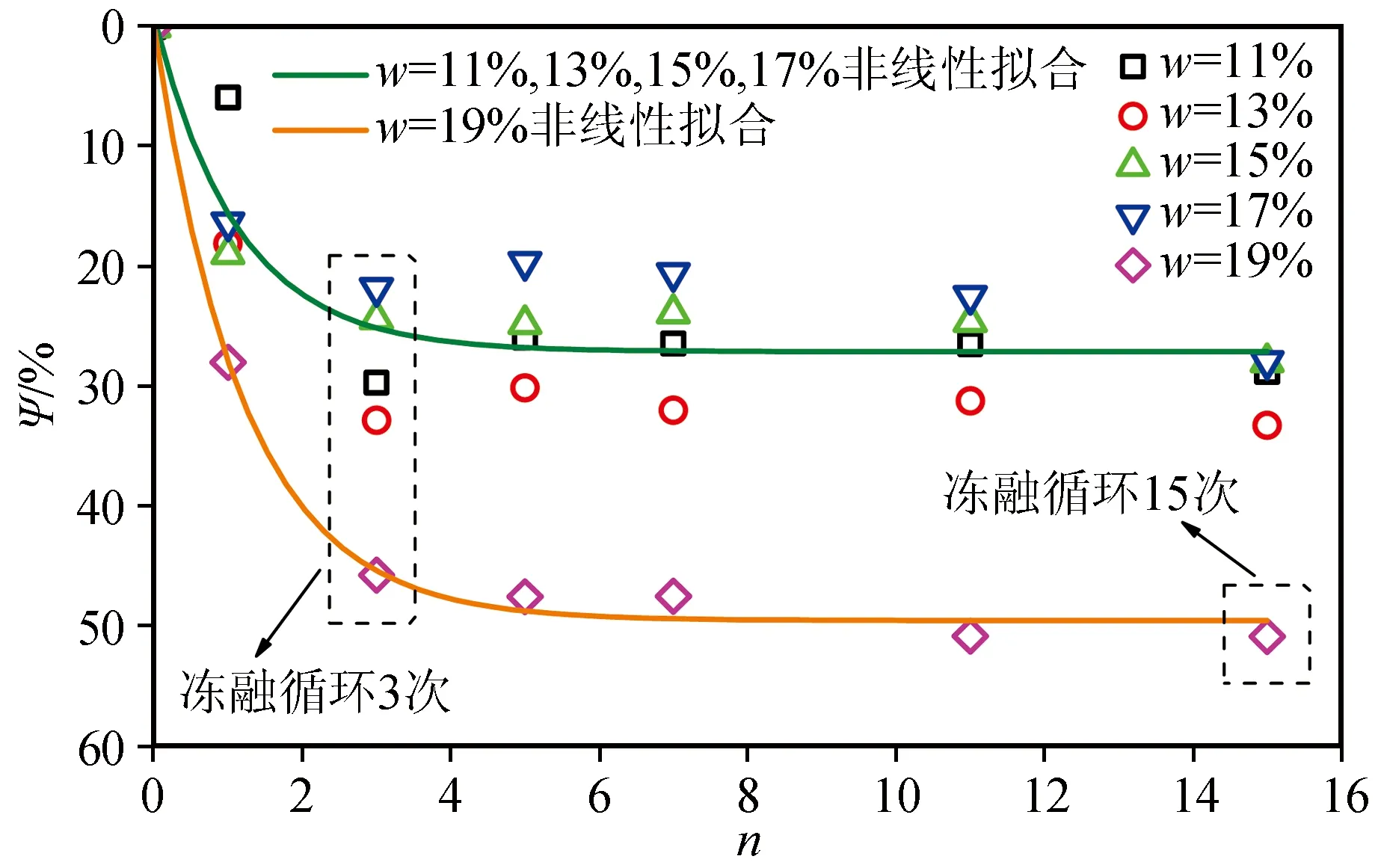
图7 不同含水量下抗拉强度衰减率与冻融循环 次数的关系Fig.7 Relationship between the attenuation rate of tensile strength and the number of freezing-thawing cycles under different water contents

Ψ=a[e(-n/b)-1]

(3)

2.3.2 多元抗拉强度冻融衰减模型

以上研究均以控制变量为核心,即控制含水量不变探讨干密度变化是对抗拉强度的影响或者控制干密度不变探讨含水量对抗拉强度的影响。然而实际上干密度与含水量对黄土强度的影响同时存在,为探究黄土抗拉强度与含水量和干密度的多元相关关系,通过Tablecurve3D 可得出未冻融情况下抗拉强度、含水量、干密度多元三维空间分布情况,如图8(a)所示,可看出黄土强度随含水量的减小及干密度的增大呈螺旋状上升趋势,通过对所生成曲面进行三维多元非线性拟合可看出[图8(b)],抗拉强度随含水量及干密度服从多元非线性方程:

图8 未冻融时含水量、干密度与抗拉强度的多元非线性关系Fig.8 Multivariate nonlinear relationship among the water content,dry density,and tensile strength without freezing and thawing

(4)

相关系数均达到0.99以上。

如果引入冻融循环衰减率变量(Ψ),则可近似求解各种含水量及干密度条件下在不同冻融情况下的抗拉强度值,即:

σt-n=σt-0(1-Ψσt)

(5)

式中:σt-n为冻融n次时的黄土抗拉强度值;σt-0为未冻融时的黄土抗拉强度值;Ψσt为黄土不同冻融次数下的抗拉强度的衰减率变量。由于黄土在含水量19%时的抗拉强度冻融衰减率与其他含水量下有较大差异,故将含水量19%时单独考虑。

综合整理[联立式(3)、(4)、(5)]可得不同含水量(不包括含水量≥19%)以及不同干密度条件下黄土经历n(n≥1)次冻融循环后的抗拉强度值可表示为:

(6)

含水量为19%时,不同干密度条件下黄土经历n次冻融循环后的抗拉强度值可表示为:

(7)

3 讨论

黄土是一种具有结构性与水敏感性的特殊土,此次研究所取黄土试样具有不同孔隙比与饱和度,理论上对于含水量在塑限以下,其冻融过程中水分对结构甚至颗粒的影响不大,即不会对抗拉强度产生较大影响。但是试验结果显示,干密度为1.55 g·cm-3含水量11%和13%及干密度1.60 g·cm-3含水量11%条件下试样在冻融一次时抗拉强度最高,在经历三次冻融循环时抗拉强度减小至最低值。可能原因是初始干密度较小及含水量较小情况下颗粒间排列较为疏松,空隙较大,在经历第一次冻结过程中,由于冻胀破坏了初始团簇大颗粒黏结状态从而在冻结过程中破碎,变成相对较小的颗粒,在融化过程中相对较小的颗粒位置发生变化填充了原本较大的空隙,使得颗粒与颗粒接触数目增多,黏结增强,故在经历一次冻融后强度呈增大趋势,具体原因尚需补充一次冻融过程中土体微观颗粒状态及孔隙特征加以证明。而后的冻融过程中,其抗拉强度具有较为明显的衰减作用,究其原因可能与其冻融过程伴随颗粒间水分迁移与胀缩有关。已有研究表明[11-12],冻融作用可引起非饱和黄土黏粒含量增多,小孔隙减少,大孔隙增多,说明非饱和黄土在冻融过程中结构发生了破坏,是引起抗拉强度衰减的主要原因。然而,结构的破坏有可能是在冻结过程中水分向小孔隙处迁移集中(大孔隙处由于水分不足以填充产生的冻胀力弱)由冻胀力引起,也有可能在融化过程中水分集中融化弱化了颗粒之间的黏结致使抗拉强度降低,或是两者对抗拉强度的衰减均有贡献,这是个值得探讨的问题。对于含水量高(19%)其衰减率高的问题,有可能是因为其初始抗拉强度更低,相对衰减率就更高,实际上冻融作用对高含水量黄土的抗拉强度影响更小,如果用相对强度衰减率来表征黄土的冻融衰减程度,则高含水量(>17%)与低含水量(≤17)黄土不建议采用同一套标准来衡量,此次研究仅仅提供了19%的高含水量样品,数据相对较少,下一步计划补充饱和黄土的冻融循环强度试验,来完善高含水量条件下的冻融强度衰减模型。图8中的数据为每种含水量下不同干密度每次冻融之后强度衰减率的平均值,所拟合出的曲线方程体现了黄土抗拉强度冻融衰减特性的一般规律,旨在说明拟合参数及方程对于兰州及其周边黄土具有一定适用性,是否对于其他地区黄土具有适用性或者对公式进行修正后是否对黄土抗拉强度冻融衰减规律具有普适性尚需进一步研究(用其他地区不同性质的黄土抗拉强度冻融试验结果加以验证)。另外,黄土边坡剥落病害是由于边坡表层黄土冻融作用引起,其剥落机理不仅仅是由于抗剪强度弱化不足引起,与其抗拉强度的弱化也有关系,应该由拉-剪耦合强度破坏准则去解释更为合理,故笔者在已有研究的基础上,计划下一步进行黄土冻融拉-剪耦合强度破坏准则的研究工作。

4 结论

此次黄土抗拉强度冻融特性及衰减模型的研究工作是在多组试验数据的基础上探索其规律的普遍性同时发现其特殊性,得出如下结论:

(1) 对于文中在低干密度、低含水量的情况下(如干密度为1.55 g·cm-3含水量11%和13%及干密度1.60 g·cm-3含水量11%),试样在冻融一次时抗拉强度最高,而后冻融过程抗拉强度减小至最低值,说明抗拉强度随冻融循环次数并不完全呈现衰减特性。但是,从整体趋势上而言,黄土抗拉强度均随冻融循环次数的增加呈指数衰减,其中,冻融3～5次达到衰减程度的稳定值。含水量越大或者干密度越小,冻融作用对其强度值的影响越小,但是对其强度衰减率的影响越大。

(2) 黄土抗拉强度的衰减率随冻融循环次数的增加呈指数衰减关系一般在3次冻融作用后强度衰减率达到最大值。其中,含水量在11%至17%之间时的最终强度衰减量均在15%～30%之间,而含水量19%时的最终强度衰减量可达50%,这说明高含水量黄土的冻融衰减规律具有一定的特殊性。

(3) 在同时考虑黄土抗拉强度冻融规律普遍性与特殊性的基础上,提出了适用于估算兰州黄土抗拉强度的冻融衰减模型。