高烈度区深水斜拉桥动水效应及抗震体系研究

樊 冰,李永庆,宋松林,安艳涛

(中交第一公路勘察设计研究院有限公司,陕西 西安 710075)

0 引言

随着国家西部高速公路网的不断完善,西南山区桥梁建设取得快速发展,出现了较多的库区深水斜拉桥。受地壳板块活动的影响,西南山区为高烈度区,位于此间的深水斜拉桥在地震下,一方面会直接受到地震动作用,另一方面桥墩还会受到附近水体的作用。因此,充分认识动水对斜拉桥结构各部分的影响,对于深水斜拉桥结构的抗震设计非常重要。

国内外学者很早就关注到桥梁结构的动水力,对其计算方法进行了一定研究。Savage[1]于1939年通过pit-river大桥振动台模拟试验,获得了柱状结构桥墩上水体的等效附加质量的解析解。基于线性辐射波浪法,Goto等[2]分析了水平地震作用下齐水面圆截面和椭圆截面弹性桥墩上的动水压力，并给出了解析解。赖伟等[3]得到了矩形空心桥墩内部和外部水体作用于桥墩有限节点上的动水力的解析解。这类解析法偏于理论研究,很难直接用于解决深水斜拉桥这样复杂的工程问题。伴随科技进步,利用有限元的数值法被学者用于计算动水作用。李璐璐等[4]采用CFD方法,在FLUENT中运用边界造波法进行造波,数值模拟波浪作用下斜拉桥单塔结构的桩和承台上的动水压力并验证了其准确性。虽然数值法计算精度高,但是对计算软件要求也较高,且计算模型比较复杂。自Morison等[5]于1950年基于小直径垂直柱体提出从海底直至自由水表面的水平波浪公式,即著名的Morison方程,以此为基础的附加质量法被广泛研究,现在已被纳入欧洲规范和国内公路桥梁抗震设计规范[6]。学者们主要基于此方法对深水斜拉桥结构的动水作用进行了研究。李悦等[7]分析了动水对斜拉桥动力特性及地震反应的影响。高大峰等[8]分析了动水及桩土效应对斜拉桥结构动力特性和地震反应的影响。殷旭东等[9]研究了动水对于墩-塔-梁固结体系斜拉桥抗震性能的影响。林曾等[10]分析了动水压力对多塔斜拉桥墩身内力反应的影响及不同地震波作用下水位对多塔斜拉桥地震响应的影响。现有的研究均表明动水会增大斜拉桥的结构周期,桥塔、桥墩等内力和位移响应也会有所增加。但是学者们对于动水对斜拉桥结构的作用多基于同一级别的地震动,而桥梁抗震设计中需考虑各级地震的作用,因此有必要对斜拉桥结构的动水效应随地震强度的变化做进一步研究。

与一般斜拉桥相比,由于地震荷载及动水的共同作用,结构动力响应大,深水斜拉桥对抗震设计的要求更高,合理的抗震体系有助于提高其抗震性能。目前斜拉桥可采用的纵、横向减震体系较多,各类阻尼器、减隔震装置都有在抗震设计中使用[11],但是是否适用于深水斜拉桥结构,需要进行深入研究。

本文采用附加质量法,参照公路桥梁抗震设计规范法考虑动水作用,以双河特大桥为工程实例,分析斜拉桥结构地震响应受动水作用的影响及其随地震强度的变化特点;在此基础上对大桥合理的抗震体系展开研究,通过对比分析给出抗震性能最好的约束体系,为高烈度区深水斜拉桥的抗震设计提供借鉴。

1 工程概况

双河特大桥为高低塔双索面组合梁斜拉桥,跨径布置为(56+152+356+140) m。主梁采用工字型组合梁,梁高2.8 m,桥面宽28.7 m。桥塔采用高低塔,2#索塔高229 m,3#索塔高170 m。桥塔下塔柱以上及横梁均采用矩形空心截面,下塔墩采用单箱多室截面,下接承台及直径3.5 m的群桩基础。1#辅助墩为双柱式空心薄壁墩,两个桥墩之间通过墩顶系梁连接。每个桥墩下接承台及4根直径2.5 m的群桩基础。桥台均为采用坐板式,下接承台及直径1.8 m、成梅花形布置的群桩基础。

桥塔处水位随白鹤滩水电站水位变动,分死水位、限制水位和蓄水位,蓄水位下2#、3#索塔下塔墩入水深度分别为71.589 m、30.089 m。

大桥位于金沙江的支流河谷区,地层总体较单一,覆盖层厚度变化较大,下卧基岩主要为强风化、中风化玄武岩。桥址区属于II类场地,地震基本烈度为Ⅷ度,地震动峰值加速度为0.20g。

图1 双河特大桥立面布置(单位:m)Fig.1 Elevation layout of Shuanghe super large bridge (Unit:m)

2 动力模型

2.1 有限元模型建立

采用有限元软件Midas/civil建立全桥空间动力模型,如图2所示。根据结构特点,桥塔、主梁、桥墩、桥台及基础均采用梁单元模拟,斜拉索采用桁架单元模拟,文中所涉及的支座采用弹性连接和一般连接模拟。计算中考虑土体的作用,利用“m”法计算土弹簧刚度值,以节点弹性支撑来模拟桩土效应[8,12]。按照蓄水位考虑动水作用,采用附加质量法计算动水压力,对索塔下塔墩入水部分分别计算内外域水质量,将总的附加质量以节点质量的形式添加在动力模型中。

图2 动力模型Fig.2 Dynamic model

2.2 地震动输入

根据双河特大桥《地震安全性评价工作报告》,选用50年超越概率63%(小震)、10%(中震)、2%(大震)各三条时程波,地震峰值加速度分别为0.976 m/s2、2.68 m/s2、4.56 m/s2,图3为其中的一条时程波。计算中考虑竖向地震力的作用,沿顺桥向(以下简称纵向)和横桥向(以下简称横向)分别输入地震动:①纵向+0.6竖向,②横向+0.6竖向,地震响应结果取三条波的最大值。

图3 水平地震加速度时程曲线Fig.3 Time history curve of horizontal seismic acceleration

3 动水效应研究

斜拉桥地震响应与结构支承体系密切相关,为排除抗震体系对结构动水效应的影响,此处计算采用常规约束边界:纵向采用半飘浮体系,仅在索塔处设置竖向约束;横向仅在索塔处设置水平约束。模型中分别输入小震、中震、大震级别的地震波进行时程分析。为方便研究动水对结构响应的作用,引入动水系数η:

各级地震下,结构内力、位移响应的η变化情况如图4所示。

图4 地震下结构内力及位移动水系数Fig.4 Hydrodynamic coefficient of structural internal force and structural displacement under earthquake

由图4(a)可以看到,索塔塔底纵、横向弯矩和剪力的η均大于1,可见不同级别的地震作用下动水都会增大索塔内力响应。纵向地震下,2#索塔塔底弯矩的η>1.5,3#索塔塔底弯矩的η位于1.3～1.5之间,这是因为2#索塔更高,且塔墩入水范围更大,受动水影响更明显。随着纵向地震力增加,3#索塔塔底弯矩的η逐步增加,而2#索塔塔底弯矩的η先增大后减小,且大震下的动水系数要小于小震;两个索塔塔底剪力的η则出现不同程度的先减小后增大,大震下3#塔塔底剪力的动水系数甚至大于2#塔。横向小震下,2#塔塔底弯矩的η小于3#塔,但是横向中震和大震下均比3#塔大,这表明动水对高低塔塔底横向弯矩的影响不仅与结构入水深度相关,也与地震强度有关。2#塔塔底弯矩的η随横向地震力增加呈现较大幅度的先增大后减小,而3#塔塔底弯矩的η则小幅先减小后增大。与弯矩不同,塔底横向剪力的动水系数依然表现为:2#塔>3#塔,且随地震水平提高,均先减小后增大,只是3#塔的增减幅更大。从数值上看,不同地震力下,两个索塔塔底剪力的动水系数均比弯矩的大,尤其在纵向地震下剪力受动水的影响明显大于弯矩,因此设计中应当重点关注索塔的抗剪性能。

由图4(b)可知,考虑动水后结构纵、横向的位移响应也会增加,但是增幅较内力响应小,η=1.04～1.16。两个索塔塔顶位移的动水系数接近,可见高低塔结构形式、结构入水深度等对塔顶位移的动水效应不会产生显著影响。由于纵向采用半飘浮约束体系,大、小桩号梁端纵向位移同步,所以其动水系数也基本相同。随地震强度增加,2#索塔塔顶纵向位移的η先减小后增大,横向位移的η则先增大后减小;3#塔顶纵向位移的η逐渐增加,而横向位移的η先减小后增大;所有位移响应的动水系数增、减幅均很小。纵横向梁端位移的η随地震强度增加呈现相反的变化:纵向梁端位移的η逐渐减小,而横向梁端位移的η逐渐增大,增减幅同样都很小。

以上分析表明,地震下动水作用会显著增大索塔塔底内力尤其是剪力响应,也会使塔顶、梁端位移小幅增加。动水对结构动力响应的放大作用不会因为地震强度变化产生质的改变,但是会发生量的变化。随地震力增加,各内力、位移响应的动水系数增减趋势不一。这是因为结构地震响应不仅与地震动峰值加速度有关,也与加速度时程的频谱特性有关。从表1可以看出,各级地震时程波对应的加速度反应谱的特征周期不同,因而结构各内力和位移响应随着地震强度增加不会线性增加。考虑动水作用后,结构动力特性发生变化,自振周期增大,结构各响应在各级地震下又会产生不同的变化,所以结构各内力、位移响应的动水系数随地震强度增大并没有呈现出明显的变化规律。因此在进行深水斜拉桥抗震设计时,各级地震下应分别考虑动水作用,若采用相同的动水系数计算地震响应,将会造成结构尺寸设计不合理,引发安全隐患。

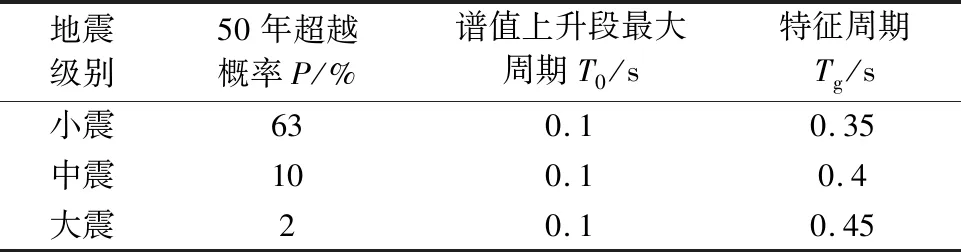
表1 加速度反应谱参数Table1 Acceleration response spectrum parameters

4 抗震体系研究

在前述常规约束体系下,大震中大桥结构响应如图5所示。可以看出,主梁梁端和塔顶都发生了较大位移,索塔塔底也产生了很大的弯矩和剪力,且数值远大于辅助墩。考虑动水作用后,索塔内力及结构位移进一步增大。显然,对于高烈度区深水斜拉桥,常规约束体系已不能满足抗震要求,有必要对其动力约束体系进行研究以确定合理的抗震体系。

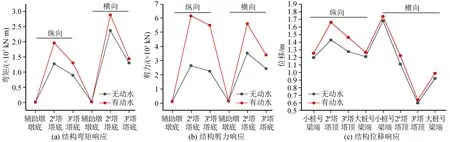
图5 大震下结构响应Fig.5 Structural response under large earthquakes

4.1 纵向抗震体系

目前斜拉桥应用较多的纵向减震体系主要有阻尼体系、弹性约束体系或二者组合使用[11,13-16]。为减小索塔地震响应,多将减震约束设置在塔梁结合处(索塔减震体系),其中减震效果较好的是采用阻尼体系[14,16]。对于深水斜拉桥,由于动水的放大作用,索塔内力增加最为显著。为更有效降低索塔内力响应,抑制结构位移,应充分发挥辅助墩和桥台的抗震能力。

基于以上分析,提出“协同减震体系”:在桥塔处设置阻尼约束,在桥台、辅助墩处采用弹性约束或阻尼约束,让所有下部结构均参与抗震。弹性约束的典型代表是弹性限位索,静力下不影响结构正常运营,动力荷载作用下依靠弹性索变形起到限位作用;减震效果最佳的阻尼约束是黏滞阻尼器,静力下对结构内力不产生影响,地震下通过黏滞流体阻尼耗能。二者的力学模型及参数如图6所示,图中k为弹性索的刚度;c为黏滞阻尼器的阻尼系数;α为阻尼指数。

图6 力学模型Fig.6 Mechanical model

为检验“协同减震体系”的抗震效果,进一步确定辅助墩及桥台位置合理的约束形式,建立两种具体的支承布置,并与半飘浮体系、索塔减震体系进行对比。四种纵向约束体系的支座设置及参数列于表2。

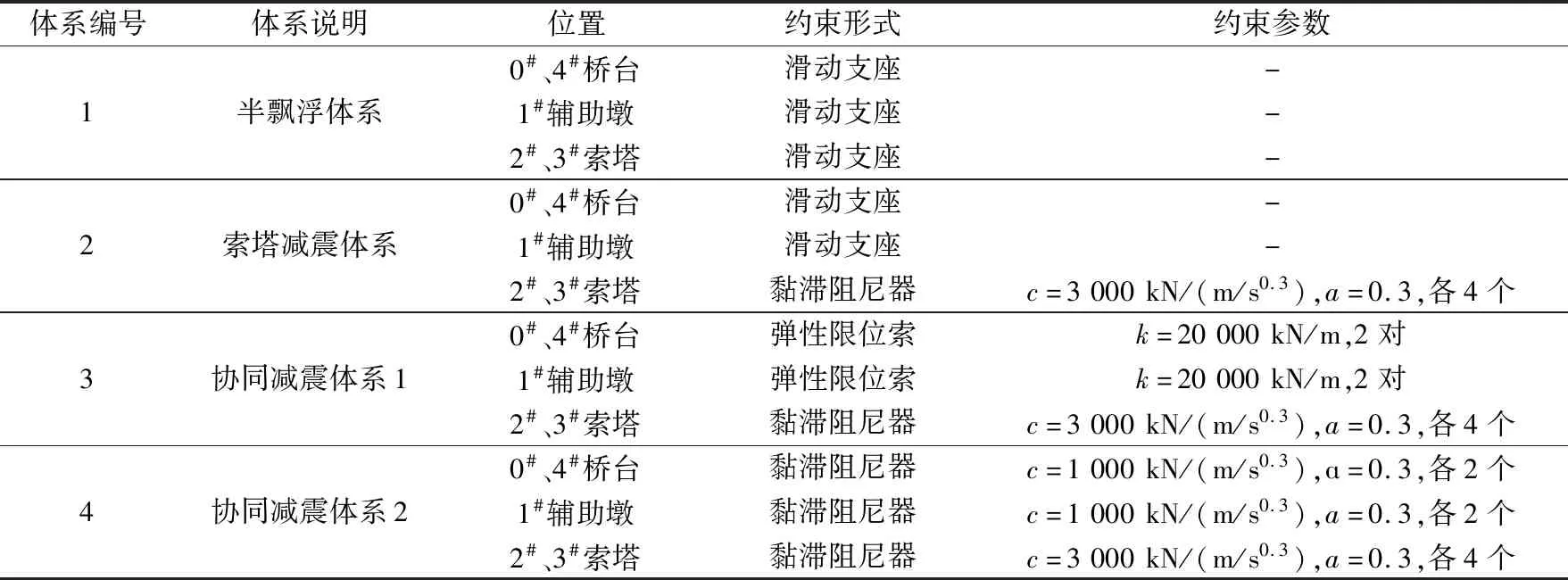
表2 纵向抗震体系比较表Table 2 Comparison of longitudinal seismic systems

4.2 横向抗震体系

为提高结构整体的抗震性能,斜拉桥横向也多采用协同抗震理念,在主梁与塔、墩、台连接处都设置一定约束。具体的约束形式有固定约束、弹塑性约束、弹性约束及组合约束[11,17-18]。固定约束体系往往在桥塔处设置抗风支座实现横向限位[11],其余位置采用固定支座。弹塑性约束分弹塑性钢支座和一般球钢支座+弹塑性钢阻尼装置组合体系两种(力学模型见图7),二者本质上是相同的:既满足正常运营支座位移的需要,又能依靠钢材料的弹塑性变形在地震中耗能,利用恢复力实现限位功能。组合约束将各约束体系交叉使用,最常见的是在索塔采用固定约束,其余位置设置弹性或弹塑性约束。

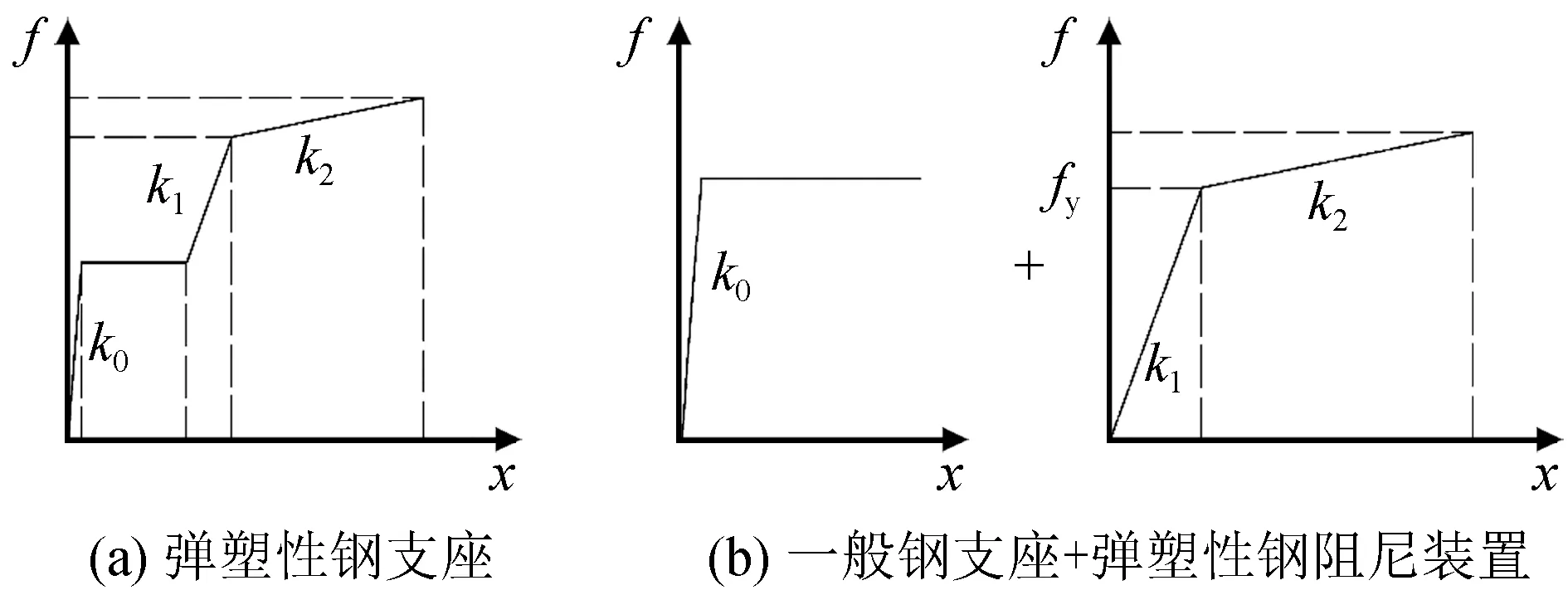
图7 弹塑性约束力学模型Fig.7 Mechanical model with elastoplastic constraints

本文对这几种横向约束体系分别展开研究,并与常规约束体系进行对比分析,以选出最好的抗震体系。具体工况设置及相关参数列于表3。

表3 横向抗震体系比较表Table 3 Comparison of transverse seismic systems

5 减震效果分析

首先对采用上述纵、横向抗震体系的计算模型进行特征值分析,考察结构的动力特性;然后输入大震级别的地震波,进行非线性时程分析,比较强震下结构的地震响应。各体系的纵、横向动力响应指标均以体系1为基准,以减震率γ反映减震效果:

5.1 动力特性比较

纵向抗震体系下结构的纵向振型在低阶模态变化较大,前三阶模态列于表4。可以看出,体系1～体系3的模态特征完全相同,这是由于黏滞阻尼器在工作中不会增加附加刚度,对结构的动力特性没有影响。体系4较体系1,由于弹性限位索的约束,结构纵向刚度增加,一阶振型由主梁纵飘变为主梁竖弯,周期大幅减小,2、3模态对应的周期也相应减小。

表4 结构纵向典型模态Table 4 Typical longitudinal mode of structure

表5列出了各横向抗震体系下结构前三阶模态。可以看出,由于主梁在辅助墩和桥台处缺少约束,体系1首先出现主梁横弯模态。其余体系中主梁存在横向约束,结构横向刚度变大,一阶振型均为主塔横弯。体系3～体系6中主梁横向约束减弱,结构刚度减小,所以横向一阶振型的周期比体系2的大。在组合体系5、6中,由于塔梁处约束加强,结构整体横向刚度增大,因而振型周期较体系3和体系4小。

表5 结构横向典型模态Table 5 Typical transverse mode of structure

5.2 纵向减震比较

图8给出了各纵向抗震体系的结构响应的减震率。

由图8(a)可以看出,体系2～体系4的索塔塔底弯矩和剪力的γ均大于10%,这表明索塔减震体系和协同减震体系都能显著减小索塔内力响应。对于塔底弯矩,体系4的减震率最大,体系3最小,体系2介于二者之间,而对于2#塔塔底剪力,体系3的减震率最大,体系2和体系4基本相同;3个体系的3#塔塔底剪力减震率非常接近。可见,协同减震体系均采用黏滞阻尼器的方案对塔底弯矩的减震作用最好,弹性限位索+黏滞阻尼器的方案对减小塔底剪力效果最佳。

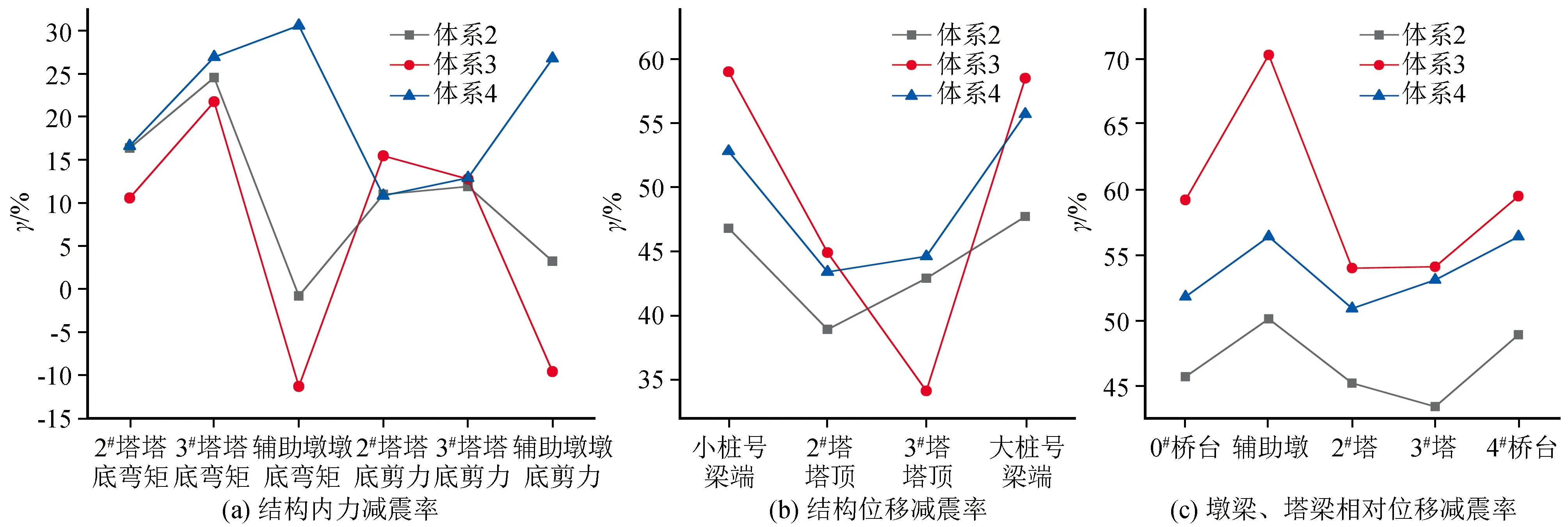
图8 纵向抗震体系结构响应减震率比较Fig.8 Comparison between damping ratios of structural responses with longitudinal seismic system

对于辅助墩墩底弯矩和剪力,体系4的γ均大于25%,体系2的γ位于0附近,体系3的γ小于0,这表明与半飘浮体系相比,索塔减震体系几乎不会改变辅助墩内力,而协同减震体系对辅助墩内力影响较大:均采用黏滞阻尼器方案可以有效减小辅助墩墩底内力,弹性限位索+黏滞阻尼器的方案则会增大辅助墩墩底内力。

由图8(b)可知,体系2～体系4在地震下均可以有效抑制主梁位移,梁端位移的减震率均达45%以上,其中体系3的限位作用最好,体系4次之。索塔塔顶位移在体系2～体系4中也大幅下降,对于2#塔,减震率:体系3>体系4>体系2;对于3#塔,则是体系4的减震率最大,体系3最小。这是因为3#索塔与4#桥台间未设置辅助墩,相较于2#索塔,由于缺少弹性索限位,索塔附近主梁位移减小量就少,经由斜拉索传递至索塔引起塔顶位移的减幅也相应减少。

图8(c)表明,体系2～体系4较体系1各支承位置主梁的相对位移明显减小,结合2#索塔及辅助墩处的阻尼器力-位移曲线(图9,篇幅有限,仅给出位移响应最大的时程波对应的滞回曲线),可以看到三个体系中阻尼器的滞回曲线饱满,均发挥了良好的耗能和限位作用。比较各体系主梁相对位移减震率,体系3大于54%,体系2达43%以上,体系4居于二者之间。可见,协同减震体系能够更好地控制结构位移响应,其中弹性限位索+黏滞阻尼器的方案限位效果最好。

图9 黏滞阻尼器的力-位移曲线Fig.9 Force-displacement curve of viscous damper

综合上述分析,与索塔减震体系相比,本文提出的协同减震体系在减小结构位移响应,尤其是支承位置主梁相对位移方面具有明显的优势,但是在控制结构内力上取决于非索塔支承位置采用的约束体系。辅助墩、桥台处均设置弹性限位索的方案会引起辅助墩内力增加,对索塔弯矩的减震作用也一般;而辅助墩、桥台处均设置黏滞阻尼器的方案能同时大幅降低结构内力和位移响应,显著提升结构整体的纵向抗震性能。

5.3 横向减震比较

各横向抗震体系下,结构响应的减震率如图10所示。从图10(a)中可以看出,体系2中只有2#索塔塔底弯矩的γ稍大于0,体系3中只有辅助墩墩底弯矩和剪力的γ大于0,这表明固结约束体系和弹性约束体系不能降低地震下结构整体内力响应,因而不宜在高烈度区斜拉桥横向抗震设计中使用。

图10 横向抗震体系结构响应减震率比较Fig.10 Comparison between damping ratios of structural responses with transverse seismic system

体系4中除了塔底剪力的γ小于0外,其余内力响应的γ均位于10%以上。体系5中各内力响应变化都很小。体系6中所有内力响应的γ>0,其中索塔塔底和辅助墩墩底弯矩的γ约为体系4的一半。因此只有体系6能够降低结构所有内力响应,体系4可以最大幅度减小索塔塔底弯矩和辅助墩墩底内力,但是会使索塔塔塔底剪力增加。

图10(b)中,体系2～体系6的小桩号梁端位移的γ均大于70%,大桩号梁端位移的γ均大于35%,减震率最高的前三个体系依次为体系2、体系4和体系6。对于索塔塔顶位移,体系4的γ最大,其次为体系6,其余体系中都存在γ<0的情况。图10(c)中,由于塔梁处采用了固定约束,体系2、体系5和体系6中塔梁间没有相对位移。体系3和体系4中索塔处支座发生了0.27～0.35 m的位移,体系4中非索塔位置的主梁相对位移最小,其次为体系6。由图11(篇幅有限,仅给出位移响应最大的时程波对应的滞回曲线)可以看出,体系4和体系6中辅助墩及2#索塔位置的钢阻尼器在大震下均进入了塑性变形阶段,起到了耗能和限位的作用。

图11 钢阻尼器的力-位移曲线Fig.11 Force-displacement curve of steel damper

总体来看,在所有横向抗震体系中,体系4和体系6的减震效果较好,在控制结构地震响应上各具优势。体系4能够最有效地降低索塔塔底和辅助墩墩底弯矩、塔顶和梁端位移及非索塔处的主梁相对位移,但是对索塔处主梁限位效果一般,同时会引起塔底剪力小幅增加;而体系6在较好控制结构整体位移的基础上可以同步降低索塔内力和辅助墩内力。

5.4 推荐抗震体系

根据以上分析,综合考虑各纵、横向抗震体系的整体抗震表现,以同时减小结构内力和位移响应为评判标准,针对强震区深水斜拉桥的合理抗震体系提出以下建议:(1)纵向抗震体系采用设置阻尼约束的协同减震体系,在索塔、辅助墩及桥台处均设置黏滞阻尼器;(2)横向抗震体系采用组合约束体系,在辅助墩及桥台处设置横向钢阻尼器等弹塑性约束,在索塔处设置横向固定约束。

6 结语

本文以双河特大桥为背景,对高烈度区深水斜拉桥的动水效应及纵、横向合理的抗震体系进行了研究,得出以下结论:

(1) 地震下动水作用不仅会显著增大索塔塔底内力尤其是剪力响应,还会小幅增加索塔塔顶和主梁梁端的位移。

(2) 斜拉桥结构的动水效应与地震强度密切相关,随地震力增加,结构各内力、位移响应的动水系数增减趋势不一,没有明显规律。在进行抗震设计时,应对各级地震下的动水作用分别计算。

(3) 纵向采用协同减震体系相比常见的索塔减震体系能显著降低结构纵向位移响应。结构纵向抗震体系推荐采用在索塔、辅助墩和桥台处均设置黏滞阻尼器的协同减震体系,该方案能最有效降低结构内力及位移响应,提升结构整体的纵向抗震性能。

(4) 结构横向抗震体系推荐采用在辅助墩、桥台处均设置钢阻尼器+索塔处设置固定约束的组合体系,该体系在较好控制结构整体位移的基础上能同时降低索塔内力和辅助墩内力,提升结构整体的横向抗震性能。

(5) 本文针对高烈度区深水斜拉桥提出的合理抗震体系中建议采用的黏滞阻尼器、钢阻尼器等弹塑性装置的具体力学参数应当结合应用桥梁的实际情况计算确定。