基于UKF的联合信道参数估计和数据检测算法

潘基翔

(安徽邮电职业技术学院，安徽 合肥 230031)

正交频分复用(OFDM)技术是一种使用在无线环境下的高速多载波传输技术，应用于4G、5G和高速无线局域网等需要高速数据传输的场景。其主要原理是将高速串行数据转换成低速并行数据进行传输。OFDM中并行的正交子信道带宽较小，提高频谱效率的同时也对多径衰落具有抵抗特性，易于均衡，可提升系统的传输性能。

由于OFDM的技术特征，如果能够对无线信道进行更加精确的估算，就可以更好地提升其性能指标。针对OFDM系统，学者们提出了基于导频的信道估计[1-2]、盲信道估计、半盲信道估计等多种算法。基于导频的信道估计是OFDM系统的主流估计方式，它通过周期性地在数据信号中插入导频信号，以测量并追踪导频信号的变化对导频信道进行估计，再进一步估算数据信道。该算法对导频的发射频次具有依赖性，频次不足影响估算结果，频次过高又会影响系统传输效率[3]。盲信道估计[4-5]能够在不借助任何外加信息的基础上获取信道特性，但需要对接收的数据信息进行统计分析，不适合快速变化信道的估计，收敛速度慢。有文献提出半盲信道估计算法[5-6]，结合以上2类算法的特点，在盲信道估计算法中加入少量的导频信号，提高了算法的计算效率。本研究提出在算法中使用无迹卡尔曼滤波(UKF)的方法，可以在少量导频和先验信息有限的条件下对信道的真实状态进行估计。该算法的特点是在联合信道参数聚集和数据监测算法的基础上，每次迭代都对信道冲击响应和噪声方差的估计值进行更新。仿真结果表明，该算法在导频数量较少的情况下仍然具有较好的表现，迭代次数变化不大。同时，本方法比使用相同导频量的内插值算法[10]有更好的收敛特性。

1 OFDM系统数据模型

增加导频和信道估计部分之后的OFDM系统的运行流程如图1所示。

图1 加入导频符号和信道估计的基带OFDM系统流程图Fig.1 Block diagram of baseband OFDM system with pilot symbols and channel estimation

在本研究中，假设：

(1)循环前缀长度大于信道冲激响应长度。

(2)接收机和发射机不存在失步的情况。

(3)传输信道具有准静止的特性，信道特性在1个OFDM符号的时间范围内不会变化。

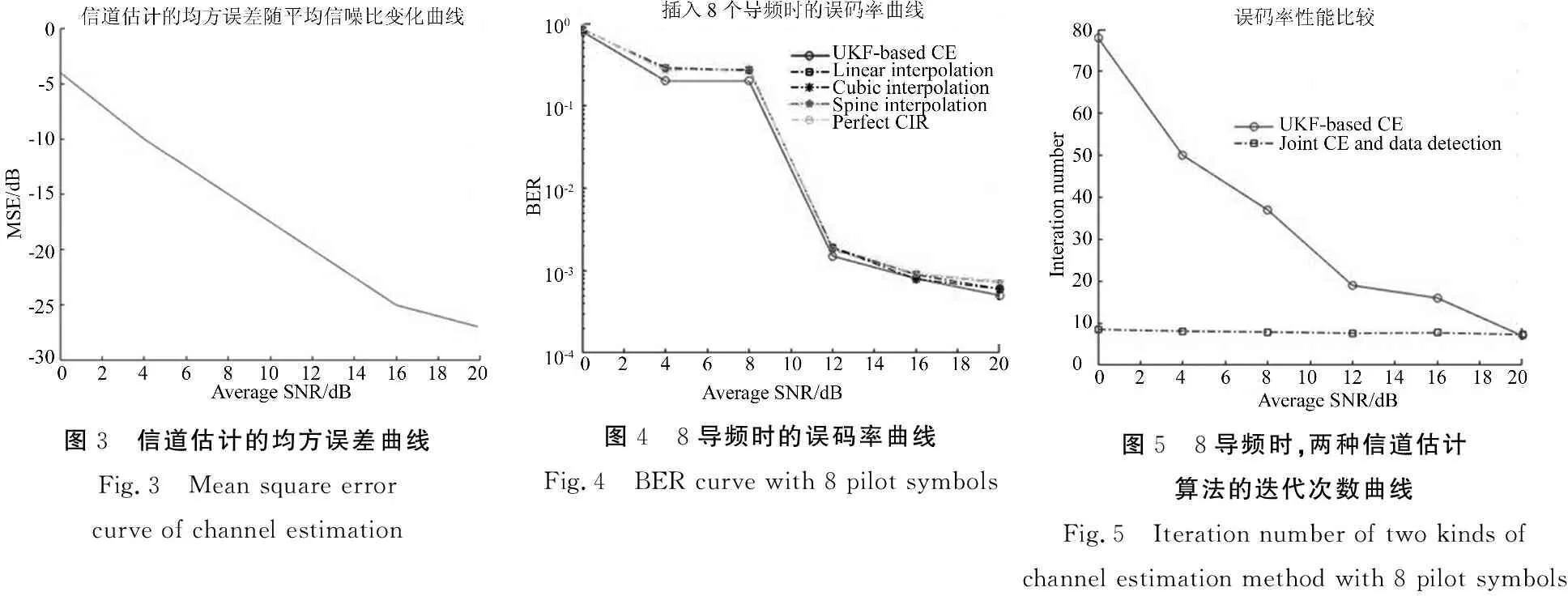
在图1的数据传输过程中，假定系统中发射和接收的子载波数量为N，以此构建频域发送的数据流符号向量N×1阶向量Sn和接收的数据流符号向量N×1阶向量Yn；其中，有少量子载波是用于传输导频符号的，假设这部分子载波数量为M(显然，M

在某一时刻n，OFDM传输系统表示为接收的数据符号向量Yn与发射的符号向量Sn之间的函数：

Yn(k)=Sn(k)Hn(k)+Wn(k),k=0,1,…,N-1

(1)

其矩阵形式为：

简记为：

Yn=Diag(Sn)Hn+Wn

(2)

根据假设条件(3)，且假定每次信道估计都可以在一个OFDM符号之内完成，则可以省略式(1)中下标n，将其改写为如下形式：

Y=Diag(S)H+W=Diag(S)FLh+W

(3)

以k(k=0,1,…N-1)作为子载波的编号，第k个子载波上的衰落系数用H(k)表示：

其中h=[(h(0)h(1) … (h(L-1)]T代表信道特性的冲激响应函数，L是信道冲激响应长度。

FL是去掉N-L列的N点离散傅里叶变换阵的子矩阵，其元素为：

插入数据中的导频通常是等间隔形式的，设间隔为Df，一个完整的OFDM发送符号S表示为：

(4)

m=0,1…,M-1

这里k=mDf+l=0,1,…,N-1。

如果对式(1)进行进一步分析，可以发现OFDM对数据符号流的处理可以用图 2 进行标识。OFDM系统中的数据传输是由并行并且相互独立的N个窄带子信道完成的。其信道特性是子信道的特性的相互叠加。

图2 并行的子信道 Fig.2 Parallel sub channels

因为不同的子信道特性是相互独立的，接收的数据流符号与发射数据流符号、子信道特性、信道噪声之间的关系可以用如下的复高斯分布表示：

(5)

2 基于无迹卡尔曼滤波(UKF)的信道估计算法

首先设定好信道估计中用到的σ采样点均值和方差的各自权重。计量过程如式(6)

(6)

σ(k│k-1)=F(σi-1,Uk-1)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

3 仿真参数及结果

3.1 信道模型

在信道模型中，本研究选取多径信道衰落的脉冲激励响应，如式(18)所示。

(18)

在式(18)中，用i代表无线信号在空中经历的不同路径的编号，i=0,1,2…r，假定r代表多径数量的最大值。在第i条路径上，信号的衰落特性用αi(n)表示；由于用户的移动所造成的信号频率偏移量为f(Di)；不同路径长度造成的信号传输时间差用τi来表示；接收系统对信号进行采样的时间间隔是Tn。在整个系统中，多径衰落的幅度变化情况服从Rayleigh分布的。

另外，本研究采用Ma等[8]所提的基于正弦波叠加法的仿真模型以降低计算的复杂度，提高仿真的效率[7]。其特点是对模型中的随机相移进行了确定化，引入了广义非平稳性，且不具备各态历经性。本研究采用6径Jakes信道模型。其该模型使用中具备相互独立的各路径参数，且各个路径的信号幅度具有Rayleigh分布的特征，且相位是均匀分布的[5]。具体参数赋值获取如表1所示。

表1 信道参数Table 1 Channel parameters

3.2 系统参数

本研究仿真中设计的系统参数包括：传输数据的频率范围是2 MHz，划分成64个子载波，在传输中采用的调制方式是QPSK，并且假定每条路径的最大多普勒频移不超过100 Hz。

3.3 仿真结果与分析

在初次的仿真过程中，导频的插入方式是8导频等间隔插入。随着平均信噪比的增加，算法的均方误差逐渐缩小，图3证明了算法具备收敛性质，最终能够计算出给定的信道参数。仿真中也比较了不同信道估计算法的性能，图4中包含基于UKF的信道估计算法，线性插值法、CUBIC插值法、SPLINE插值法，以及基于UFK的联合信道估计和数据检测算法。随着平均信噪比的增加，在8导频等间隔插入的系统中，这几种算法都有比较好的表现，采用UKF之后的信道估计的计算结果与逼近于信道参数完全已知的理想情况相比差距并不明显。图5比较2种算法的迭代次数随信噪比变化的情况，其中一种是基于UKF的信道参数估计算法，另一种是在UKF的基础上添加联合信道参数估计和数据检测算法，可以看到，后一种算法在低信噪比的条件下，迭代次数有明显的下降；而随着信噪比的增加，2种算法的迭代次数逐渐靠近。

图3 信道估计的均方误差曲线Fig.3 Mean square error curve of channel estimation图4 8导频时的误码率曲线Fig.4 BER curve with 8 pilot symbols 图5 8导频时,两种信道估计算法的迭代次数曲线Fig.5 Iteration number of two kinds of channel estimation method with 8 pilot symbols

图6是将插入导频的数量从8个减少为4个，即减少一半的导频之后，再次对上述几种方法的误码率性能进行比较。可以看到，导频数量减少至一半之后，所有算法的性能都有一定程度的下降，相比较而言，插值方法的性能下降比较明显。图7比较基于UFK的联合信道估计和数据检测算法在8导频和4导频等间隔插入这2种条件下，算法的平均迭代次数。可以看出,导频数量较多时系统的迭代次数较少，次数随平均信噪比的增强而逐渐下降。在图7的结果中，当导频数量从8个变为4个之后，算法的迭代次数大约只需要增加1次。

图7 联合信道估计和数据检测算法平均迭代次数曲线Fig.7 Average iteration number curve of joint CE and data detection algorithm

4 结论

本研究提出的迭代信道估计方法是基于UKF算法的形式实现的，能够很好地跟踪信道的时变特性，同时在导频数量较多的时候，很快收敛到指定参数的信道；在导频数量较少的时候，能够较好保持系统的性能。为改善收敛速度，使用联合信道参数估计和数据监测算法，减少迭代次数。