计及动态冲击挤进过程的埋头式弹药内弹道特性

常人九， 薛晓春， 余永刚

(南京理工大学 能源与动力工程学院， 江苏 南京 210094)

0 引言

弹丸挤进膛线的过程是内弹道全过程中一个重要的阶段，该阶段现象非常复杂，涉及材料弹塑性力学等问题，且经历的时间和行程都非常短，试验难以准确测量。为了简化处理，经典内弹道理论采用瞬时挤进的假设，略去了该过程，不利于完整精确地刻画装药点火燃烧初期阶段的内弹道特性。尤其对于埋头式弹药，由于其采用的是两级点火和火药程序燃烧的新原理，即弹丸缩在药筒内部，在嵌入坡膛之前已经在可燃导向筒内自由滑动了一段距离。因此，一级点火后期，弹丸会以一定初速度动态冲击挤入坡膛，而后在二级点火作用下，弹丸与坡膛产生强摩擦，坡膛内壁不断侵蚀弹带材料，使其发生强变形失效。整个挤进过程具有高瞬时、强冲击和大变形的非线性特点。

目前国内外已针对传统弹丸的挤进过程进行了较多的研究，并取得了一定成果。彭涛等建立了较为简单的弹丸挤进模型，并对弹带挤进的应力变化特性进行了分析。孙河洋等揭示了不同坡膛结构下弹带变形及坡膛裂纹产生的机理。吴斌等提出了一种从摩擦学角度研究弹丸挤进过程的新途径。丁传俊等基于热力耦合有限元模型对弹带挤进过程进行了仿真研究。王鹏等基于Johnson-Cook本构模型分析了摩擦作用对弹丸挤进过程的影响规律。曹学龙等研究了不同弹带宽度对弹丸挤进过程的影响。孙玉杰等基于光滑粒子流体动力学(SPH)-有限元法(FEM)耦合方法对弹丸膛内运动过程进行了分析，提供了一种研究弹带挤进过程的新方法。孙鹏等对不同模块装药条件下弹丸的挤进过程进行了数值模拟，表明了不同装药号对弹带挤进过程的动力学影响机制。梁兴旺等通过弹带受力分析获得了挤进过程中的弹带刻痕形成规律。何行等对不同坡膛锥度对弹带挤进过程的影响进行了仿真研究。苗军等基于某无后座力炮对两种不同材料的弹带挤进过程进行了研究。李加昭数值分析了某制导炮弹的弹带不同过盈量对挤进过程的影响。邹利波等基于温度修正法建立了弹丸挤进过程的摩擦模型，并数值分析了弹带表面温度变化规律。

本文针对某40 mm埋头式弹药，建立埋头式穿甲弹动态冲击挤进的三维有限元模型，基于LS-DYNA软件，数值分析弹丸冲击挤进时期的损伤失效机理及应力、应变特征，并拟合得到挤进阻力的表达式。在此基础上，针对埋头式弹药的特殊结构，建立了埋头式弹药挤进过程初始内弹道与挤进完成后内弹道的一体化精确化模型，考虑埋头式弹丸冲击挤进时期的阻力变化特性，用以修正现有内弹道模型瞬时挤进的假设。

1 埋头式弹药内弹道一体化模型

1.1 埋头式弹药发射过程

图1为埋头式弹药的结构示意图。由图1可知，埋头式弹丸是缩在药筒内部，并通过可燃导向筒对其进行定位，主装药散布在可燃导向筒和传火管四周。当埋头式弹丸发射时，底火击发，产生的高温高压燃气首先通过中心传火管进行一级点火，即点燃速燃药，并推动弹丸在导向筒内自由滑动至弹带前端面接触到坡膛起始部，此时弹丸已经具有了一定的初速度，开始进行挤进过程。与此同时，在一定的压力作用下，可燃导向筒也被压裂、压碎，主装药被全面点燃，进入到二级点火燃烧阶段。随着火药燃气的不断产生，弹带逐渐挤入坡膛，当弹带全部嵌入身管膛线部时挤进过程结束，此时弹带已经被膛线刻出槽，并与膛线紧密贴合。整个挤进过程发生在一级点火后期及二级点火初期，涉及到的受力和变形情况十分复杂，具有强冲击、大变形和高瞬时等特点。

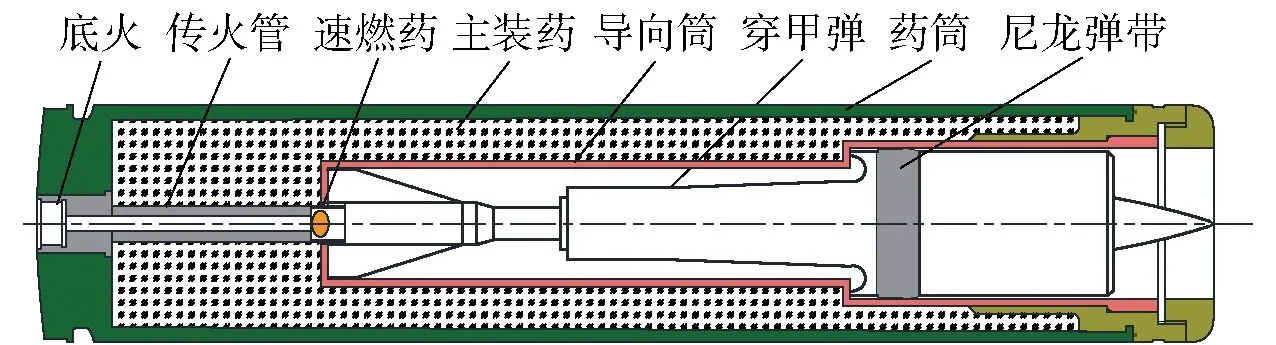
图1 埋头式弹药结构示意图Fig.1 Schematic diagram of the ammunition structure

1.2 考虑动态冲击的内弹道一体化模型

本文在充分考虑埋头式弹药两级点火和火药程序燃烧新原理的基础上，抓住埋头式弹丸射击过程中的主要因素，并考虑其动态冲击挤进特性，将挤进阻力公式耦合到内弹道方程中，构建埋头式弹丸挤进过程初始内弹道与挤进完成后内弹道的一体化精确模型。

1.2.1 一级点火阶段

一级点火阶段，从底火击发到速燃药燃烧，可燃导向筒炸裂前，弹丸在导向筒内近似自由滑动，直至嵌入坡膛。

1)一级速燃药形状函数方程

=(1+)

(1)

式中：为一级速燃药的已燃百分数；、为一级速燃药的形状特征量；为一级速燃药的已燃相对厚度。

2)可燃导向筒形状函数方程

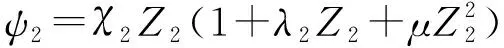
(2)

式中：为可燃导向筒的已燃百分数；、为可燃导向筒的形状特征量；为可燃导向筒的已燃相对厚度；为火药形状特征量。

3)一级速燃药燃烧速率方程

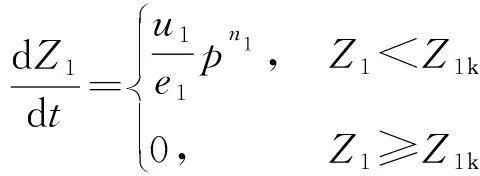
(3)

式中：及分别为速燃药的燃速系数和燃速指数；为一级点火阶段燃烧室内压强；和分别为速燃药弧厚的一半和燃烧结束点的相对弧厚，k为燃烧结束点标示。

4)可燃导向筒燃烧速率方程

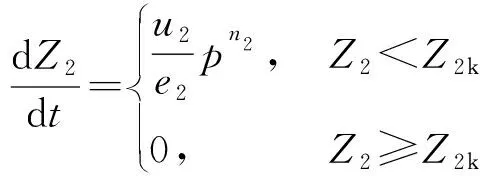
(4)

式中：及分别为可燃导向筒的燃速系数和燃速指数；为一级点火阶段燃烧室内压强；和分别为可燃导向筒壁厚的一半和燃烧结束点相对厚度。

5)弹丸在导向管内速度方程

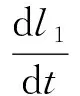
(5)

式中：为一级点火阶段弹丸运动距离；为弹丸运动速度。

6)弹丸在导向管内运动方程

(6)

式中：和分别为埋头式弹丸的最大横截面积和质量；为弹底压力；为一级点火阶段的次要功系数。

7)内弹道能量方程

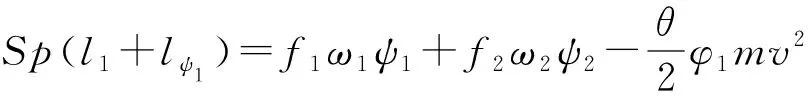
(7)

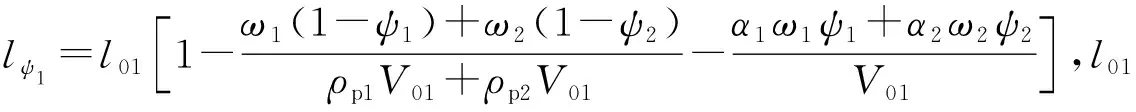
122 二级点火阶段

二级点火阶段，从主装药全面燃烧，到弹丸挤入膛线，并在身管内运动直至飞离炮口。

1)二级点火阶段形状函数方程

(8)

式中：为主装药的已燃百分数；、及为主装药的形状特征量；为主装药的已燃相对厚度；及为主装药分裂点后形状特征量；为主装药燃烧结束点相对弧厚。

2)二级点火阶段燃烧速率方程

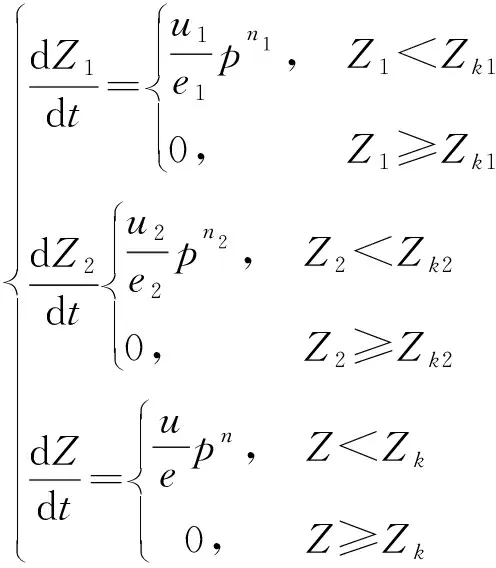
(9)

式中：及分别为主装药的燃速系数和燃速指数；为主装药弧厚的一半。

3)弹丸在身管内速度方程

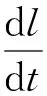
(10)

式中：为二级点火阶段弹丸运动距离。

4)弹丸在身管内运动方程。

冲击挤进时期的弹丸运动方程：

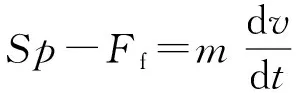
(11)

式中：为弹丸动态冲击挤进阻力，通过第2节冲击挤进的有限元模拟拟合得到。

冲击挤进结束后弹丸运动方程：

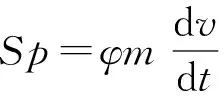
(12)

式中：为二级点火阶段的次要功系数。

5)内弹道能量守恒方程。

冲击挤进时期的能量守恒方程为

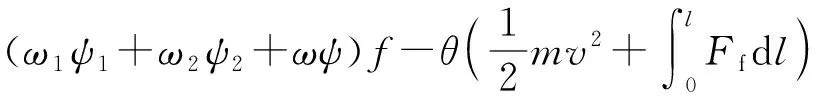
(13)

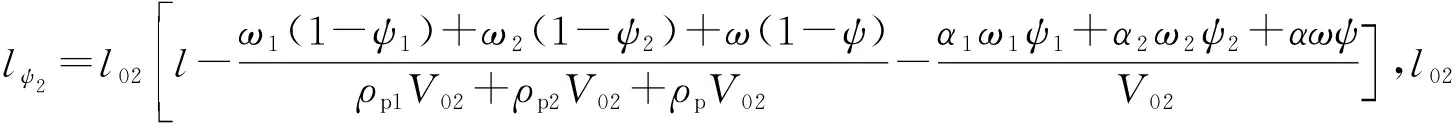
冲击挤进结束后的能量守恒方程为

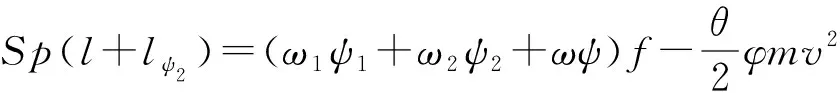
(14)

该方程考虑了弹丸挤进时期的运动摩擦与弹带变形的能量耗散，并用挤进阻力所作的功表示，能更精准地反映其内弹道特性。为得到上述内弹道一体化精确模型中的挤进阻力公式，下面重点对埋头式弹丸的动态冲击挤进过程进行建模并仿真。

2 埋头式弹丸冲击挤进的有限元模型

2.1 基本假设

在考虑埋头式弹丸发射过程主要特点的基础上，提出如下简化假设：

1)由于挤进过程具有高瞬时的特点，持续时间相对于整个内弹道过程而言较短暂，假定挤进过程为绝热冲击过程，不考虑温度应力场，也不考虑弹带与坡膛内壁面摩擦产生的热量等热载荷。

2)弹丸运动所受的运动阻力仅为弹带摩擦阻力和弹带变形产生的阻力。

3)埋头式穿甲弹弹带起始接触坡膛的时刻作为挤进开始时刻，且开始时刻弹带没有初始应力和变形。

4)弹丸在运动过程中始终与身管共轴线，且阻力方向沿身管轴线方向。

5)着重分析弹带挤进运动变形的影响，不考虑身管与弹体的应变，将其假设为刚体，从而减少计算时间。

2.2 有限元网格划分

在进行埋头式穿甲弹挤进系统的建模时，对于身管、弹丸和弹带结构均选择八节点六面体实体网格单元，并在LS-DYNA软件中采用网格扫掠法进行该网格划分。由于弹带是挤进成形的关键部位，对其进行网格加密处理。本文分别建立了01 mm、02 mm和03 mm三种不同网格尺寸的弹带有限元模型，并分别试算，用以网格独立性分析。其分析标准为：若使用细化网格单元与原网格的计算结果相差在5以内，则认为网格密度已达到要求。在进行试算之后，最终选取02 mm作为弹带网格的基本尺寸。由于假设弹体和身管是刚性体，对其建模时选择较大网格尺寸，最终选取弹体和身管的网格尺寸均为05 mm。图2为数值计算最终所采用的弹带和身管有限元网格模型，其中整体模型的网格数量为126 219，弹带部分的网格数量为111 264。由于本节重点研究弹带挤进坡膛的过程，在建立身管模型时采用短身管模型，以减少计算时间。

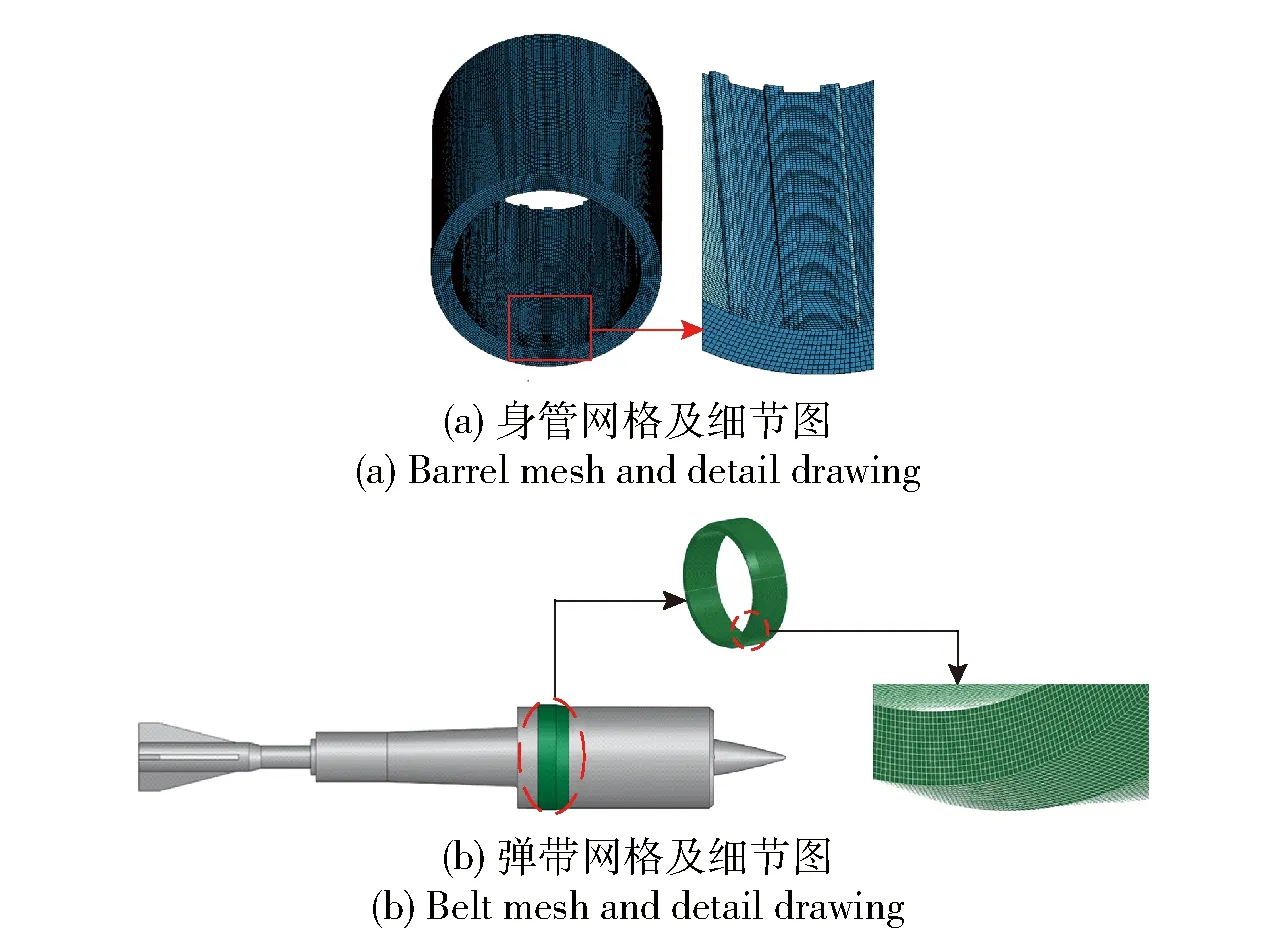
图2 有限元网格模型Fig.2 Finite element mesh model

2.3 材料动态本构模型

埋头式穿甲弹的弹带材料为尼龙，其初始参数如表1所示。身管和弹丸为高强度的炮钢，采用刚体模型对其进行描述，其参数如表2所示。根据尼龙材料的力学性能，在分析中尼龙弹带选择双线性随动塑性材料模型，该模型是各向同性或随动硬化的混合模型，且材料最大塑性失效应变为06，即当材料应变大于06时，判定该处材料失效。通过在仅随动硬化和仅各向随动硬化间调整硬化参数来选择各向同性硬化和随动硬化进行分析，将表1中材料初始参数代入到双线性随动塑性材料模型中，通过显示求解器计算出瞬时过程参数。应变率用Cowper-Symonds模型来进行描述，其屈服应力采用应变率相关因素可表示如下：

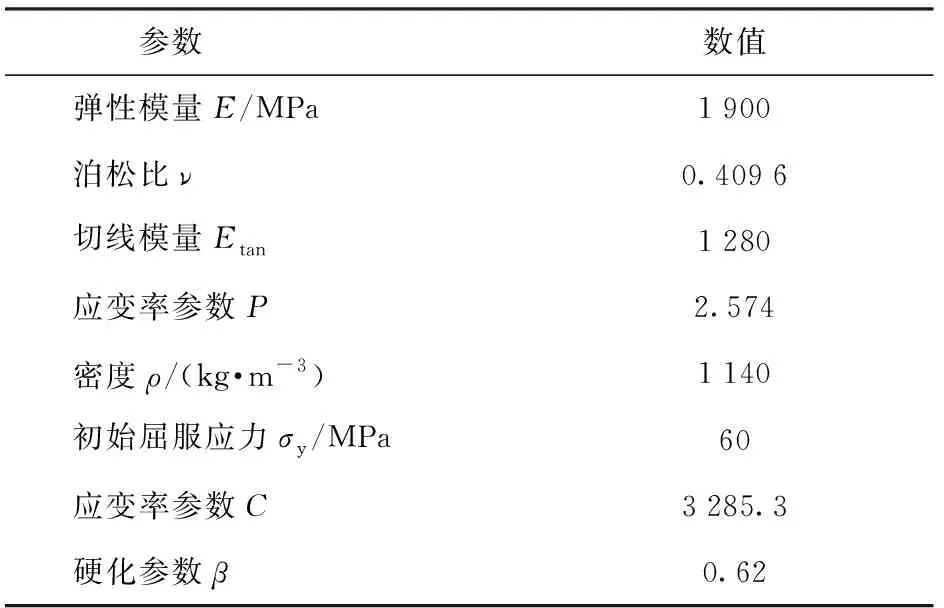
表1 尼龙弹带材料参数Table 1 Material parameters of the nylon cartridge belt

表2 身管和弹体材料参数Table 2 Material parameters of the barrel and projectile body

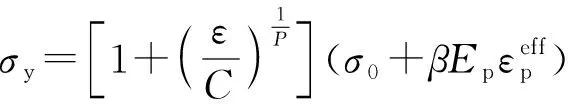
(15)

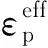
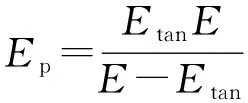
(16)

为切线模量，为弹性模量。

2.4 接触、载荷及边界条件

采用面- 面侵蚀接触定义尼龙弹带与身管之间的接触，尼龙弹带与弹体之间定义为自动接触，从初始时刻即开始生效作用，定义尼龙弹带与身管之间的静摩擦系数与动摩擦系数分别为015和010。同时，对于身管采用全自由度约束，而仅允许弹带和弹体沿身管轴向平动和转动。由于坡膛长度为21 mm，相对全身管很短，埋头式弹丸挤进过程非常短暂，在火药燃烧初期达到最大压力前就已经完成，有关研究指出仅在挤进时期，弹底压力与膛底压力的误差为292，膛底压力与坡膛压力的误差为379，计算挤进时期的材料变形过程时，忽略弹底压力与坡膛压力的误差，因此以某装药条件下实际射击过程中测得的坡膛处压力作为动载荷，加载到埋头式弹丸底部。同时，基于埋头式弹丸发射新原理，在挤进开始之前，弹丸已在可燃导向筒内自由滑动一段距离，因此将试验测得弹丸在起始达到坡膛处的速度=30 m/s作为初速度，也加载到弹体和尼龙弹带上。

2.5 有限元模型验证

为验证23节模型的准确性，首先针对某常规穿甲弹的模拟挤进试验，进行相应的数值计算。文献[20]试验中测量了挤进过程中坡膛处压力及弹丸运动位移随时间变化关系。计算时将所测得的坡膛处压力(见图3)作为弹底压力边界条件。图4为数值计算与模拟挤进试验的弹丸位移对比图。由图4可知二者吻合很好：由于69 ms之前火药燃气提供的弹底压力还不足以克服弹丸挤进阻力，弹丸并未运动，其位移始终为0；69 ms时，弹带开始出现塑性变形，弹底压力大于挤进阻力，弹丸开始沿轴线向前挤进；8 ms时弹丸运动位移开始显著增加，数值仿真和试验得到的弹丸位移最大误差出现在875 ms，此时二者相对误差为776，即在一定范围内所建立的弹丸冲击挤进模型是可靠的。

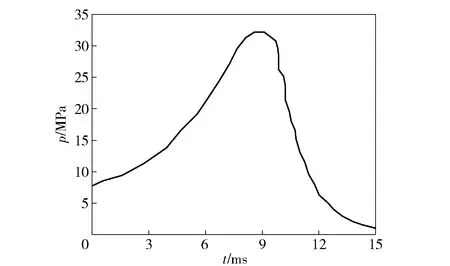
图3 模拟挤进试验测得的坡膛处压力曲线Fig.3 Pressure curve within the freebore in the simulated experiment

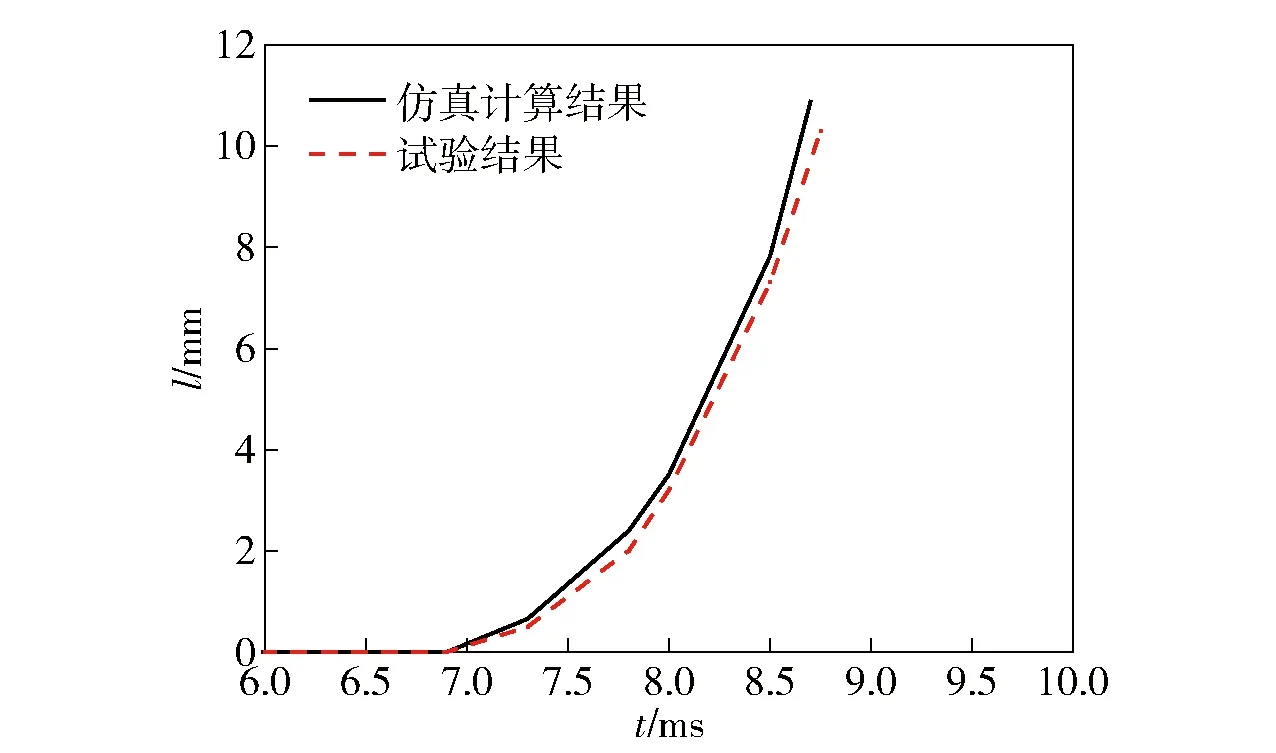
图4 试验与仿真计算结果的弹丸位移对比Fig.4 Comparison of projectile displacement in test and simulation results

3 埋头式弹丸动态冲击挤进结果分析

本节采用已建立的有限元模型针对某40 mm埋头式穿甲弹的动态冲击挤进过程进行数值仿真研究，分析其中的应力应变特性及挤进阻力等变化规律。

3.1 弹带材料形变机制分析

由于埋头式弹药结构的特殊性，在挤进开始时弹丸就具有一定的初速度。图5为一级点火后期弹带变形的应力状态云图。该阶段主装药还未完全燃烧，弹底压力较小。因此，弹丸以一定的初速度做减速挤进运动。

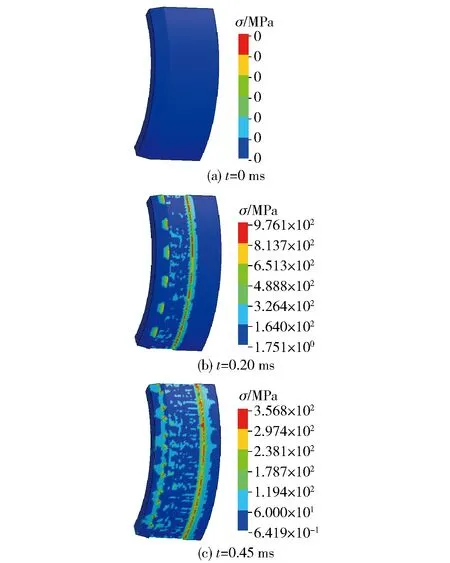
图5 减速阶段弹带变形的应力云图Fig.5 Stress nephogram of belt deformation in the deceleration stage

由图5可见：0 ms为挤进的初始阶段，此时弹带的应力为0 MPa。之后，弹丸在自身原有初速度和一次点火后期燃气推动下，受坡膛挤压开始向前运动；02 ms时，弹丸以一定速度冲击坡膛，首先弹带表面受坡膛挤压使其应力逐渐升高，随着弹丸运动，阳线突出量逐渐明显，在阳线挤压部位其应力值也逐渐上升，并达到初始屈服极限60 MPa；045 ms时，已经进入一级点火最后时期，弹底压力降到了最小值，弹丸速度也接近于0 m/s，弹带后部还未完全进入坡膛，弹带前部与阳线接触的位置已出现微小的刻痕，此时由于弹丸速度的降低，弹带所受应力也逐渐降低。

埋头式弹丸与普通弹丸不同的是存在二级点火阶段，此时主装药开始全面燃烧，弹底压力又逐渐上升，虽然弹丸速度仍近似为0 m/s，但是在主装药燃气的推动下，弹带受坡膛挤压，主要发生弹性形变并伴随有部分塑性形变产生，如图6所示。由图6可见，随着时间的推移，弹带挤入处的应力开始逐渐增大，且由于主装药的燃烧，提供的弹底压力也越来越大，因此其应力上升速率也越来越快。然而，弹带大部分单元应力值还未达到其材料的初始屈服极限60 MPa，因此弹带材料主要还是发生弹性形变，仅表面少部分单元发生了塑性形变。

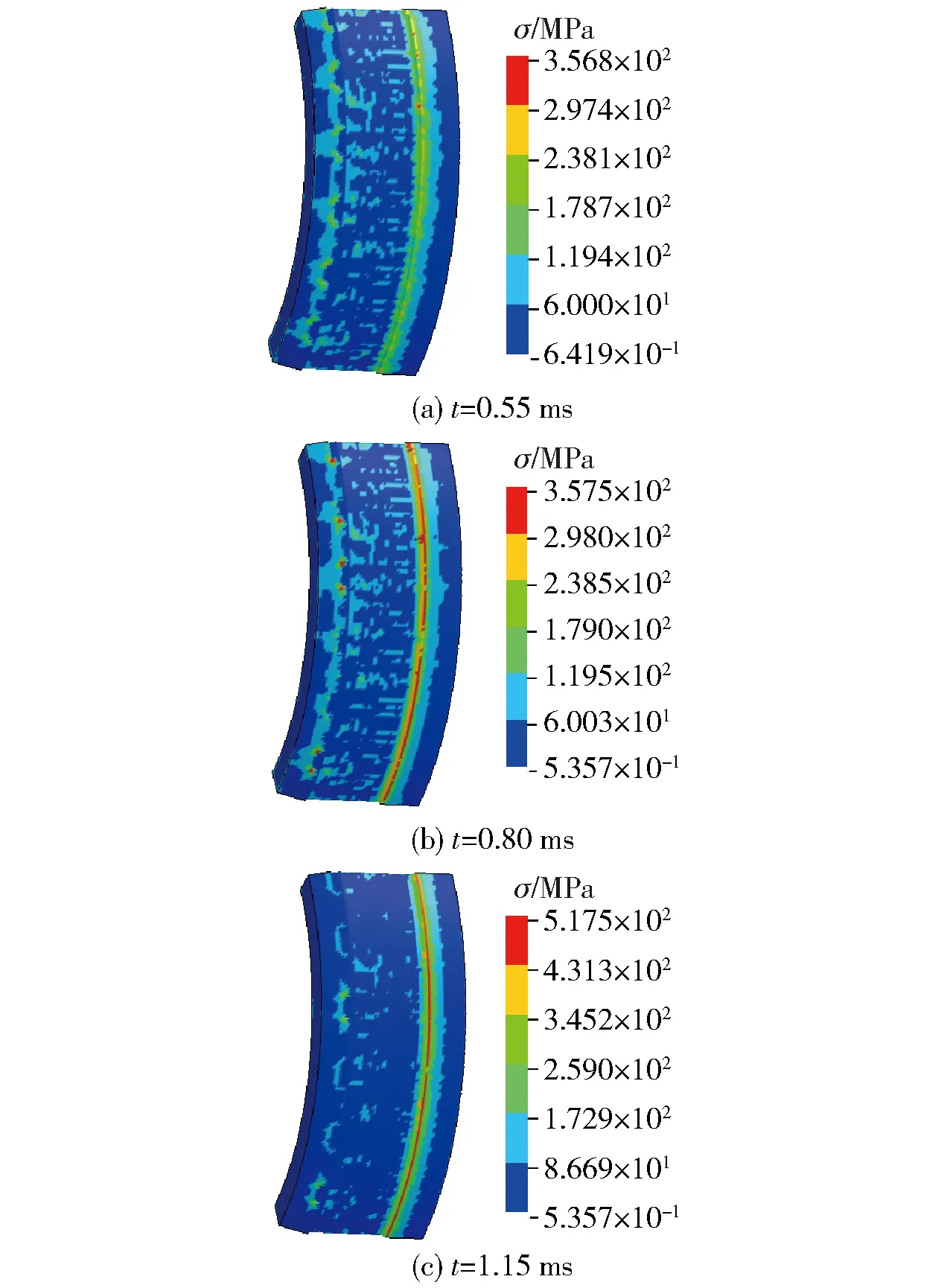
图6 停止阶段弹带变形的应力云图Fig.6 Stress nephogram of belt deformation in the stopping stage

随着二级点火阶段主装药的燃烧，弹底压力进入迅速上升期，弹丸克服阻力开始加速运动，弹带挤压进入坡膛处的应力上升，且达到其材料的屈服极限，开始损伤被删除，如图7所示。由图7可见：16 ms时，整个弹带已经完全进入坡膛，膛线开始刻蚀弹带，弹带与阳线接触部分的应力升高；185 ms时，弹带已经全部挤进身管膛线部，挤进过程结束，且弹带刻痕形成的凹槽达到最深并与膛线紧密贴合，弹带所受应力迅速减小。

图7 加速阶段弹带形成刻槽的应力云图Fig.7 Stress nephogram of groove formation in the belt during acceleration

3.2 弹带材料断裂失效模式分析

为深入探究弹带材料在挤进时期的刻槽形成机理，通过其塑性大变形区域的应力状态来分析材料的断裂失效机制。图8和图9分别为175 ms时弹带材料的内部应力三轴度和内部Lode参数云图，其中应力三轴度代表静水压力-与等效应力的比值，其表达式为

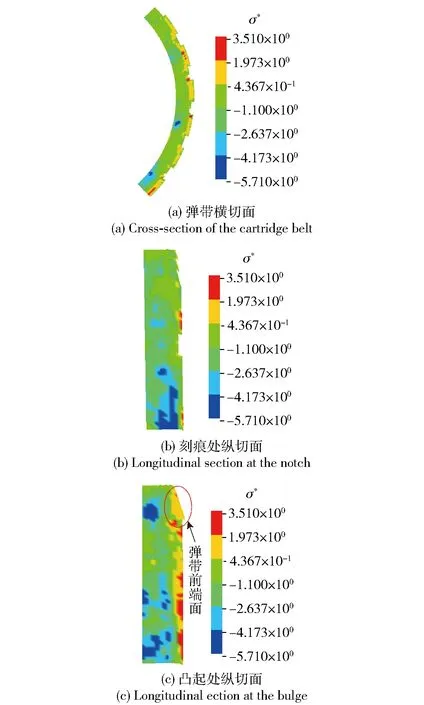
图8 弹带内部应力三轴度云图Fig.8 Triaxiality nephogram of internal stress inside the cartridge belt

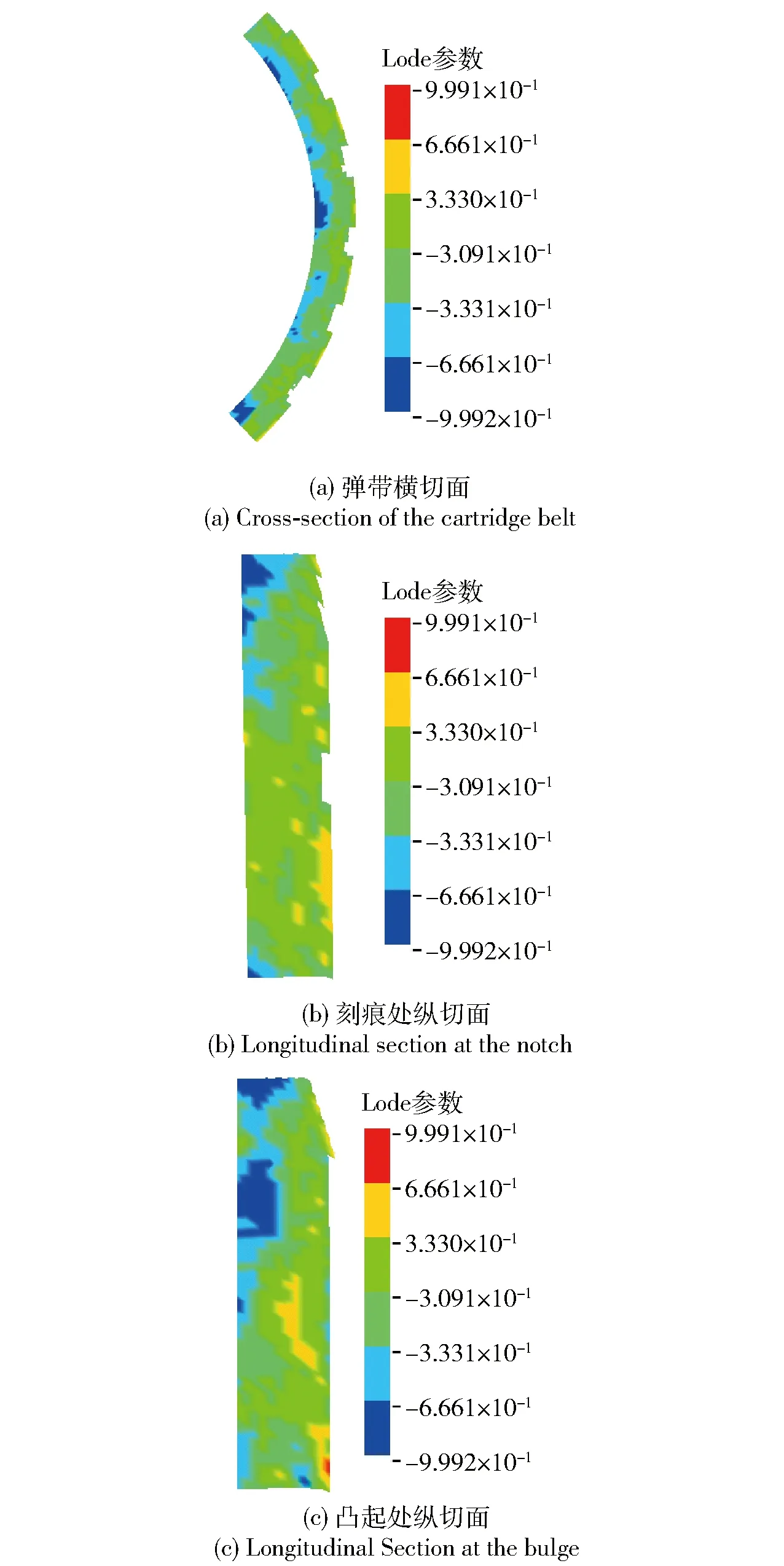
图9 弹带内部Lode参数云图Fig.9 Lode parameter nephogram inside the cartridge belt

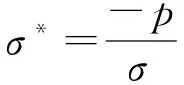
(17)

的值代表了弹带所处的应力状态，而Lode参数为排除球形应力张量对塑性应变的影响，从而反映应力特征的参数。

由图8(a)和图9(a)可知，整个弹带材料直接受身管阳线作用的区域应力三轴度小于0，而其Lode参数也均小于或者接近0。这就意味着在弹带材料的挤进过程中，该区域发生断裂失效模式主要是以剪切失效为主。从图8(c)中可知，弹带前端面的应力三轴度大于0，即由于坡膛摩擦阻力的作用，弹带前端面在运动过程中受到了与膛线切向方向相反的拉伸作用。从图8(b)中可见，弹带内部应力三轴度大多处于小于0的状态，Lode参数基本都小于或接近0，由此可判断出，弹带内部主要还是处于压剪状态。

3.3 弹带内部应力及应变特性

图10和图11分别为挤进不同时期弹带表面的等效应力曲线图和等效塑性应变曲线图，图中各点的具体位置如图12所示，其中点、点和点分别位于弹带与身管阳线对应的位置，点、点和点分别位于弹带与身管阴线对应的位置。由图10可见：由于、两点位于弹带表面，在挤进初始时期该处应力就迅速上升，至材料失效硬化而被剪切后，导致其应力又迅速下降至0 MPa；当、位置处的材料失效后，弹带内部、、、四点处的应力值随着弹丸速度和弹带挤进量的减小也均逐渐减小；当弹丸处于停止阶段时，四点的应力值也均基本保持不变；最终，、两点处的材料被身管阳线剪切失效并形成刻槽，其应力快速下降至0 MPa；与身管阴线接触的、位置处的材料单元并未失效被剪切，因此在挤进完成后其应力也不为0 MPa，且整个挤进过程中其应力波动也较小。由图11可知：在挤进初期，弹带表面、点就达到材料失效条件被删除；弹带内部、、、四点在挤进初期即弹丸减速阶段，其等效塑性应变值均不断上升，随着弹丸速度下降至0 m/s，其等效塑性应变值均保持不变；当身管膛线再次开始刻蚀弹带，并最终刻蚀至、两点所在位置时，该两点处的材料迅速失效，等效塑性应变值下降至零，而、两点处的弹带内部等效塑性应变值在后期始终保持不变。

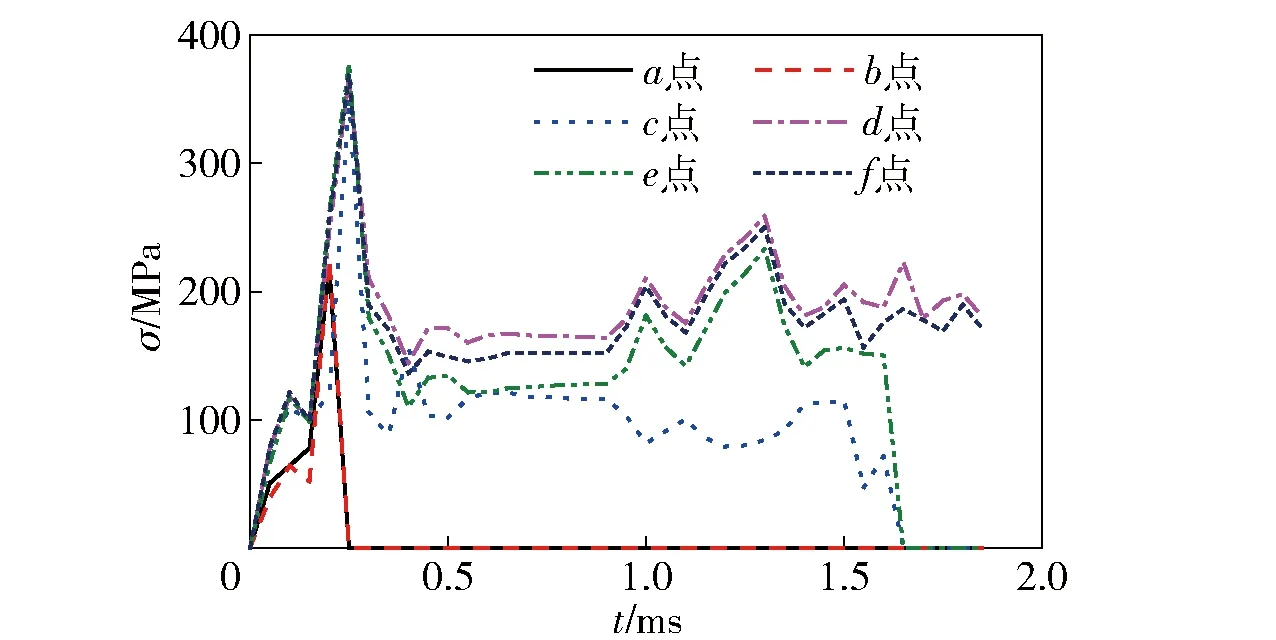
图10 各特征点等效应力曲线Fig.10 Equivalent stress curve for each feature point

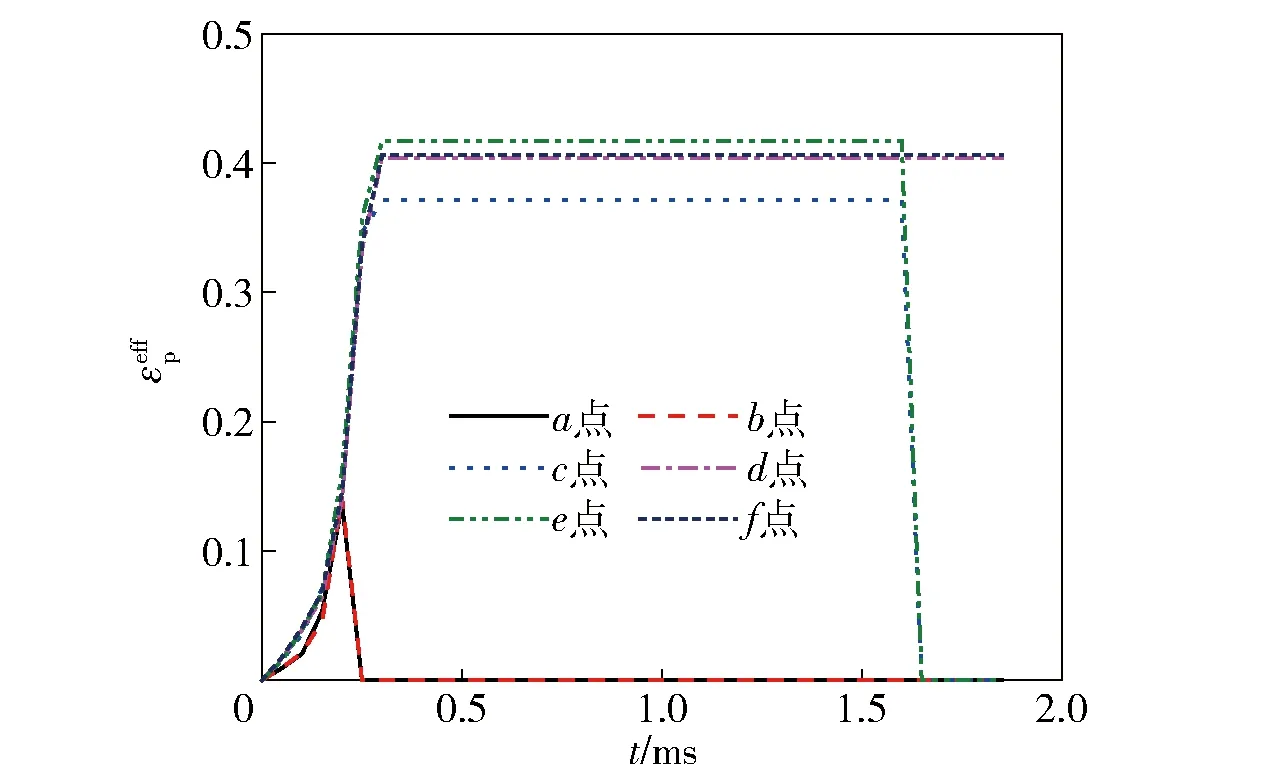
图11 各特征点等效塑性应变曲线Fig.11 Equivalent plastic strain curve for each feature point

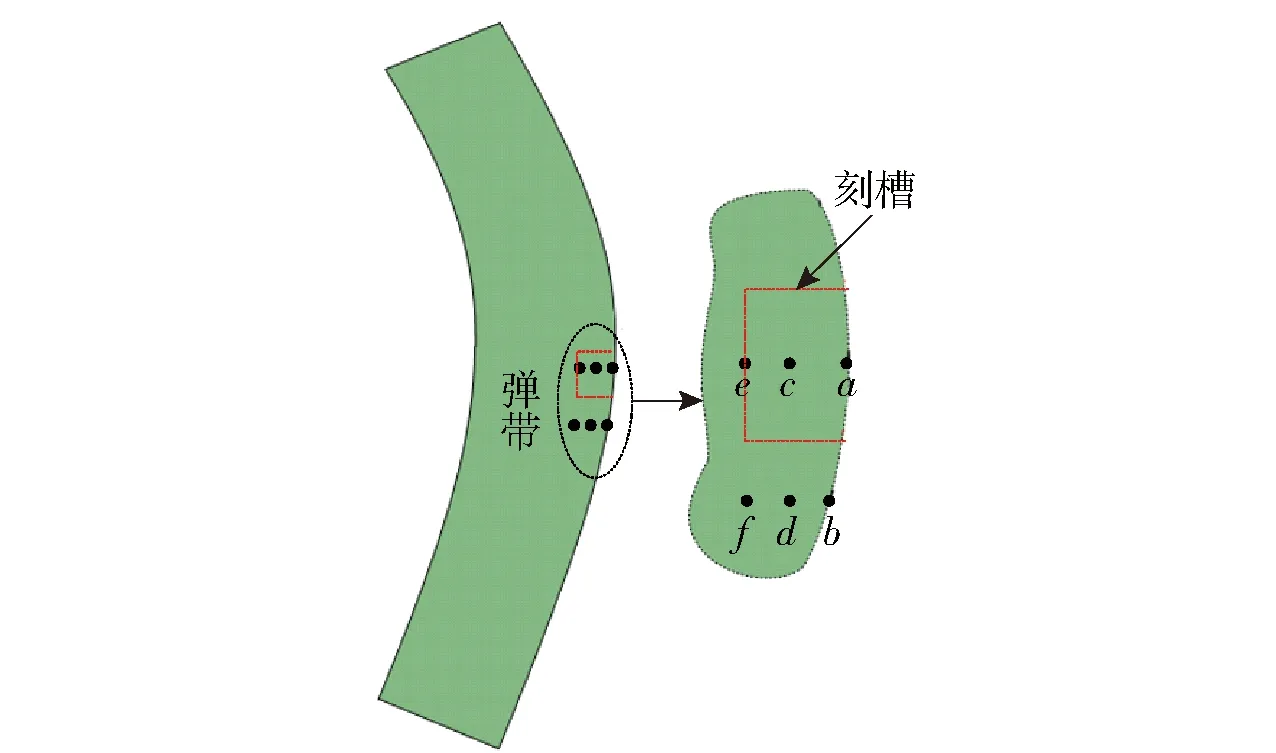
图12 弹带各特征点位置示意图Fig.12 Schematic diagram of feature points on the cartridge belt

3.4 弹丸挤进阻力特性及拟合公式

图13为模拟得到的弹丸挤进阻力与位移随时间变化曲线。由图13可知：初始时刻弹丸就具有较大的速度，弹带需要发生大的变形才能挤入坡膛；因此弹带所受到挤进阻力较大；随着挤进过程的进行，弹底压力还很小，弹丸冲击挤入坡膛的速度不断降低，其挤进阻力也随之降低；随着二级主装药的燃烧，弹底压力开始迅速上升，弹丸不断冲击坡膛，弹带表面材料发生塑性硬化，且塑性变形量增大并损失失效，挤进阻力也迅速增加，而弹丸在弹底压力的作用下也逐渐开始克服阻力继续挤入坡膛。135 ms时，挤进阻力达到最大值30 000 N；随着时间的继续推移，弹带逐渐挤入身管全深膛线，其变形量开始减小，挤进阻力也随之减小；185 ms时，弹带完全挤入身管全深膛线，挤进过程结束，变形产生的阻力下降至0 N，挤进运动阻力仅由摩擦阻力构成。

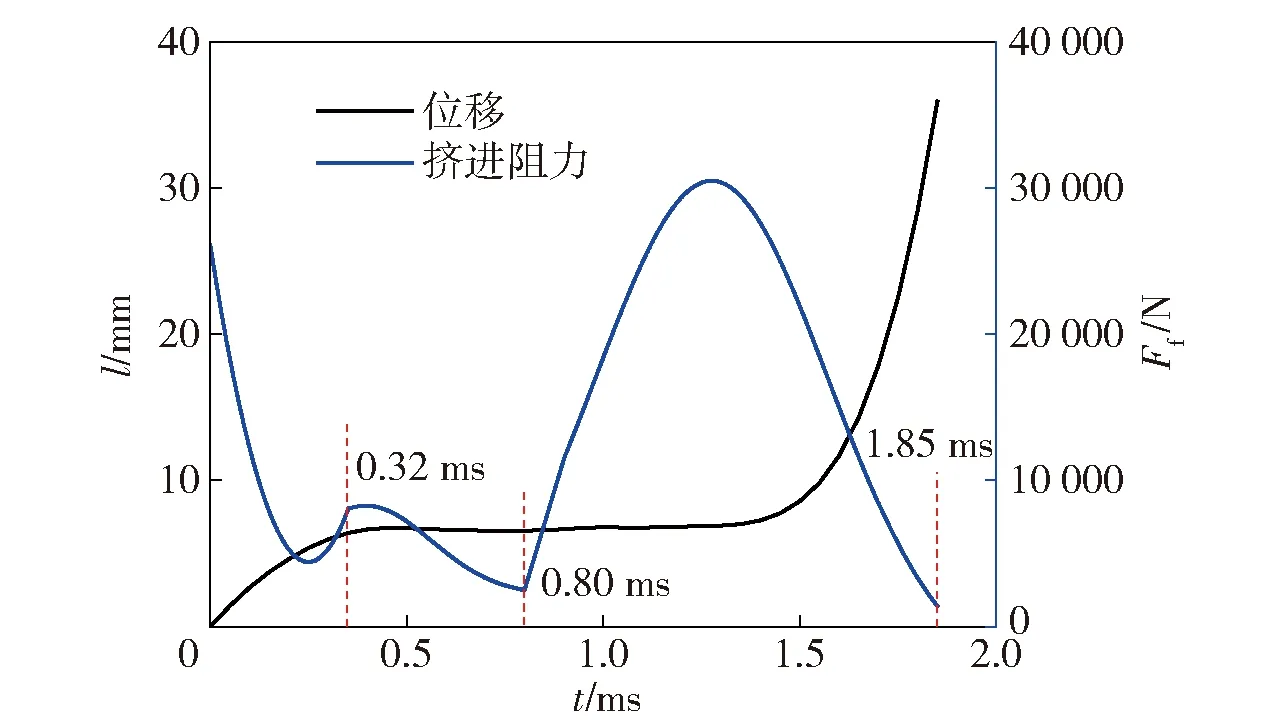
图13 弹丸挤进阻力与位移曲线Fig.13 Curve of extrusion resistance and projectile displacement

当弹带刚好全部进入坡膛时，通过其挤进阻力与位移关系可积分计算出弹带挤进阻力做功耗能为173 J，而通过弹底压力与位移关系，同理可积分计算出该过程中火药燃气提供给弹丸运动的总能量为503 J，即弹带挤进耗能占火药燃气提供给弹丸总能量的34。当弹带完全挤入身管全深膛线时，采用同样计算方法可得到弹带挤进阻力做功耗能为266 J，火药燃气提供给弹丸运动的总能量为3 761 J，此时挤进阻力耗能占比为6，即挤进过程消耗的能量较大，在内弹道性能计算中不可忽略。

采用高斯公式对图13中的弹丸挤进阻力曲线进行分阶段拟合如下：

(18)

式中：为时间(ms)。将拟合得到的挤进阻力公式代入上述两级点传火的内弹道方程中，即可建立计及动态冲击挤进过程的内弹道一体化精确模型。

4 内弹道一体化模型验证与分析

4.1 内弹道一体化模型的验证试验

为验证本文所建立的内弹道一体化模型的正确性，针对某40 mm埋头式穿甲弹进行靶场射击试验，以获得真实射击条件下的内弹道特性。采用瞬态压力传感器、电荷放大器以及数据采集设备等构成内弹道压力测试系统，对弹丸运动过程中的膛压进行实时测量，并采用靶板测速装置获得弹丸初速。图14为试验数据处理流程图。

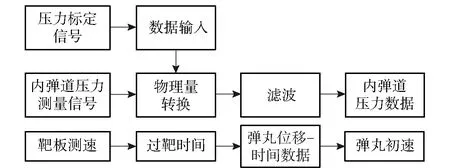
图14 试验数据处理流程Fig.14 Flow chart for experimental data processing

4.2 内弹道仿真与试验结果对比分析

采用本文所建立内弹道一体化精确模型，对某40 mm埋头式穿甲弹的整个内弹道过程进行数值计算，并与实际射击条件下的测试结果进行对比。图15为内弹道一体化精确模型数值计算、经典内弹道数值计算与试验测得的膛内压力对比曲线图。由图15可知：内弹道一体化精确模型的数值计算结果与试验得到的压力曲线在整个时间范围内均吻合较好，试验测得的最大膛压为5083 MPa，弹丸炮口初速为1 5134 m/s；采用内弹道一体化模型计算得到的最大膛压为5179 MPa，弹丸炮口初速为1 5037 m/s，其相对误差均小于2；经典内弹道仿真计算得到的最大膛压为4523 MPa，炮口初速为1 3483 m/s，其相对误差均大于10；由于经典内弹道模型忽略了埋头式弹丸挤进的动态过程，在185 ms(挤进完成时刻)之前，采用经典内弹道模型计算得到的压力平均值明显大于试验值，这种差距随着弹丸的运动，越来越明显。由于本文所建立的内弹道一体化模型将二次点火的内弹道运动和能量方程分成挤进时期模型和挤进结束后模型两个阶段，在弹丸挤进结束时能提供更为准确的数据作为弹丸在全深膛线中运动的开始。当弹丸在全深膛线中运动时挤进结束，挤进阻力也无需再考虑，因此一体化模型计算得到的压力曲线与试验测试结果在该阶段也吻合较好，即所建立的计及埋头式弹丸冲击挤进过程的内弹道一体化模型能够更加精确地预测其内弹道特性。

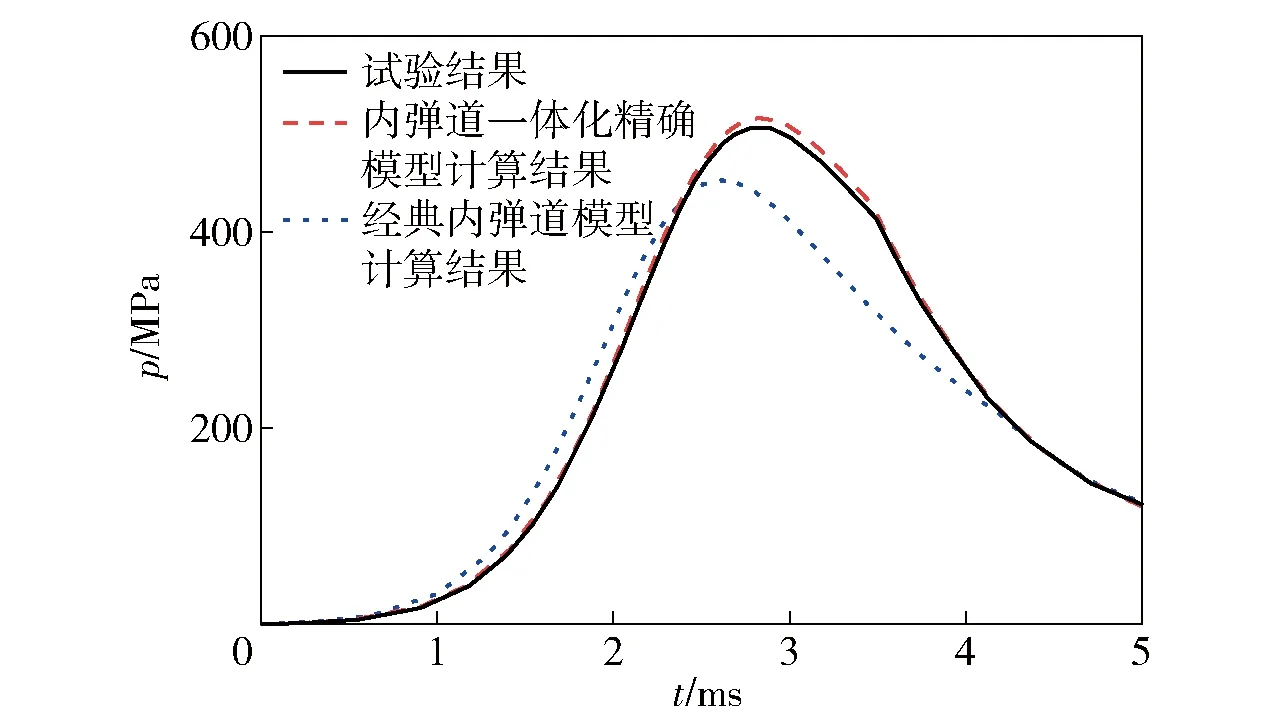
图15 膛内压力数值计算结果与试验结果对比Fig.15 Comparison of average breech pressure in numerical calculation and test results

5 结论

本文采用显式动力有限元法建立了某埋头式穿甲弹动态冲击挤进坡膛的三维有限元模型，基于双线性随动塑性材料模型进行了某40 mm埋头式穿甲弹冲击挤进动力学数值仿真。在此基础上，构建了埋头式穿甲弹挤进过程初始内弹道与挤进完成后内弹道的一体化精确模型，并进行了数值计算。得到以下主要结论：

1)埋头式弹丸初始以一定速度冲击挤入坡膛，弹带材料经历了弹性变形到塑性变形，且产生了塑性硬化和局部大变形，整个弹带材料直接受身管膛线作用的区域发生断裂失效模式主要是以剪切失效为主，弹带内部主要处于压剪状态。弹带与身管阴线、阳线接触部位均只有表面区域发生较大的塑性变形，内部区域的塑性变形量都比较小。

2)埋头式弹丸初始挤入坡膛时所受到的挤进阻力较大。随着挤进过程的进行，弹丸冲击挤入坡膛的速度不断降低，其挤进阻力也随之降低。在主装药燃气作用下，弹底压力又迅速上升，弹丸不断冲击坡膛，弹带表面材料发生塑性硬化，并损失失效，挤进阻力也迅速增加；随着弹带逐渐挤入身管全深膛线，其变形量减小，挤进阻力也逐渐减小。最终，挤进过程结束，挤进阻力下降至0 N。

3)采用高斯公式对弹丸挤进阻力曲线进行拟合，并将其与埋头式弹丸内弹道模型进行一体化建模，通过数值模型得到了膛内平均压力随时间变化曲线，并与试验结果进行了对比，验证了该模型的准确性，可为后续埋头式弹药内弹道设计提供参考。