锥直型喷嘴内近壁处流动特性的大涡模拟

姜天文，黄中伟，李敬彬

中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

0 引言

水射流技术是指利用高压泵产生高压水进行作业的技术，该技术通过喷嘴将压力转变为高度聚集的水射流，能够完清洗、切割、破碎等工艺，广泛应用于石油行业，具有无污染、成本低等显著优势[1-3]。随着科技的发展喷嘴亦被应用到其他方面，例如获得满足光学加工要求的等离子体射流[4]和冲击式速冻机[5]以及3D打印技术[6]等方面。喷嘴作为射流的终端执行机构，影响着射流特性和设备工作效率，需进行单独研究。在多种喷嘴中锥直型喷嘴因其具有良好的集束能力和较为稳定的工作特性而广泛被使用。

锥直型喷嘴结构由收缩段、直管段、扩孔段组成，因工作目的不同而有所差异。收缩段用于集束流体、聚能；直管段则用于稳定流动特性；扩孔段则用于控制射流出口扩散角以及控制空化等。在石油行业应用中锥直型喷嘴一般不考虑扩孔段，本文主要针对喷嘴内部近壁处流动特性研究，相关研究不考虑扩孔段。前人对喷嘴结构已做了相关研究。

沈华建[7]、Zhaolong Ge[8]等人针对高压水射流煤层割缝增产射流喷嘴进行了数值模拟研究，对喷嘴收缩段收缩角、直管段长度进行了敏感性分析，并给出了建议性的喷嘴结构，通过实验对喷嘴优化前后切割能力进行验证。刘文杰[9]通过数值模拟发现喷嘴锥角对射流参数影响较大，射流速度随锥角增大先增大后减小。H.Vahedi Tafreshi[10]、马文涛[11]则通过实验和数值模拟对锥直型喷嘴和锥型喷嘴流场特性和破岩特性进行了对比分析，以射流等速核长度为目标，模拟结果表明锥直型喷嘴优于锥型喷嘴和平直型喷嘴。陈廷兵[12]则对不同喷嘴破水合物效果进行对比分析，通过数值模拟和正交实验对优选结果进行对比，给出了锥直型喷嘴的优化结构参数。施红辉[13]则采用模型模拟了不同喷嘴结构的氮气射流，模拟结果表明锥直型喷嘴具有更好的集束性与扩散性，而平直管喷嘴具有最大的有效作用距离。此外在采用水射流消除残余应力时，得益于其直管段部分具有稳定射流特性的功能[14]，锥直型喷嘴具有更好的应用效果。何枫[15]则对喷嘴内流道型线对射流的影响进行了模拟，结果表明内部型线主要影响喷嘴出口附近的速度和压力分布，同时指出维多辛斯基曲线可以获得更好的射流特性。程新颖[16]亦对圆弧形型线结构喷嘴进行了模拟及实验，得出圆弧形喷嘴射流密集性及压降损失均小于常规锥直型喷嘴。

学者们大多从锥直型喷嘴轮廓方面对喷嘴结构进行优化，分析喷嘴内部型线轮廓对射流特性的影响，并给出特定应用环境的最优参数，但针对喷嘴内部流动特性相关研究较少，而喷嘴内部流动状态影响着外部流场特性，因此研究喷嘴内部流动状态对喷嘴结构优化有进一步的指导作用。

本文采用大涡模拟(Large Eddy Simulation, 简称LES)模型对喷嘴内部流动状态进行了模拟，对近壁处流动特性进行模拟，分析近壁处边界层转捩及分离位置，进而研究边界层转捩及分离对外部流场特性的影响，对锥直型喷嘴进一步优化具有参考意义。

1 计算模型及计算方法

1.1 计算模型

本文研究锥直型喷嘴结构如图1所示。锥直型喷嘴结构主要分为收缩段和直管段，收缩段主要用于聚集流束，使流体加速；直管段用于稳定流动状态，降低流体流出喷嘴的扩散角。

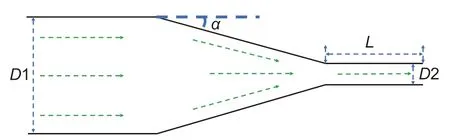
图1 喷嘴结构示意图Fig.1 Nozzle structure

本文锥直型喷嘴的物料尺寸为：入口段直径D1为15 mm，收缩角度为15°，直管段长度L1为15 mm，直管段直径D2为4 mm。X轴为喷嘴中心轴，方向为流体流动方向，Y方向为喷嘴径向方向。

1.2 网格划分

对近壁处边界稳定流动状态进行模拟时，网格要求较高，近壁处边界稳定流动分为黏性底层、过渡层和对数率层，常用无因次壁面距离y+来判断流动的状态，y+＜5时为黏性底层，5＜y+＜30时为过渡层，当y+＞30时为对数率层，为探究整个边界层处流动状态，网格划分采用第一层网格尺寸为y+=1处的真实距离记为。沿壁面y+分布如图2所示。

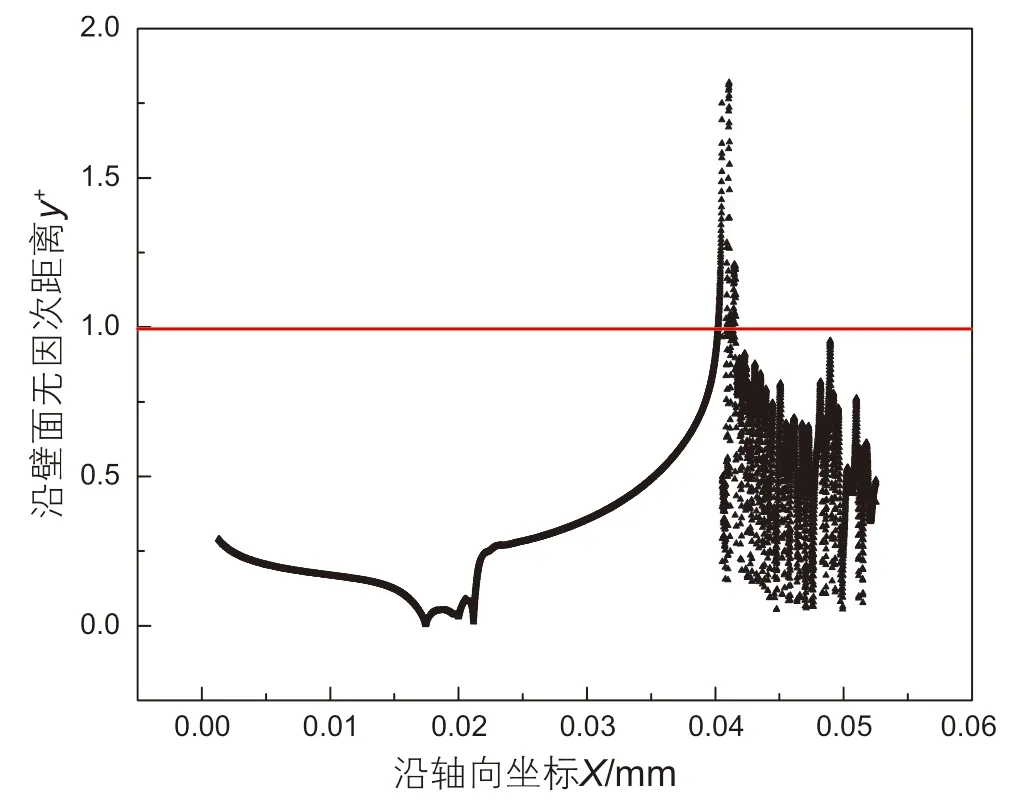
图2 y+沿壁面分布Fig.2 y+ distribution along the muzzle wall

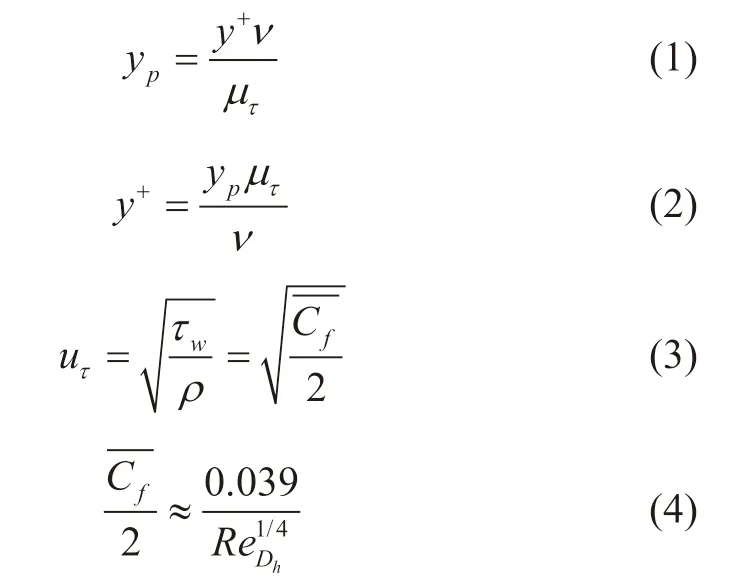
式中为管道摩阻系数经验参数，为管道直径Dh的雷诺数，μτ为剪切速度，m/s，v为动力黏度，Pa·s。

采用结构化网格进行划分，进行第一层网格尺寸计算，边界层为20层，增长速度为1.15，网格如图3所示。在近壁处网格确定以后，为降低计算量进一步优化非近壁处网格，对计算域进行对称处理，同时将中间网格最大面尺寸定为0.001 m，网格数量由86万降低为36万，网格偏斜度最大为0.76，网格质量优。

图3 网格划分Fig.3 Grid

1.3 数值方法

为充分分辨壁面附近的湍流结构，法相采用非均匀网格加密，并通过计算使得第一个节点y+＜=1，采用周期性边界条件，初始平均速度设置为10 m/s，壁面条件为无滑移固壁边界条件。

喷嘴内部流动为湍流，存在大量的弯曲流动和涡流，在进行计算时，考虑到近壁处网格足够精细，壁面函数采用增强型壁面处理(Enhanced Wall Treatment)，采用RNG k-Epsilon 湍流模型进行定常计算到收敛。LES计算的初始流场为刚得到的瞬态速度场。余建阳[17]等人比较了4种不同亚格子模型的计算原理和仿真特性，发现WALE和 KET模型仿真结果更准确，故选择WALE亚格子模型进行非稳态求解。空间离散格式采用有限差分格式，压力—速度耦合基于SIMPLE算法，入口条件为速度入口边界，平均速度设置为10 m/s，出口条件为压力出口边界。时间步长为10-7s。

2 数值验证

为验证数值模型的准确性，在与J.G.M.EGGELS[18]相同的计算参数下进行数值模拟，采用相同的几何模型(管径为95.4 mm)和入口条件(雷诺数为5300)，将本文模拟结果与其实验数据和直接模拟结果进行对比。如图4所示，三者显示出较好的一致性，最大误差为0.03，证明本文模型的准确性。

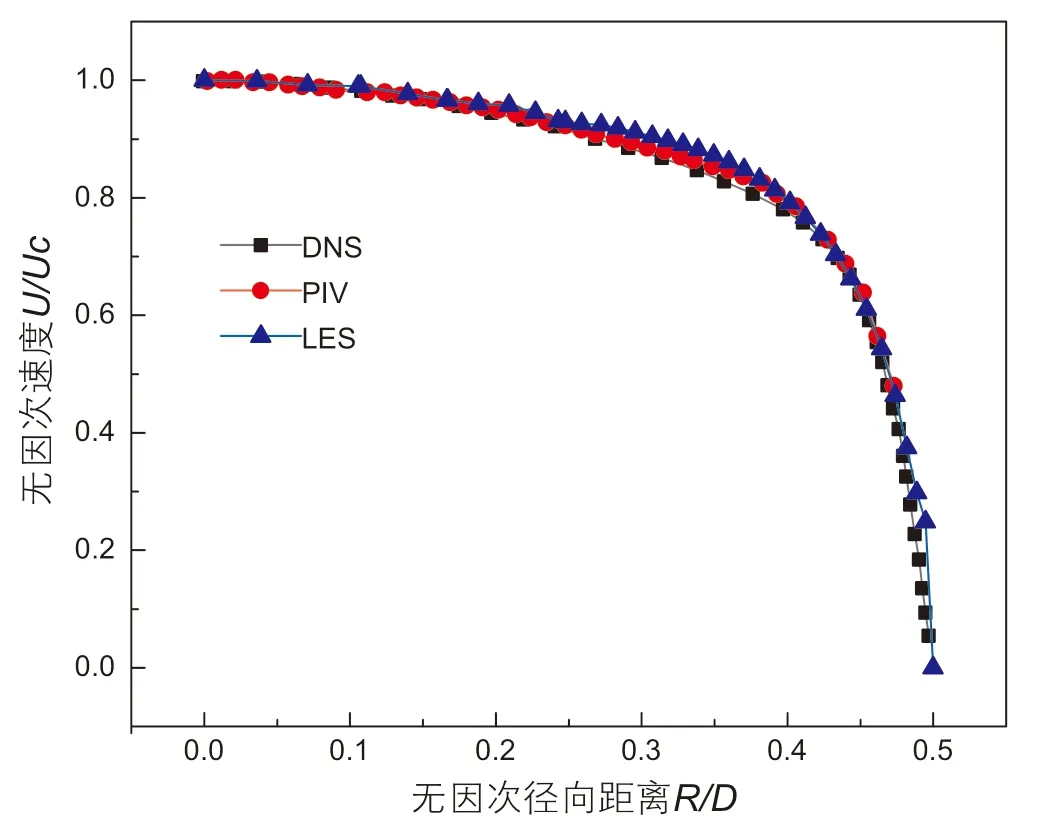
图4 大涡模拟、直接数值模拟、实验数据对比Fig.4 Comparison among LES, DNS and experimental data

3 模拟结果与分析

3.1 喷嘴内速度分布

对喷嘴内整个流场进行分析，发现大涡模拟在网格足够精细的情况下能够准确地模拟喷嘴内部的流动情况及涡的产生情况。如图5所示，喷嘴内主流场速度等值线由入口段均匀分布逐步发展为抛物线形状，进入收缩段后抛物线逐渐变成一条近直线(不考虑贴壁流)，在喷嘴直管段发展成M型。

图5 喷嘴内流线形态及近壁处涡分布Fig.5 Streamline shape in the nozzle and vortex distribution near the wall

在流体开始进入收缩段时，由于来流受到收缩段斜面的激荡，在转折处形成低速区，以涡的形式存在。由于受到斜面影响，边界层在到达转折处前发生了转捩，由原来的层流转变为湍流。此后边界层再次附着壁面稳定形成稳定流，直至直管段入口，在入口处来流与壁面形成15°夹角，来流速度方向保持不变，在直管段入口处形成逆压梯度，发生边界层分离，并开始沿直管段壁面周期性产生有序涡结构。在云图上表现为涡流—稳定流—涡流的周期性出现。如图6、7所示。

图6 直管段内近壁处涡流—稳定流交替出现Fig.6 The vortex-laminar fl ow alternately appears near the wall in the straight pipe

为更好的分析喷嘴内速度分布情况，分别对喷嘴入口发展段、收缩段、直管段以及转折点进行速度分析，各处位置如图8所示。主要喷嘴入口处(X=0.01 m)、收缩起始处(X=0.02 m)、收缩处(X=0.038 m)、转折点(X=0.04053 m)、直管处(X=0.045 m) 5个位置

图8 监测点位置示意图Fig.8 Location of monitoring points

对速度和到壁面距离采用无因次化处理，考虑近壁面处速度分布时仅考虑喷嘴直径的一半，以y+作为无因次距离，。直管处、收缩处、转折点和入口处4个位置的速度分布如图9所示，速度从壁面处迅速增长到主流场速度，如图所示，在转折点近壁面处出现明显的速度峰值，而在直管处则为平滑过渡。

图9 不同监测位置速度分布Fig.9 Velocity distribution

对收缩段入口处进行单独分析如图10所示，在近壁处出现较大的速度波动，判断在该处附近形成涡流，边界层表现为湍流状态，证明边界层在该处附近发生了转捩，与速度云图处发生的涡旋运动状态相互佐证。

图7 直管段近壁处Q等值面Fig.7 Equivalent surface of Q near the throat section wall

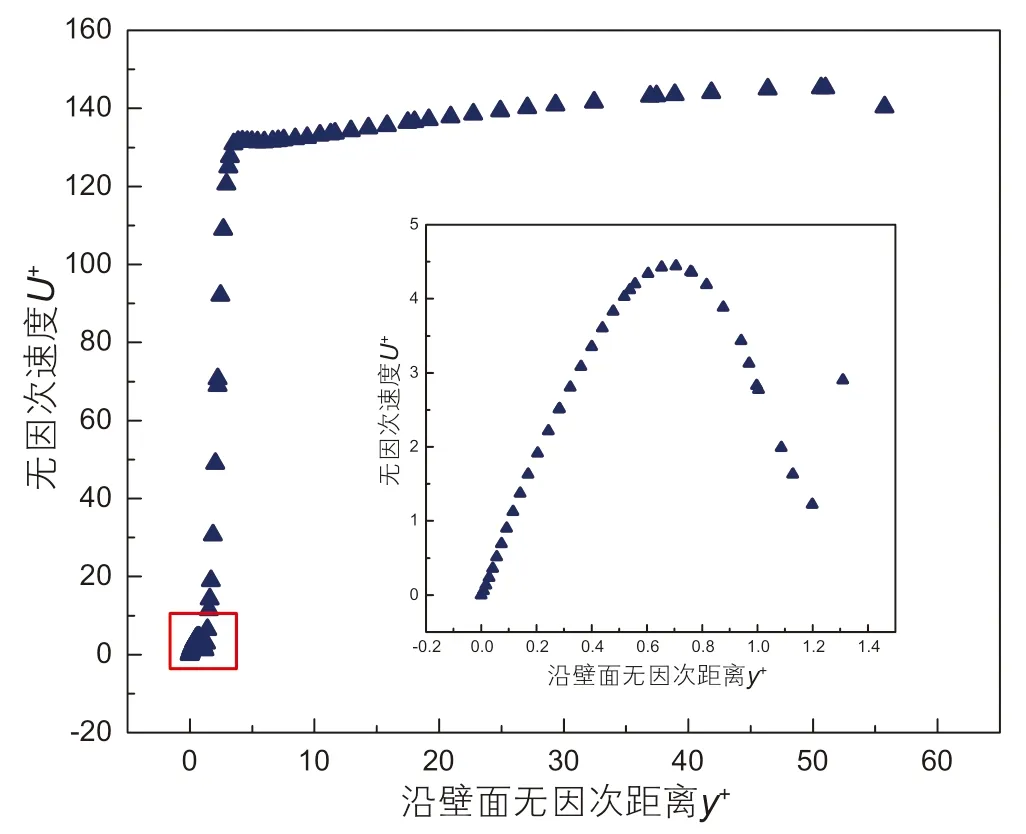
图10 收缩段入口处速度分布Fig.10 Velocity distribution at Converge inlet point

3.2 脉动速度

湍流度表征流动的稳定情况，通常用脉动速度均方根与时均速度之比表示，喷嘴入口处(X=0.01 m)、收缩起始处(X=0.02 m)、收缩处(X=0.038 m)、转折点(X=0.04053 m)、直管处(X=0.045 m) 5个位置的脉动速度情况如图11所示，从图中可以看出，在直管处和收缩段入口处湍流度最大，分别达到了24%和22%，而转折点、入口处和收缩处的湍流度均在10%以内。转折点属于临界点，在该点附近为边界层分离、转捩的临界位置，此时保持转捩前的流动状态。

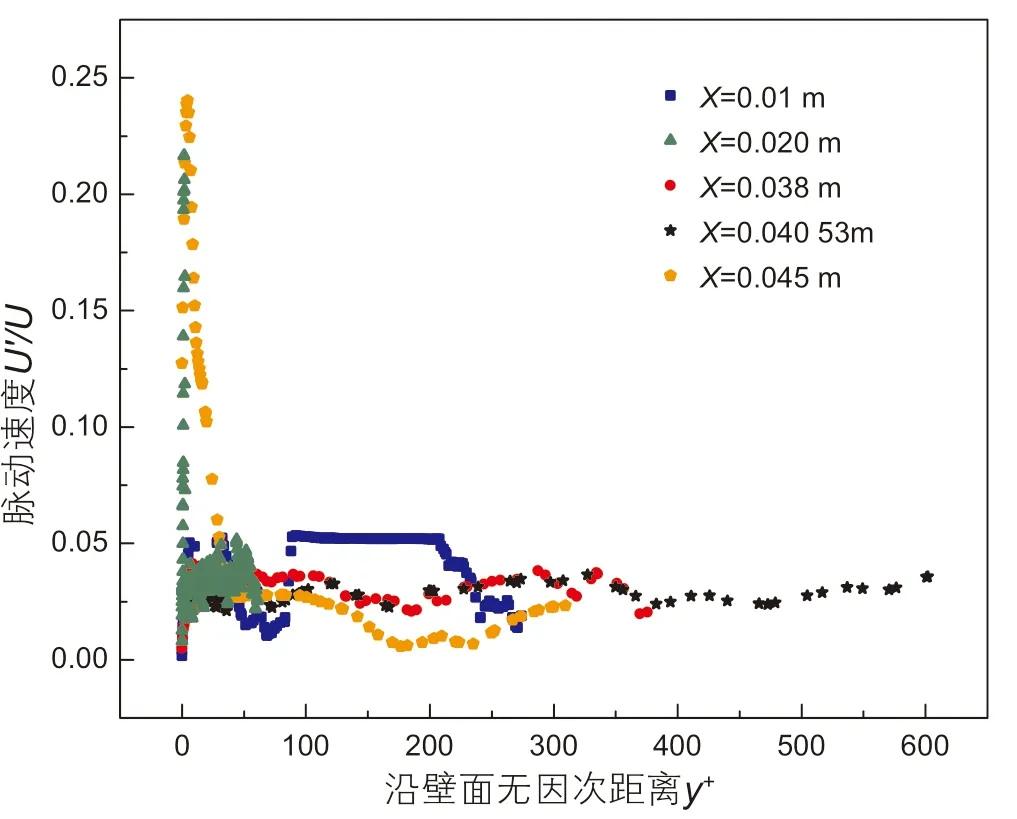
图11 不同位置脉动速度分布Fig.11 Pulsating velocity distribution

整个过程为带有10%湍流度的流体在入口段处流动逐渐稳定；伴随着湍流度的降低，流体到达收缩段时受到收缩斜面的激荡而发生边界层转捩，边界层由稳定流转变为湍流，湍流度急剧升高，在收缩段中均匀缩径，流动逐步趋于稳定，湍流度逐步稳定；当流体经过收缩段进入直管段后由于边界层发生分离与转捩，并周期性的出现有序涡结构，整体流动不稳定，湍流程度高，湍流度增大。

3.3 壁面压力

图12 喷嘴上壁面瞬时动压分布Fig.12 Instantaneous dynamic pressure distribution

从图中可以看出在入口段处壁面动压较低，此后经过收缩段时动压逐渐增大，在收缩段出口处和直管段入口处显示最大动压值，并在该处附近急剧增加而后降低，随后在直管段处于一种周期性增长与降低。

壁面动压较低时表明近壁处流体运动更为稳定，动压值越大，流动速度越大，雷诺数越大，近壁处流动越不稳定。据此可进行如下分析，收缩段起始处近壁处流动受到激励后形成涡结构，但该涡结构能量较弱而消弭，不能够继续发展，且该处流动速度整体较低，因此动压值较低；进入收缩段后受到收缩斜面的激荡，流体逐渐被加速，动压逐渐增加。在刚进入收缩段时未观察到动压值明显增加，这是由于来流速度较低承受激荡能力较强，且总体压力较低；在收缩段出口和直管段入口位置，此时速度已达到峰值，且由于刚运动至喷嘴直管段入口处位置，上下流体具有不同方向的速度相互冲撞，达到了完全湍流状态，流体完全处于无规则大范围运动，边界层厚度被压缩至最薄，近壁处流动速度达到最大值，在该处附近表现为动压急剧升高至峰值后急剧降低。到达直管段后受限于直管段直径，湍流程度受到限制并逐渐趋于稳定，由于边界层在此处附近发生了分离，且在直管段内会出现涡结构的有序出现，这与动压呈现循环增加-降低-再增加的现象一致。

3.4 速度梯度

为深入了解喷嘴内部流动特性，对入口处、收缩段起始处、直管处、收缩处、和转折点五个位置进行速度梯度分析。图13(a)显示了dUx/dy沿Y轴的分布，转折点近壁处速度梯度最大，直管处和收缩处次之，收缩段起始处位置速度梯度最小。速度梯度在主流场区域基本为零，较大的速度梯度仅出现在喷嘴近壁处，鉴于本文模拟的速度较高，边界层厚度较小，呈现出速度梯度急剧升高的现象。图13(b)显示了dUy/dx沿Y轴的分布，大致趋势与图13(a)相似，转折点速度梯度最大，入口处速度梯度(图中局部图)最小，但在形式上略有差别。入口处速度梯度成正弦曲线形式，分析原因可能为Y方向速度分量受湍流度影响较大，在入口段处Y方向速度分量较低，直管处速度梯度未呈现对称分布，分析与初始条件有关。

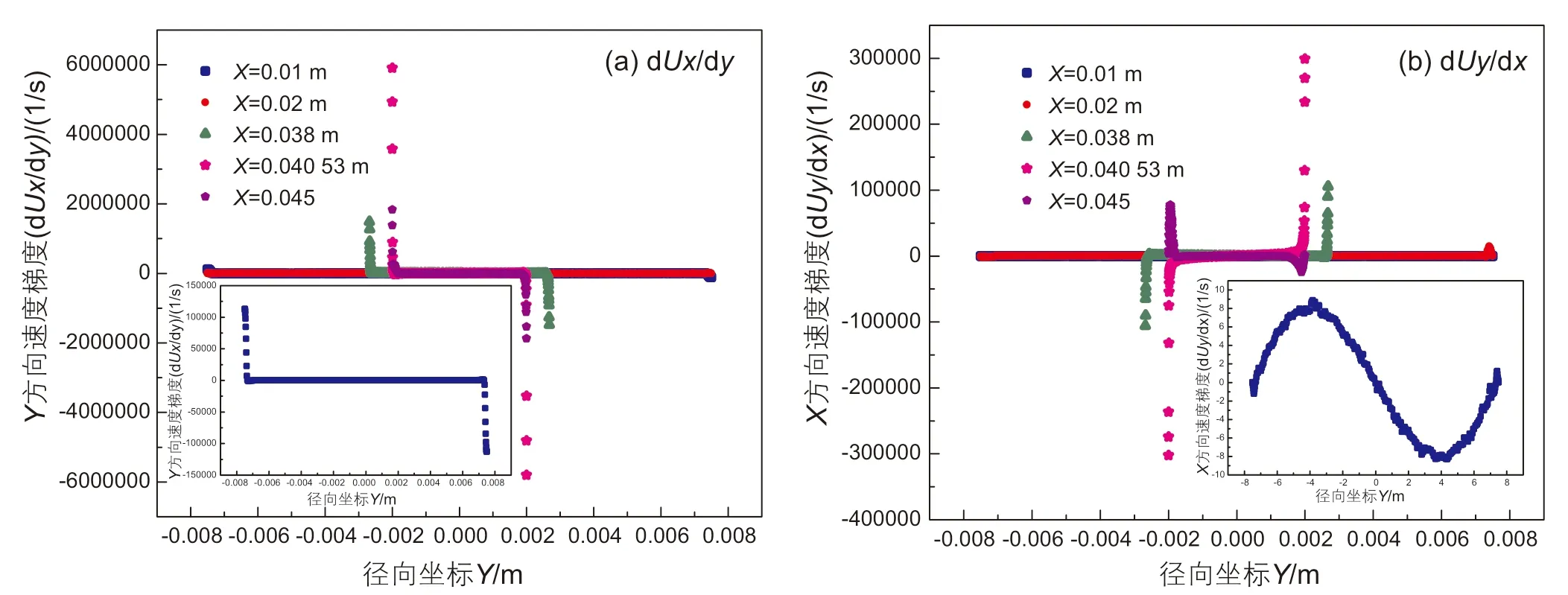
图13 不同位置沿X方向剪切速度分布Fig.13 Velocity gradient distribution at different positions

通过沿喷嘴截面速度梯度分布可以看出，速度剪切主要发生在喷嘴内近壁处，如图14(a)所示。Y速度分量速度梯度主要分布于0＜y+＜50位置，而X速度分量速度梯度主要分布在0＜y+＜20处。

图14 不同位置沿y+剪切速度分布Fig.14 Distribution of velocity gradient at different positions

3.5 壁面剪切力

壁面剪切力与沿壁面垂直方向速度梯度相关，一定程度上表征摩擦阻力的大小。对喷嘴上壁面剪切速度进行监测，平均壁面剪切力结果如图15(a)所示。忽略入口速度条件的影响，壁面剪切力在收缩段入口处出现低谷，之后逐渐增加，在收缩段末端达到峰值，而后在直管段内逐渐趋于一个稳定值。瞬时的壁面剪切力分布如图15(b)所示，与平均值分布图不同的是在进入直管段后壁面剪切力呈现周期性波动。

图15 喷嘴上壁面剪切力分布Fig.15 The shear stress distribution on the upper wall of the nozzle

流体在刚进入收缩段时边界层受到斜面激荡而产生漩涡，导致近壁处的速度剪切变弱，进而导致壁面剪切力降低；进入收缩段后，主流场流动速度逐渐增大，边界层被压缩使得壁面速度剪切强度逐渐增大，剪切力逐渐增大；在进入直管段后速度逐步趋于稳定，且在直管段近壁处以小涡的形式出现，导致在出现小涡的位置速度剪切弱而未发生小涡的位置剪切强度较强，因此出现波动的情况。

表面摩擦系数与壁面剪切力趋势及原因亦相同，在此处不再进行赘述。

综上，喷嘴摩擦阻力系数峰值主要发生在收缩段出口处和直管段入口处，降低喷嘴流动阻力可考虑优化此处轮廓，使该处过渡更为平滑，尽可能抑制壁面边界层在该处的转捩。直管段近壁处涡结构的出现降低了摩擦阻力系数，若考虑在直管段进行减阻，可考虑被动减阻方式，使得近壁面的剪切流动变为涡流的组合，能够有效降低该段的摩擦阻力。

4 结论

本文通过采用大涡模拟模型对喷嘴内部流动情况进行描述，分析表明大涡模拟能够有效的模拟出近壁处边界层的流动状况。发现直管段近壁处出现周期性的有序涡结构，与他人数据对比证明数值模拟的有效性。同时揭示了喷嘴内近壁处的流动特性。具体结论如下：

(1)由喷嘴速度分布可知，流体在收缩段中逐渐加速，由初始的抛物线分布逐渐转变成M型分布，到直管段入口处在近壁处呈现速度峰值；

(2)喷嘴收缩段入口处由于近壁处流动受到收缩斜面激荡而导致边界层在该处附近发生转捩，使得边界层变为湍流；在收缩段出口处附近发生边界层转捩与分离，导致产生分离涡，且该处由于不同方向来流交汇使得湍流程度最大；之后在直管段受到约束逐渐稳定并在直管段壁面出现周期性涡结构；

(3)通过对速度剪切分布、壁面切应力分布以及表面摩擦阻力系数分布分析可以看出，摩擦阻力主要出现在收缩段出口处和直管段，且从表面摩擦阻力系数角度来看，峰值出现在直管段入口处。喷嘴减阻可以考虑优化收缩段到直管段的过渡轮廓以及在直管段壁面采用被动减阻方式；

(4)为获得流动状态更为稳定的射流结构，喷嘴内部收缩段与直管段交接处应采用良好的过渡，建议采用流线型轮廓进行过渡。