基于SVD转子不平衡不对中故障的轴心轨迹识别

肖鑫龙，杨洪涛,2，陈贺，郭晓军，钱秋蔚，顾建华

基于SVD转子不平衡不对中故障的轴心轨迹识别

肖鑫龙1，杨洪涛1,2，陈贺1，郭晓军3，钱秋蔚3，顾建华3

（1. 安徽理工大学 机械工程学院，安徽 淮南 232001；2. 安徽理工大学 矿山智能装备与技术安徽省重点实验室，安徽 淮南 232001；3. 无锡市新久扬机械制造有限公司，江苏 无锡 214181）

针对转子轴心轨迹存在噪声、共振等外部干扰问题，提出了一种基于奇异值分解（SVD）对转子信号进行降噪提纯的方法。通过采集转子轴向信号X和径向信号Y构造Hankel矩阵，对矩阵进行SVD分解，根据奇异值差分谱峰值选取有效奇异值来重构信号，将重构后信号合成轴心轨迹完成降噪提纯过程。经仿真分析，SVD能有效对信号进行降噪提纯。在转子实验中，将SVD用于转子故障轴心轨迹提纯。实验结果表明，经SVD降噪后的轴心轨迹清晰可见，转子不平衡的轴心轨迹为椭圆形，不对中的轴心轨迹为香蕉形，与理论相符。因此，SVD算法能有效提纯轴心轨迹并成功识别转子故障。

轴心轨迹；奇异值分解；转子故障；信号重构；有效奇异值

1 引言

转子作为重要的旋转机械零件，工作环境一般极为恶劣。在转子工作的过程中最容易出现转子不平衡和转子不对中故障[1]。造成转子不平衡的主要因素可以归结为安装误差、材质不均匀、受热条件不均匀和旋转过程中部分零部件磨损等；造成转子不对中的原因主要是安装误差、承载后的变形和环境温度的变化[2]。尤其是在高速旋转的过程中，如果转子设备监测维护不及时出现故障，将会对生产造成很大的经济损失，严重时还可能会威胁到工作人员生命[2]，因此，对转子设备进行故障诊断具有很高的经济价值和工业价值。目前，查找故障的主要方法有两种，一是通过直接对转子振动信号的相位、幅值进行分析，提取故障特征[3-5]，二是通过转子轴向和径向振动信号合成轴心轨迹来识别转子故障[6]。轴心轨迹是转子旋转中心轴相对于轴承座振动位移轨迹，它可以实时反映出转子的工作状态，相比于直接分析振动信号具有更强的分辨性[7]，工作人员通过轴心轨迹对应的故障特征就可以进行检测，因此被广泛应用于转子的故障诊断。但在采集转子振动信号过程中往往因为包含大量的噪声而使故障信号特征被淹没，很难通过轴心轨迹来识别出转子产生的故障。因此把噪声和干扰信号从原始信号中分离出来对转子故障轴心轨迹的识别至关重要。

现在对轴心轨迹信号进行提纯的算法很多，例如变分模态分解(Variational Modal Decomposition,VMD)[8]、主成分分析(Principal Component Analysis,PCA)[9]、经验模态分解(Empirical Modal Decomposition,EMD)[10]、小波变换(Wavelet Transform,WT)[11]、数学形态学(Mathematical Morphology,MM)[12]等。VMD算法中惩罚因子和分解层数难以选取；PCA算法在降维中丢失的非主成分可能含有重要信号信息；EMD算法会造成信号的模态混叠；WT算法中隔点采样的方式会造成信号数据量减少从而丢失关键信号，同时WT算法也需要很强的经验知识来选取小波基；MM算法的结构元素形状和大小难以选择等问题[13]。

奇异值分解(Singular Value Decomposition,SVD)是一种非线性信号滤波处理方法，非常适合应用于非平稳信号和非线性信号的特征提取。钱征文等[14]通过仿真验证奇异值分解对白噪声和色噪声有较好的降噪效果；张景润等[15]通过奇异差分谱理论清晰地对轴心轨迹进行提纯；郭明军等[16]从能量损失角度提出有效奇异值的选取方法，进一步完善了差分谱理论并对轴心轨迹降噪提纯成功。

本文针对转子的轴心轨迹存在噪声干扰难以识别的问题，将SVD算法用于转子轴心轨迹提纯。通过HD9200数据采集系统采集转子轴向信号X和径向信号Y，构造Hankel矩阵进行奇异值分解，然后选取有效的奇异值进行重构信号，最后把降噪后的信号X和信号Y合成转子轴心轨迹，完成对转子轴心轨迹的提纯和故障识别。

2 SVD降噪原理

图1为SVD降噪原理流程图，首先将采集到的转子原始信号转换为Hankel矩阵，再进行奇异值分解，然后根据奇异值差分谱选取有效奇异值重构信号，将重构后的信号合成轴心轨迹来识别转子的故障。

图1 SVD降噪流程图

2.1 Hankel矩阵的构造

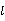
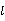
2.2 SVD分解

式（2）称为X的奇异值分解，其中：

将式（2）展开为：

将矩阵U、V写成分量组合的形式：

2.3 分量矩阵选取

上述将原始信号x构造成Hankel矩阵X，且有r个奇异值，则经奇异值分解得到各分量矩阵如下所示：

2.4 矩阵重构

则重构后的矩阵为：

3 SVD仿真信号降噪

在此信号上添加高斯白噪声，信噪比为0.5dB，得到含噪信号()。设置信号的采样率为1024Hz，采样时间为1s，采样点数为1024个。

如图2所示为原始信号的时域和频域图，时域图上信号平稳光滑，频域图上只有两个主频率。图3为含噪信号的时域图和频域图，其时域图被噪声淹没，频域图中也有很多噪声，因此，在有噪声的情况下很难有效地对信号进行分析处理。

图2 原始信号的时域和频域图

对含噪信号()按照图1流程进行SVD分解来提纯信号，如图4为奇异值和差分谱序列（取前50个），按照奇异值差分谱峰值对应序列选取奇异值，可见有效奇异值为4，因此选取前4个奇异值按式（4）进行信号重构，如图5为降噪后信号的时域图和频域图，图中信号干净平滑。选取原始信号、含噪信号和降噪信号前10个数据对比降噪效果如表1所示，在表中发现原始信号数据和降噪后信号数据一致，去除了噪声干扰。因此SVD算法能有效用于信号的提纯。

图3 含噪信号的时域和频域图

图4 奇异值和差分谱序列图

图5 降噪后时域和频域图

表1 SVD降噪前后信号数据对比

4 实验分析

4.1 实验装置

本文研究对象为如图6所示的转子实验台装置，主要由800mm*150mm的实验台体、400W伺服电机、10mm直轴钢、6200深沟球轴承、可调偏心轴承座、联轴器和负载盘组成。

图6 转子实验台装置图

4.2 轴心轨迹数据采集系统

转子轴心轨迹信号采集系统主要由HD9200数据采集器、2个WT0150电涡流传感器、HTX-V3信号调理器、转速控制箱和上位机组成，如图7所示。其中HD9200数据采集器有16个输入通道、16bit同步采样精度和最高102.4KS/s的采样频率。

图7 HD9200数据采集系统

两个相互垂直的WT0150电涡流传感器安装位置见图8，电涡流传感器的频率响应：0Khz～10Khz，灵敏度：8V/mm，数据采集系统的信号采样率：10240Hz，采样时间：0.5s，采样点数：5120个，通过采集转子的轴向位移信号X和径向位移信号Y合成轴心轨来识别转子故障。

图8 电涡流传感器安装位置

4.3 模拟转子故障及信号采集

本实验主要模拟转子不平衡和不对中故障，通过电涡流传感器采集转子轴向和径向位移信号，经SVD降噪提纯后合成轴心轨迹进行故障识别。其HD9200数据采集系统中信号的采样率：10240Hz，采样时间：0.5s，采样点数：5120个，电机转速设置：3000r/min。

实验1模拟转子不平衡故障。在同一个负载盘上分别加上1个配重螺母和2个配重螺母，如图9所示，每个配重螺母质量为5.9g。分别采集5.9g配重下转子轴向信号X1和径向信号Y1，11.8g配重下轴向信号X2和径向信号Y2。

图9 配重螺母图

实验2模拟转子不对中故障。调节可调节偏心轴承座的不对中距离为0.4mm和0.5mm如图10所示，分别采集转子0.4mm不对中轴向信号X3和径向信号Y3，0.5mm不对中轴向信号X4和径向信号Y4。

图10 可调偏心轴承座

4.4 实验处理与结果分析

对实验1中配重5.9g所采集转子的横向信号X1和径向信号Y1按照图1流程进行降噪。如图11所示，其中图c和图d分别为信号X1和信号X2的奇异值和差分谱序列（取前50个），其中信号X1和信号Y1的奇异值差分谱峰值对应序列皆为2，则按照式（4）选取前2个奇异值进行信号重构，最后将降噪后的信号合成轴心轨迹如图f所示。

图11 5.9g转子不平衡轴心轨迹图

按照图1的步骤将转子配重11.8g信号（X2，Y2）、0.4mm不对中信号（X3，Y3）、0.5mm不对中信号（X4，Y4）进行SVD降噪，最后把降噪后的信号拟合轴心轨迹，如图12、13和14所示。

文献[13]研究表明，转子系统出现不平衡故障时理论轴心轨迹为椭圆形，出现不对中故障时理论轴心轨迹为香蕉形，严重为8字形，实验结果如下。

如图11配重5.9g转子不平衡所示，原始轴心轨迹杂乱无章无法从图中识别转子故障，经SVD降噪后的轴心轨迹清晰光滑，图示为椭圆形与理论转子不平衡的故障对应。

如图12配重11.8g的转子不平衡所示，图中干扰信号基本去除。径向幅值Y2相比Y1增大约1倍，轴向幅值X2比X1约增0.5倍，且随着不平衡幅度增加，椭圆的形状越窄。

如图13转子不对中0.4mm所示，经SVD降噪后的轴心轨迹形状光滑，噪声基本去除，图中轴心轨迹为香蕉形与理论故障轴心轨迹相对应。

如图14转子不对中0.5mm所示，与0.4mm转子不对中相比较，在轴心轨迹幅值和相位上相差不大，在轴心轨迹形状上不对中幅度增大香蕉形幅度越大。

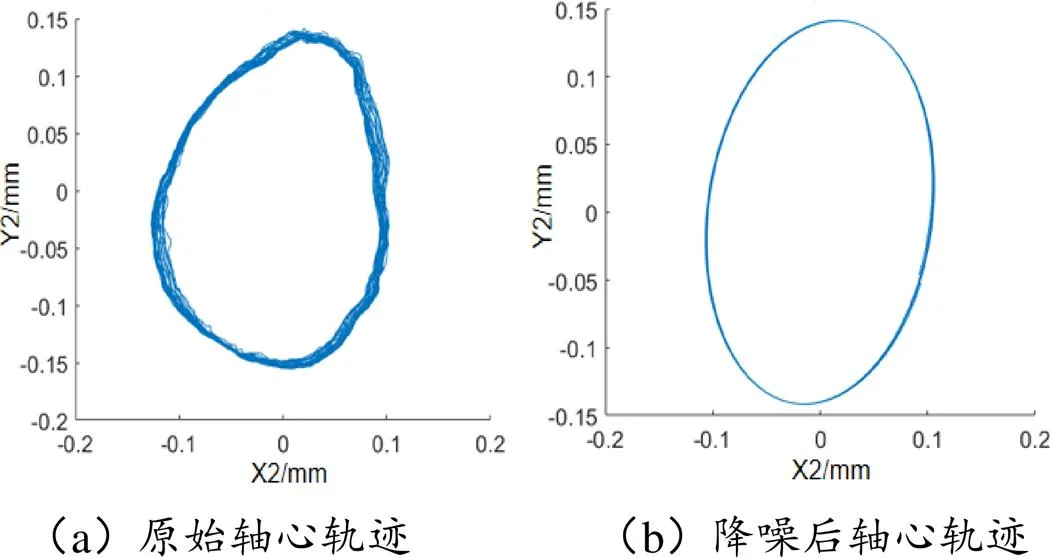
图12 11.8g转子不平衡轴心轨迹图

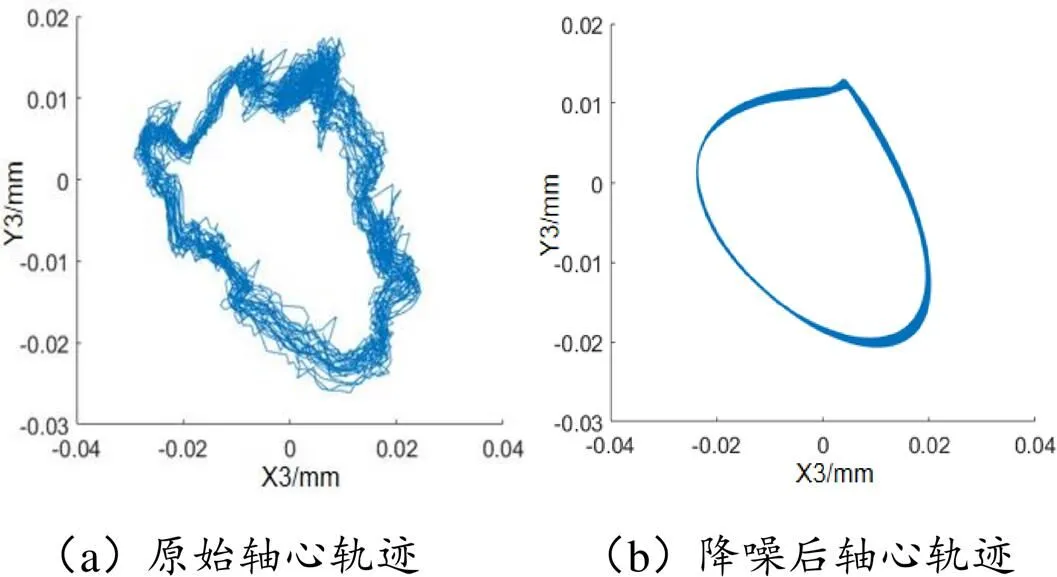
图13 0.4mm转子不对中轴心轨迹

图14 0.5mm转子不对中轴心轨迹

实验结果表明：SVD算法能有效地降噪提纯转子轴心轨迹，还能成功检测出转子不平衡和转子不对中的故障。

5 结论

本文首先通过一组正弦信号，验证SVD降噪提纯效果，然后搭建转子试验台模拟转子故障，将SVD算法用于转子轴心轨迹提纯，得到以下结论：

（1）在一组正弦信号加入高斯白噪声，进行SVD分解得到各矩阵分量，按照奇异值差分谱峰值对选取有效奇异值来进行矩阵重构并转换为一维信号，成功将噪声从含噪信号中分离出来，验证了SVD算法对信号降噪的有效性。

（2）转子不平衡实验中，经SVD算法降噪后的轴心轨迹清晰光滑，形状为椭圆形，与理论不平衡轴心轨迹一致，且随着不平衡幅度增加，椭圆的形状越窄，证明SVD算法能有效对转子轴心轨迹降噪提纯，并成功检测转子不平衡故障。

（3）在转子不对中实验中，原始轴心轨迹杂乱无章，SVD降噪后的轴心轨迹清晰可见且为香蕉形，和理论不对中轴心轨迹相符。不对中 0.5mm与0.4mm相比较，在轴心轨迹幅值和相位上相差不大，在轴心轨迹形状上，随着不对中幅度增大香蕉形的幅度也越大，验证了SVD算法能通过提纯轴心轨迹识别转子故障。

[1]李艳.转子不平衡与不对中的故障机理及其特征[J].中国石油石化,2016(S1):211.

[2]焦旭东.航空发动机振动机理和分析转子故障振动信号特征[J].粘接,2019,40(10):123–125.

[3]郭明军,李伟光,杨期江,等.稀疏表征在滑动轴承转子特征提取中的应用[J].振动·测试与诊断,2021,41(5):919–925+1033.

[4] LIU Y, ZHAO Y, LI J, et al. Feature extraction method based on NOFRFs and its application in faulty rotor system with slight misalignment[J]. Nonlinear Dynamics, 2020, 99(2): 1763–1777.

[5] LIU S, TIAN M, YANG Z, et al. The study of rotor fault feature recognition based on EEMD-ICA denoising method[J]. IOP Conference Series Materials Science and Engineering, 2018, 392.

[6] ZHENG B H , XIA L Y, GE D J, et al. Non-Stationary signal purification and rotor axis orbit feature extraction under machine tool spindle cutting process[J]. Applied mechanics and materials, 2017,4529.

[7] 程珩, 杜岚松. 旋转机械轴心轨迹故障诊断[J]. 太原理工大学学报, 2003(5): 552–554.

[8] 骆东松, 张双贵. 参数优化VMD对引风机振动信号处理研究[J]. 舰船电子工程, 2022, 42(3): 193–196.

[9]李振,李伟光,赵学智,等.基于主成分分析的特征频率提取算法及应用[J].振动·测试与诊断,2018,38(4):834–842+879.

[10]籍永建,王红军.基于EMD的主轴振动信号去噪方法研究[J].组合机床与自动化加工技术,2015(5):35–37.

[11]籍永建,王红军,孟哲,等.基于小波去噪算法的主轴轴心轨迹提纯研究[J].制造业自动化,2014,36(18):44–45+58.

[12]安连锁,胡爱军,唐贵基,等.采用数学形态滤波器的轴心轨迹提纯[J].动力工程,2005(4):550–553+586.

[13]孙慧芳,潘罗平,张飞,等.旋转机械轴心轨迹识别方法综述[J].中国水利水电科学研究院学报,2014,12(1):86–92.

[14]钱征文,程礼,李应红.利用奇异值分解的信号降噪方法[J].振动·测试与诊断,2011,31(4):459–463+534–535.

[15]张景润,李伟光,李振,等.基于奇异值差分谱理论的大型转子轴心轨迹提纯[J].振动与冲击,2019,38(4):199–205.

[16]郭明军,李伟光,杨期江,等.基于有效奇异值数量规律的滑动轴承转子轴心轨迹提纯研究[J].振动与冲击,2019,38(22):155–161.

Axis Trajectory Identification Based on SVD Rotor Unbalance Misalignment Fault

XIAO Xin-long1, YANG Hong-tao1.2, CHEN He1, GUO Xiao-jun3, QIAN Qiu-wei3, GU Jian-hua3

(1. School of Mechanical Engineering, Anhui University of Science and Technology, Anhui 232001; 2. Anhui Provincial Key Laboratory of Mine Intelligent Equipment and Technology, Anhui University of Science and Technology, Huainan Anhui 232001; 3.Wuxi Xinjiuyang Machinery Manufacturing Co., Ltd., Wuxi Jiangsu 214181, China)

Aiming at the external interference problems such as noise and resonance in the rotor axis trajectory, a noise reduction and purification method based on SVD（Singular Value Decomposition）is proposed. By acquiring the rotor axial signal X and radial signal Y, the Hankel matrix is constructed, the matrix is SVD decomposed, the effective singular value is selected to reconstruct the signal according to the peak of the singular value difference spectrum, and the reconstructed signal is synthesized into an axis trajectory to complete the noise reduction and purification process. After simulation analysis, SVD can effectively purify the signal for noise reduction. In rotor experiments, SVD is used for rotor fault axial trajectory purification. Experimental results show that the axis trajectory after SVD noise reduction is clearly visible, the axis trajectory of rotor imbalance is elliptical, and the misaligned axis trajectory is banana-shaped, which is consistent with the theory. Therefore, the SVD algorithm can effectively purify the axis trajectory and successfully identify rotor faults.

pivot trajectory; singular value decomposition; rotor failure; signal reconstruction; effective singular value

2022-03-15

安徽理工大学引进人才科研启动基金项目（2021yjrc32）；安徽省高校学科拔尖人才学术资助项目（gxbjZD2021049）

肖鑫龙（1997—），男，安徽宿州人，硕士研究生，研究方向：旋转机械故障诊断研究。

杨洪涛（1972—），男，福建莆田人，教授，博士，研究方向：仪器精度理论及应用；E-mail: lloid@163.com。

A

2095-9249（2022）03-0025-07

〔责任编校：吴侃民〕